船舶非航道航行避碰时机研究
秦 可 肖亮希 刘剑平
(1.东海海巡执法总队,上海 200000;2.洋山港海事局,上海 200000)
0 引 言
国际海上避碰规则第八条(避免碰撞的行动)各款规定了船舶在任何能见度情况下行动规则,但无论是第1、2、4款,对船舶避免碰撞的行动仅仅提供了原则性的规定,船舶驾驶人员无法根据规则确定具体的避碰时机。船舶避碰时机受多种因素影响,随当时具体环境而变,规则不可能给出确定、具体的避碰行动方法与方案,也不可能给出具体的量化规定[1]。
航海界专家学者从不同的研究角度确认船舶避碰决策模型。郑忠义教授和吴兆麟教授[2]通过对我国船长及驾驶员进行问卷调查,利用统计分析方法得到采取避碰行动可能性模糊函数,由此确认了船舶采取避碰行动时两船的距离;文献[3]运用模糊推理方法综合考虑了DCPA、TCPA等因素,然后将各因素对船舶避碰危险的隶属度和影响权重带入避碰综合评价公式;李世友[4]通过机器学习实现船舶避碰决策。
由于避碰时机的决策不仅与两船的相对状态有关,还与本船的航行领域、驾驶员的水平相关[5]。本文在模糊评判的基础上加入了基于主观的船舶碰撞危险度系数,建立了确定船舶避碰行动时机的评判模型,使得评价体系与实际情况更符合。
1 问题描述
国际海上避碰规则第八条第1款要求船舶如当时环境许可,为避免碰撞所采取的行动应是积极、及早的,其中“早”便是对采取避让行动的时机提出要求。就船舶采取避让行动而言,受到当时气象、交通密度、船速、船舶本身的操纵性能及驾驶员等因素的限制,即使在航行条件良好的开阔水域,船舶避碰时机并非越早越好[6]。本文在已知来船航向、航速、方位等信息下,本船作为让路船确定一个合适的避碰时机(采取避碰行动的距离)。
2 评判矩阵的建立
综合评判是对多种影响因素和决定事物的综合分析,在综合评判问题中通常带有一定程度的模糊性,所以应用模糊数学方法最适合,模糊综合评判法与实际中人处理数据、进行决策时的思维方式非常相似,是对人脑思考过程的重现。
2.1 因素集和评判结果集
影响船舶避让时机的因素主要有:来船舷角、相对运动速度、船速比、船舶大小、航行水域状况、船舶密度和气象条件等。
设U和L是两个有限的论域:
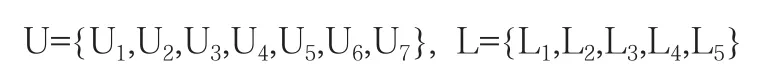
其中,U为评判因素集,即影响船舶采取最佳避碰时机的因素集,L为评判结果集,即船舶采取避碰时机可能的取值。
U的定义为:U1为相对运动速度的评判向量,U2为来船舷角的评判向量,U3为船速比的评判向量,U4为船舶密度的评判向量,U5为航行水域状况的评判向量,U6为气象条件的评判向量,U7为船舶尺度的评判向量。
L的定义为:L1=1,L2=2,L3=3,L4=4,L5=5,L的单位为海里。
2.2 建立评判矩阵
对单一评价因素Ui的评价结果可用L上的一个模糊集(Ui1/L1,Ui2/L2,Ui3/L3,Ui4/L4,Ui5/L5)表示,其中
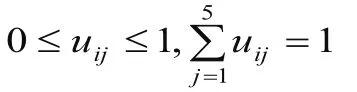
式1中i=1,2,……,7;j=1,2,……,5,得到最佳避碰时机评价矩阵E:

采用专家评判方法确定确定各评判因素集U:
U1的确定
相对速度(V01)越大避让船舶越应该提前行动,得到评价向量:
当 0 kn ≤ V01<5 kn 时,U1=(0.8,0.2,0,0,0)
当 5 kn ≤ V01<15 kn 时,U1=(0.4,0.3,0.2,0,0)
当 15 kn ≤ V01<25 kn 时,U1=(0.2,0.6,0.2,0.1,0)
当 25 kn ≤ V01<35 kn 时,U1=(0,0.2,0.6,0.2,0)
当 35 kn ≤ V01<45 kn 时,U1=(0,0,0.2,0.3,0.5)
当 45 kn ≤ V01时,U1=(0,0,0,0.2,0.8)
U2的确定
相对方位(Q)对避碰时机的影响:前方大于后方,右舷大于左舷。得到的评价向量为:
当 -10°≤ Q<10°时,U2=(0,0,0.1,0.3,0.6)
当 10°≤ Q<60°时,U2=(0.1,0.2,0.3,0.3,0.1)
当 60°≤ Q<112°时,U2=(0,1,0.2,0.4,0.2,0.1)
当 112°≤ Q<248°时,U2=(0.5,0.4,0.1,0,0)
当 248°≤ Q<270°时,U2=(0.1,0.4,0.4,0.1,0)
当 270°≤ Q<250°时,U2=(0,0.1,0.2,0.3,0.4)
U3的确定
避让时机随船速比(Kv=V0/V1)增大而延迟,根据专家打分得到船速比的评价向量:
当 Kv<0.8 时,U3=(0,0,0.1,0.3,0.6)
当 0.8 ≤ Kv<1.2 时,U3=(0,0.2,0.6,0.2,0)
当 1.2 ≤ Kv时,U3=(0.6,0.2,0.2,0,0)
U4的确定
避让时机随船舶密度(ρ)的增大而延迟,评价向量为:
当船舶密度小时,U4=(0,0.1,0.2,0.3,0.4)
当船舶密度一般时,U4=(0.1,0.2,0.4,0.2,0.1)
当船舶密度大时,U4=(0.4,0.3,0.2,0.1,0)
U5的确定
避让时机随可航水域的增大而提前,评价向量为:
在开阔水域,U5=(0,0.1,0.2,0.3,0.4)
一般水域时,U5=(0.1,0.2,0.4,0.2,0.1)
狭窄水域时,U5=(0.4,0.3,0.2,0.1,0)
U6的确定
避让时机随气象条件的变坏而提前,气象条件包括风浪及能见度情况,得到评价向量:
气象条件好时,U6=(0.4,0.3,0.2,0.1,0)
气象条件一般时,U6=(0.1,0.2,0.4,0.2,0.1)
气象条件差时,U6=(0,0.1,0.2,0.3,0.4)
U7的确定
避让时机随船舶尺度(L)的增大而提前,评价向量为:
当 L<50m 时,U7=(0.4,0.3,0.2,0.1,0)
当50m≤L<100m时,U7=(0.1,0.3,0.3,0.2,0.1)
当100m≤L<250m时,U7=(0.1,0.2,0.3,0.3,0.1)
当250m≤L时,U7=(0,0.1,0.2,0.3,0.4)
在实际避碰局面中,本船根据以上7个影响因素选取适当的评价向量,组成评价向量E。
2.3 避碰时机综合评价模型
各评判因素权重用向量X表示,X=(X1,X2,X3,X4,X5,X6,X7),在确定避碰时机中重点因素是相对方位、相对速度和船速比,根据专家评价得到各评判因素的权重:X=(0.2, 0.4, 0.15, 0.1, 0.05, 0.05, 0.05)
评价结果为:Y=X·E。在模糊矩阵复合运算中计算方式有很多种,为避免信息的丢失本文中采用加权平均型模糊算子。根据最大隶属度法反模糊化,得到避碰时机(距离)YL。
3 基于船舶主观碰撞危险度的避碰距离
为了避免以往在模糊评判中对本船操纵性、人员操纵水平的忽略,本文采取一种基于主观的船舶碰撞危险度评价模型。
3.1 船舶碰撞危险度评价模型
首先定义一个以船舶重心为圆心的船舶领域安全距离圈R,然后根据船舶操纵性能及驾驶员操纵水平来确定本船安全水域范围,一旦来船的相对运动线进入本船的安全领域即表示其对本船造成危害,随着航行环境的变化船舶安全距离圈的大小也不同[7]。
如图1所示的会遇态势下,通过AIS数据读取可以得到两船的DCPA和TCPA,考虑到DCPA和TCPA的量纲不同,采用如下方式计算本船的碰撞危险度
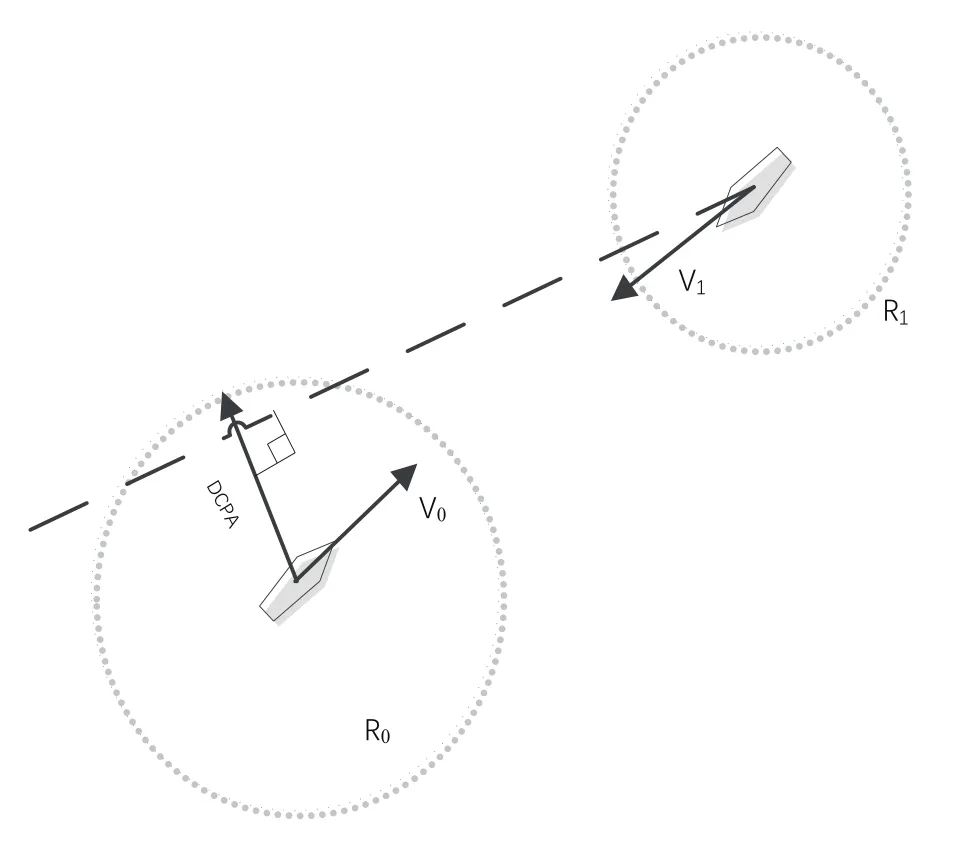
图1 船舶相对位置示意图

式中R0为本船的安全距离圈半径;T0为主观上决定采取避让措施的最晚施舵时间,两者根据船舶大小,操纵性及驾驶员的经验、操作技术等取的定值;D表示两船最近的会遇距离(DCPA);T表示两船最近的会遇时间(TCPA);当R0-D和T0-T中有一个小于或等于0时,即认为危险度为零,船舶暂且不需要采取避碰行动。对于确定的安全状态,ρ值为0,随着ρ值的增大船舶碰撞危险度增加。
3.2 避碰距离修正
根据两船避碰状态的不同修正避碰时机。
当来船相对运动线过本船重心时ρ=1,船舶最佳采取避碰时机为:l=YL
当来船相对运动线与本船的避让方向同侧形成碰撞危险时,船舶最佳采取避碰时机为:l=(2-ρ)YL
当来船相对运动线与本船的避让方向异侧形成碰撞危险时,船舶最佳采取避碰时机为:l=ρ·YL
4 算例分析
设本船的速度V0=13 kn,航向C0=0000,目标船的速度和航向为V1=19 kn,C1=2400,目标船的方位B=0320,距离D=6.0海里,本船船长L=189 m,天气良好、水域开阔、船舶密度小。
根据数据得到与目标船的相对速度V01=27.9 kn,相对方位Q=0320,船速比Kv=0.68,最近会遇距离DCPA=0.5,最近会遇时间TCPA=12.9 min。
于是得到评价矩阵E为:

将X与E带入Y=X·E式中,得到评判结果Y=(0.1,0.39,0.27,0.235,0.15),由最大隶属度原则第二种决策比较理想,即YL=2 nm。根据碰撞模型得到船舶避碰危险度ρ=0.75(R0=2 nm,T0=15 min)。
由图知来船的相对运动线与本船的避让方向同侧,所以将ρ带入l=(2-ρ)式,得到最佳采取避碰距离l=(2-0.75)*2=2.5海里。
专家评判意见为:2-3海里;2海里左右;2海里;1-3海里,2-3海里。结果表明模糊评判确定的避碰时机与专家意见基本一致,本文构造的船舶避碰时机的度量方法是可行的。
5 结 语
本文采用模糊评判对于影响船舶避碰时机的因素分析研究,并在此基础上加入了船舶主观碰撞危险度评价模型,从而建立模糊评价矩阵模型。此模型通过加入船舶主观情况,弥补了以往评价体系中仅仅考虑船舶相对的状况,使得评价模型更加贴切、合理。通过对船舶实际情况的分析计算,表明各因素对避碰时机的影响采用模糊评判方法是可行的,该模型为船舶避碰提供可量化的参考。

图2 船舶相对位置示意图

