动车组制动盘热仿真方法适用性研究

左建勇，王雪萍，周苏芬，夏铭辰

（1.同济大学 铁道与城市轨道交通研究院，上海 201804；2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804）

基础制动摩擦副是列车安全运营的重要保障，通过制动盘与制动闸片的相互摩擦作用将动能转化为热能，使列车减速或停车。制动摩擦热使制动盘的温度急剧升高，由于制动闸片摩擦块的结构及分布特点，制动盘上存在温度梯度，产生热应力［1-2］。反复制动作用导致热应力超过材料强度极限后，制动盘会发生热疲劳裂纹损伤，严重时制动盘失效，影响列车安全运行［3-4］。

针对制动盘的热生成问题，采用了数值分析、有限元仿真或模拟试验等方法开展研究。初期，得到一维和二维热传导方程［5-6］，但对于三维热传导问题，数值分析方法过于复杂。后期，随着计算机的发展，模拟试验条件受限且成本较高，通常采用有限元仿真研究制动盘热机械性能［7］，包括能量折算法、热机耦合法、热机-磨损耦合法以及流固耦合传热法等。

能量折算法是应用最广泛的列车制动盘温升研究方法，也就是假设摩擦副接触状态保持不变，摩擦副在制动过程中的相互作用被简化为输入到制动盘表面的热流量［8］。丁群、赵文清等［9-10］建立三维对称有限元模型，根据制动能量计算盘形制动产生的热流量，分析制动过程中制动盘温度场和应力场，仿真结果与试验数据比较接近。赵海燕等［11］对160 km·h-1动车组紧急制动工况下制动盘温度场瞬态特征进行研究，并探讨制动模式设置和环境因素对制动盘温度场的影响。卢术娟等［12］对制动盘进行紧急制动工况的热机械性能分析，并对制动盘散热筋的排列方式进行优化。采用能量折算法进行制动盘热仿真研究时，只需建立独立的部分制动盘模型即可，需要较少的计算资源，但却忽略了摩擦副间的相互作用。

考虑制动过程中温度场和应力场的相互作用，采用热机耦合法研究列车制动盘热机械性能。考虑制动盘的材料特性，以库仑接触摩擦热为热源，Adamowicz［13］和Yevtushenko 等［14］利用ANSYS软件对制动盘进行瞬态和接触分析，讨论接触应力对温度分布的影响。陈友飞［15］分别建立制动盘热分析模型和热力耦合分析模型，研究分析制动盘的瞬态温度场和应力场分布规律，结果表明应力场对温度场具有一定的影响，制动器主要承受热应力。李明［16］建立高速列车摩擦副热机耦合模型，分析不同制动盘材料的热物理性能参数对制动过程中温度和应力的影响，发现热机耦合数值模拟可以较好地反映制动盘盘体的温度和应力分布及变化趋势，为探讨制动盘失效机理提供参考。

另外，在热机耦合法的基础上考虑材料磨损，采用热机-磨损耦合法建立热机-磨损耦合模型分析制动盘温升规律和摩擦副接触状态。Han 等［17］通过试验发现闸片前部表面的磨损程度大于后部，基于热机-磨损耦合模型分析了不均匀接触压力与不均匀磨损之间的相关性。Wu 等［18］提出一种模拟制动盘瞬态热行为的有限元方法，研究材料磨损对材料热弹性的影响，并通过试验对模型进行优化，结果表明盘面温度分布明显受磨损的影响。

除了考虑摩擦副本身的相互作用，还考虑制动过程中空气流场对通风式制动盘散热的影响，采用流固耦合传热法研究列车制动盘热散逸规律。Bel‑hocine 等［19-20］应用有限元软件研究不同制动工况下制动盘的应力集中和结构变形，同时采用CDF分析法研究制动盘周围气流分布。对于对流换热系数和复杂流场的影响，Pevec 等［21］通过计算流体动力学，仿真通风式制动盘在不同车速和温度工况的对流传热系数，并将结果导入制动试验的数值仿真，使仿真结果更贴合试验结果。Yan 等［22］设计出一种新型制动盘结构，通过流体动力学仿真和试验，发现新型制动盘具有更好的热散逸性能。骆清国等［23］采用流体动力学和有限元方法建立压缩机的流固耦合模型，研究压气机叶轮内部流场的应力分布。

以往研究大多采用某一种仿真方法对制动盘进行热机械性能研究，未对目前普遍采用的有限元仿真方法的适用性进行研究。

在制动过程中考虑列车制动舒适性，可以通过改变制动压力的大小控制列车减速度。

本文基于实际动车组基础制动摩擦副结构，分别采用能量折算法、热机耦合法、热机-磨损耦合法和流固耦合传热法，施加运营动车组制动闸片压力工况，模拟紧急制动工况下的制动盘温升，并与相同工况下的台架制动试验结果对比，对制动盘热仿真方法进行适用性分析，为制动盘热仿真研究提供一定的参考。

1 制动盘热仿真方法

1.1 能量折算法

早期的能量折算法假设热量在摩擦面上均匀分布［24］，则在制动过程中摩擦面上各个节点的热流密度q(t)为

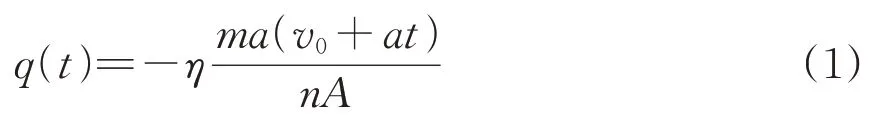
式中：η 为热量分配系数；m 为轴重；a 为列车制动过程中的减速度；v0为制动初始速度；t 为制动时间；n 为每根车轴上实际参与摩擦的制动盘摩擦面数量；A为参与摩擦的摩擦面面积。

制动盘与闸片摩擦简化示意图如图1 所示。图中：r 为制动盘上任意一点的半径；r1和r2分别为制动盘的内外半径；φ为闸片角度。

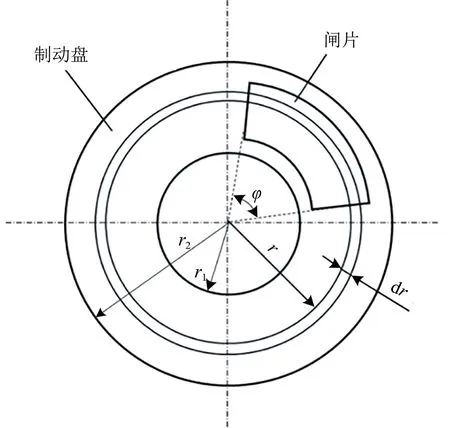
图1 制动盘与闸片摩擦简化示意图

由图1 可以看出：在实际制动过程中，闸片与制动盘沿径向接触长度不同，制动盘内外半径节点的热流密度并不相同。

因此，将闸片简化为φ弧度的空心弧扇形，并对制动盘沿径向进行环形微分，根据摩擦副在径向的摩擦接触长度计算制动盘表面的热流密度，为

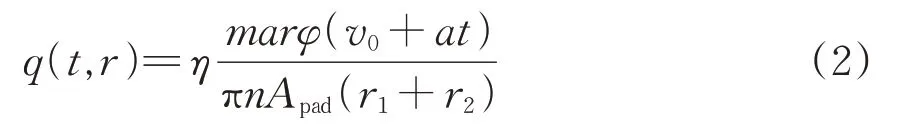
式中：Apad为闸片面积。

在进行制动盘热仿真时，为了节省仿真时间，根据制动盘循环对称的特点，选取制动盘的1/4 模型（以轴盘为例）进行仿真，如图2所示。

图2 基于能量折算法的制动盘热仿真模型

制动盘外径为640 mm，内径为350 mm，厚度为40 mm。制动盘材料为铸钢，密度为7 800 kg·m-3，弹性模量为209 GPa，泊松比为0.28，材料的热物理性能参数见表1。

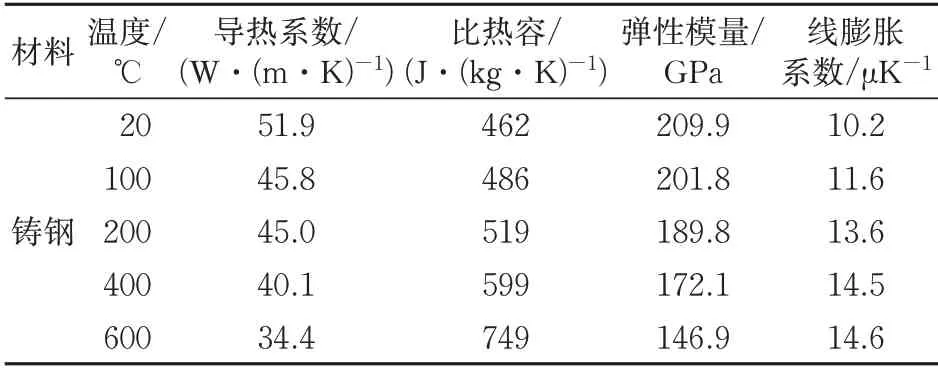
表1 制动盘材料参数

基于式（2），根据列车轴重、列车制动的初速度和制动减速度、制动盘数量及尺寸等参数计算热流密度，施加于制动盘表面。

在列车制动过程中，制动盘与周围空气域发生强制对流换热，根据经验公式［25］，对制动盘盘面、周面和散热筋结构建立不同的热对流模型，分别为

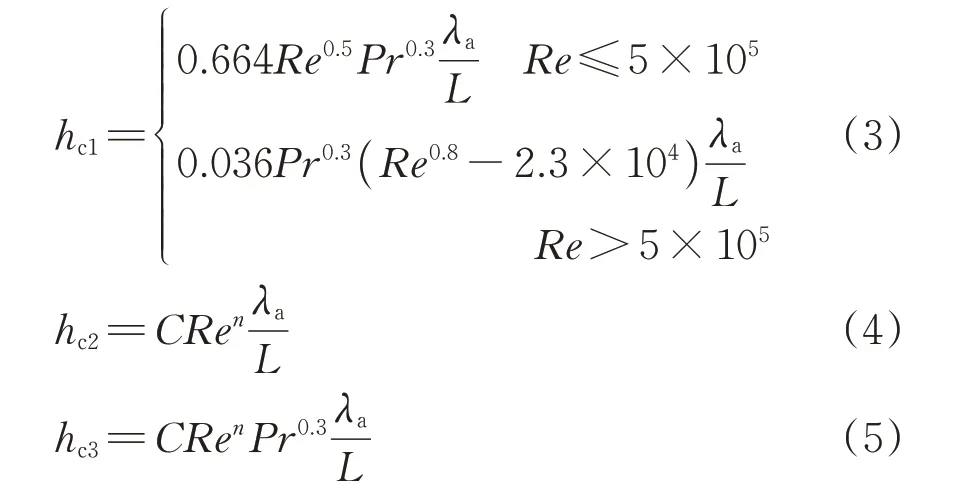
式中：hc1，hc2和hc3分别为制动盘盘面、周面和散热筋的对流换热系数；Pr为普朗特数；λa为空气的导热系数；L为特征长度；Re为雷诺数；C和n为与雷诺数相关的参数，可通过传热学表［26］得到。

1.2 热机耦合法

能量折算法忽略了摩擦副之间的相互作用，在实际制动过程中制动盘表面因不均匀温度场而产生热变形和热应力，直接影响接触状态和接触压力，接触状态和接触压力的改变反过来又将影响温度的变化，因此制动过程是一个复杂的热机耦合过程。

采用热机耦合法建立摩擦副接触模型，包括制动盘摩擦环、简化闸片摩擦块和闸片背板，如图3所示。

图3 摩擦副接触模型

制动盘摩擦副接触模型与基于能量折算法的热仿真模型尺寸相同，但简化闸片摩擦块面积为400 cm2，厚度为22 mm，闸片背板厚度为7.5 mm。制动盘和闸片背板材质为铸钢，闸片摩擦块材质为铜质粉末冶金，闸片摩擦块材料的热力学参数见表2。

表2 闸片摩擦块材料参数

在闸片摩擦块和制动盘表面设置摩擦系数为0.36；根据式（3）—式（5），分别在制动盘表面、圆周和散热筋施加对流换热系数；在制动盘底面建立对称边界条件；根据列车制动初速度和减速度计算制动盘转速，通过参考点RP 实现制动盘绕Z轴转动；根据列车轴重、制动减速度等参数计算制动压力，施加在制动闸片背板上表面，不约束闸片Z轴向平移的自由度以实现摩擦副相互接触。

1.3 热机-磨损耦合法

盘形制动过程伴随着摩擦副材料磨损行为，而磨损又会反过来改变接触面形态，影响接触压力及摩擦面温度场的分布［27］。因此，盘形制动过程伴随着温度场、应力场和材料磨损的耦合现象。

采用有限元的方法计算磨损，其核心理念就是将磨损量的计算加入有限元程序中，即在每个增量步下的热机耦合求解获取节点的温度和应力后，通过调用设定好的磨损模型计算磨损量，完成该增量步的磨损计算，再通过N个增量步的迭代完成整个磨损的有限元计算。

基于广义的Archard 磨损模型［28］计算磨损量，为

式中：W 为磨损量；K 为无量纲磨损系数；s 为滑动距离；FN为负载；H为材料硬度。

接触面积∆A中，节点的单位磨损深度∆h为

在热机耦合仿真模型的基础上，将闸片摩擦块下表面设置为材料磨损区域，通过接触节点的移动完成磨损计算。制动盘和闸片的边界条件设置与热机耦合仿真模型一致，如图4所示。

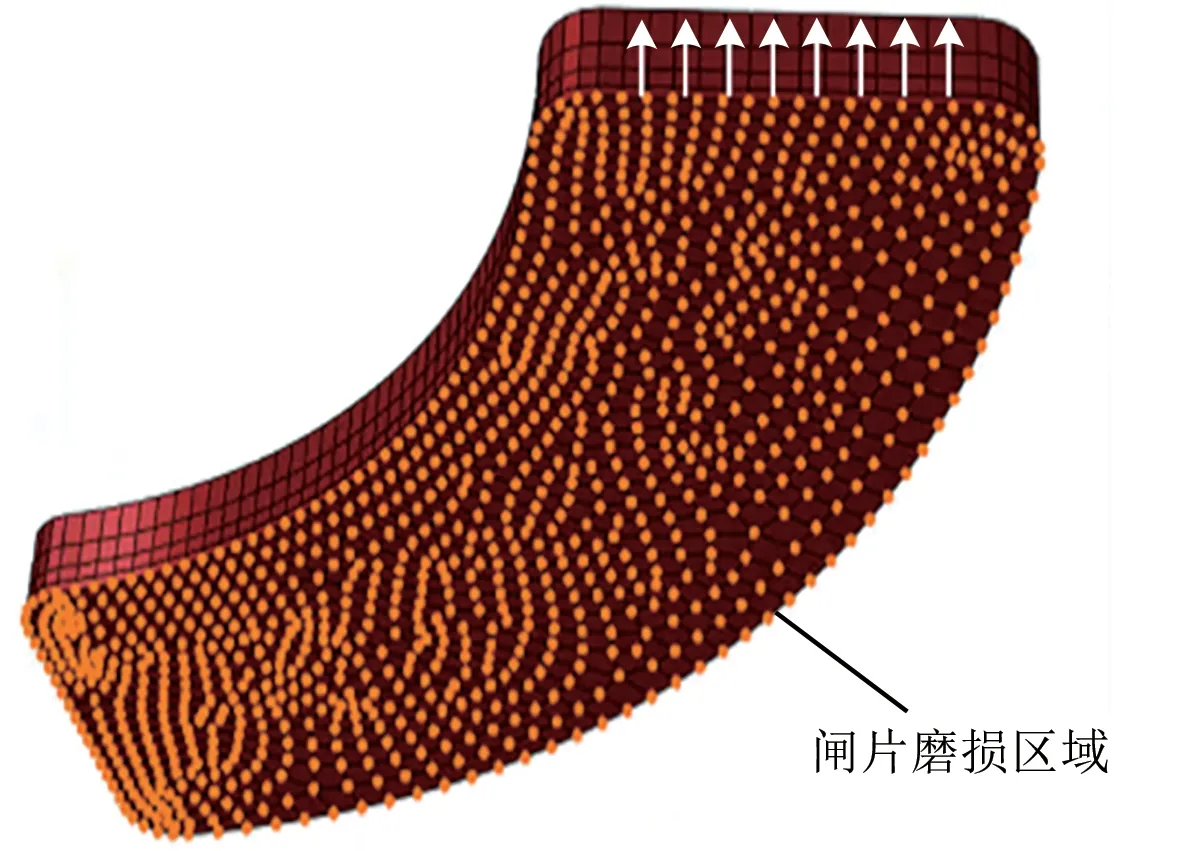
图4 闸片磨损区的边界条件设置

1.4 流固耦合传热法

采用能量折算法、热机耦合法或热机-磨损耦合法研究通风式制动盘的热传递会遇到一个共同问题，即将制动盘的对流换热系数设置为常数，但制动盘附近的空气流速会影响通风式制动盘的热散逸［29］，对流换热系数设置为常数不能体现制动盘的热散逸及其与周围空气流域的热交换。

采用流固耦合传热法，建立空气流场的流体模型和通风式制动盘的固体模型，并通过布尔运算将空气流场与制动盘模型连接起来；然后将三维实体模型网格化为非结构网格模型，导入有限元分析软件，得到具有虚拟流域的流固耦合传热模型如图5所示。

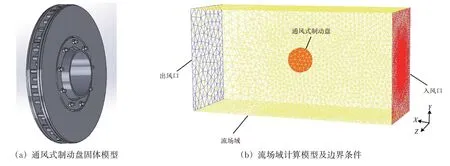
图5 基于流固耦合传热法的制动盘热仿真模型

考虑旋转效应，流固耦合模型采用RNG k-ɛ湍流模型进行求解，提高强旋转流动的计算精度。空气流场从边界面“速度入口”沿X 轴正方向进入，并以0 Pa 的压力从边界面“压力出口”流出。采用标准壁函数法对空气域壁面进行分析，其温度等于环境温度。

列车制动时，制动盘既有同列车一起前进的平移运动，同时也随着车轴做旋转运动。为了便于计算，将制动盘的平移运动转化为流体沿X轴正方向的水平运动，空气流速与列车运行速度相同；制动盘设置为绕Z轴的逆时针旋转运动，根据列车运行速度计算制动盘的旋转角速度。将空气流场和制动盘表面设置为耦合，以计算流体与固体之间的热交换。

基于能量折算法计算制动盘表面的热输入边界，通过改变流场域空气的密度、黏度和导热系数等特性模拟环境温度，仿真得到制动盘的动态对流系数。

2 台架试验

采用1∶1 制动功率试验台，以动车组铸钢制动盘和粉末冶金闸片为摩擦副，进行轴重17 t、制动初速度160 km·h-1工况的制动温升试验，施加17.5 kN（工况1）和22.5 kN（工况2）2 种制动闸片压力工况，分别对应列车减速度为1.20 和1.06 m·s-2的紧急制动工况。试验装置如图6所示。

图6 制动试验台装置

在试验过程中，制动力作用于闸片的上表面，并由压力传感器测量。埋在制动盘表面下的热电偶记录制动盘表面的温升状态，并通过红外装置对制动盘表面的温度场分布进行成像。

3 结果对比

3.1 工况1

根据制动试验工况设置仿真工况，其中：初始环境温度20 ℃，制动初速度160 km·h-1，制动闸片压力17.5 kN。该工况下基于不同热仿真方法的制动盘最高温度云图如图7所示。

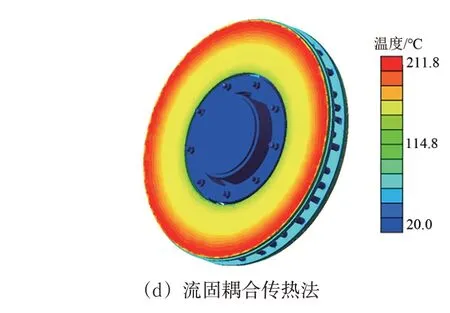
图7 基于不同热仿真方法的制动盘最高温度场分布（工况1）

由图7 可以看出：采用能量折算法、流固耦合传热法和热机耦合法进行制动盘热仿真时，由于摩擦中心线外侧节点的接触面积较大，线速度较高，制动盘表面温度为“外侧高内侧低”，制动盘高温带分布在靠近摩擦中心线外侧；当考虑闸片材料磨损时即采用热机-磨损耦合法仿真时，制动盘与闸片接触区会发生动态变化，高温带位于摩擦中心线附近。

制动试验得到的制动盘温度场分布如图8 所示。由图8可以看出：盘面有明显的高温带，分布于靠近摩擦中心线外侧，表明能量折算法、热机耦合法以及流固耦合传热法的仿真结果与试验结果比较相符。

图8 基于台架试验的制动盘最高温度场分布（工况1）

选取基于不同热仿真方法的制动盘高温带节点，其温升曲线如图9 所示。由图9 可以看出：由能量折算法和热机-磨损耦合法得到的盘面最高温度相近，分别约为220 和226 ℃；由流固耦合传热法仿真得到的盘面最高温度约211.8 ℃，基于热机耦合法仿真结果最低，约206 ℃。

图9 基于不同热仿真方法的制动盘最高温升曲线（工况1）

从计算准确角度看，4 种有限元热仿真结果基本相近，相差小于10%，属于可接受范围，因此4种热仿真方法均适用于制动盘温升研究，但热机-磨损耦合法的温度场分布与试验结果略有偏差。从计算效率角度看，能量折算法需要的参数信息较少，仿真时长不足1 h，而其余热仿真方法的计算时长普遍超过24 h，因此在运营动车组制动闸片压力工况下可以选择能量折算法研究制动盘材料的温升极限。

3.2 工况2

根据制动试验工况设置仿真工况，为：初始环境温度20 ℃，制动初速度160 km·h-1，制动闸片压力22.5 kN。基于不同热仿真方法的制动盘最高温度云图如图10所示。

图10 基于不同热仿真方法的制动盘最高温度场分布（工况2）

由图10可以看出：由4种仿真方法得到的高制动力工况制动盘高温带分布与低压力工况基本一致，但最高温度有明显差距，其中基于能量折算法的盘面最高温度仅为312.3 ℃，热机耦合的约为304.5 ℃，流固耦合传热法的约为291.6 ℃，热机-磨损耦合法的仿真结果最高，约为380.0 ℃。

制动试验得到的制动盘温度场分布如图11 所示。由图11 可以看出：盘面高温带集中在盘面中部，与热机-磨损耦合法的仿真结果相近。这是因为随着制动闸片压力增加，摩擦副之间的摩擦力增大，制动摩擦热导致闸片材料发生明显热膨胀变形，制动压力集中作用于摩擦半径处，使盘面中部出现明显高温带。

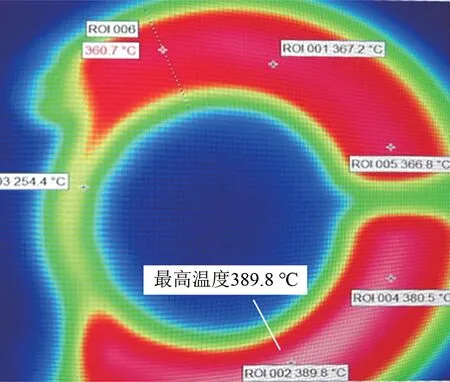
图11 基于台架试验的制动盘最高温度场分布（工况2）

选取能量折算法、热机耦合法、流固耦合传热法、热机-磨损耦合法与制动试验的制动盘高温带节点，其温升曲线如图12 所示。图中：热机-磨损耦合法为某固定节点的温升曲线，其余方法为最高温度节点的温升曲线。由图12 可以看出，当制动闸片压力值过大时，前3种有限元仿真方法的仿真结果偏低，与试验测得最高温度结果相差约80 ℃，而热机-磨损耦合法的仿真结果与试验结果比较接近。

图12 基于热仿真和制动试验的制动盘最高温升曲线

基于热机-磨损耦合仿真方法，在制动盘高温带区域选取3个节点，节点选取位置及其温升曲线如图13 所示。由图13 可以看出：盘面最高温度的位置是动态变化的，因为制动盘与闸片的接触区域是动态变化的，盘面最高温升趋势与台架试验温升曲线基本一致。

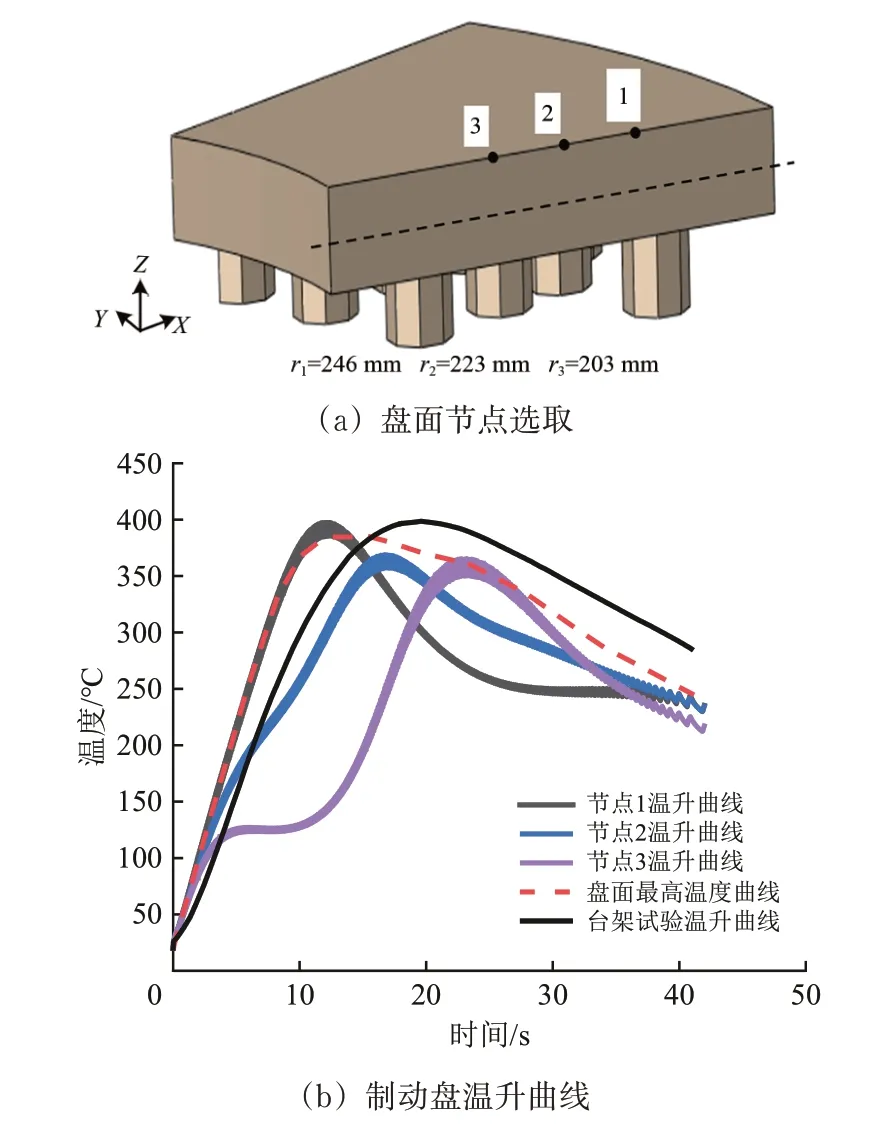
图13 热机磨损耦合法热仿真和制动试验结果对比

4 结 语

针对不同的制动闸片压力工况，应用能量折算法、热机耦合法、热机磨损耦合法以及流固耦合传热法研究制动盘温升规律，将仿真结果与台架试验结果相对比，研究4种有限元仿真方法的适用性。

在运营动车组制动闸片压力工况下，基于不同制动盘热仿真方法的制动盘温升规律基本一致，除热机-磨损耦合法，盘面温度场分布的仿真结果与台架试验结果比较相符，其中能量折算法需要较少的计算资源，大大缩短了仿真时长，计算效率高，可用于工程应用中制动盘温升极限研究。

当制动闸片压力高于22 kN 时，基于不同制动盘热仿真方法的制动盘温升规律有明显差别，基于热机-磨损耦合法的制动盘热仿真结果比较贴合台架试验结果；由于忽略了高压力工况下摩擦副相互作用及材料热膨胀变形，假设摩擦接触面积不变的热仿真方法得到的盘面温度偏低，为制动盘表面的宏观均温，而较高制动压力工况下的制动盘温升应考虑摩擦副微观的动态接触。