基于支持向量机预测模型的高速铁路现地地震预警方法

宋晋东，朱景宝，刘艳琼，孙文韬，李水龙，曾奎原，汪云龙，姚鹍鹏，李山有

（1.中国地震局工程力学研究所 地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080；2.地震灾害防治应急管理部重点实验室，黑龙江 哈尔滨 150080；3.中国地震台网中心 测震台网部，北京 100045；4.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081；5.福建省地震局 福建地震台，福建 福州 350003；6.河南辉煌科技股份有限公司 安防产品部，河南 郑州 450012）

对于高速铁路来说，地震产生的地面裂缝、地表塌陷、桥梁毁坏、隧道塌方等现象，不但会造成线路破坏、列车停运，还会带来严重经济损失，甚至对车上旅客的生命安全造成威胁［1-2］。地震发生时，迅速、可靠的地震预警是减轻地震对高速铁路造成重大经济损失和人员伤亡的有效手段之一［3-4］。

既有的地震预警系统设置了警报阈值，当观测或预测的地震动加速度峰值（Peak Ground Acce‑leration，PGA）超过阈值时，就会及时发布报警或预警信息，以便列车采取相应的紧急处置措施。文献［5］提出了1种基于阈值的地震预警方法根据P波到达后3 s 的地震记录计算得到2 个参数特征周期τc和位移峰值Pd，分别建立τc与震级M 的线性关系τc-M 模型，以及Pd与地震动速度峰值（Peak Ground Velocity，PGV）的线性关系Pd-PGV模型，在此基础上设置2 个参数的阈值，并根据地震观测τc值和Pd值与阈值的关系发布不同等级的警报。为了提升高速铁路地震紧急处置的时效性和有效性，文献［6］借鉴这一思路，基于P 波双参数提出预测高速铁路Ⅰ级地震警报预测方法，该方法沿用τc-M 模型，将Pd-PGV模型改为P波段Pd与PGA的线性关系Pd-PGA模型，在此基础上设置2个参数在不同时间窗下M=6 级时与PGA=40 cm·s-2时的阈值，并依据地震观测τc值和Pd值与阈值的关系发布不同等级的警报。但某1 种类型的P 波特征参数包含与震级相关或与地震动峰值相关的信息较单一，导致τc-M 模型以及Pd-PGA模型存在较大的离散性［7-8］，根据τc和Pd阈值发布警报会造成一定程度的误报和漏报。同时，基于文献［6］方法计算2个参数τc与Pd的取值时，需要高速铁路沿线地震监测台站的地震记录满足一定信噪比条件，行业计划大面积布设的低成本烈度仪存在噪声水准较高的问题，对该方法的适用性研究有待进一步加强。

随着人工智能的快速发展，机器学习方法已被引入地震预警领域的震级和现地地震动预测研究中［9-11］。文献［12］基于支持向量机（Support Vector Machine，SVM）建立了高速铁路地震预警震级预测SVM-HRM（SVM-based High-speed Railway Magnitude）模型，该模型的震级预测单台实现率优于《高速铁路地震预警监测系统试验方法》要求的实现率标准。文献［13］基于神经网络NN 建立了震级预测模型，该模型在P 波到达后3 s时间窗时的震级预测误差小于单参数τc-M 模型。文献［14］基于最小二乘SVM 方法，建立了用于现地地震动速度峰值预测的LSSVM-PGV（Least Squares Support Vector Machine-based Peak Ground Velocity）模型，在P 波到达后3 s 时间窗，该模型可获得比单参数Pd-PGV模型更加准确的PGV预测结果。文献［15］基于SVM 方法建立了现地地震动预测SVM-PGA与SVM-PGV模型，其对PGA和PGV的预测结果优于单参数Pd-PGA模型和单参数Pd-PGV模型。

基于单个参数建立的τc-M 模型和Pd-PGA模型等均存在较大的离散性［7-8］，地震预警中如果仅依据这2 个模型设置阈值，会造成一定程度的误报或漏报问题。尽管前述文献均以预测结果为导向不断优化模型，但根据地震观测τc值和Pd值对比阈值的警报发布形式，仍会造成一定程度的误报和漏报。

2022年1月8日，中国青海省海北州门源县发生了6.9 级地震，震后科考调查初步判定：本次地震的发震构造是祁连山脉冷龙岭断裂带；震中附近的祁连山脉冷龙岭断裂带、托莱山断裂和肃南-祁连山断裂近10年来处于活跃期，2016年以来已先后发生2次地震，震中相距不足40 km。本次地震，共记录到496 个台站、1 488 条三分向加速度记录，其中包括495 个烈度仪和1 个固定强震台加速度记录，这为烈度仪用于高速铁路现地地震预警研究提供了数据支持。

以预测高速铁路Ⅰ级地震警报为目标，在前人工作的基础上，进一步提出基于SVM 预测模型的高速铁路现地地震预警方法。该方法针对M 和PGA这2 个参数，先利用SVM 方法明确预测模型；再设置阈值（M=6 级和PGA=40 cm·s-2）并定义4个预测等级及其与阈值间的对应关系，根据预测参数值及对比阈值的结果，发布不同等级的警报；根据地震动加速度峰值观测值与预测值的对比，定义成功报警、误报、漏报和成功不报警4 个报警动作，用于对报警性能的评价。依托2022年1月8日门源6.9 级地震获得的大量近场烈度仪加速度数据，对该方法进行离线验证，分析报警结果，探索支持向量机模型在高速铁路地震预警中的可行性。

1 方 法

单参数模型具有离散性较大的不足［7-8］，而基于多个特征参数输入的SVM 预测模型可获得更加准确的预测结果［12，15］。因此，考虑用SVM 预测模型取代τc-M模型和Pd-PGA模型。

震级越大，地震造成的破坏越大。既有研究已证实M 与震中距R 无关、地震动加速度峰值会随震中距衰减［5-6］。因此，考虑在前人成果基础上进一步将震级预测SVM-HRM 模型和现地地震动加速度峰值预测SVM-PGA模型相结合，预测得到M值和PGA值并对比阈值，进而发布不同的预测等级，并根据地震动加速度峰值观测值与预测值的对比，定义4个报警动作，用于对报警性能的评价。

1.1 SVM预测模型

SVM 主要用于复杂的多特征输入的预测和回归问题［16］，其本质是用1 个复杂的线性回归函数对训练数据集进行拟合［12］，表达式为

式中：f (x)为预测值；W 为SVM 输入的各个特征参数的权重向量；b 为截距；x 为输入特征参数组成的向量。

不同于地震预测常用的最小二乘拟合方法，SVM 主要包括3个参数，这3个参数同时也是影响SVM性能的主要因素。

（1）核参数γ，即：SVM 基于核函数将样本数据映射到高维空间；

（2）容忍误差E；

（3）惩罚参数C，即：SVM 允许一定程度的拟合误差。

以高斯核函数作为SVM 预测模型的核函数，参照文献［12］的经验计算式，可分别计算得到3个参数的取值，即

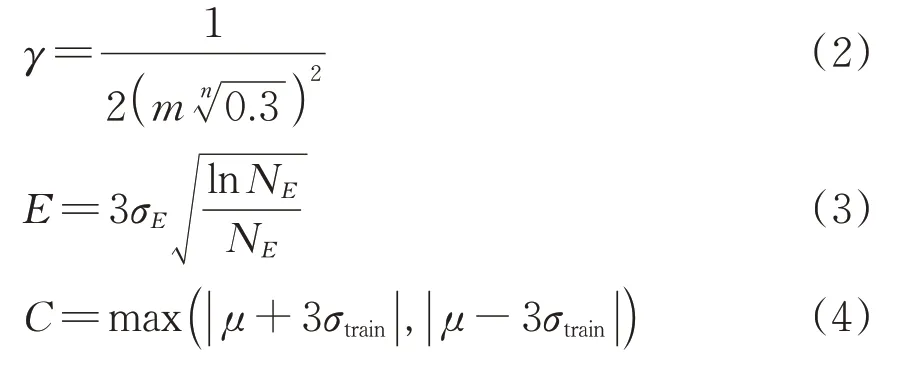
式中：n 和m 分别为SVM 输入的特征参数数量和特征参数值范围；σE为SVM 训练得到的预测值与真实值间误差的标准差；NE是SVM 训练的样本数量；μ 为SVM 训练得到预测值的平均值；σtrain为SVM训练得到预测值的标准差。

预测震级M 时，沿用文献［12］的震级预测SVM-HRM 模型，使用12 个与震级相关的特征参数作为SVM 输入，并将幅值、能量和衍生3 类特征参数统一校正到参考震源距10 km［11，17-18］。预测PGA时，参照文献［15］及式（2）—式（4）建立现地地震动加速度峰值预测SVM-PGA模型，使用10 个与PGA相关的特征参数作为SVM 输入，并将预测目标细化为0.05~5.00 Hz 带通滤波后的水平向矢量合成PGA。上述特征参数见表1。

表1 作为SVM预测模型输入的特征参数

1.2 预测等级与阈值的对应关系

我国高速铁路地震预警系统中，依据PGA大小设置了3级地震警报，由低到高分别是Ⅰ级、Ⅱ级和Ⅲ级，对应观测或预测的PGA阈值分别是40，80和120 cm·s-2［19］。针对高速铁路Ⅰ级地震警报，结合SVM 预测模型，设置2个参数的阈值分别为：M=6级和PGA=40 cm·s-2。

根据地震对高速铁路的不同影响以及高速铁路Ⅰ级地震警报的阈值，定义0~3级4个预测等级与地震动加速度峰值和震级的对应关系如图1所示。

图1 高速铁路Ⅰ级地震预测等级与阈值的对应关系

4个预测等级的含义分别是：

（1） 3 级表示大震、近震，且造成的破坏最大；

（2）2 级表示小震、近震，在台站附近区域会有一定的破坏，但造成的破坏次于3；

（3）1 级表示大震、远震，在远离台站的区域会有一定的破坏，但造成的破坏次于2；

（4）0级表示小震、远震，但不会造成破坏。

因为高速铁路发布警报时仅根据观测或预测到的PGA值与阈值的关系，不考虑预测M 值与阈值的关系，所以视PGA值超过阈值的破坏大于M 值超过阈值的破坏，即：预测2 级（PGA≥40 cm·s-2，M＜6级）的破坏大于预测1级（PGA＜40 cm·s-2，M≥6级）。

1.3 报警动作

根据图1 关系，设观测PGA为PGA，obs，预测PGA为PGA，pre，根据PGA，obs值与PGA，pre值的对比，进一步定义成功报警、误报、漏报和成功不报警4个报警动作，用于对报警性能的评价。

（1）成功报警：观测得到PGA，obs≥40 cm·s-2，预测等级是3级或2级（PGA，pre≥40 cm·s-2）；

（2）误报：观测得到PGA，obs<40 cm·s-2，预测等级是3级或2级（PGA，pre≥40 cm·s-2）；

（3）漏报：观测得到PGA，obs≥40 cm·s-2，预测等级是1级或0级（PGA，pre<40 cm·s-2）；

（4）成功不报警：当观测得到PGA，obs<40 cm·s-2，预测等级是1级或0级（PGA，pre<40 cm·s-2）。

2 验 证

2.1 地震情况

2022年1月8日，中国青海省门源县发生了6.9 级地震，震中位于北纬37.77°、东经101.26°，震源深度10 km［29］。依据中国地震局的烈度评定结果［30］，此次地震造成地表破裂约22 km，最高烈度为Ⅸ度，面积约157 km2；Ⅵ度区，Ⅶ度区和Ⅷ度区的面积分别约16 984，5 133，1 143 km2。地震发生在凌晨1时45分，因无列车在线运行且当地人烟稀少，未造成重大列车运行事故和人员伤亡。但是，这次地震对线路、桥梁、隧道和路基等高铁基础设施造成严重破坏，兰新高铁因大梁隧道坍塌以及硫磺沟大桥桥面受损而停运，带来重大的经济损失。这次地震对于硫磺沟大桥和大梁隧道的破坏情况如图2 所示，明显的结构破坏表明了本文研究的必要性。

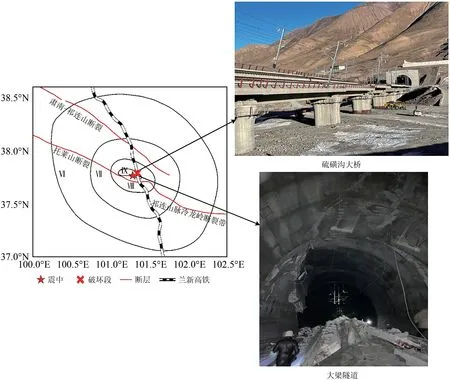
图2 门源地震烈度区以及硫磺沟大桥和大梁隧道的破坏情况

2.2 地震数据及数据处理

中国地震台网中心提供了本次地震记录到的地震数据，震中和台站分布以及中国地震局烈度评定结果如图3所示。图中：黑色实线围成的椭圆表示依据烈度评定结果［30］得到的烈度区域。在震中附近以及铁路沿线布设的台站数量众多，这为本文研究提供了数据支持。

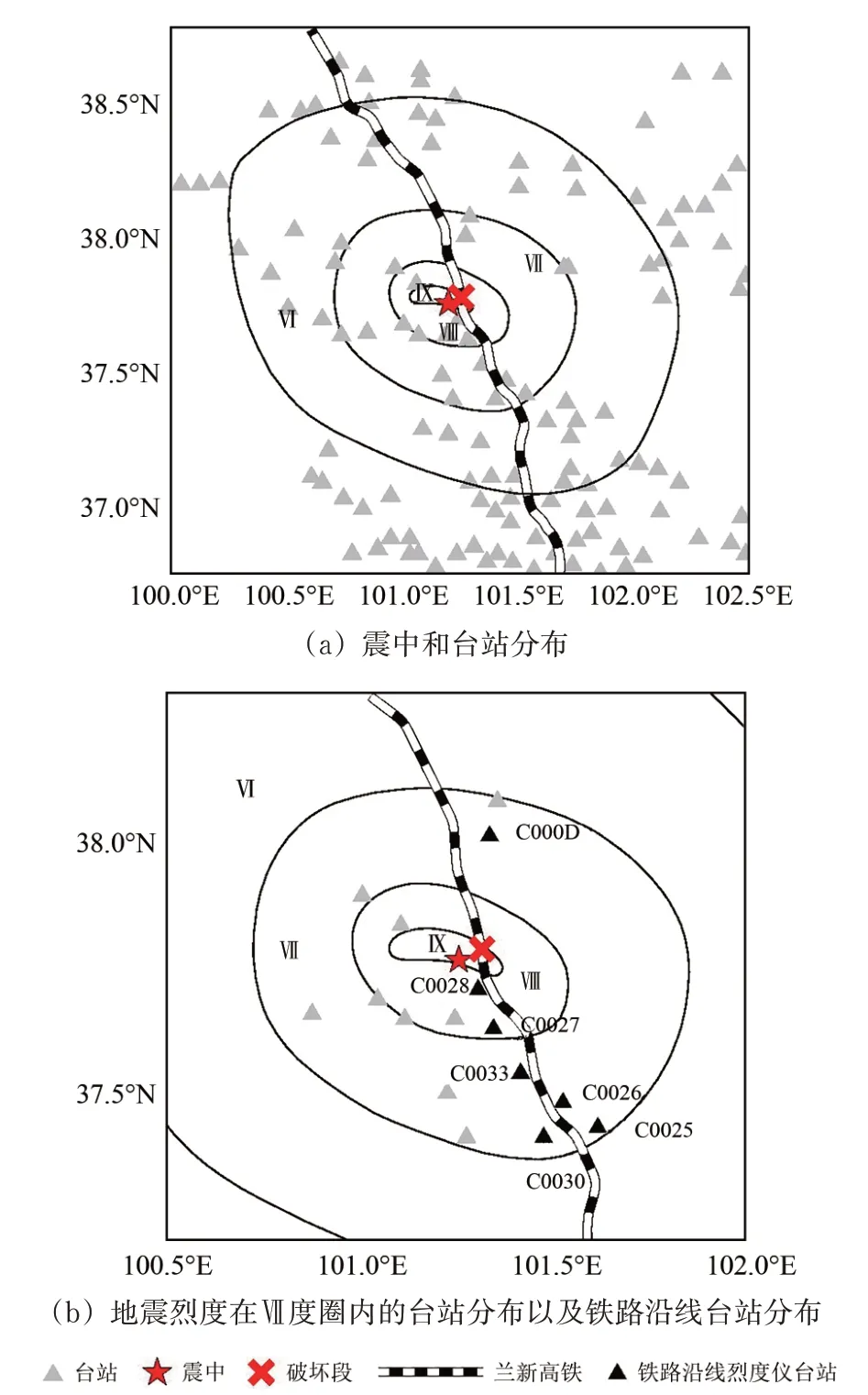
图3 2022年1月8日门源6.9级地震震中及台站分布

PGA和PGV的大小是造成地震破坏程度不同的影响因素。本次地震中，PGA和PGV与震中距R 的关系如图4 所示。从图4 中可以发现：随着震中距的增加，PGA和PGV呈现衰减趋势，这说明随着震中距的增加，地震造成的破坏在减小；在震中附近准确实现对震级和地震动的预测，对于成功发出地震预警、做好后续减灾工作而言是非常重要的。

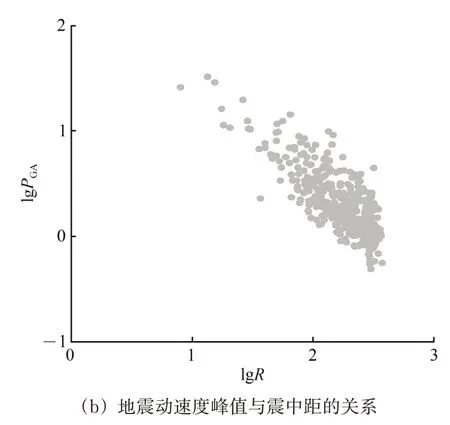
图4 门源地震的地震动峰值与震中距关系

本次地震时，距离震中最近（首台）且离破坏最近的台站编号为C0028，震中距为7.8 km。该台站记录到的PGA最大，垂直（UD）、东西（EW）和南北（NS）3 个方向的PGA分别为420.79，423.28和499.04 cm·s-2。该台站三分向加速度记录如图5 所示。限于篇幅，其他台站获取的信息不再赘述。

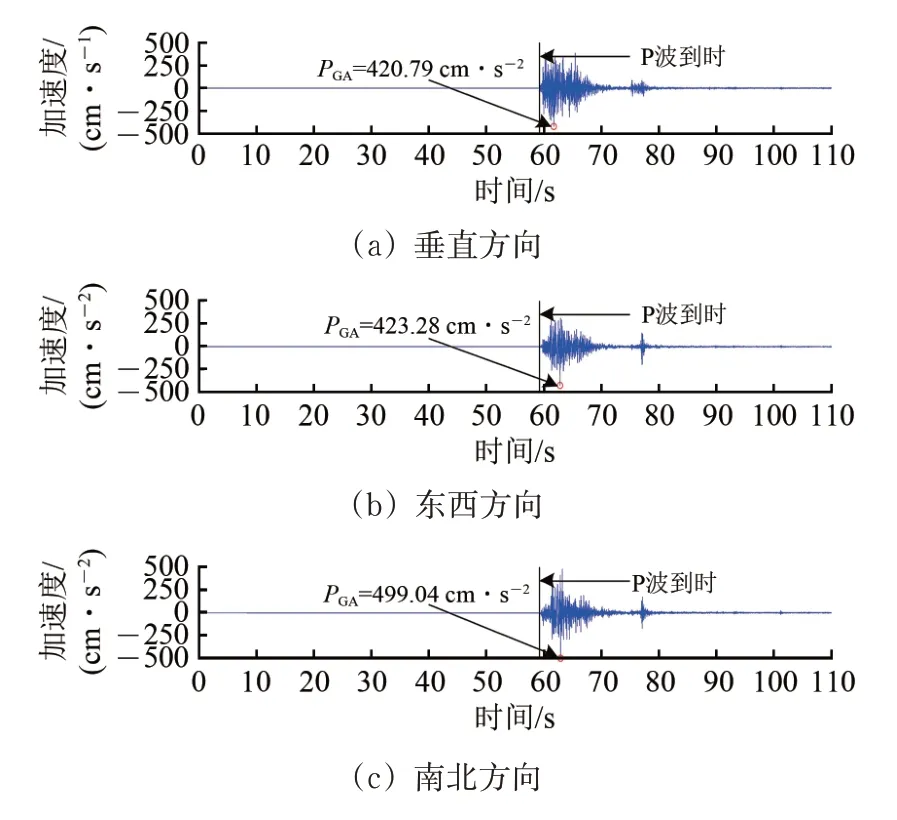
图5 门源地震中台站C0028的三分向加速度记录

为了分析阈值预警结果，对所有台站获取的全部地震数据做如下处理。

（1）对未滤波的加速度记录，采取文献［31］提出的P波捡拾方法进行P波捡拾。

（2）为消除积分造成的低频飘移［6］，对加速度记录积分一次得到速度记录，再对速度记录积分一次得到位移记录，并使用4阶0.075 Hz巴特沃斯滤波器对积分后的记录进行高通滤波。

（3）根据P波到时、加速度记录、速度记录和位移记录，计算P波到达后相应时间窗的特征参数值。

2.3 验证结果

离线验证是指地震发生后，根据台站获取的地震记录模拟实际地震发生的过程，并对所提出的方法的可行性进行验证。采用中国地震台网中心提供的全部加速度数据，对提出方法进行离线验证，先分析2 个SVM 预测模型得到的预测M 值和PGA值；再分析基于双参数预测值与阈值对比结果得到的报警结果。

2.3.1 SVM预测模型预测结果

设第i 个样本的预测震级Mpre，i的误差为ωM，i，第i 个样本的预测地震动加速度峰值PGA，pre，i的误差为ωPGA，i，则可计算得到ωM，i的平均绝对误差|ωM|和标准差σM以及ωPGA，i的平均绝对误差|ωPGA|和标准差σPGA，即

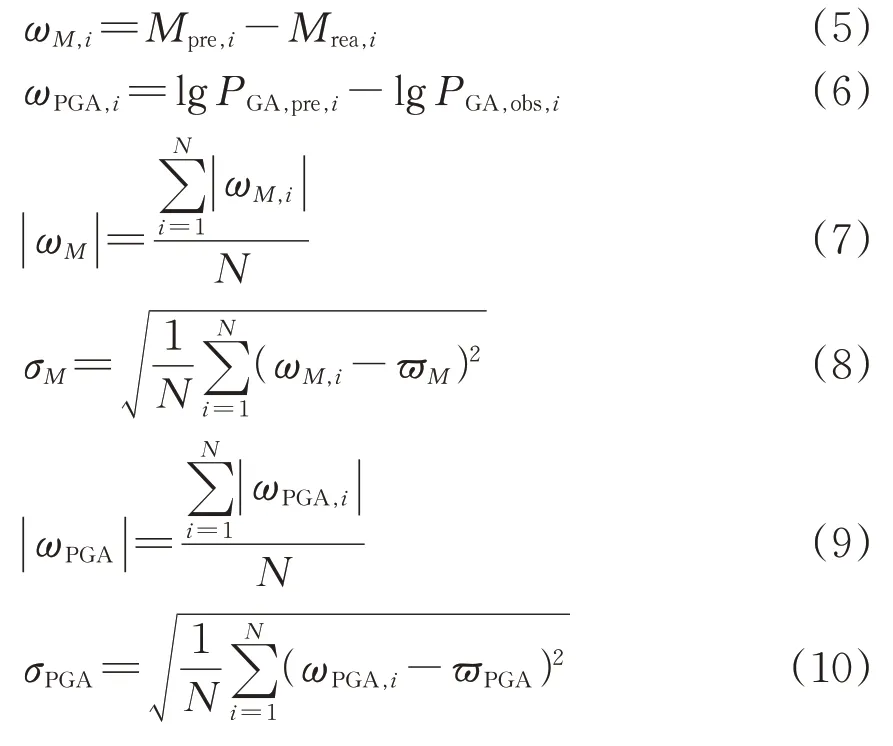
式中：Mrea，i为第i个样本的真实震级；PGA，obs，i为第i个样本的观测地震动加速度峰值；N 为总的样本量；ϖM为预测震级误差平均值；ϖPGA为预测地震动加速度峰值误差平均值。

1）SVM-HRM模型的预测结果

P波到达后时间窗分别取1，2和3 s时，SVMHRM 模型对本次地震的震级预测结果如图6所示。图中：红色、灰色实心圆分别为烈度Ⅶ度圈以内和以外台站的震级预测结果；蓝色虚线表示设置的M 阈值（M=6 级）。从图6 中可以发现：P 波到达后1 s 时，预测震级有较大的误差和离散；随着P波到达后时间窗的增加，预测震级的|ωM|值和σM值明显减小，预测震级逐渐接近实际震级；在P波到达后3 s 时，预测震级没有达到M 阈值的数量也显著减少。

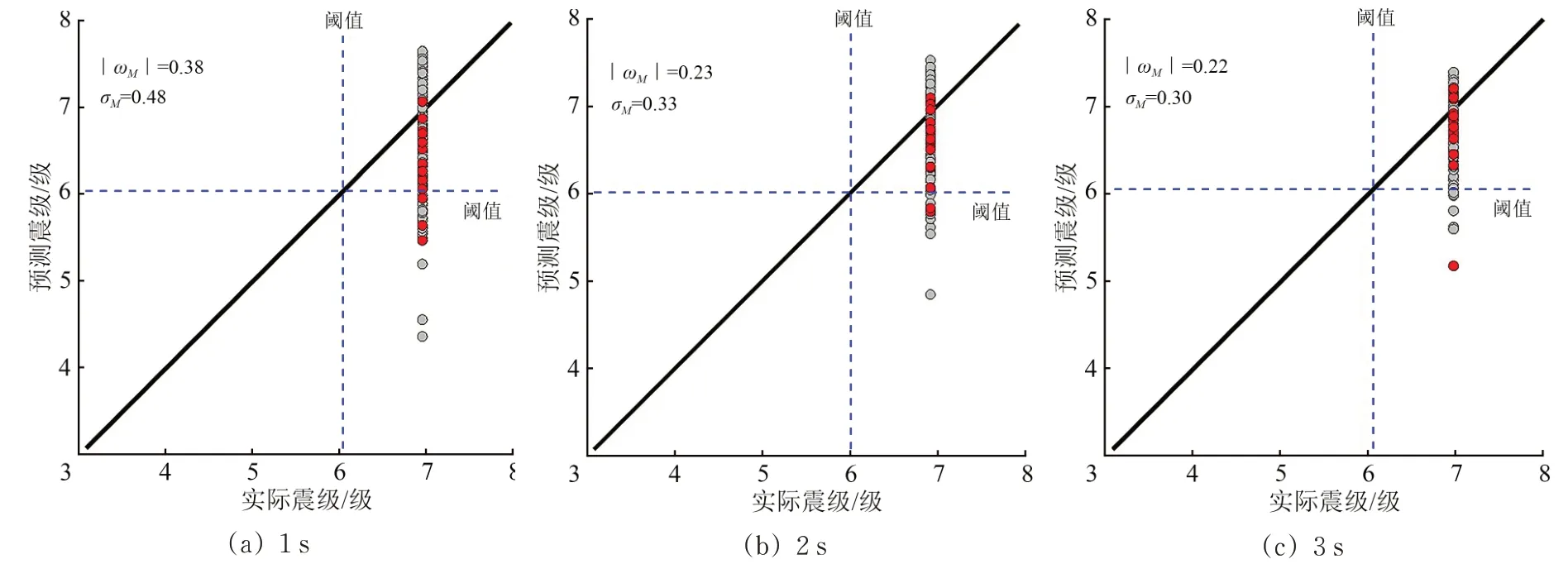
图6 基于SVM-HRM 模型的震级预测结果

P波到达后时间窗分别取1，2和3 s时，SVMHRM 模型对本次地震的预测震级误差与震中距变化关系如图7 所示。从图7 中可以发现：预测震级误差主要集中在±2σM的误差范围内，且与震中距的变化无明显关系；随着P 波到达后时间窗的增加，预测震级误差逐渐向0靠近。

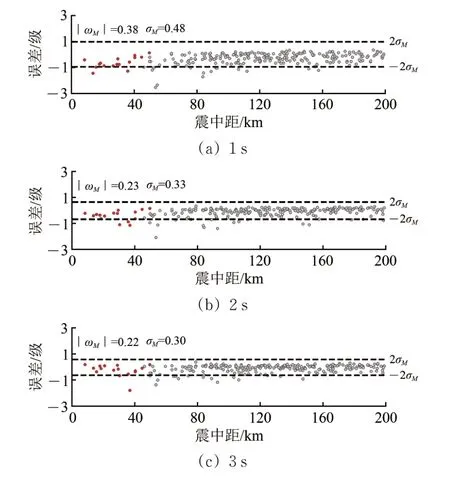
图7 基于SVM-HRM模型的预测震级误差与震中距的关系

2）SVM-PGA模型的预测结果

P波到达后时间窗分别取1，2和3 s时，SVMPGA模型对本次地震的PGA预测结果如图8所示。图中：红色、灰色实心圆分别为烈度Ⅶ度圈以内和以外台站的PGA预测结果；蓝色虚线表示设置的PGA阈值（PGA=40 cm·s-2）。从图8 中可以发现：在P 波到达后1 s 时，预测PGA值有较大的误差和离散；随着P 波到达后时间窗的增加， | ωPGA| 值几乎没有明显的变化，预测PGA的σPGA值明显减小，预测PGA值逐渐接近观测PGA值；在P 波到达后3 s时，预测PGA值没有达到PGA阈值的数量也显著减少，预测值与真实值呈现1∶1的线性关系。

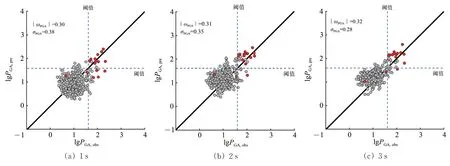
图8 SVM-PGA模型的地震动加速度峰值预测结果

P波到达后时间窗分别取1，2和3 s时，SVMPGA模型对本次地震的预测地震动加速度峰值误差与震中距变化关系如图9所示。从图9中可以发现：预测地震动加速度峰值误差主要集中在±2σPGA的误差范围内，且与震中距的变化无明显关系；随着P波到达后时间窗的增加，预测地震动加速度峰值误差逐渐向0靠近。

图9 SVM-PGA模型的预测地震动加速度峰值误差与震中距的关系

2.3.2 预警结果及评价

基于模型预测M 值和PGA值，结合预测等级与阈值的对应关系，分别取首台触发后1，2，4 和6 s 时，得到烈度Ⅶ度区内高速铁路沿线台站触发情况和预测等级发布情况分别如图10 所示。由图10 可知：首台触发后1 s 时，该台站发布预测等级3；首台触发后2 s时，台站C0027触发，并发布预测等级3，此时S 波还未到达该台站；首台触发后4 s 时，台站C0033 和台站G000D 触发，并分别发布预测等级3 和预测等级1，此时S 波还未到达这2 个台站；首台触发后6 s 时，台站C0026 和台站C0030 触发，台站C0033、台站G000D、台站C0026 和台站C0030 均发布预测等级3，此时S 波还未到达这4 个台站；随着首台触发后时间的增加，触发台站的数量也随之增加，部分台站在S波还未到达之前即可发布预测等级3。

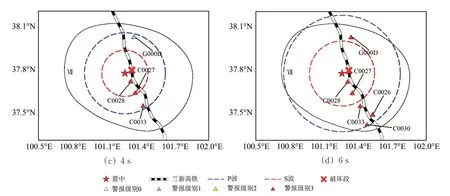
图10 Ⅶ度区内兰新高铁沿线台站触发情况和发布预测等级情况

对应图10，分别取首台触发后1，2，4 和6 s时，已触发台站的报警动作分别见表2。结合图10和表2可以发现：只有台站G000D在首台触发后4 s时发生漏报，其余情况全部台站均成功报警，且未出现误报和成功不报警的情况。

表2 Ⅶ度区内高速铁路（兰新高铁）沿线已触发台站报警动作

对唯一未能成功报警的台站G000D 进行分析，发现：在首台触发后4 s时，该台站刚刚触发1 s且地震信号中包含相关地震动加速度峰值的信息较少，所以导致台站G000D 在首台触发后4 s 时对PGA,pre低估，进而产生漏报；但在首台触发后6 s时，台站G000D 获得了3 s 的地震信号，且成功报警。此外，导致漏报的原因也可能是大地震事件在发生初期并未完全破裂，地震波所携带的信息不足，导致预测值的低估。

由于实际震级大小与震中距无关，对于M≥6级的地震事件，按照本文方法发布的预测等级只有3级或1级，若出现2级或0级，其原因可能是低估了预测震级；对于M<6 级的地震事件，按照本文方法发布的预测等级只有2 级或0 级，若出现3 级或1级，其原因可能高估了预测震级。在后续的研究中，还可考虑通过改进SVM 预测模型，进一步减小对M 和PGA这2 个参数的预测误差，或可考虑建立更优的基于深度学习的震级预测模型和现地PGA预测模型，改善本文方法的报警准确性。

3 结 论

（1）在P 波到达后1~3 s 时间窗内，随着时间窗的增加，SVM-HRM 模型预测M 时得到的σM值和SVM-PGA模型预测PGA时得到的σPGA值均明显减小，说明预测结果在逐渐接近真实值，证明了SVM 预测模型可以对震级以及现地地震动加速度峰值进行准确预测。

（2）在P 波到达后3 s 时，预测M 值和PGA值几乎都达到了阈值；预测M 时误差和预测PGA时误差均不会随震中距的变化而明显变化。

（3） 依 据SVM-HRM模型的预测M 以 及SVM-PGA模型的预测PGA，首台触发后1 s 时就可以成功发布预测等级3；首台触发后6 s 时，烈度Ⅶ度区域内的所有高速铁路沿线烈度仪台站均可以成功发布预测等级3；首台触发后2，4 和6 s 时，部分台站在S波还未到达时可以成功发布预测等级3；首台触发后1，2和6 s时，P波触发的台站全部实现成功报警。本文提出的基于SVM 预测模型的双参数高速铁路Ⅰ级地震警报预测方法在高速铁路现地地震预警中有潜在的应用前景，也可为低成本烈度仪服务于高速铁路地震监测预警提供参考。