摩擦副摩擦半径计算之有限分割法研究
徐熙庆,肖广文,刘 壮
(克诺尔车辆设备(苏州)有限公司,江苏 苏州 215151)
0 引言
盘式制动因为具有稳定性高、承载能力强等优点,广泛应用于汽车、轨道车辆、飞机等交通工具。盘式制动的摩擦副一般由相互摩擦的制动闸片和制动盘组成,其作用是将车辆的动能通过摩擦转化为热量,实现车辆制动。在轨道车辆制动系统设计时,摩擦半径为制动闸片在制动盘上的理论施力半径,是制动计算的重要输入参数之一,该参数的准确性是十分重要的。
目前轨道车辆制动系统的测试标准有EN15328[1]及UIC541-3[2],基于环形摩擦假设,摩擦半径简化为:
式中:ro为制动盘和制动闸片接触区域外侧半径,ri为接触区域内侧半径。
因摩擦半径与产品应用相关,目前公开的研究较少。张辉等[3]基于CATIA二次开发功能,实现了基于制动闸片形状的摩擦半径计算。
上述第一种的计算方法未考虑制动闸片形状和接触面的压力分布,而张辉采用的方法未考虑接触面的压力分布,其计算结果与实际值存在偏差。
VBA(Visual Basic for Applications)是微软公司推出的Visual Basic的一种宏语言。基于Excel的VBA功能,可以将复杂的计算过程程序化,并将结果可视化,已经广泛应用于科研教育机构及企业中[4-7]。在一些机械设计软件中,如AutoCAD等,VBA也被作为进行二次开发的工具,实现定制功能和复杂计算[8-10]。
为了实现考虑制动闸片的实际形状及接触面压力分布的摩擦半径计算,基于Excel的VBA二次开发功能及有限分割法编写了计算工具,该工具实现三维建模软件中制动闸片形状数据的导入、压力分布和摩擦半径的计算。该工具可在所有安装Excel的电脑上运行,具有便捷易用等特点。程序界面见图1。

图1 程序界面
1 制动闸片数据模型
现有的三维建模软件,如Creo、Solidworks等,均可以将模型数据转化为交换格式,如stp,igs等,以实现在不同软件中的数据交互。
该工具使用igs格式数据,数据格式规范见GB/T 14213[11]。首先在三维建模软件中建立闸片形状的草绘(可由三维模型生成),导出为igs格式。
制动闸片接触面形状一般由圆弧和直线组成(少部分闸片可能包含二次曲线,但可以由多段直线或圆弧拟合)。直线和圆弧在igs的代码分别为110和102。直线数据包含起点和终点的坐标,圆弧包含圆心、起点和终点的坐标。组合曲线(代码112)是由直线、圆弧等连接起来的有序表,在制动闸片中代表了一条封闭几何,如一个由多个粒子组成的制动闸片,每个粒子的外形草绘即为一条组合曲线。一般圆弧线条使用了变换矩阵(124),需要根据矩阵变换来计算最终坐标(详见GB/T 14213中第3.14节变换矩阵实体)。
通过Excel的VBA的文本读取功能读取上述数据,并把相应的数据(直线包含起点和终点坐标,圆弧包含圆心、起点和终点坐标)保存至Excel中,当后面需要使用该数据时可以直接读取,避免重复导入。
为实现制动闸片形状的快速预览及检查,通过VBA将制动闸片1数据绘成图表,如图2所示(图中制动闸片1为了展示效果进行了特殊处理,非实际应用产品)。
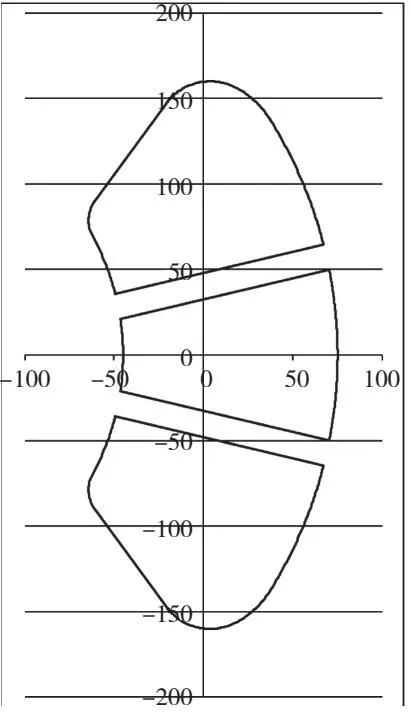
图2 制动闸片数值模型
下面使用的制动闸片2为2010版UIC541-3[12]中列出的一种粉末冶金型制动闸片。
2 制动闸片接触压力计算模型
2.1 计算模型
为避免制动盘与闸片不平行导致局部压力过大,轨道车辆的制动闸片一般可以绕制动闸片竖直方向(y向)的转轴转动。为了进行接触压力计算,基于摩擦材料弹性变形理论,进行以下设定:
1)在x坐标相同时,在y方向各处压力相同;
2)假设闸片变形为线性,则在x方向压力为线性,其线性系数为k;
3)在转轴处压力值为1。
基于以上设定,可以得到接触压力为:
q(x,y)=k·x+1
因导入的制动闸片外形转轴中心为x=0,根据两侧力矩平衡,可得
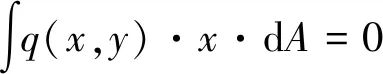
代入接触压力公式
lx为横坐标为x时闸片的有效长度(图3),将在2.2中求解,可得
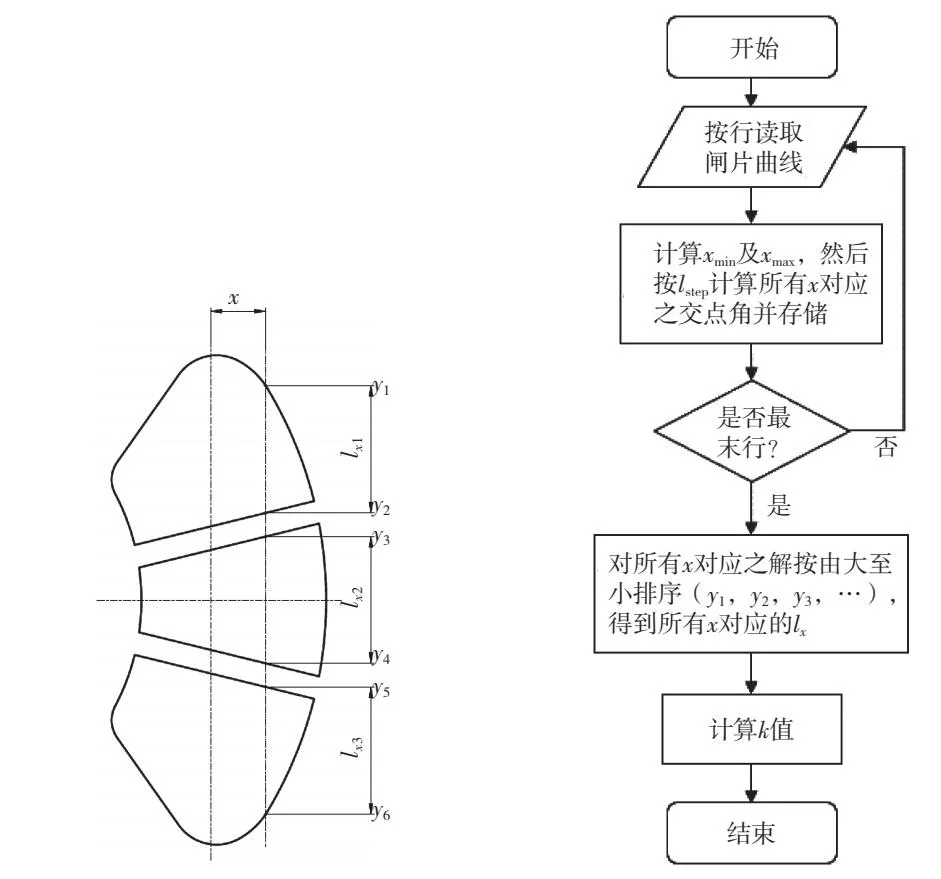
图3 制动闸片垂向有效长度图4 k值计算流程图
因制动闸片的形状较为复杂,上式积分难以求解。可以将制动闸片形状沿x方向进行水平分割(程序的分割间距为lstep=0.05 mm),可以用求和的方法来代替积分,即
上式中,∑步距为lstep,此时只需获得lx即可求得k值。
2.2 制动闸片水平分割
如图3所示,制动闸片水平分割的垂向有效长度lx为
lx=lx1+lx2+…
=y1-y2+y3-y4+…
式中,lx1,lx2……为闸片各分段长度,y1,y2……为横坐标为x处对应制动闸片线条上的y坐标。可根据下式求得线段的y坐标
可根据下式求得圆弧段的y坐标
因圆弧的y值有2个解,需要额外处理以去除无效解(根据圆弧段的起点及终点位置来判断解是否在起点和终点之间)。
为了提高求解效率,先求解单条线条的最小x值xmin及最大x值xmax,然后在该范围内根据步长lstep逐个进行y值求解,然后再处理下条线条。直到所有线条都求解后,对每一x值得到y值进行由大到小排序,最后根据本节开始时的公式对lx求解。
主要计算流程见图4。
3 摩擦半径计算模型
3.1 计算模型
制动闸片安装后,制动闸片转轴中心与制动盘旋转中心的距离为安装距离(E),如图5所示

图5 摩擦半径计算流程图
摩擦半径计算公式为
式中,r(x,y)为坐标(x,y)与原点的距离,A为制动闸片接触面的形状面积。
因安装后制动闸片中心的x=E,式中
q(x,y)=k·(x-E)+1
式中
x=R·cosα
dA=R·Rstep·dα
式中,α为坐标(x,y)相对原点的角度(x轴上方为正值,下方为负值)。
摩擦半径计算公式可转化为
因制动闸片的形状较为复杂,上式积分难以求解。可以将制动闸片形状在以制动盘中心为圆点进行径向分割(如Rstep=0.05 mm,见图5),可以用求和的方法来代替积分,即

式中,∑步距为Rstep,此时只需获得αx(α1,α2,…)即可求得rm值。
3.2 制动闸片径向分割
类似于2.2节水平分割的计算模型,可以通过建立径向分割的计算模型,求解半径为R时的所有分割角度值。同样的,在求解过程中存在2个解的情况,需要额外处理以去除无效解(根据圆弧段的起点及终点位置来判断解是否在起点和终点之间)。
为了提高求解效率,先求解单条线条的最小R值Rmin及最大R值Rmax,并在该范围内根据步长Rstep逐个进行α值求解,然后再求下条线条。直到所有线条都求解后,对每一R值得到α值进行由大到小排序,最后再根据3.1节中的计算公式进行rm求解。
主要计算流程见图6。
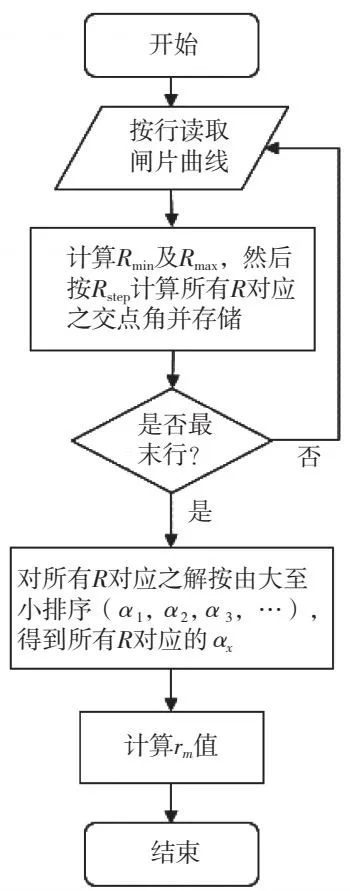
图6 制动闸片垂向有效长度
4 计算结果分析
4.1 计算结果对比
以文中制动闸片1为例,在安装距离E为230mm时(适于摩擦面外径为640mm,内径为350mm的制动盘),通过程序计算出摩擦半径为245.1mm。在表1中称为方法1。
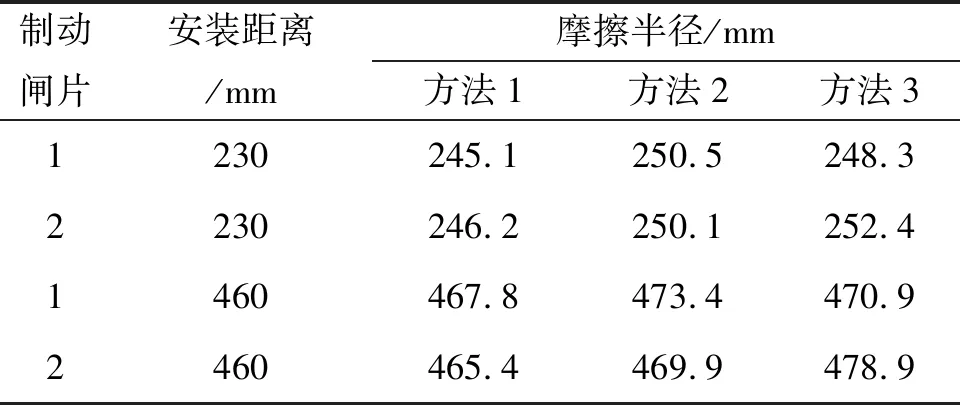
表1 摩擦半径计算结果
程序同时可计算出不考虑制动闸片压力情况下的摩擦半径(该情况不需要进行接触压力计算,在摩擦半径计算过程中k定义为0,适用于制动闸片完全约束的情况)。在表1中称为方法2。
程序计算出相同安装参数制动闸片1与制动盘接触区域外侧半径和内侧半径分别为304.5 mm和181.7 mm,根据第1节中的公式计算得摩擦半径为248.3 mm。在表1中称为方法3。
类似的计算出相同安装参数下制动闸片2的摩擦半径。
为了对比,计算出2种制动闸片在安装距离E为460 mm(适于摩擦面外径为1085 mm,内径为805 mm的制动盘)时的摩擦半径。
程序可以通过Excel的图表功能直接将计算结果展示出来,2种闸片在安装距离为230 mm的计算结果图示见图7。

图7 制动闸片1及制动闸片2计算结果图示
从表中数据可以得出:
1)不考虑制动闸片形状(方法3)得到的摩擦半径与理论值(方法1)存在一定偏差,在制动闸片非扇形结构情况下,可能会造成更大的偏差;
2)不考虑制动闸片压力(方法2)得到的摩擦半径与理论值存在一定偏差;
3)制动盘尺寸不一样也会导致偏差不同,偏差的大小与制动闸片的实际结构形状有关。
4.2 不同安装距离摩擦半径对比
通过程序对制动闸片1在安装距离从150 mm 至350 mm的摩擦半径进行计算(间隔20 mm),结果见表2。
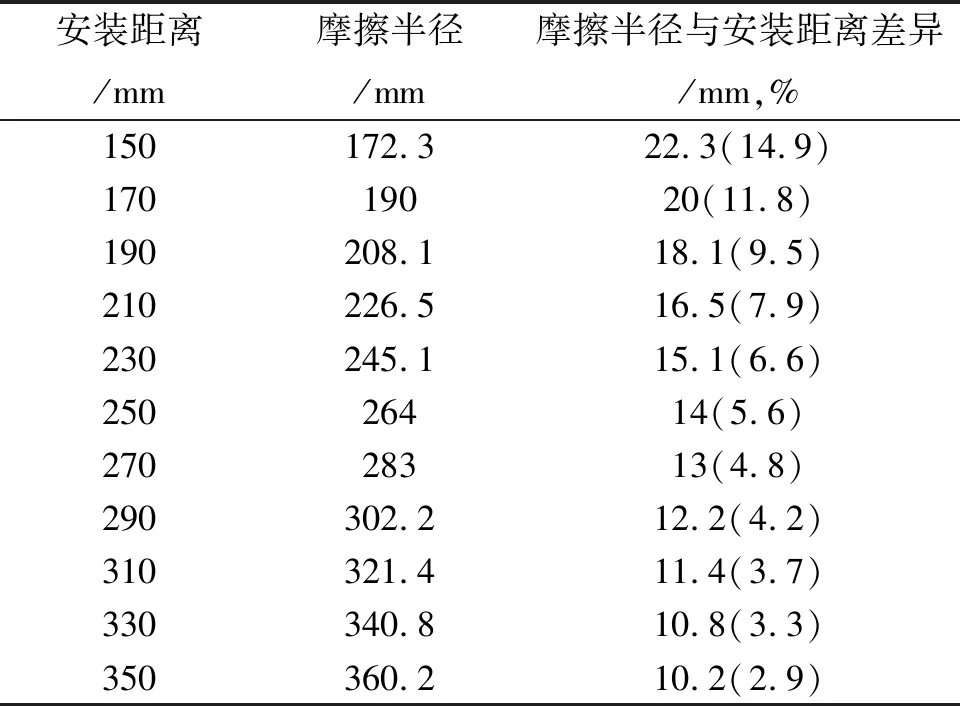
表2 不同安装距离摩擦半径对比
从表中数据可以看出,摩擦半径随着安装距离的变化呈非线性变化,在实际应用中需要根据具体安装距离进行计算。
4.3 制动盘和制动闸片相对位移对摩擦半径的影响
因制动盘和制动闸片安装在轨道车辆的不同位置,在实际运营过程中因车辆振动、载重影响,会造成制动盘和制动闸片的相对位置与初设位置不同。X方向的相对位移会直接导致安装距离E的变化,从而引起摩擦半径的相应变化,可以通过程序进行计算(因变化范围相对E的比例较小,可近似假设安装距离E的变化与摩擦半径的变化相同)。
通过程序可以计算Y方向的相对位移,从0 mm 至30 mm,间隔为 10 mm变化时对应的摩擦半径,以制动闸片1为例,在安装距离为230 mm时的计算结果见表3。
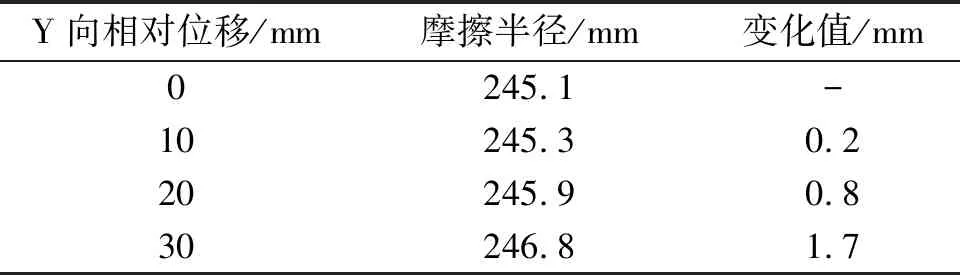
表3 不同Y向位移的摩擦半径对比
通过表中数据可以看出,Y方向的相对位移对摩擦半径的影响较小,在实际应用中可以忽略。
5 结论
本文介绍了一种通过Excel的二次开发功能编写的摩擦半径计算程序。通过该程序,可以实现不同安装参数下制动闸片摩擦半径的快速计算,并以图示的形式展示,可用于制动闸片的产品开发及产品应用的计算。
通过对程序的计算结果进行相关分析,得出如下结论:
1)计算摩擦半径时假设制动闸片为与制动盘同心的扇形或圆环形,以及不考虑制动闸片的压力分布,可能造成结果与理论摩擦半径相差较大,产品应用时应根据制动闸片的结构及压力分布进行计算;
2)安装距离的变化会造成摩擦半径的非线性变化,实际应用中需要根据相应的安装参数进行计算;
3)制动盘和制动闸片相对位移会导致摩擦半径的变化。X方向的相对位移对摩擦半径的影响可以通过变化后的安装距离E进行计算。Y方向的相对位移对摩擦半径的影响较小,在实际应用中可以忽略。

