一种削弱积分型滑模结构的永磁同步电机矢量控制系统

沈 维, 孙 磊, 司宾强, 张 军

(1.盐城工学院 机械工程学院，江苏 盐城 224051；2.北京信息科技大学 自动化学院，北京 100096)

0 引 言

传动系统已广泛应用于工业生产,随着电力电子科学技术、操控理论研究及其微电子技术的发展,交流永磁同步电机(PMSM)凭借其优越的控制性能，广泛用于高精密数控机床、激光切割、纺织等对系统精度和可靠性要求严格的领域[1]。然而PMSM是一个复杂非线性系统，在实际运行中无法忽略电机参数随运行环境的变化，从而影响控制器的调节性能。关于此现象,国内外研究者提供了多种优秀的先进算法以提高PMSM的调节特性,包括PID调节[2]、模糊控制[3]、自适应控制[4]以及滑模控制(SMC)[5]等。

基于SMC的PMSM控制系统实质上是一个非线性控制系统,与常规控制策略不同在于,其控制过程是不连续的,通过根据控制系统当前状态不断切换起动开关进行变化,使控制系统在特定条件下沿着预设的滑模面轨迹作高频小幅的趋向运动,而SMC所处的滑动状态则对控制系统参数和扰动均有较好的鲁棒性[6]。但在实际工作环境中,因为切换式起动开关的惯性影响,滑动模型无法正确到达所选择的滑模面上,极易造成系统抖振,使得此架构在实际应用中受到制约,因此大量的国内外学者致力于无抖振滑动模型架构的研究。文献[7]引用了“内外层”概念,外层采取正常滑模调节,在内层采取连续反馈调节以此减弱抖振。文献[8]使用了一种可变率滑动模型架构有效地抑制了抖振。文献[9-10]使用了一种自适应增益的滑模调节方法,利用等效原理判断滑模动态,并以此切换增益函数值,减弱抖振,增强系统的鲁棒性:文献[10]更在此理论基础上提出了快速自适应调整增益。文献[11-13]均使用了将积分项引入滑模面的设计工作中,以增加对传统滑模控制的鲁棒性。但是,这种方法的主要改进在于快速的负载变换将会产生面积饱和,从而导致超调量增大,执行机构无法进行下一步动作，引起系统不稳定甚至崩溃。

本文在原有研究基础上在积分滑模中引入积分削弱调节因子φ，同时引入边界层概念，更加方便柔化整个控制过程，对层内的电机转速采样精度影响可以忽略，保持了滑模控制的鲁棒性特点，大大降低了滑模抖振效应，同时采用了Lyapunov函数去验证此种设计结构的优越性。最后,进行优化前后的模型数据对比，从仿真分析的角度验证该方法的正确性。

1 扰动分析

PMSM使用了矢量控制方法,在旋转dq坐标系下的PMSM数学模型为[12]

(1)

式中：ud、uq、id、iq分别为定子在同转速坐标系下d、q两轴的电压和电流；Ld、Lq分别为定子在同样坐标系下两轴的电感，Rs、ψf、ωe和ωr分别为定子相的电枢电阻、永磁体磁链、转子角速度和机械角速度；uf和J分别为摩擦系数和转动惯量；TL、Te分别为负载转矩和J电磁转矩。

旋转dq坐标系定义为在静止坐标系下，转子的运行电角度为θ，为了保持相对静止，设定电机定子产生的旋转磁场角速度和转子旋转角速度相同，该坐标系为dq旋转坐标系，与坐标系的图解关系如图1所示。

图1 旋转dq坐标系与静止坐标系关系图

在这种状态下，设计滑模面方程，根据式(1)定义PMSM系统状态量：

(2)

根据文献[14]设计滑模面，定义状态量如下：

(3)

定义以下变量和成立条件为

(4)

d(t)是外界扰动，且有如下条件成立：

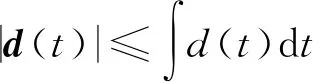
(5)

X(t)在与外界扰动d(t)进行滑模修正，定义跟踪误差为

(6)

采用传统滑模面：

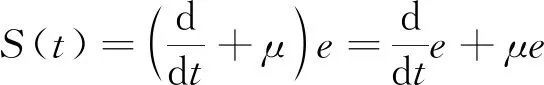
(7)

式中：μ为滑模面斜率，且μ>0。

通过滑模动态修正，使输出y(t)跟踪参考信号，yref(t)取式(1)的系统方程，取式(7)滑模面设计，控制信号取为

(8)

Q和C分别定义为

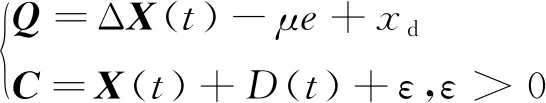
(9)

式中:xd为模糊有界函数最后变换后的误差补偿值,数值很小,可以忽略不记;D(t)为修正过后的外界扰动。

由此控制信号函数可知滑动模态是有界函数。

(10)

当s>0时，sgn(s)取1;当s<0时，sgn(s)取-1。

取Lyapunov函数2个条件如下：

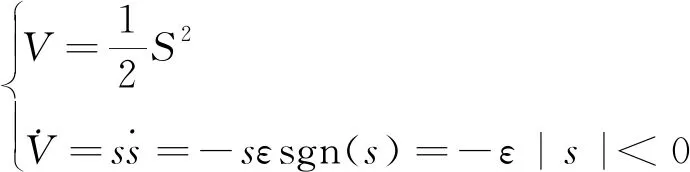
(11)

那么当s=0时，控制信号状态输入量即稳定滑模面上。

为了防止SMC出现抖振效应，传统控制算式通常采用收敛边界层的方式来平滑控制量，即在式(7)中重新引入一个函数进行收敛：

(12)

式中：γ为边界层厚度;sat[S(t)/γ]为与边界层有关的收敛函数。

sat[S(t)/γ]定义为

(13)

(14)

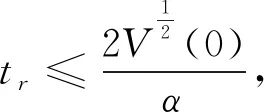
因Lyapunov条件的改变，式(11)也要做出相应改变：

(15)

(16)

得到ε的先决条件，则式(7)在边界层内部|S(t)|≤μ的运动轨迹可表述为

(17)

(18)

(19)

(20)

根据式(17)，通过终值定理，有下式成立：

(21)

同理可得:

(22)

由式(21)、式(22)，滑模面的斜率μ与滑模的趋近效果有关，变化率k分别取0、5、10，观察到通过增大k可以更快趋近滑模面，滑模扰动因素影响着整个体系的稳态误差,与滑模面斜率μ的变化率k之间成反比,与边界层面积γ成正比,若将滑模面斜率μ取大，则需更多的时间在滑模面进行处理，削弱了系统结构鲁棒性；若变化率k取大,系统的抖振会加剧；若γ取小，则抖振削弱的效果较难达到。即该传统模式的积分SMC并不能满足系统稳定性和超调性的控制要求。图2为不同斜面变化率k值的变化相轨迹。

图2 不同斜面变化率k值的变化相轨迹

2 带积分削弱型的SMC设计

2.1 抑制稳态误差

(23)

从结论1中的分析可以得出,当系统内部出现扰动的时候,对积分项的引入就会产生过饱和效应,进而产生更大的超调,甚至会引起整个系统的崩溃,所以需要对积分项进行微分削弱,并设计一个改进型的SMC,即：

(24)

式中：φ为削弱调节因子，φ≥-1。

分以下情况讨论：

(1) 当S<-μ时，有：

(25)

(2) 当S>μ时，有：

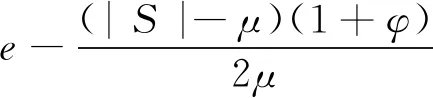
(26)

(3) 当|S|≤μ时，有：

(27)

2.2 削弱调节因子设计

图3 削弱积分型SMC仿真模型

(28)

用Lyapunov函数进行变化：

(29)

由终值定理可知：

(30)

由此比较结论1与结论2,可以得出,与传统SMC控制比较,引入了削弱积分模型的SMC可以更有效地控制的稳态误差情况,从而减少抖振效果,并且由于在边界层外对积分效应做出了削弱,也杜绝了超调情况的发生。

3 仿真分析

运用MATLAB/Simulink搭建削弱积分型PMSM调速模型进行仿真验证，电机参数如下。图4为带削弱积分型SMC的PMSM控制系统。

图4 带削弱积分型SMC的PMSM控制系统

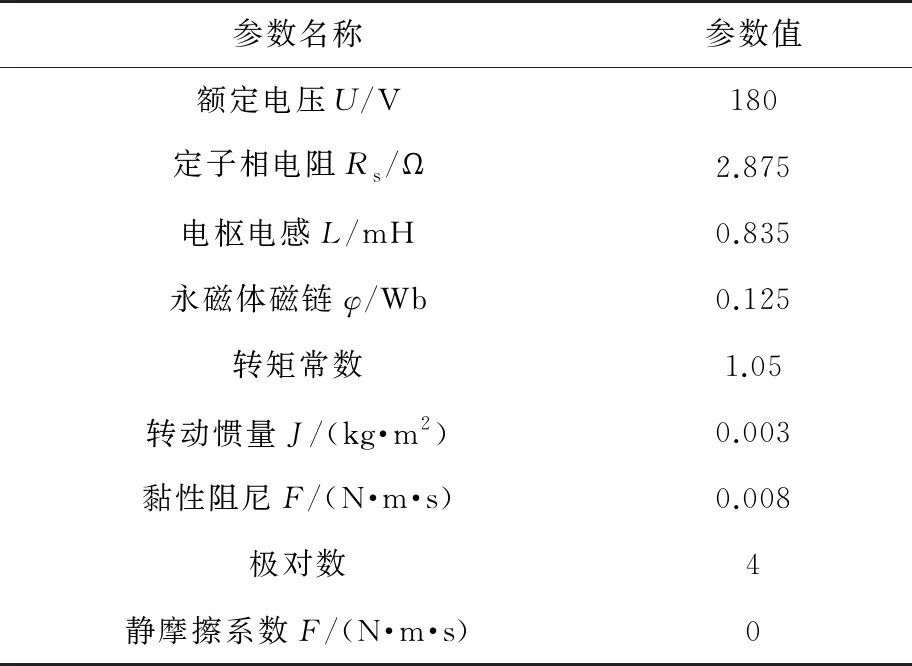
表1 仿真模型的参数

设定额定转速为2 000 r/min；电流环、电压环采样周期分别为200、100 μs；采样空间矢量脉宽调制(SVPWM)周期为150 μs。采用2种控制策略，控制器采用传统的积分型滑模面控制策略，控制器1取参数：

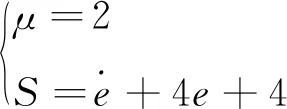
(31)

控制器2采用削弱积分型滑模控制策略，取参数：

(32)

滑模边界层均设为γ=2，变化率k均为2。分2种情况进行仿真，在0～0.5 s时，切换负载状态，切换为原负载转矩的2倍。分析转速情况和电磁转矩情况，定子电流情况在2种控制器中均无明显变化，观察控制效果最明显的转速变化，发现控制器1，在采用传统积分型SMC的时候，在系统起动时存在一个超调，在进行负载切换时，有一个明显的转矩下坠，且在2 000 r/min中上下波动将近200 r/min，如图5所示。图6为削弱积分型SMC转速波形图。分析电磁转矩时，控制器在初起动时波形严重失真如图7所示。因为对积分环节进行了削弱，所以对比采用削弱积分结构的SMC。由图5～图8可知，不论是在转速调节中还是在电磁转矩中的波形反应情况，均能有效抑制超调，并且具有较小的稳态误差，能够柔化控制过程，起到稳定控制的效果。

图5 传统SMC转速波形图

图6 削弱积分型SMC转速波形图

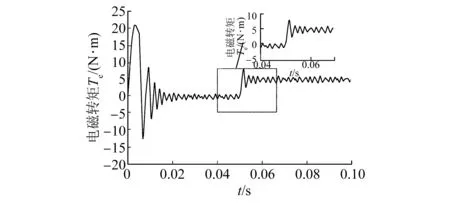
图7 传统SMC电磁转矩波形图

图8 削弱积分型SMC电磁转矩波形图

4 结 语

本文基于传统的SMC在PMSM上的运动,通过分析出现的问题,推导出由积分项过饱和而产生的稳态误差和超调量过大的原理,并分析了稳态误差与滑模面斜率、斜面变化率边界层厚度之间的关联,而削弱积分型SMC则是在利用了传统SMC设计的基础上,引入积分项来降低稳态误差，为防止超调过大，同时为了防止出现过饱和，对边界层外的积分进行削弱，改进了滑模面，有效地抑制了超调，提高了系统的鲁棒性。根据理论研究和仿真分析可以发现，与传统SMC相比,基于削弱积分型SMC在PMSM中的控制作用有以下有点：(1)有效抑制了电磁转矩的超调，减小了稳态误差，柔化了控制过程；(2)复杂性低，有利于后期使用级联H桥引入SVPWM控制。