基于VMD的永磁同步电机初期匝间短路故障检测方法
茅 宇, 杨 刘, 颜亮亮, 崔国庆
(江苏大学 电气信息工程学院,江苏 镇江 212013)
0 引 言
近年来,永磁同步电机(PMSM)由于其效率及功率因数高、转矩控制精准、结构简单和噪声低等优点,已广泛应用于航空航天、电动汽车、数控车床、智能机器人等高新技术领域[1-3]。但因功率密度大、安装空间狭小和散热环境恶劣等,PMSM的故障发生率较高。而电机作为系统重要核心部件,其可靠性将影响整个系统的性能,一旦发生故障,容易产生链式反应,导致整个系统瘫痪。PMSM在运行中通常出现的故障有匝间短路故障、偏心故障和退磁故障等,根据文献[4]的统计分析,匝间短路故障(ISCFs)约占21% ~37%。因此,实现电机早期匝间短路故障故障检测尤为重要[5-6]。
匝间短路故障诊断主要是基于振动信号频谱分析、电磁转矩分析和电机电流特征分析(MCSA)等分析来进行诊断的。但文献[7]还提出了一种利用指数判别分析(IEDA)提取和训练ISCFs的相电流信号的畸变特性,进行电机故障的诊断。在上述方法中,MCSA方法具有显著的优势,但也存在缺点,如由PMSM驱动电路产生的谐波信号与匝间短路故障引起的定子电流谐波信号叠加,使得故障信号无法被准确检测出。因此,在实际运用中,该方法的灵敏度较低[7]。文献[8-9]采用基于零序分量的诊断方法,克服了MCSA方法的局限性,并成功应用于电机的匝间短路故障检测。然而,PMSM发生初期匝间短路故障时,在零序电压分量(ZSVC)中代表故障特征的基波和五次谐波分量的幅值比正常情况ZSVC中包含的三次谐波分量和九次谐波分量的幅值小[10]。因此,在初期阶段的故障诊断中,故障特征容易被隐藏,使直接对ZSVC进行傅里叶频谱分析的方法失效,这就需要对传统的信号处理方法进行改进,从而提高故障检测的精度。
本文提出了一种基于ZSVC、变分模态分解(VMD)和双对数频谱分析的初期匝间短路故障检测方法。VMD是一种自适应、完全非递归的算法,抑制由模态混叠引起的噪声和冲击信号的影响,从而提高故障检测的精度。采用VMD去除ZSVC中的噪声和相关谐波分量以突出故障特征分量。利用双对数频谱分析对得到的信号进行分析,用于匝间故障检测。通过建立匝间短路故障的PMSM模型,并进行仿真和实物试验验证本文提出的故障检测技术。
1 带匝间故障的PMSM模型
图1为a相匝间故障时的PMSM等效模型,其中a1为故障部分,a2为健康部分。故障电流if表示短路匝内的循环电流。具有匝间故障的三相PMSM的电压方程可表示为[11-14]
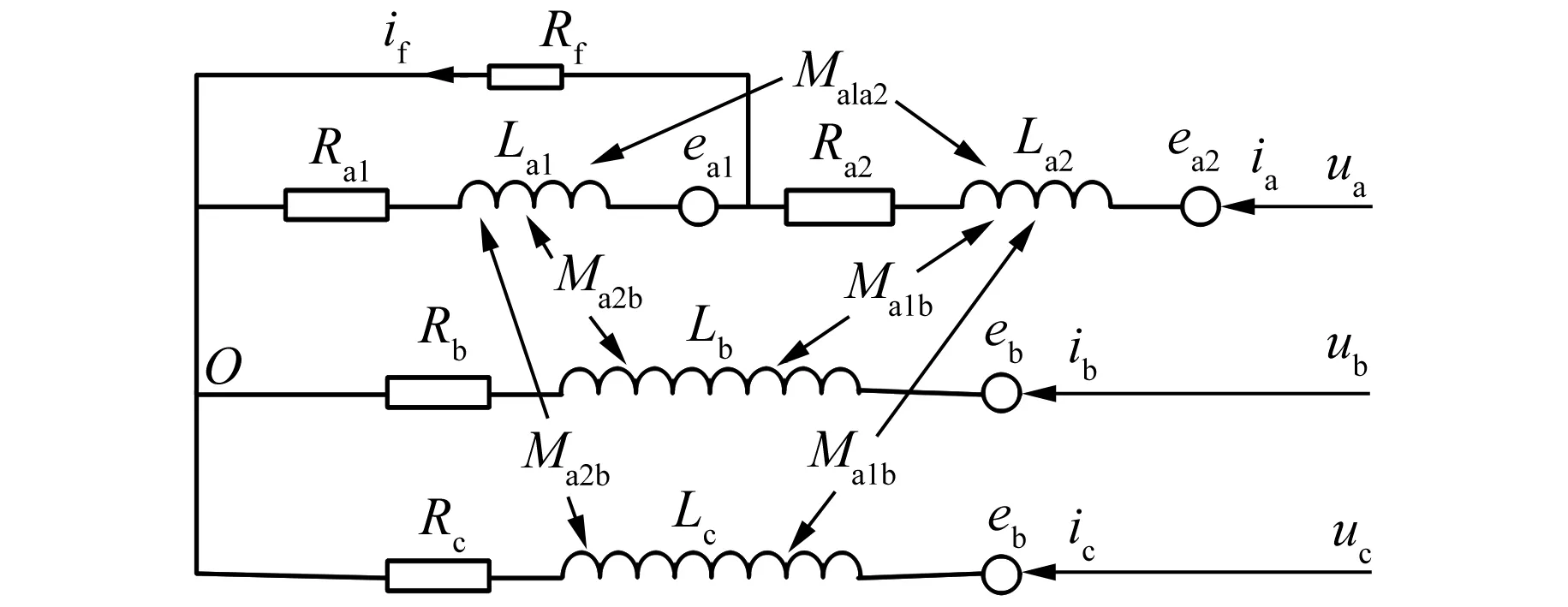
图1 PMSM的a相匝间故障等效模型

(1)

式中:Uf,abc为定子绕组的相电压矩阵;ua、ub、uc分别为三相电压;Rs为定子电阻;Rsf为电阻矩阵;Rf为短路电阻;η为短路匝数比,η=n/N,n和N分别为a相定子绕组的短路匝数和总匝数;If,abc为电流矩阵;ia、ib、ic分别为三相电流;if为故障电流;Lsf为电感矩阵;LAA、LBB、LCC分别为三相绕组的自感;MAB、MBA、MAC、MCA、MBC、MCB分别为三相定子绕组之间的互感;ψsf为绕组磁链矩;ψPM,a、ψPM,b、ψPM,c分别为三相磁链;ψPM,f为短路绕组磁链;U0为中性点电压矩阵;u0为中性点电压差。

(2)
式中:k为正整数;ψPM,1为基波磁链幅值;ψPM,i为第i次谐波磁链幅值;θ为转子电气位置;θi为第i次谐波磁链与基波磁链之间的夹角。
匝间短路故障下的PMSM电磁转矩可以表示为
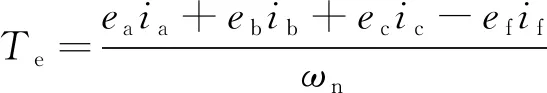
(3)
式中:ωn为PMSM转子机械角速度,ωn=ωe/p,ωe为转子电角速度,p为PMSM的极对数;ea、eb、ec分别为PMSM旋转时,永磁体转子在A、B和C相定子绕组中产生的反电动势。
2 故障诊断
2.1 ZSVC原理
本文研究的是基于ZSVC的匝间短路故障诊断,其带电阻网络的零序电压检测图如图2所示。u0表示逆变器直流电压中性点与定子绕组中性点之间的电压差,u0可表示为[15]
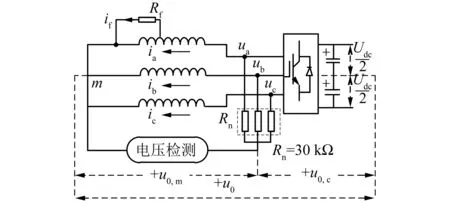
图2 带电阻网络的零序电压检测图

(4)

由式(4)可以看出u0受到逆变器的影响。因此,为了使u0摆脱逆变器的影响,采用三相平衡电阻网络[16-17]。图2中的参数u0,m可以不受PMSM逆变器的影响,u0,m可以表示为

(5)
正常运行的PMSM中不存在故障电流if,式(5)中u0,m只与ψPM,0的时间导数有关。由式(5)可知,在正常运行的PMSM中,u0,m仅由三次谐波分量及其奇次倍谐波分量组成。然而,在具有匝间短路故障的PMSM中,由于故障电流if的存在,u0,m不仅含有ψPM,0,而且含有if。if包含基波、三次谐波、五次谐波等奇次谐波分量。
因此,在发生故障的PMSM中,u0,m除了三次谐波分量及其奇次倍谐波分量外,还有新增的谐波分量,如基波、五次谐波和七次谐波等。在这些新增的谐波分量中,基波与五次谐波分量幅值相对较大,且对匝间短路故障的特征检测也最为敏感。因此,选用基波与五次谐波分量作为匝间短路故障的标志。
2.2 VMD算法
VMD算法是一种将信号分解为快速和慢速振荡的完全非递归模态变分方法,是一种具有自适应性、非递归性和准正交性的信号分解方法。VMD利用变分原理将信号分解为K个本征模态函数(IMF)。假设每个IMF均是具有一个中心频率的有限带宽信号,为求中心频率ωk和IMFs的uk,VMD采用交替方向乘子法(ADMM)算法求解约束变分问题。VMD的具体操作分为变分问题的构造和变分问题的解。
2.2.1 变分问题的构造
(1) 利用希尔伯特变换计算各阶模态函数的解析信号及其单侧谱:

(6)
式中:δ(t)为脉冲函数;j为虚数单位;*为卷积符号;uk为变分模态分解到的第k个IMF分量。
(2) 将每个模态频谱调制到相应估计中心频率:
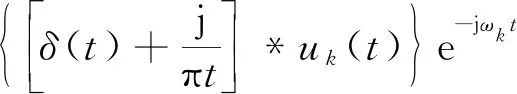
(7)
(3) 通过高斯平滑解调估计每个模式的带宽,从而得到约束公式如下:
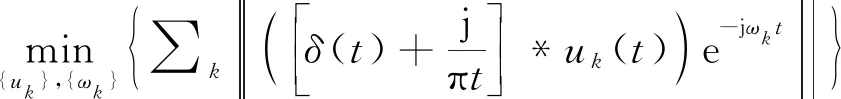
(8)
2.2.2 变分问题的解
(1) 通过引入惩罚参数α和拉格朗日乘子因子λ来解决约束变分问题:
L({uk},{ωk},{λ})=
∑kuk(t)>
(9)
式中:f(t)为给定的原始信号。
(2) 应用ADMM得到上面表达式的鞍点。因此,使用下面的表达式更新模态uk:

(10)
(3) 利用Parseval/Planchcrel傅里叶等距将上述问题转换到光谱域:

(11)
(4) 使用ω-ωk替换ω的变化:

(12)
将式(12)转化为非负频率区间积分形式:

(13)
这个二次优化问题的解如下:

(14)
将中心频率问题转化为傅里叶域,最终得到优化:
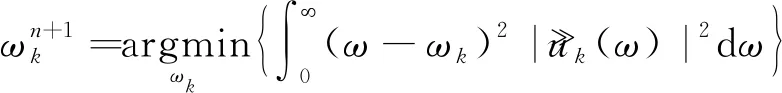
(15)
最后,得到中心频率的更新:

(16)
VMD的计算过程:
步骤2 使n=n+1,执行循环程序。
步骤3 根据式(9)和式(11)更新uk和ωk。
步骤4 使k=k+1,重复步骤3,直到k=K。
2.3 故障诊断流程
为了提高基于ZSVC的故障诊断方法的性能,提出了对ZSVC信号进行VMD分析,得到包含三次和五次谐波的IMF分量。然后对IMF分量进行双对数频谱分析,通过观察基波与五次谐波分量幅值的变化来检测匝间短路故障。此外,为了进一步详述所提出的方法,设计了如图3所示的故障诊断流程图。
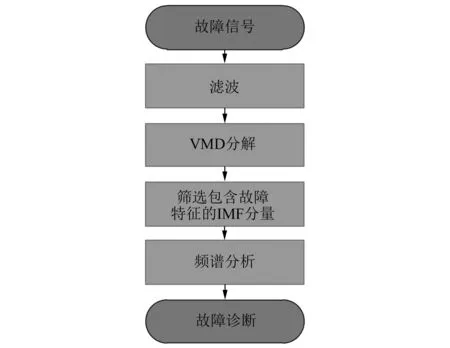
图3 故障诊断流程图
3 仿真分析
3.1 联合仿真模型
采用Simulink、ANSYS Maxwell与ANSYS Electronics对本文所提方法进行联合仿真分析。PMSM的主要参数如表1所示,搭建的联合仿真模型如图4所示,该仿真系统包含了三相逆变桥、PMSM有限元模型、空间矢量脉宽调制(SVPWM)和Simulink与ANSYS Electronics链接部分等模块。

图4 联合仿真模型图
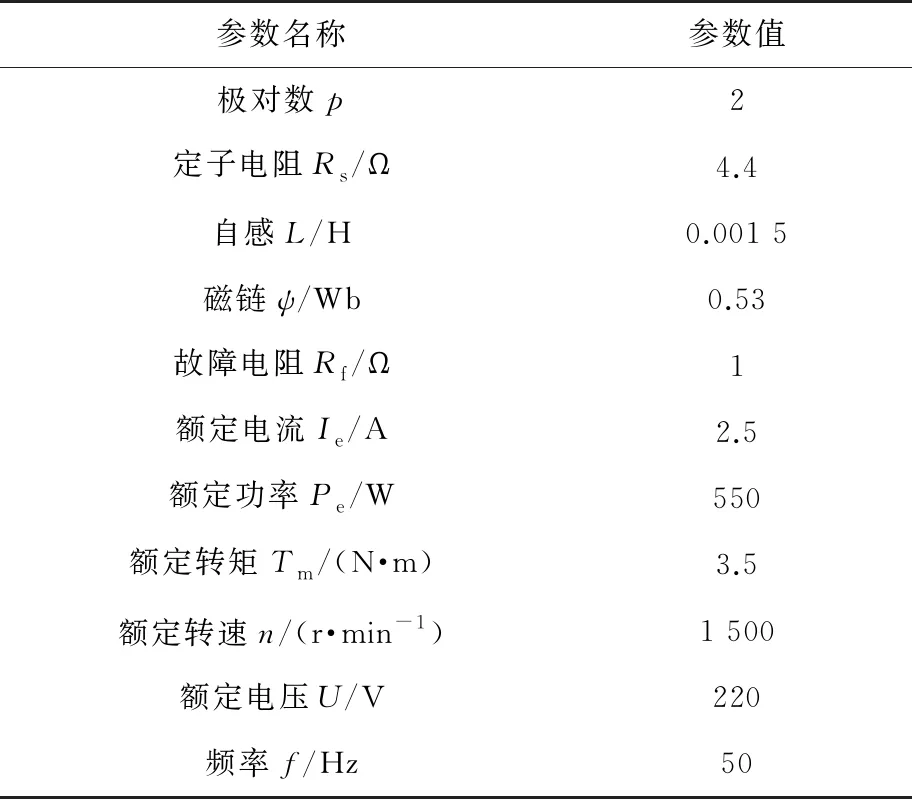
表1 PMSM的主要参数
3.2 基于ZSVC的故障诊断
图5(a)和图5(b)分别给出了PMSM在参考转速为480 r/min,基波频率f1=n×p/60=16 Hz,负载转矩为2 N·m,短匝比η为0.03,Rf=1 Ω,正常和匝间短路故障工况下的ZSVC波形。当匝间短路故障发生时,与正常情况相比,u0,m中理论上出现了基波(16 Hz)和五次谐波分量(80 Hz)。然而,当匝间故障发生初期,与三次谐波、九次谐波等其他谐波分量相比,基波和五次谐波分量的幅值很小,如图6所示,无法准确检测出基波和五次谐波。
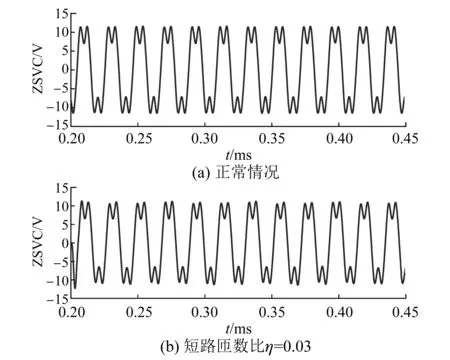
图5 正常和故障情况下的ZSVC波形

图6 正常情况和短路匝数比为η=0.03时的ZSVC频谱分析图
本文针对初期匝间短路故障采用双对数频谱分析难以检测故障的问题,提出了具有强抗噪能力的VMD与双对数频谱分析相结合的方法。采用VMD去除ZSVC中的噪声和相关谐波分量以突出故障特征分量。然后利用双对数频谱分析对得到的信号进行分析,提取故障特征。
按照图3所示流程图对故障信号进行处理,对ZSVC信号进行VMD,经试验及查阅相关资料,得出惩罚因子为α=2 000,DC=0,t=0,tol=10-7,ε=10-7。VMD受分解模态数K值的影响较大,K较小时,会滤除掉重要信息;K较大时,分解时会产生模态混叠,根据中心频率进行模态数的选取,不同K值时的各模态中心频率如表2所示。

表2 不同K值时各模态的中心频率 Hz
由表2可知,当K=2时,第二分量的中心频率为141 Hz,导致中心频率为240 Hz的模态信息丢失;当K=4时,第四分量的中心频率为19 Hz,导致模态过分解现象,因此K的值选3较为合适。
对ZSVC进行VMD分解,图7所示为短路匝数比为η=0.03时的ZSVC的VMD分解图。其中IMF1对应的中心频率为47 Hz,而包含了故障信息的基波和五次谐波为16和80 Hz,因此选取IMF1作为故障后续处理信号。

图7 短路匝数比η=0.03时的ZSVC的VMD分解图
图8~图10为不同短路匝数比时的ZSVC频谱图。从图8~图10中可以明显观察到故障特征频率基波与五次谐波信号,其中基波幅值大于五次谐波幅值,且随着故障短路匝数比的增大,基波和五次谐波分量幅值越大,越容易识别出故障信号。

图8 短路匝数比η=0.03时的ZSVC频谱图

图9 短路匝数比η=0.02时的ZSVC频谱图

图10 短路匝数比η=0.01时的ZSVC频谱图
4 实物试验
试验平台主要包括3部分:电源系统、电机拖动系统及数据采集系统。电源系统主要由50 Hz工频电源和西门子M440变频器2部分组成。电机拖动系统主要由PMSM、直流电机以及电阻箱组成。数据采集系统主要由电流传感器、示波器及数据采集卡组成。
如图11所示,被测试的设置匝间短路故障的PMSM与给PMSM施加负载的磁粉制动器通过一个联轴器直接连接。为了消除逆变器的影响,采用图2所示的三相平衡电阻网,电阻网中的电阻值为30 kΩ。除Rf外,用于实物试验的PMSM的主要参数与用于仿真分析的相同。在本试验中,测试用PMSM的匝间故障是通过将绕组抽头与一根导线连接的。根据短路匝数比公式η=n/N,A5、A10、A15和A20是对应的4个短路匝数,其与总匝数的比就是对应的短路匝数比。试验中,PMSM的转子转速为480 r/min,采样频率Fs为5 000 Hz。此外,应该注意的是,随着被测试的PMSM匝间短路故障的匝数增加,PMSM处于高速运行时可能导致较大的短路电流,所以在短路绕组间串联一个故障电阻Rf(Rf=7 Ω),且使电机处于低速状态下进行试验,避免出现较大的故障电流损害被测试的PMSM定子绕组。

图11 试验平台及短路绕组结构
图12和图13分别为正常情况下ZSVC的波形及频谱。将对正常情况时的ZSVC进行VMD分解,结果如图14所示。图15和图16分别为短路匝数比η=0.1时故障条件下ZSVC波形及频谱。由于振幅很小,谐波分量和噪声,基波分量在频谱中几乎观测不到。为了检测基频,对故障条件下的ZSVC进行VMD分解,结果如图17所示。
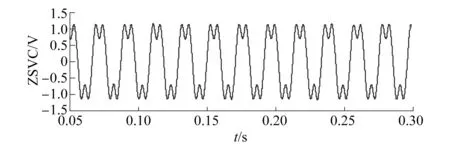
图12 正常情况ZSVC波形

图13 正常情况ZSVC频谱

图14 正常情况时的ZSVC的VMD分解图

图15 η=0.1匝间故障ZSVC波形

图16 η=0.1匝间故障ZSVC频谱
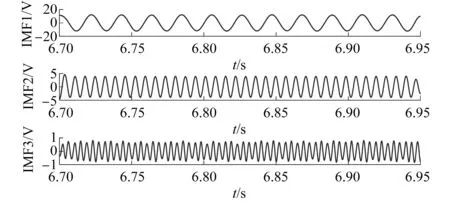
图17 短路匝数比为η=0.1时ZSVC的VMD分解图
图18为正常情况时的IMF1频谱图,没有基波和五次谐波频率。图19和图20为η=0.05和η=0.1的匝间故障条件下IMF1频谱分析图,可以明显观察到基波频率和五次谐波频率。
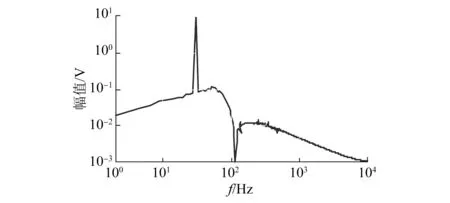
图18 正常情况时的IMF1频谱图

图19 短路匝数比为η=0.05时的IMF1频谱图

图20 短路匝数比为η=0.1时的IMF1频谱图
5 结 语
PMSM匝间故障在发生初期,由于其故障特征容易被干扰,通常难以准确检测出故障特征信号。因此,本文提出了一种基于VMD与双对数频谱分析的PMSM匝间短路故障诊断的方法。采用VMD与双对数频谱分析方法对ZSVC信号进行分析,得到故障特征分量。仿真和实物试验结果表明,该方法对PMSM匝间故障的早期诊断是有效的。
同时,需要注意的是,测量ZSVC需要一个可接近的定子绕组中性点。文中采用电阻网络是在不破坏电机原有的结构情况下进行试验的。而容错PMSM驱动系统的中性点是可访问的,将所提出的故障检测方法与容错方法相结合,可以大大提高PMSM驱动系统的可靠性。

