直线电机推力波动补偿技术

沈海涛, 汪 奇, 吉晓凯, 张 凯, 周 原

(苏州维嘉科技股份有限公司，江苏 苏州 215000)

0 引 言

永磁同步直线电机因其推力密度高、功耗低、响应速度快等特点而被广泛应用于印刷电路板(PCB)钻孔机、锣机、分板机、钻孔检测等高速、高精度数控系统，并得到了国内外学者的关注与研究[1-4]。

因初级铁心开断引起的边端力和因齿槽效应引起的齿槽力(合称磁阻力)[5-7]是引起直线电机推力波动的主要因素。而推力波动是直线电机产生振动和噪声的主要原因，特别是在低速运行时，推力波动会导致运动控制跟随误差变大[8]。因此，国内外学者对直线电机的推力波动进行了大量的研究。

文献[9]通过分析永磁同步直线电机推力波动的机理，指出推力纹波、齿槽效应和端部效应是引起永磁同步直线电机推力波动的最主要原因，探讨了减小永磁同步直线电机推力波动的技术措施。文献[10]采用半无限单端结构建立了由边端效应引起的磁阻力分析模型，并提出了优化初级长度从而降低磁阻力的原理与方法。文献[11]提出一种将磁极错位与V型磁极相结合的优化方法来改善其性能。同样地，也有学者在控制算法上对直线电机推力波动进行分析、抑制[12-13]与补偿[8,14-15]。

综上，本文提出一种直线电机推力波动补偿的方法，以一台6槽8极电机为研究对象，结合解析计算理论基础与有限元建模，分析并归纳永磁直线电机边端力与齿槽力的影响因素与一般规律。合理设置补偿器关键参数，有效补偿传统永磁直线电机磁阻力。通过试验，验证该补偿方法对直线电机推力波动抑制的正确性与精确性。

1 边端力分析与计算

考虑直线电机铁心开断的缘故，直线电机左右两端分别受到了两个边端力，其效果满足磁阻最小原理，即磁通总是沿着磁阻最小的路径闭合[15]。

1.1 直线电机边端力分析

对于直线电机边端力分析，其模型等效于无槽直线电机[10]，如图1(a)所示，其中初级铁心截面等效为一个矩形，因不存在齿槽结构，所以实现了分离齿槽力，仅分析直线电机边端力。初级铁心在不同位置受到的边端力不同，且分别受到两侧端部的力Fend_L和Fend_R，由于次级永磁体周期排列，相应的边端力就是次级极距的周期函数。同理补偿器模型亦可看作无槽直线电机，如图1(b)所示，其边端力特性与直线电机相同，唯一区别在于两者之间位置不同导致存在相位差，且补偿器尺寸更小。

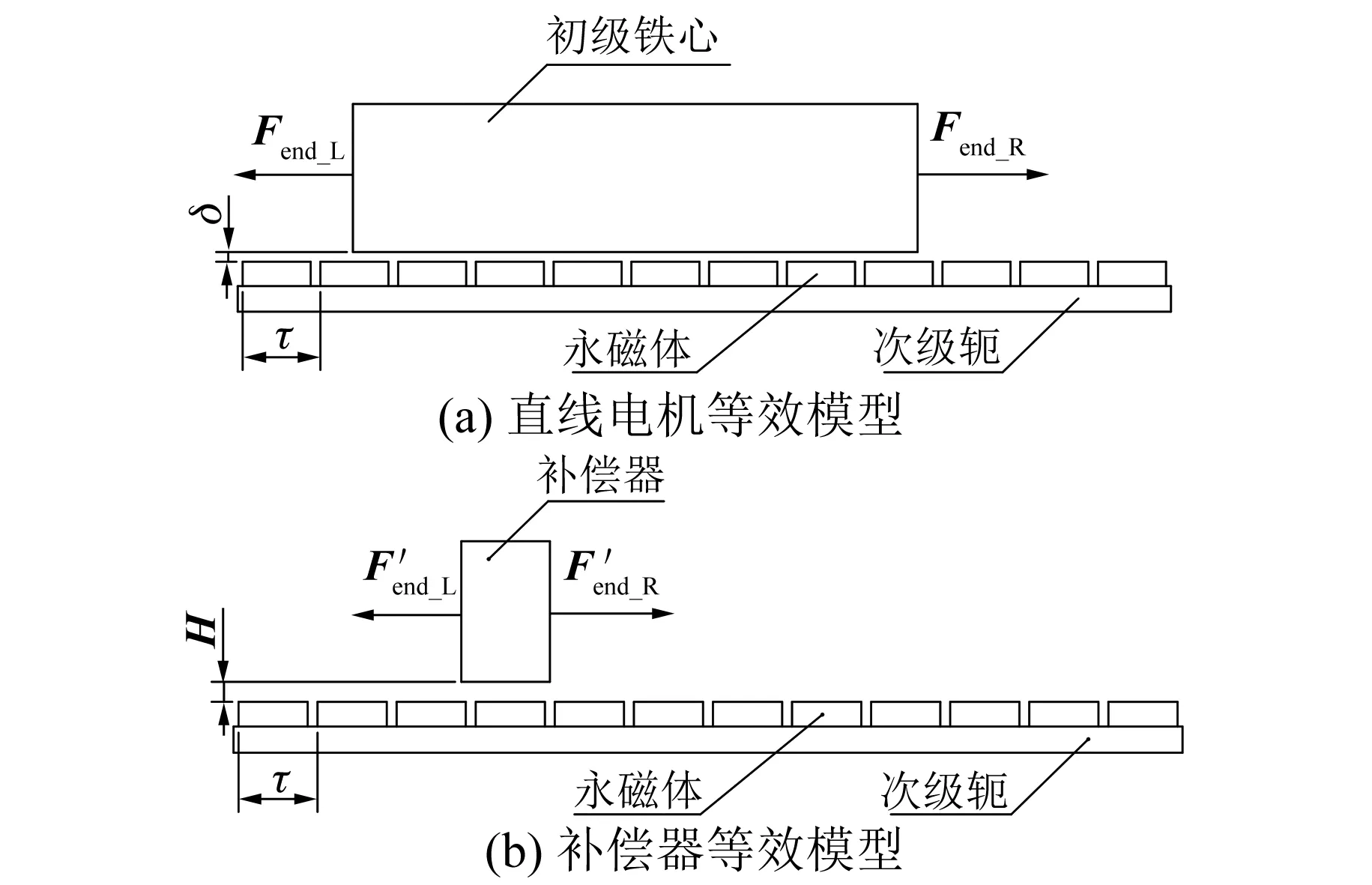
图1 边端力分析等效模型

为简化解析计算过程，作如下假设：

(1) 假设铁心磁导率无穷大，且不考虑饱和问题；

(2) 忽略漏磁，即漏磁系数σ=1；

(3) 永磁体的相对磁导率为1，也就是和真空状态保持一致；

(4) 只考虑法相磁场，不考虑运动方向和铁心叠压方向磁场变化。

根据电磁场相关理论可知，单位体积的气隙磁场储能为

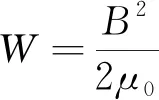
(1)

式中：B为气隙磁密；μ0为真空磁导率。

因此对于直线电机，根据虚位移原理可得，直线电机左侧边端力为

(2)

且有：

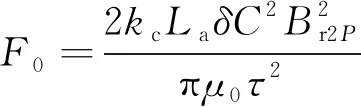
(3)

式中：La为电机初级铁心叠厚；δ为电机气隙长度；C为初级铁心长度;Br2P为2P次电机气隙磁密；τ为极距(N-S);kc为电机气隙系数。

同理，将x′=x+Δx代入式(2)(Δx=C-kτ，k为整数)，同时考虑右端力方向为正，因此可以得到右端部力为

Fend_R(x)=

(4)

因此直线电机边端力为

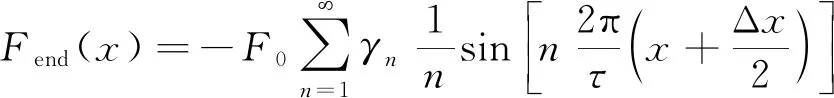
(5)

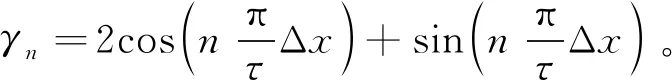
根据直线电机边端力解析式(5)可得如下结论：

(1) 边端力的基波频率为1/τ，即直线电机边端力频率为电机运行频率的两倍频；

(2) 当Δx=ατ时，其中α为整数，电机合成边端力幅值最大；

(3) 当Δx=(2m-1)τ/2时，其中m为正整数，电机合成边端力幅值最小，其基波幅值理论为0。

图2所示为无槽电机边端力幅值在Δx=(0～2)τ范围内的有限元和解析计算结果。由图2可见，边端力的基波频率为1/τ，且仿真结果和解析计算结果基本一致。为了获得最低的边端力以及最短的直线电机长度(直线电机长度会影响行程)，因而Δx=τ/2，即电机长度(初级铁心长度)C=kτ+τ/2。

图2 无槽电机边端力幅值

1.2 补偿器边端力分析

为了能抵消直线电机产生的边端力，因而期望补偿器能产生一个与直线电机边端力频率相同、幅值相同、相位相反的边端力。

补偿器模型如图1(b)所示，同理补偿器亦可看作是一个无槽直线电机，因此其边端力为

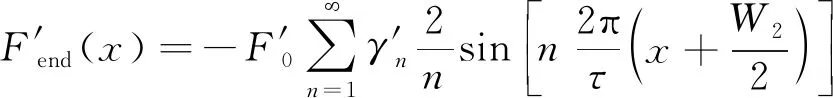
(6)

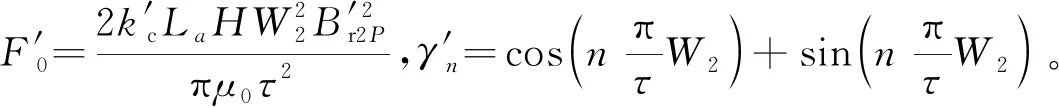
式中：H为补偿器气隙长度;W2为补偿器长度;B′r2P为2P次补偿器气隙磁密;k′c为补偿器气隙系数。

显而易见补偿器边端力与直线电机具有相同的频率和分布特性，边端力分布与图2类似。考虑到更小尺寸的补偿器产生更大的边端力F′end用以抵消直线电机产生的边端力Fend，因此参见图2，补偿器最佳长度为W2=τ。

图3所示为直线电机及其补偿器等效模型，其中补偿器无齿槽结构。根据上述分析，此结构补偿器可以产生一个与电机边端力波长τ相同的边端力谐波，因而只需补偿器产生的边端力谐波与电机的幅值相同，相序相反。

图3 直线电机及其补偿器等效模型

根据式(5)与式(6)，令∠Fend-∠F′end=180°得直线电机与补偿器中心线之间的距离W1为

(7)

因W1≥W2/2，综合考虑电机初级总长度，最佳的距离在k=1时，W1=5τ/4。

同理，令|Fend|=|F′end|，可得补偿器气隙长度H为

(8)

2 齿槽力分析与计算

由初级铁心齿槽结构和永磁体相互作用产生的齿槽力，是永磁直线电机的另一重要参数，其存在同样能造成电机的推力波动，进而产生速度波动、振动和噪声。

2.1 直线电机齿槽力分析

与旋转电机齿槽转矩类似，直线电机齿槽力是电机在不通电的情况下，永磁体和齿槽间的相互作用力，其齿槽力表达式为[16-20]

(9)

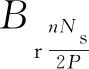
2.2 补偿器齿槽力分析

将补偿器同样开出齿槽结构，如图4所示。其齿槽力表示如下：

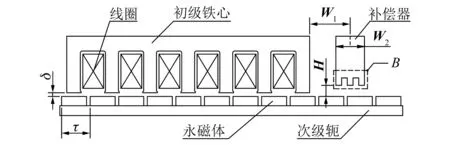
图4 电机及补偿器(带齿)模型

(10)

前面分析到，补偿器最佳长度为W2=τ，即对于补偿器，其极对数2p=1，因此式(10)中的整数a最小值为1。也就是说，补偿器齿槽力基波次数与其齿数Nt一致。此时公式(10)可改写为

(11)

表1为不同单元电机补偿器齿数汇总，从表1中可发现补偿器齿数与单元电机初级齿数相等。

表1 不同单元电机补偿器的齿数

3 仿真结果与分析

为验证上述解析方法的正确性与准确度，以6槽8极电机为例，如图4所示，对电机进行有限元仿真分析，电机与补偿器基本参数见表2。其中6槽8极电机单元电机为3槽4极电机，参见表1，Nt=3。

表2 电机与补偿器参数

3.1 边端力仿真计算

前述提到，在分析边端力时，可将电机和补偿器均看作无槽直线电机，如图1所示。

图5(a)为单独直线电机与补偿器边端力有限元仿真和解析计算结果，可以看出在一个电周期2τ内，电机与补偿器边端力均波动了2次，也就说明边端力波长为τ，与前述分析结果一致。同时可以看出直线电机边端力与补偿器边端力相位相反，因而能起到抑制电机边端力的作用，且解析结果与有限元仿真结果基本保持一致。

图5(b)为搭配所述补偿器后，直线电机合成边端力有限元仿真与解析计算结果。解析计算合成边端力为0，而仿真数据仍含有幅值为1.3 N的4次谐波，主要原因是解析计算只计算了2次谐波，而有限元仿真还包含4次、6次、8次等谐波。但是从效果上看，边端力23.6 N降低到1.2 N，降幅高达94.9%，效果显著。

图5 边端力计算曲线图

3.2 齿槽力仿真计算

对直线电机齿槽力进行仿真分析，需对仿真模型作如下设置，如图6所示，即设置周期边界，此时可忽略动子铁心开断引入的边端力。同样地对补偿器亦作类似设置。

图6 齿槽力仿真模型

图7(a)为单独直线电机与补偿器齿槽力有限元仿真和解析计算结果，可以看出，6槽8极直线电机在一个电周期2τ内，齿槽力周期数为6，即符合前述分析一个极距τ内，齿槽力周期为nNs/2P=4×6/8=3。且补偿器齿槽力周期同样满足上述分析。但补偿器齿槽力幅值较直线电机齿槽力小得多，具体见图7(a)和图7(b)。图7(c)为直线电机与补偿器合成齿槽力，齿槽力仿真数据从5.5 N降低为4.4 N，仅降低20%，结合式(7)和式(8)，可以发现齿槽力幅值与直线电机初级长度C(对于补偿器为W2)正相关，而本文中C≫W2。因此，补偿器对齿槽力削弱效果不明显，且解析结果与有限元仿真结果基本保持一致。

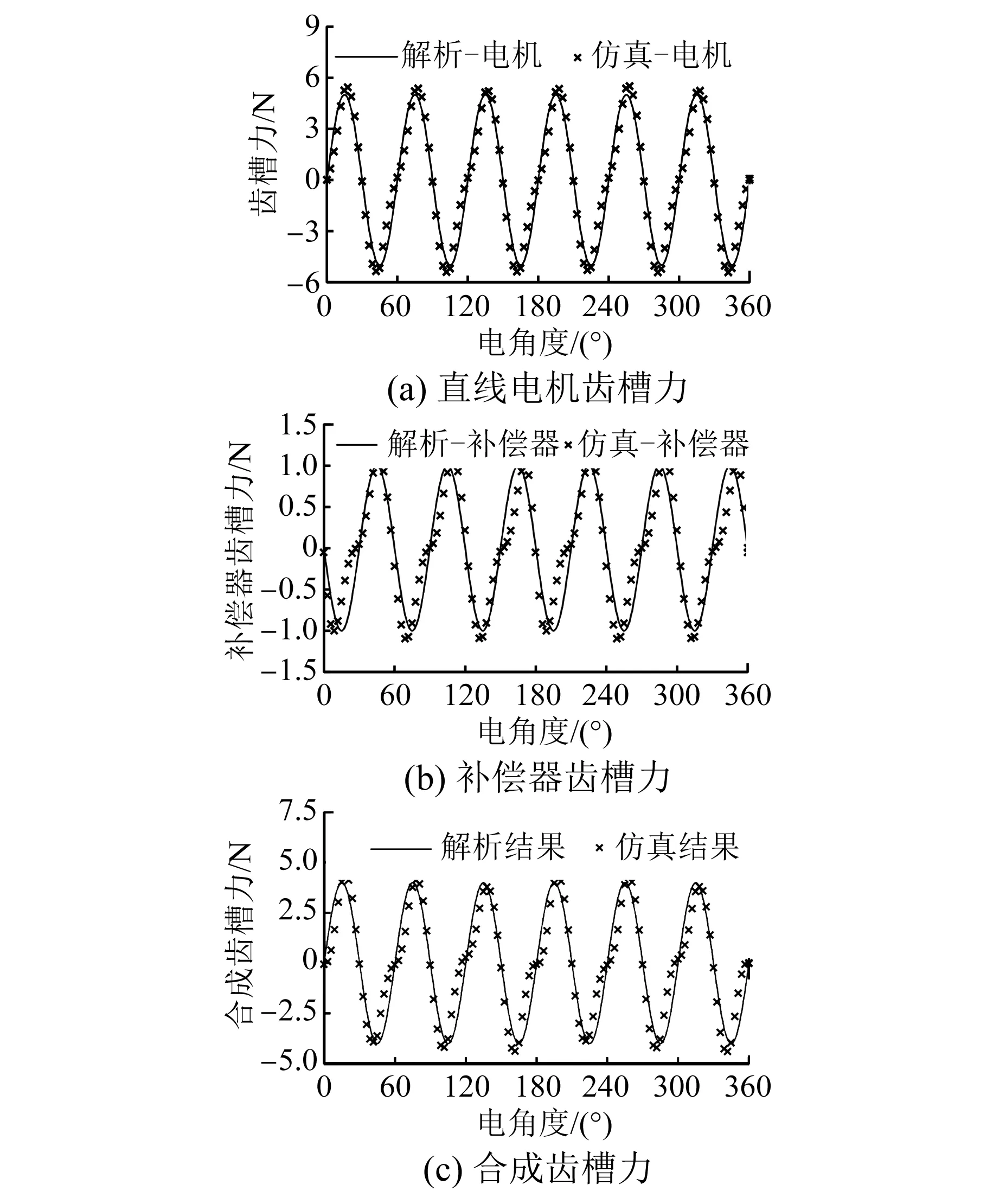
图7 齿槽力计算曲线图

3.3 磁阻力仿真计算

图8为补偿前后(模型如图4)直线电机磁阻力有限元仿真与解析计算结果。可以看出，补偿前后，直线电机磁阻力仿真数据从23.9 N降到了7.2 N，补偿效果达到69.9%，十分显著。解析结果与有限元仿真结果基本保持一致，其中补偿前仿真数据较解析数据大的原因在于解析仅对边端力的2次谐波、以及齿槽力的6次谐波进行分析，而仿真数据包含其他高次谐波。

图8 6槽8极直线电机合成磁阻力波形

4 试验验证

为了验证解析计算与有限元分析的合理性与准确性，利用直线电机测试台并配合高精度力传感器，分别对测试台、电机、补偿器以及搭配补偿器的直线电机磁阻力进行了测试。测试数据参数如表3所示。图9(a)所示为对拖电机拉着被测电机安装板情况下的测试台自身的磁阻力波形，分为正、反两个方向，因为对拖电机本身同为有铁心直线电机，同样具有磁阻力，同时因为测试台的抖动、摩擦力不均匀等，所以此时磁阻力波形为非理想恒值波形，具有些许波动，波动力达到14.5 N。

表3 电机与补偿器磁阻力测试数据

图9(b)所示为本文所述6槽8极电机磁阻力测试波形，显而易见磁阻力主要谐波含量为2倍频(τ=15 mm)，且磁阻力谐波的幅值为28.7 N，为仿真数据的83.7%(前述仿真数据为23.9 N)。其中正、反方向波形相位、幅值、频率均基本保持一致，存在的偏置主要是由摩擦力造成的。图9(c)所示为补偿器磁阻力测试波形，其磁阻力波形与直线电机波形谐波含量相同，但相位相反。因此，补偿器能够实现直线电机磁阻力补偿，且与理论分析结果一致。图9(d)为本文所述补偿器与直线电机相配合下的磁阻力测试波形，此时的磁阻力仅为11.8 N，补偿器补偿磁阻力效果达到60.8%(仿真为69.9%)，且合成磁阻力的2倍频谐波已经基本消除。仿真数据与测试数据的差别主要在于前述分析的测试台本身误差以及有限元仿真剖分等综合因素造成的。

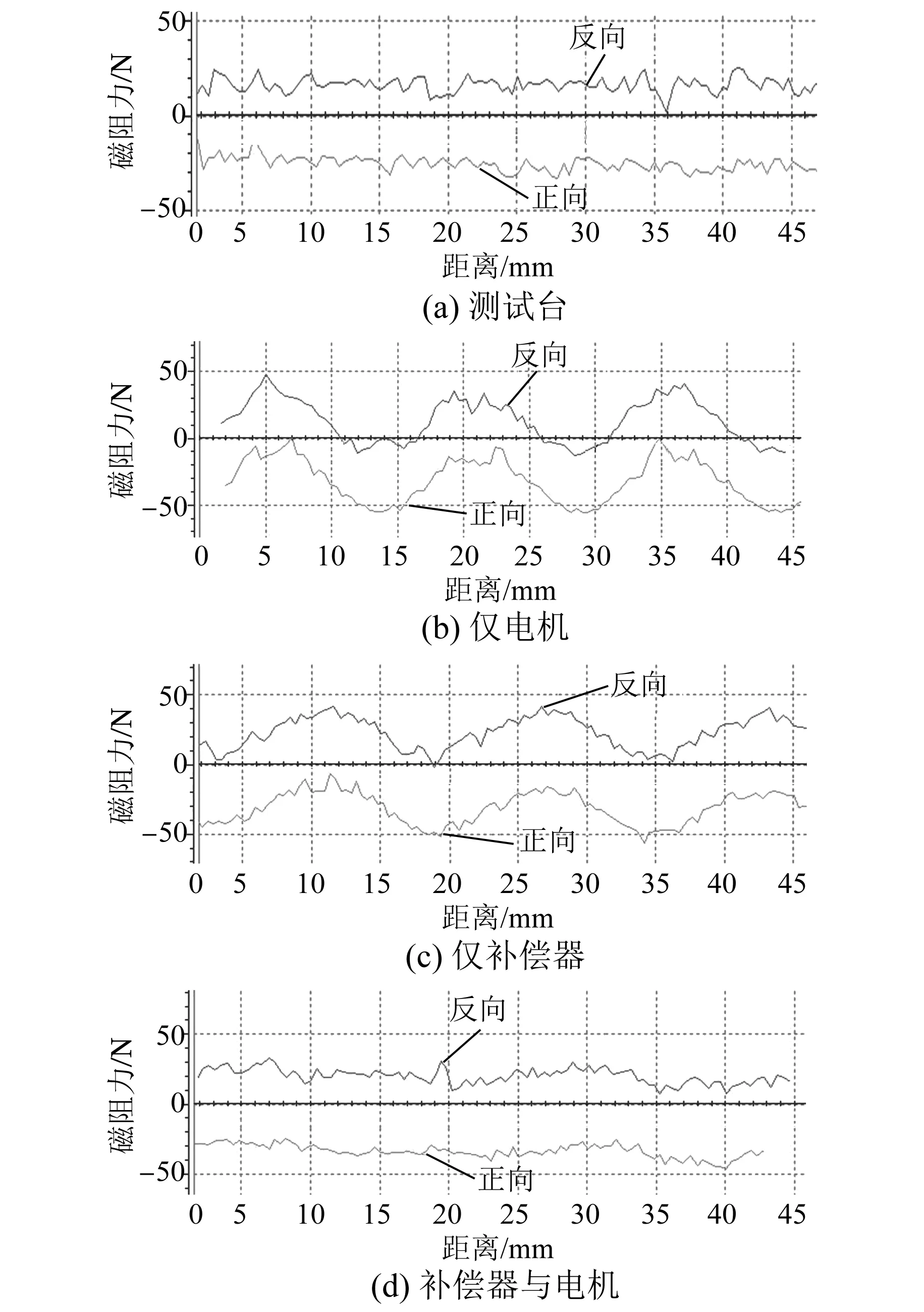
图9 6槽8极直线电机磁阻力测试波形

5 结 语

本文提出一种直线电机推力波动补偿的方法。将引起直线电机推力波动的力(本文称之为磁阻力)分为两种分量:(1) 由于直线电机初级铁心的开断而产生的力，称之为边端力；(2) 由于齿槽效应而产生的力，称之为齿槽力。其次通过解析法，精确计算并归纳边端力与齿槽力的一般规律，并合理设置补偿器参数。然后，以一台6槽8极电机为例，将解析结果与仿真结果相比较，并进行了试验验证。结果表明本文所述补偿器能实现直线电机磁阻力补偿，对直线电机推力波动具有较好的抑制效果。