具有共模电压抑制能力的PMSM混合模型预测转矩控制*

陈致君, 王 涛, 刘 闯, 朱姝姝, 张 曦

(1.南京航空航天大学 自动化学院，江苏 南京 211106；2.南京航空航天大学金城学院 机电工程与自动化学院，江苏 南京 211156)

0 引 言

永磁同步电机(PMSM)具有较高的功率密度、效率和可靠性，在航空航天、电动汽车、精密伺服等领域应用广泛[1]。针对PMSM的高性能转矩控制，在多种工业应用场合具有重要意义，如汽车电动助力转向系统[2]、工业机器人关节电机[3]、飞机主动驾驶杆[4]等。

模型预测控制(MPC)动态响应快、抗扰动能力强，且能处理带约束的多目标优化控制问题，近年来在PMSM驱动领域获得了快速发展[5]。文献[6-7]针对PMSM转矩控制，在6个非零电压矢量和2个零电压矢量组成的电压矢量有限控制集中，通过价值函数最小化筛选出最优电压矢量，施加于电机系统，从而获得较快的转矩响应速度，但该类方法存在较大的转矩波动。对此，文献[8]采用非零电压矢量和零电压矢量合成虚拟电压矢量，并将其加入原有控制集，获得了较好的转矩稳态性能；同样为降低转矩脉动，文献[9]提出一种三矢量模型预测转矩控制(MPTC)，在一个采样周期中作用2个有效矢量和1个零矢量，其电压矢量合成的灵活性优于文献[8]所提虚拟电压矢量法，故可更好地抑制转矩脉动。

然而，上述MPTC均需使用零电压矢量，存在幅值为Udc/2的较大共模电压，可能引起电机轴电流，造成电机轴承和绕组绝缘损坏[10-11]，并产生电磁干扰，影响附近电子设备正常运行，尤其在航空、汽车等领域中，电磁干扰可能造成较严重的安全问题[12-13]。因此，共模电压抑制是PMSM MPC需要考虑的重要问题。目前，国内外学者已围绕MPC的共模电压抑制问题开展了较丰富的研究，文献[14]在MPC的价值函数中加入共模电压抑制项，但这种电压矢量的软性筛选机制无法完全抑制共模电压尖峰，且因其价值函数考虑了共模电压抑制项，造成了主要控制目标对共模电压抑制目标的妥协，降低了电流和转矩性能。文献[15-16]在MPC中，只使用6个非零基本矢量，而摒弃零矢量，从而抑制共模电压，但与常规MPC相比，其电流和转矩波动有所增加。为此，文献[17]中将非零矢量合成的虚拟矢量加入矢量控制集，在规避零矢量的同时，减小了电流和转矩波动。文献[18]提出在控制周期内使用2个非零电压矢量，计算各自的作用时间合成作用矢量，以获得比文献[17]更好的电流和转矩性能，但由于摒弃了零矢量，其仅能合成幅值较大的虚拟矢量(大于Udc/3)，电流和转矩性能提升较为有限。为在更大范围内灵活合成电压矢量，文献[19]采用2个方向相反的有效矢量作为等效零矢量，替换常规三矢量合成法[9]中的零矢量，可较好地抑制电流和转矩脉动，但其实质是采用4个有效矢量合成目标电压矢量，导致逆变器开关频率高、损耗大、散热困难，因此这种方法在许多实际应用场合中受到限制。综上所述，现有具备共模电压抑制能力的MPC方法难以兼顾开关频率和转矩性能2个重要指标。

本文结合文献[17]中虚拟矢量法和文献[19]中基于等效零矢量的多矢量合成法(下文简称多矢量合成法)的优点，提出一种混合MPTC策略，通过无差拍控制思想计算出参考电压矢量，根据参考电压矢量的不同幅值切换不同的电压矢量生成方法：(1)当参考电压矢量>预先设定的切换阈值时，采用基于非零矢量合成的虚拟矢量法，以在实现较好转矩性能的同时降低平均开关频率；(2)当参考电压<阈值时，可供选择的虚拟电压矢量均与参考电压矢量相差较大，虚拟矢量法将产生较大的转矩波动，已不宜使用，故切换为多矢量合成法，以较高的开关频率为代价获得较好的转矩控制性能。从全工况范围来看，本文所提混合MPTC只需较低的平均开关频率即可实现共模电压抑制，有利于减小开关损耗，提高电机控制效率，并可兼顾保证良好的转矩静、动态控制性能，十分适合于航空航天、汽车、工业机器人等对转矩控制性能要求较高,同时对共模电压十分敏感的应用场合。

1 共模电压产生原理

本节对PMSM驱动系统的共模电压进行分析，两电平三相电压源逆变器(2L-VSI)驱动系统结构如图1所示，其中，Udc为直流母线电压，n为电机定子绕组中性点，Uno为中性点和直流侧中点之间的电压。

共模电压定义为电机定子绕组中性点n和接地点g之间的电压差Ung，表达式如下：

(1)

图1中Sa、Sb、Sc为驱动PMSM的三相两电平逆变器开关状态，值为1或0，“1”表示逆变器上桥臂导通，下桥臂关断;“0”表示逆变器的上桥臂关断，下桥臂导通。对于两电平逆变器，共有8种逆变器开关状态，对应电压矢量U0～U7。表1为各电压矢量与其对应的共模电压幅值，可见零电压矢量的使用是造成较大共模电压的原因，为抑制共模电压，应避免使用U0和U7这2个零电压矢量。

图1 2L-VSI驱动系统结构

表1 各电压矢量对应的共模电压幅值

2 PMSM转矩预测模型

在αβ静止坐标系下，表贴式PMSM的电压方程表示如下：

(2)

式中:uα、uβ为定子电压us的αβ轴分量;R为定子电阻;iα、iβ为定子电流的αβ轴分量;ψα、ψβ为定子磁链ψs的αβ轴分量。

采用前向欧拉法对定子磁链导数进行离散化，整理可得：

(3)

式中:Ts为控制周期;k为当前时刻;k+1为下一时刻。

则电磁转矩的预测值为

(4)

根据定子磁链和定子电流的关系，可得定子电流的预测值表达式如下：

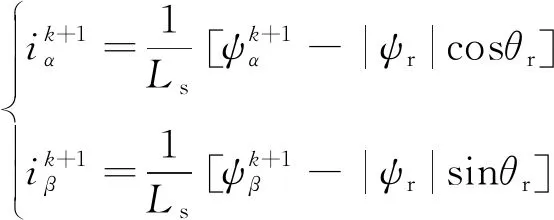
(5)

式中:ψr为永磁磁链;Ls为定子电感;θr为电机转子位置角，即永磁磁链与α轴之间的夹角。

电磁转矩Te的方程如下：

Te=1.5p(ψαiβ-ψβiα)

(6)

式中：p为电机极对数。

根据式(7)可得电机电磁转矩的预测值，表达式如下：

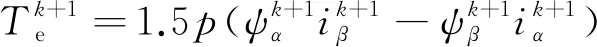
(7)

3 混合MPTC策略

本文针对共模电压抑制方法难以兼顾开关频率和转矩性能的问题，提出一种混合MPTC策略，通过切换使用虚拟矢量和多矢量合成2种电压矢量生成方式，只需较低的平均开关频率即可抑制共模电压，同时实现较好的转矩静、动态控制性能。

3.1 参考电压矢量计算

无差拍控制是一种在一个控制周期内使被控量达到期望值的离散控制技术[20]，本节以表贴式PMSM为例，基于无差拍控制思想计算参考电压矢量，在此基础上实现MPTC。PMSM的定子磁链表达式如下：

(8)

式中：θs为定子磁链位置角。

静止坐标系下的角度关系如图2所示，有角度关系为

图2 静止坐标系下的角度关系

θs=θr+δ

(9)

式中：δ为转矩角，即定子磁链和转子磁链之间的夹角。

(10)

表贴式PMSM的电磁转矩可表示为

(11)

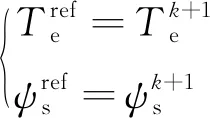
(12)

又因电磁转矩、定子磁链幅值和转矩角δ之间满足式(11)的关系，从而可得给定转矩角δref表达式：

(13)

(14)

3.2 电压矢量生成方式对比分析

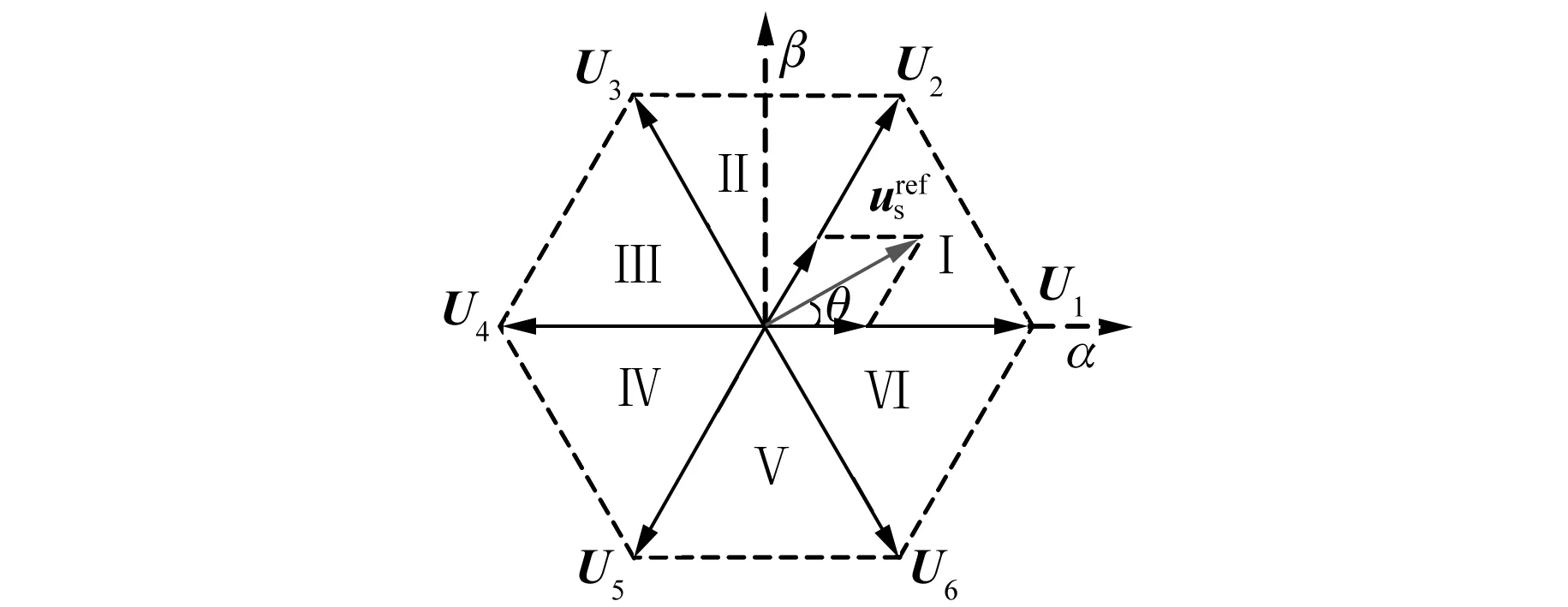
图3 参考电压矢量合成

同样以扇区Ⅰ为例介绍各矢量作用时间表达式。定义矢量U1的作用时间为T1，矢量U2的作用时间为T2，矢量U6和U3用作等效零矢量，两者的作用时间T3、T4相等，为零矢量作用时间T0的一半。由几何关系可得：

(15)

式中：θ为参考电压矢量和α轴之间的夹角。

|U1|=|U2|=2Udc/3，代入式(15)整理可得作用时间如下：

(16)

基于等效零矢量的多矢量合成法在有效抑制共模电压的同时，也具有良好的转矩性能，但是此法在单个控制周期内开关次数均为3次，其开关频率较高。

为降低开关频率，可选用虚拟矢量法作为电压矢量的生成方式，其原理如下：

摒弃使用零电压矢量后，采用6个非零基本电压矢量合成虚拟矢量加入控制集，得到矢量分布如图4所示。

图4 包含虚拟矢量的控制集

控制集包括6个非零基本电压矢量U1～6和6个虚拟矢量U12，U23,…,U61，其中虚拟矢量由每个扇区的2个边界有效矢量各作用0.5个控制周期来合成，表达式如下:

TsUij=0.5Ts(Ui+Uj),i,j=1,2,…,6

(17)

在上述控制集中通过价值函数J筛选出最优的作用矢量。价值函数定义为如下形式：

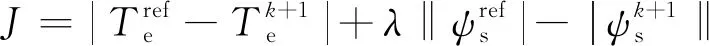
(18)

式中：λ为权重系数。

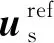
使用上述的虚拟矢量法，在单个控制周期内开关次数均为1次，开关频率比前述四矢量合成法明显降低，但其本质上只是参考电压矢量的近似，而无法精确地合成参考电压矢量，故其转矩性能有所降低。

3.3 电压矢量生成方式的切换规则

图5 不同参考矢量幅值时生成方法对比

表2 2种电压矢量生成方法对比

综上，提出混合MPTC方法的结构框图，如图6所示。

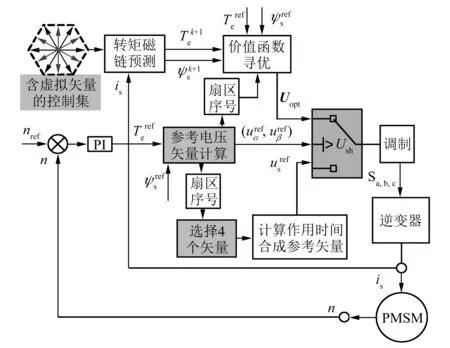
图6 混合MPTC结构框图

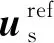
3.4 矢量作用顺序

为了减小控制周内逆变器的开关频率，降低开关损耗，需对混合MPTC的矢量作用顺序进行合理的安排，遵循的原则为每次改变开关状态时，只改变一相的状态。2种电压矢量生成方式的矢量作用顺序如图7所示。

图7 矢量作用顺序

对于虚拟矢量法，虚拟矢量由相邻的2个非零基本电压矢量各作用一半的控制周期来合成，作用顺序按照对称三段式，即Ui-Ui+1-Ui的顺序，以虚拟矢量U12为例，矢量U1和U2的作用顺序如图7(a)所示。对于多矢量合成法，采用4个非零电压矢量合成参考矢量，因而作用顺序为对称七段式，即Ui-1-Ui-Ui+1-Ui+2的顺序，以扇区Ⅰ为例，矢量U6、U1、U2和U3的作用顺序如图7(b)所示。

4 仿真验证

基于MATLAB/Simulink平台搭建了表贴式PMSM MPTC模型，对本文方法的共模电压抑制能力、转矩性能、开关频率和对其的折中能力，以及参数鲁棒性进行仿真验证。采用离散仿真模型，控制周期50 μs，直流母线电压24 V，仿真时长1 s，表3为仿真用电机的主要参数。

表3 表贴式PMSM主要参数

为验证混合MPTC的共模电压抑制能力，对本文方法与传统MPTC进行对比仿真。为了更好地表现本文方法切换的性质，根据基本电压矢量的幅值2Udc/3，设定切换阈值Ush为Udc/3，即8 V，令电机转速在1 s内从0匀速增长到140 r/min，负载转矩为1 N·m，共模电压对比如图8所示，其中图8(a)为传统MPTC的共模电压及其在0.050～0.051 s之间的放大图，由于传统方法使用了零电压矢量，因而存在幅值为±Udc/2的共模电压，即±12 V，与仿真结果对应。图8(b)为本文方法的共模电压及其放大图，图8(b)左侧为多矢量合成法的运行阶段，而图8(b)右侧为虚拟矢量法的运行阶段，可见共模电压幅值最高为±Udc/6，即±4 V，故验证了本文方法能够有效地抑制共模电压。

图8 共模电压对比

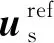
(19)

式中：m为系样点的个数。

由图9可见，当混合MPTC切换为多矢量合成法时，稳态转矩脉动为0.032 7 N·m，当切换为虚拟矢量法时，稳态转矩脉动为0.059 5 N·m，均小于传统MPTC 0.107 N·m的转矩脉动，稳态转矩性能良好。并且本文方法在约0.5 ms后达到给定转矩值，与传统MPTC相等，转矩阶跃动态响应快，且无超调。

图9 转矩阶跃仿真对比

为验证混合MPTC降低开关频率的能力，对本文方法和文献[19]中的多矢量合成法进行对比。切换阈值Ush仍设为8 V，负载转矩为2 N·m，给定正弦变化的转速，周期为0.1 s，幅值从0～140 r/min，图10为多矢量合成法和本文方法的电磁转矩对比图，多矢量合成法的转矩脉动为0.028 6 N·m，而本文方法的转矩脉动为0.043 2 N·m。图11为两者开关频率对比图，多矢量合成法的平均开关频率为20 kHz，而本文方法的平均开关频率为14.69 kHz。综上，与多矢量合成法相比，本文方法的转矩脉动有所增大，但平均开关频率明显降低。

图10 电磁转矩对比

图11 开关频率对比

图12 转矩脉动和开关频率变化规律

此外，由于MPTC依赖被控对象准确的模型和参数，对其鲁棒性的研究也非常重要，对于PMSM，MPTC所需的主要参数为电机的定子电阻、定子电感以及永磁磁链，文献[21]对常用MPC策略的参数鲁棒性进行了较细致的研究，由于篇幅限制，不再赘述，在此只对本文方法的参数鲁棒性进行验证。令上述主要参数存在10%的误差，仿真工况同图12，切换阈值Ush仍设为8 V，得到电磁转矩波形，并与无参数误差的波形进行对比，如图13所示。可见无参数误差时，平均转矩脉动为0.044 7 N·m，而存在10%参数误差时，平均转矩脉动增大为0.128 N·m，虽然性能有所下降，但系统仍能够正常运行，参数鲁棒性得以验证。

图13 存在参数误差时电磁转矩对比

5 结 语

本文提出了一种具有共模电压抑制能力的混合MPTC策略，针对不同幅值的参考电压，混合使用虚拟矢量和多矢量合成2种电压矢量生成方式，摒弃零矢量以抑制共模电压，在保证转矩控制性能的同时降低平均开关频率。通过改变矢量生成方式的切换条件实现开关频率和转矩脉动的灵活折中。仿真结果表明，所提方法可有效抑制共模电压，保留了常规MPC的动态性能优势，并兼顾保证了较低的开关频率和转矩脉动。