考虑用户边际成本偏好的逐日交通路径选择模型

张文义，张 璇，何彦博，马继辉

（北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室,北京 100044）

现实交通网络时常因受到不良天气、交通事故、道路施工、需求波动等因素干扰，处于非平衡态或向平衡态演化的过程.为描述交通网络的非平衡演化过程，继而提出合理有效的管理措施，研究超越现有平衡理论的非平衡分析方法尤为必要.逐日网络交通分配理论灵活性好，可将不同行为规则、集计水平和交通模式纳入统一框架进行分析，已成为描述网络交通流逐日非平衡演化过程的优选方法［1］.

逐日交通分配理论由Smith等［2-3］开创，基本任务是探究非平衡交通网络中出行者的逐日交通选择调整行为，及其促成的网络交通流逐日演化规律，还引发了逐日交通演化建模［4-7］、逐日交通选择行为实证［8-10］、逐日交通管理措施研究［11-13］和流量调整算法设计［14-16］等一系列研究方向.逐日交通演化模型可分为基于路径的模型和基于路段的模型.路径模型以路径流量演化为研究对象，路段模型则以路段流量演化为研究对象［4，17-19］.路段模型的提出者认为路径模型存在两个不足，一是路径流量难以辨识，二是路径重叠问题［4］.随着智能交通技术的发展，获取车辆行驶轨迹已变得简便经济，因此路径流量识别难的问题将不复存在.路径叠加是广泛存在于现实路网中的一种物理现象，不应将其视为路径模型的固有不足，可通过研究并揭示路径叠加对于微观个体逐日交通选择行为的影响机理来解决这一问题.事实上，路径模型比路段模型在出行行为研究上更具有基础性优势，因为微观个体出行决策的直接载体是路径而非路段，路段流量的演化是路径流量演化的次生结果.路径模型可对各种微观个体行为偏好进行直接建模，较之路段模型具有更加全面和根本的行为刻画能力和解释能力.综上，逐日交通选择行为研究将基于路径的确定型逐日交通演化模型进行.Yang等［20］对单引力流、网络纠错过程、投影动力系统、BNN 调整过程和比例调整过程（Proportionalswitch Adjustment Process，PAP）5 类基于路径的确定型逐日交通演化模型进行了总结分析，发现5 类模型均为理性行为调整过程，其中PAP 的数学结构和行为解释最为简单直观.一些学者基于PAP 进行了深入研究，Cho等［21］在其基础上建立了刺激-反应模型；Mounce等［22］在PAP 框架下探讨了不同费用指数和备选路径集下路径选择调整过程的稳定性；Zhang等［23］提出了一个PAP 的非线性改进模型，可避免流量的过度调整，并被进一步拓展至绝对和相对有限理性情形［24］.Xiao等［25］将路网流量演化过程视为带阻尼的弹簧系统，并据此建立了相应的动力学模型.与前述研究不同，Kumar等［26］在建立的路径调整模型中考虑了备选路径费用灵敏度的影响，该费用灵敏度可被理解为经济学中的边际成本［19］.近年来，逐日交通路径调整行为的建模主要侧重于在已有研究框架内进一步考虑社交影响、风险偏好、交通信息等因素的影响［27-30］.

现有研究中，包括PAP 在内的逐日交通路径调整模型大都假设出行者只关注路径调整带来的收益，该假设一定程度违背了经济学中的边际决策理论［31］.根据该理论，人们在进行边际决策时不仅关注边际收益，还会考虑边际成本.交通出行者的路径调整行为实际上也可视为一种边际决策，因此出行者不应只关心调至备选路径可获得的边际收益（即旅行时间节约），还应考虑调至该路径所导致的边际成本（即旅行时间增加），然而现有研究一般只关注前者，却忽略了后者.文献［26］虽考虑了边际成本的影响，但提出的边际成本计算方法未考虑路径叠加的影响.

综上，本文提出一种可有效处置路径叠加现象的路径调整边际成本计算方法，并据此构建了考虑用户边际成本偏好（Marginal Cost Preference，MCP）的逐日交通路径调整模型，用来更加全面地刻画微观个体出行者的路径调整行为偏好，继而更准确地描述宏观路网的逐日交通演化过程.

1 边际成本偏好

现有的逐日交通演化模型中，理性行为调整规则［20］简单直观，已成为逐日交通调整行为建模的一项基本准则.然而，理性行为调整规则并不能完整概括出行个体的逐日交通调整行为偏好.逐日路径调整行为从出行者的角度可视为一种边际决策，出行个体当前路径与目标路径的正向旅行时间差值即为边际收益，由于个体单方面从当前路径调整至目标路径引发的目标路径旅行时间增量即为边际成本.对于旅行时间相等的两条备选路径，出行者在次日的调整决策中将更倾向于选择边际成本更小的路径，该类行为偏好即为边际成本偏好，实验也已观察到类似现象［9］.显然，理性行为调整规则尚无法涵盖边际成本偏好.本文将边际成本偏好定义为：给定当日旅行时长相等的两条备选路径，出行者在次日的路径调整决策时更可能选择边际成本更小的路径.

根据定义，旅行时长相等表明调至两条备选路径的边际收益相同，更小的边际成本表明可能带来更多的净收益，因此更有可能成为出行者次日调整的目标路径.在逐日交通调整行为中，次日路径调整的边际收益可定义为出行者前一天所用路径与次日的目标路径在前一天的旅行时间差值，由于差值为负不会触发路径调整，仅讨论旅行时间差值为正（即正向旅行时间差值）的情形；次日的路径调整边际成本则可定义为在前一天的交通条件下，由于出行者单方面从前一天所在路径调整至次日目标路径对目标路径所造成的潜在旅行时间增量.以图1 为例说明边际成本偏好及其对于路径调整行为的影响.图1 包含一个OD 对和3 条路径，其中路径1 上（20，4）表示路径1 的初始旅行时间为20，边际成本为4；路径2 的初始旅行时间为30，“N”表示边际成本未知；路径3 的初始旅行时间为20，边际成本为6.

图1 示例路网1Fig.1 Illustrative road network No.1

根据理性行为调整规则，出行者在次日只可能从路径2 向路径1 和路径3 调整，由于对应的边际收益均为10，因此出行者调整至路径1 和路径3 的概率相等.若进一步考虑边际成本的影响，结果将发生变化，路径2 上的出行个体在次日调整至路径1的可能性将大于路径3，该结果显然更符合预期，说明边际成本偏好可反映出行者更深层次的行为偏好.

为简化问题描述，图1 示例仅阐述了一次路径调整过程，且已知路径调整涉及的边际成本值.在研究实际问题时，需要依据新得到的交通状况对下一次路径调整涉及的边际成本进行循环更新，现有研究通过次日目标路径前一天的旅行时间对其流量求差分或偏导数来计算得到［26］.该计算方法简单，但并不适用于存在路径叠加的交通网络，通过图2 示例对此进行说明.图2 中的OD 对由路径1（即路段Ⅰ）、路径2（即路段Ⅱ→路段Ⅳ）和路径3（即路段Ⅲ→路段Ⅳ）相连，路段Ⅰ、Ⅱ、Ⅲ和Ⅳ的初始旅行时间分别为20、20、10 和10.

根据理性行为调整规则，流量将会从路径2 调至路径1 和3，由此假设路径1 和路径3 的边际成本均为5（根据现有方法［26］采取路段旅行时间对流量求导得到）.假设图2 中各路段的旅行时间可分离（即路段旅行时间只与本路段的流量有关），由于路径旅行时间和路段流量均满足可加性，进一步假设路段Ⅲ和路段Ⅳ分担的边际成本分别为2 和3.则路段Ⅰ、Ⅲ和Ⅳ的边际成本分别为5、2 和3；路段Ⅱ的边际成本未知.

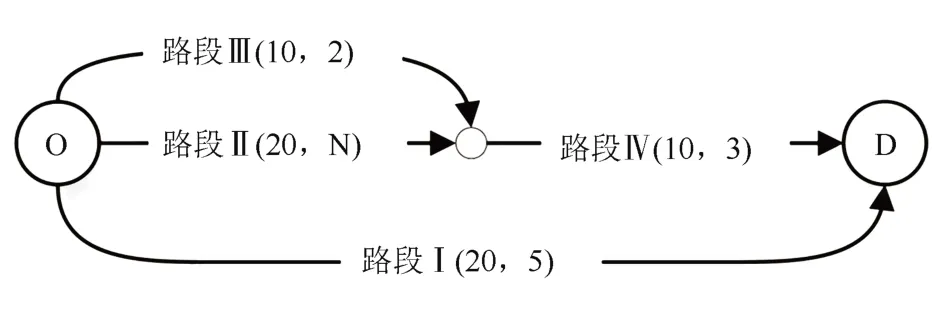
图2 示例路网2Fig.2 Illustrative road network No.2

基于上述设置可得出，路径2 上的流量调整至路径1 和路径3 的概率将相等.该结论并不合理，因为路径2 与路径3 共用路段Ⅳ，使得路径2 调整流量至路径3 并不会增加路段Ⅳ的旅行时间（因为路段Ⅳ的流量在调整前后没有变化），路径3 的旅行时间应该只增加2，而非现有方法计算得出的5.因此，路径2 上的出行者在次日的路径调整中更可能选择路径3，而非等概率地选择路径1 和3.示例路网2 说明现有的路径调整边际成本计算法方法并不合理，没有考虑路径重叠可能带来的影响.

由图2 示例可知，路径叠加会对路径调整过程中边际成本的计算产生实质影响，忽略路径叠加将导致边际成本的估计出现较大偏差，进而影响模型的准确性.此外，路径叠加有利于降低调整至与个体当前所在路径存在重叠路段的目标路径的边际成本，使得这些路径在调整过程中被选择的概率更大，可缓解路段模型指出的路径叠加问题［4］.

综上可得：考虑边际成本偏好与理性行为调整规则并不冲突，可丰富现有逐日交通出行选择行为理论；边际成本计算需考虑路网中普遍存在的路径叠加现象，否则将损害所建模型的可解释性和问题描述的准确度.因此，需要构建一个考虑路径叠加的路径调整边际成本计算方法，并结合逐日路径调整模型讨论边际成本偏好与理性行为调整规则的相容性.

2 逐日交通路径调整行为建模

逐日交通路径调整行为建模的目的是构建适用于路径叠加路网的路径调整边际成本计算方法，并将边际成本偏好合理纳入逐日路径调整行为模型中.PAP 模型虽然无法描述用户边际成本偏好，但其流量演化方程可为马尔科夫演化博弈提供良好的行为描述［32-33］.因此，基于PAP 的演化方程，通过构建一个可反映用户边际成本偏好的调整概率模型用来弥补PAP 的不足.有关边际成本和边际成本偏好的建模方法不仅适应于PAP，也可用于其他路径调整模型.

2.1 逐日路径调整模型

式（1）为流量演化方程，式（2）为微观个体的路径调整概率（或宏观路径流量调整比例）模型.式（1）表示调整前后路径的流量变化值等于调入该路径的流量与调出该路径的流量相减.由式（2）可知，下一时刻的流量调整只可能由同一OD 对间当前旅行时间更长的路径向时长更短的路径进行，并且流量调出比例随正向时长差增加而增大；同时，用户的反应强度与调至备选路径可能产生的边际成本反相关，且该边际成本受到调入和调出路径流量的共同影响.显然，令=0，边际成本偏好的影响将消失，模型将退化为原始的PAP.令路径旅行时间在定义域Ω上是非负、有界且连续可导的，式（2）中考虑路径叠加的边际成本计算方法为

由于旅行时间可加，故有

2.2 理论分析

从理论角度分析考虑用户边际成本偏好的逐日路径调整过程模型（Proportional-switch Adjustment Process with Net-Marginal Cost Preference，PAPNetMCP）的一些基本性质.为简化表述，将时间索引t隐去.

首先讨论PAP-NetMCP 的稳定态的特性.

1）命题1：PAP-NetMCP 的稳定态与用户均衡状态等价.

命题1 表明，考虑用户边际成本偏好以及边际成本的具体计算方式并不会改变流量调整的最终结果（即用户均衡），但可以预计它们将对路径选择和交通流演化过程产生的影响.然后，探讨PAPNetMCP 模型是否仍遵循理性行为调整规则.

2）命题2：PAP-NetMCP 是一个理性行为调整过程.

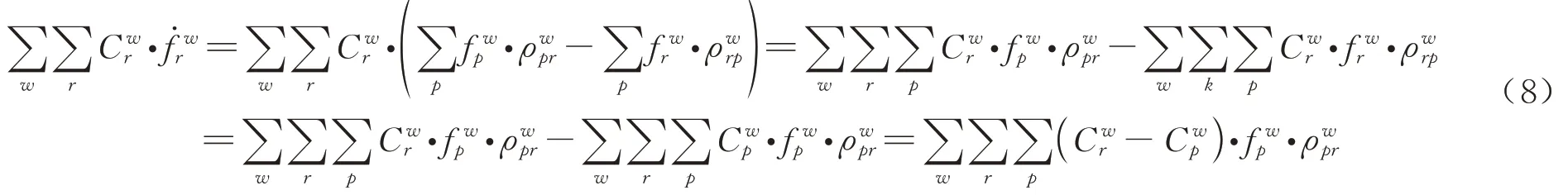
命题2 表明PAP-NetMCP 模型仍遵循理性行为调整规则，说明边际成本偏好与理性行为调整规则是相容的，可为逐日出行路径调整行为建模提供更完整的行为理论支持.

3 数值算例分析

通过数值灵敏度分析对理论分析未涉及的PAP-NetMCP 部分特性进行探讨.以交通分析中广泛应用的Braess 网络［35］作为算例网络.为简化描述，对网络参数和变量的单位予以省略.

3.1 Braess 网络

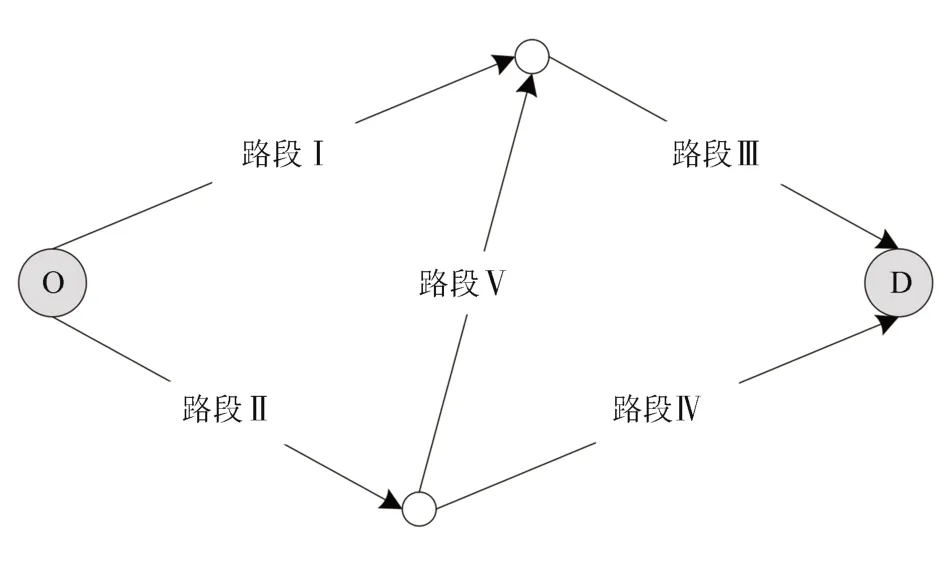
图3 Braess 网络Fig.3 Braess network

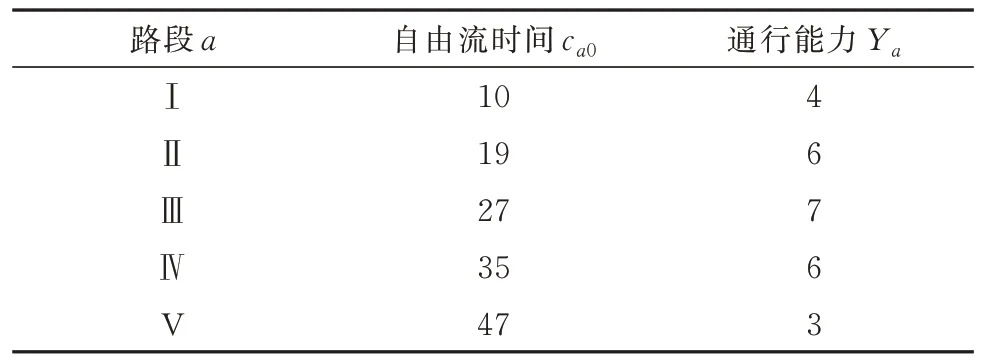
表1 路段旅行时间函数的参数取值Tab.1 Parameter values for travel time functions of each road

3.2 边际成本偏好强度分析

边际成本偏好强度分析是针对模型参数和进行对比性灵敏度分析，因只有1 个OD 对，省略上标w，令s0={0.002 5，0.005，0.01}且s1={0∶5∶15}.其中，s0分析序列的公比和s1分析序列的公差由前期试算得到，主要依据是对于当前规模的灵敏度分析，该组合下的参数序列带来的系统状态变化已可满足趋势变化分析的需要.

通过数值算例重点分析边际成本偏好强度s1对于网络交通流逐日演化过程与结果的影响.考虑到s0取不同值时网络交通流演化在不同s1条件下的变化趋势基本相似，故只给出s0=0.005 时不同s1对应的流量演化轨迹如图4 所示.

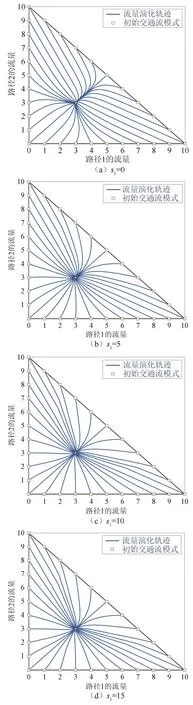
图4 s0=0.005 时不同s1下的交通流演化轨迹Fig.4 Traffic flow evolution trajectories under different s1 when s0=0.005

由图4（a）可知，当s1=0 时，不考虑用户边际成本偏好，此时模型退化为原始PAP，各流量演化轨迹的收敛方向呈现显著的不均匀性，基本上沿着3 个方向收敛至用户均衡点，致使部分演化轨迹的弯曲程度较大.相比之下，当s1＞0 时，流量演化轨迹收敛方向的不均匀性显著降低，由此使得流量演化轨迹的直线性明显增强.当s0=0.002 5和s0=0.01时，不同s1条件下的流量演化轨迹也呈现出与图4类似的变化趋势.实验结果表明：边际成本偏好对于网络交通流演化过程具有重要影响，不应被忽视；基于考虑边际成本偏好的逐日路径调整模型来开发交通分配算法（比如用于生成迭代方向），有望加快算法的收敛速度.通过图4 可知，当s1由5 增加至15时，演化轨迹的直线性有所增强，但增幅呈下降趋势.考虑到增加s1将使得反应强度下降，由此可能导致流量调整速度整体变慢，继而延缓网络演化至稳定态.因此，对调整模型进行算法开发时，s1取值不宜过大，且要能促成较好的轨迹直线性，实验中可将其设为10.

3.3 路径边际成本定义分析

路径边际成本定义分析主要探讨基于传统边际成本定义的路径调整模型（Proportional-switch Adjustment Process with Marginal Cost Preference，PAP-MCP）与PAP-NetMCP 对于网络交通流演化的不同影响.图5为s0=0.002 5和s0=0.005 时，不同s1取值下PAP-MCP 与PAP-NetMCP 这两种模型的交通流演化轨迹.

由图5 可知，基于不同边际成本定义的流量演化轨迹仍存在比较明显的差异.对于每个分图左上角（比如路径1 的流量小于3，路径2 的流量不小于7）和右下角（比如路径1 的流量不小于7，路径2 的流量小于3）的初始点，PAP-NetMCP 的流量演化轨迹的直线性明显强于PAP-MCP，说明相比于传统定义，考虑路径叠加的边际成本定义更有利于改善相应流量调整算法的性能.对比图5（a）、图5（c）、图5（e）和图5（b）、图5（d）、图5（f）可看出，s0取值一定时，随着s1的增加，流量演化轨迹的直线性变化趋势与图4 的观察结果基本一致；对比图5（a）和图5（b）、图5（c）和图5（d）、图5（e）和图5（f）可看出，s1取值一定时，随着s0的增加，流量演化轨迹的平滑性略有下降（可参见路径1 和路径2 的初始流量为（0，10）和（1，9）时对应的演化轨迹曲线），主要原因是s0的增加使得用户反应强度上升，可能导致单次流量调整的幅度加大，进而出现图中显示的弱乒乓式调整现象.

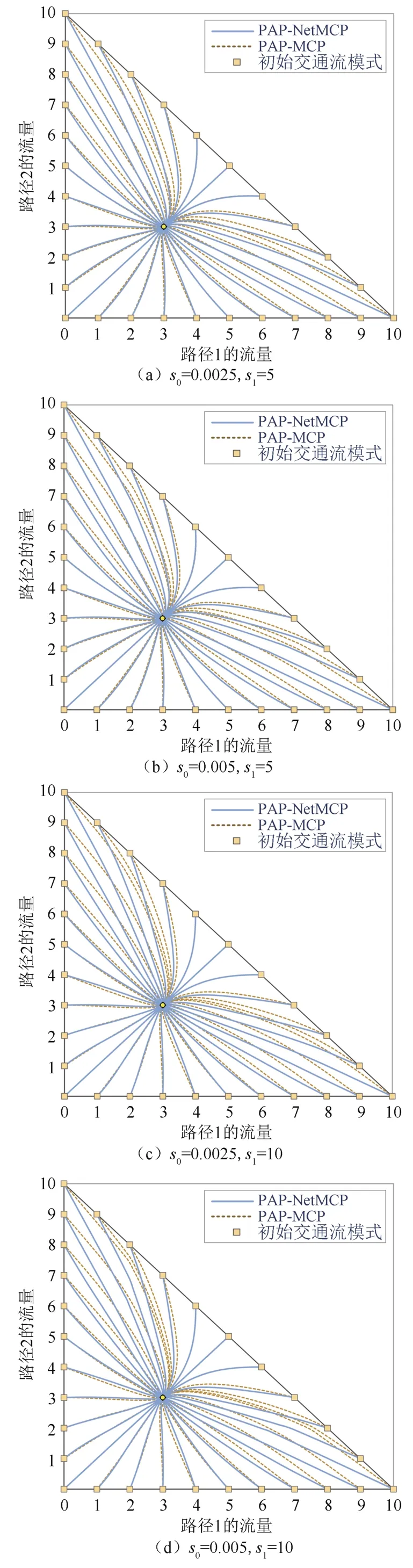
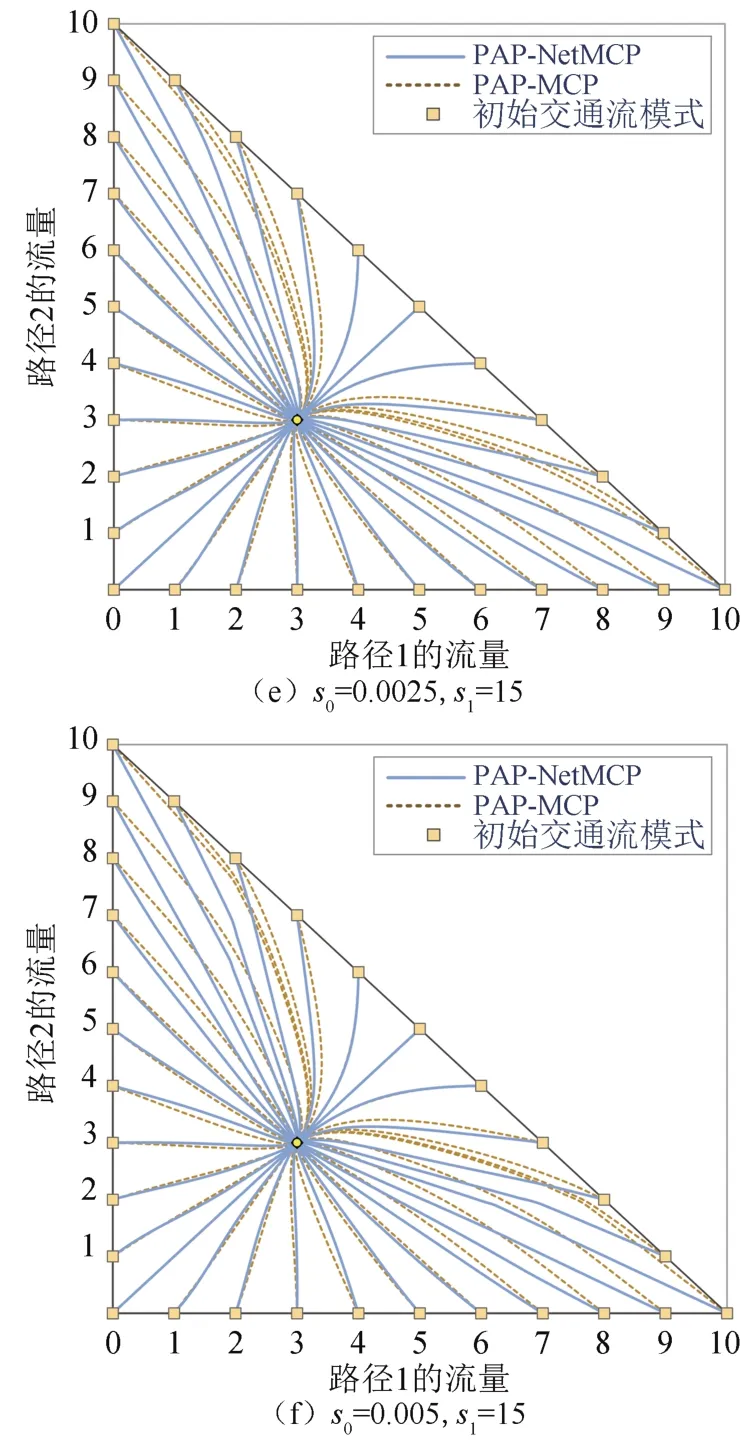
图5 不同s1下PAP-NetMCP 与PAP-MCP 的交通流演化轨迹Fig.5 Traffic flow evolution trajectories of PAP-NetMCP and PAP-MCP under different s1

4 结论

1）提出了一种适用于路径叠加网络的边际成本计算方法，并据此建立了考虑用户边际成本偏好的逐日交通路径调整模型PAP-NetMCP.

2）证明PAP-NetMCP 模型是一个理性行为调整过程，表明边际成本偏好与理性行为调整规则是相容的，丰富了现有逐日交通选择行为理论基础.

3）通过数值算例证明考虑用户边际成本偏好对于网络交通流演化过程的影响显著，后续研究不应忽视.

4）考虑路径重叠的边际成本计算方法有利于改善流量调整算法的性能，可使路径调整模型的流量演化轨迹长度更短，在此基础上开发确定型用户均衡的求解算法有望获得更好效果.