基于简化模型的铁路桥墩健康状态快速评估方法及应用研究

王冬立，战家旺，王闯

（1.国能朔黄铁路发展有限责任公司，河北 肃宁 062350；2.北京交通大学 土木建筑工程学院，北京 100044）

桥墩作为支撑上部梁体的重要构件，其工作状态直接影响整桥的安全性能.若桥墩状态不良，即使梁部结构状态很好，整个桥梁的使用性能也会受到影响［1］.铁路桥墩在使用期间不仅承受列车的动力荷载，还承受着流水冲刷、盐碱污水腐蚀、冻融循环以及突发的车船撞击等外力作用，因此容易出现各种各样的病害［2］.桥墩发生病害的部位一般在地面或者水面以下，难以简单地通过外观检查对其技术状态做出判断，也不易通过静力加载的方式进行评估.因此，桥墩健康状态的快速检测与评估是学术界和工程界关注的一个热点问题.

至今，已有部分学者针对桥墩健康评估方法进行了探究.李运生等［3］通过理论计算与实测数据分析，提出了基于综合指标的不同类型桥墩振幅的计算公式，对基于振幅的铁路桥墩的评估标准起到进一步深化作用.周海林等［4］研究了桩基参数对单桩横向刚度的影响，通过分析得到单桩横向刚度与桥墩自振频率的关系.陈兴冲［5］采用瑞利法推导出了适用于不同基础类型的桥墩基频的计算公式.冷伍明等［6］在群桩基础桥墩三维计算程序的基础上提出了正常状态下桥墩最低频率的参考值，可为群桩基础桥墩的评估研究提供一定的参考.战家旺等［7-8］基于冲击响应识别桥墩模态，然后以实测模态的不同组合为输入，采用模型修正技术和优化算法识别铁路简支梁桥下部结构的物理参数，从而建立对墩身、基础和支座病害进行定位和定量分析的动力学方法，并提出了针对下部结构系统中各构件的评估准则和评估流程.尹成斐［9］以朔黄重载铁路一水中桥墩为对象，分析在重载列车作用下的横桥向振幅，利用冲击振动试验法测试了横桥向自振频率，并依据规范初步判断桥墩整体健康状态.刘建磊等［10］通过桥墩原型试验对实际工程中的桥墩基础分阶段开展动刚度测试和静载试验，得到了桥墩-承台-桩基体系、承台-桩基体系和单桩的动刚度，并对桥墩的性能进行了评价.Mao等［11］采用模态分析和有限元模型修正技术，确定了某三跨简支梁桥桩基础沿深度方向的弹簧刚度及分布规律.李保龙［12］采用冲击振动试验法对一重载铁路多跨简支梁桥的自振频率进行了实际测量，根据Southwell 频率合成法和能量守恒原理推导了桥墩自振频率和基础刚度之间的关系.Davis等［13］提出了一种直接利用运营车辆激励下桥墩动应变和加速度响应来探测桥墩基础冲刷的方法.Ma等［14］利用动力瞬态响应法评估了重载铁路桥墩竖向动刚度，分析了列车引起的墩顶横、竖向振幅与动刚度间的关系，并采用支持向量机建立了二者关系的预测模型.

既有研究所提出的评估方法流程较为复杂，因此，本文根据文献［15］中提出的带有集中质量的单墩图式思路，以铁路多跨简支梁桥为研究对象，通过对梁体的振动特性进行分析，推导出多跨简支梁在外部激励作用下梁体等效集中质量的计算公式，进而将多跨简支梁简化为带有不同集中质量的简化模型.基于该简化模型提出一套多跨简支梁桥桥墩健康状态评估的新方法和相应的评估流程，并以南排河特大桥为试验对象，进一步说明了该方法在实际工程中的应用步骤.

1 多跨简支梁桥桥墩简化模型

首先，以铁路多跨简支梁中的一跨梁为研究对象.假设梁长为l，沿梁体纵向的分布质量为mˉ，梁体弹性模量为E，梁截面横向惯性矩为I，梁体左端和右端位置分别记为A 和B，EI为桥墩刚度.仅研究梁体横向振动，因此将桥墩竖向约束简化为固结，将桥墩、支座以及相邻梁跨的横向约束简化为相应的约束弹簧，其刚度分别为kA、kB，x、y、z分别代表桥梁顺桥向、横桥向和竖向.梁体的简化分析模型见图1.

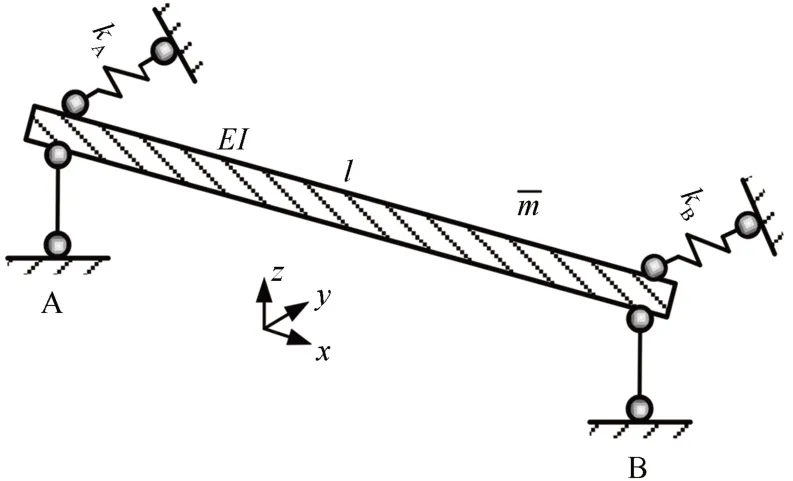
图1 梁体简化分析模型Fig.1 Simplified analysis model of beam

单跨简支梁梁体一阶振动时，其振型表现为半正弦曲线的形式，将梁体任一点x处的一阶振型幅值表示为

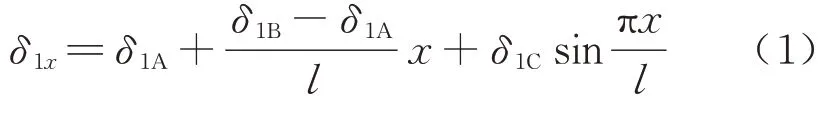
式中：δ1A，δ1B分别为梁体一阶振型下两梁端A 与B的振型幅值；δ1C为梁体跨中振型幅值.

对梁体的二阶振型函数作近似，将其二阶振型近似为直线，则梁体任一点x处的二阶振型幅值可以表示为

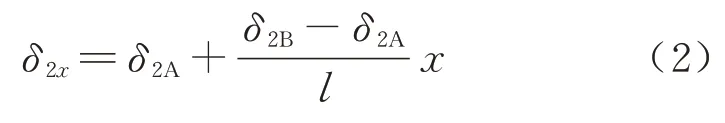
式中：δ2A，δ2B分别为二阶振型下梁端A 与B 的振型幅值.

单跨简支梁出现一阶振型时，将梁体质量等效为梁两端集中质量m1A、m1B及梁跨中的集中质量m1C；出现二阶振型时，将梁体质量等效为梁两端集中质量m2A、m2B，可由能量守恒原理分别计算前两阶梁体的振型等效集中质量为

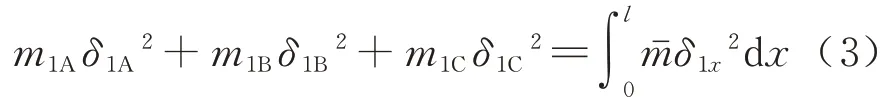
其中第一阶振型梁体等效的3 个集中质量时的振型幅值为

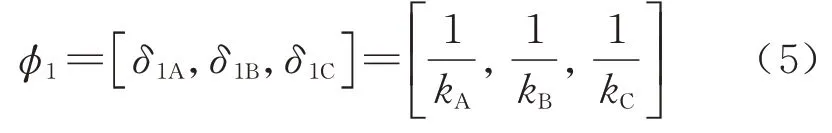
式中：kC为梁体刚度.

利用振型正交性进行整理，并考虑到墩梁刚度比较小的多跨简支梁中梁体弯曲程度δ1C较小，则可进一步得到

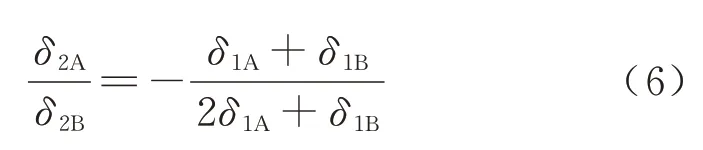
综合式（3）、式（5）和频率相等的条件可得到梁体一阶振型时两端的等效质量为

式中：α1A、α1B表示一阶振型时梁体在A 端、B 端的振型等效集中质量系数，即

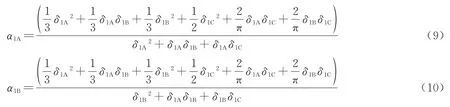
同理，综合式（4）、式（6）和频率相等的条件可得梁体二阶振型时两端的等效质量为

式中：α2A、α2B表示二阶振型时梁体在A 端、B 端的振型等效集中质量系数，即

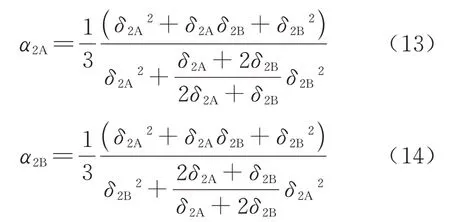
综上所述，对简支梁出现的一阶振型，可以根据式（7）和式（8）将梁体质量等效为梁体两端的集中质量；对于单跨简支梁出现二阶振型时，采用式（11）和式（12）对梁体质量进行等效.

在单跨简支梁梁体振型等效集中质量的计算方法基础上，进一步进行多跨简支梁梁体振型等效集中质量计算方法探究.取多跨简支梁某一桥墩为中心墩，在低阶频率时可将左右梁体的质量作如图2所示的4 种情况进行等效.图2 中，第1 种振型为中心墩相邻两侧梁体的梁端为同向振动，第2 种振型为中心墩左侧梁体的梁端为异向振动，右侧梁体的梁端同向振动，第3 种振型为中心墩左侧梁体的梁端为同向振动，右侧梁体的梁端异向振动，第4 种振型为中心墩左、右两侧梁体的梁端均为异向振动.对于不同情况下梁体振型等效集中质量均可按单跨简支梁梁体对应的公式计算.m1A、m2A分别表示中心墩左侧梁体在一阶、二阶振型下的梁端等效集中质量，m1C、m1D分别表示中心墩左侧、右侧梁体一阶振型下的梁体跨中等效集中质量，m1E、m2E分别表示中心墩右侧梁体在一阶、二阶振型下的梁端等效集中质量.

图2 不同振型的梁体振型等效集中质量示意图Fig.2 Schematic diagram of equivalent concentrated mass of beam under different vibration patterns

对于不同振型情况下中心墩墩顶振型等效集中质量m可统一表示为

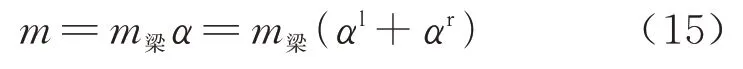
式中：m梁表示一跨梁体的质量；αl为左侧梁体靠近中心墩一端的振型等效集中质量系数；αr为右侧梁体靠近中心墩一端的振型等效集中质量系数；α表示中心墩墩顶振型等效集中质量系数.

求出墩顶振型等效集中质量之后，多跨简支梁体系横桥向振动即可简化为如图3 所示的简化模型，基底约束参考文献［16］等效为具有相应刚度的弹簧约束，其中khy为横桥向平动弹簧、krx为横桥向转动的扭转弹簧，kz为竖向平动弹簧.

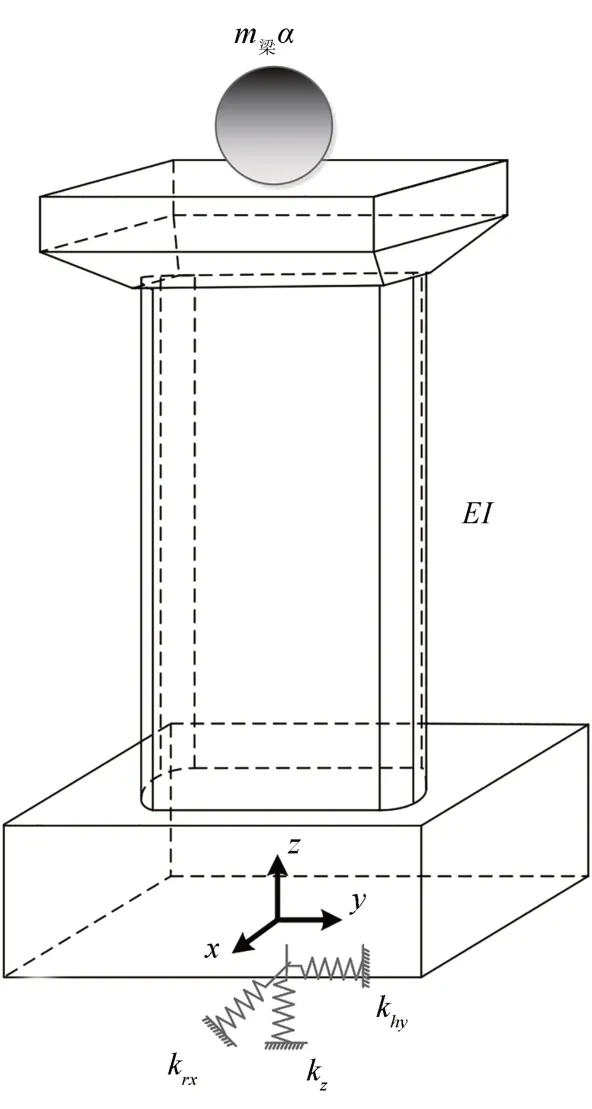
图3 多跨简支梁桥简化模型Fig.3 Simplified model of multi-span simply-supported beam bridge

2 桥墩健康状态快速评估方法

2.1 评估指标

基于提出的多跨简支梁桥墩简化模型，利用模型修正理论识别桥墩细部参数，根据识别出的参数提出桥墩健康状态评估指标和相应的评估准则.首先以待测桥墩的实测低阶频率fi及相应的桥墩振型［φj］为目标值，以简化模型的理论频率f'i和振型［φ'j］，建立模型修正理论中的目标函数为

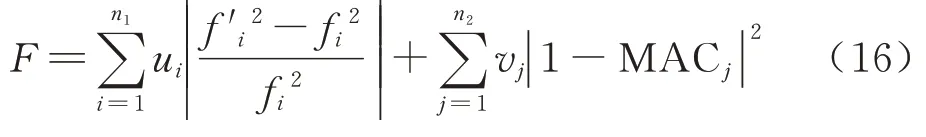
式中：ui和vj分别为频率和振型的权重系数；n1和n2分别为采用的模态频率阶数和模态振型阶数；MACj表示第j阶理论振型与实测振型的模态振型相似度指数，其值介于0 到1 之间，计算公式为

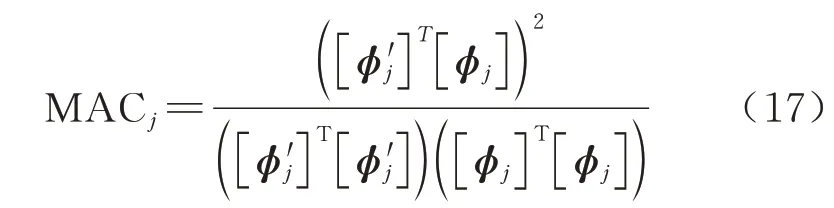
建立目标函数之后，找出最优解识别出桥墩结构细部参数，最终使目标函数满足的收敛准则为

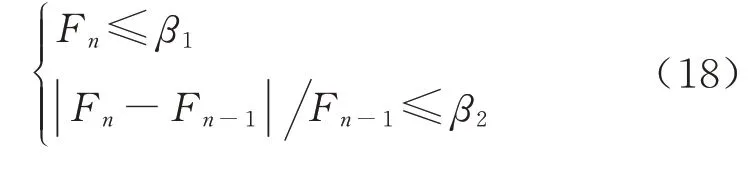
式中：n为迭代数；β1为容许误差，β2为容许残差.

冲刷和腐蚀条件下桥墩健康状态评估可从桥梁构件性能和整体性能两方面研究.

1）局部状态评估指标.

桥墩墩身腐蚀通过墩身截面惯性矩I的下降来评估，由此定义了墩身局部健康状态评估指数θp为

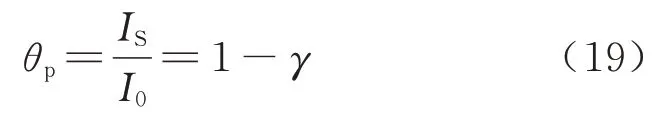
式中：γ桥墩病害指数；IS为墩身惯性矩的识别值；I0为墩身惯性矩的初始值.初始值可选取一定数量的健康桥墩为试验对象，结合大量的实测数据，进而求得惯性矩的标准值，也可采用设计值截面的惯性矩计算值作为标准值.参考文献［17］建立表1 所示的墩身性能劣化评估准则.

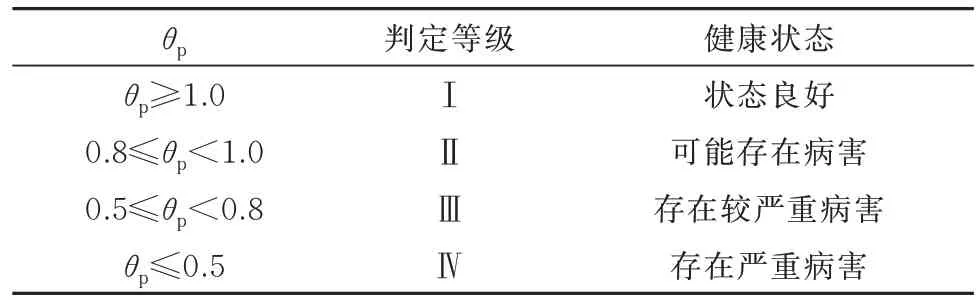
表1 腐蚀病害评估建议准则Tab.1 Recommended criteria for corrosion disease assessment

基础冲刷病害的评估指标定义为基底约束刚度识别值与基础刚度基准值的比值：基础减弱引起基底的等效弹簧刚度值下降，由此实现对铁路桥梁水中桥墩病害的定量表征.定义基础冲刷状态指数θf为

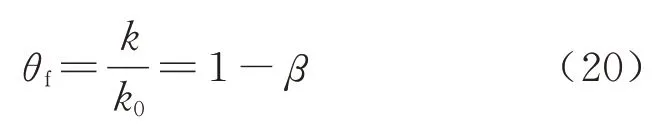
式中：k0表示基础未发生病害时等效弹簧刚度的初始值；k表示基础发生病害后等效弹簧刚度值；β为基础病害指数.在参数识别时一般仅把对桥墩系统影响较大的转动弹簧krx作为待识别变量，横向水平弹簧刚度khy同时发生等比例的刚度折减.

从评估角度考虑，建议设计单位在设计文件中指定下部结构纵向线刚度的同时，给出基础约束刚度计算值，以免评估时计算值出现偏差.考虑到基础设计时候安全系数一般取2.0，提出了表2 所示的桥梁基础冲刷评估建议准则.

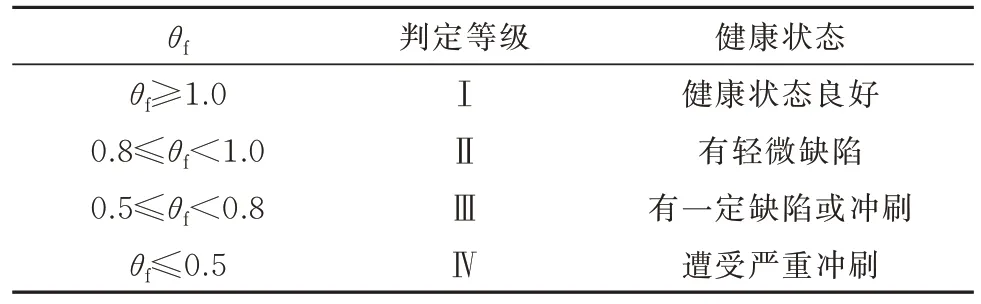
表2 冲刷病害评估建议准则Tab.2 Recommended criteria for scour disease assessment

2）整体状态评估指标.

用横向自振频率指标对桥墩整体工作状态进行评价.桥墩健全度指数（Soundness Index，SI）定义为

式中：fe和fd分别为桥墩自振频率实测值和基准值.

桥墩基阶频率较高时，采用式（21）所示指标对桥墩整体状态进行评估，当墩梁耦合较强，且桥墩频率较低时，病害引起的桥墩频率变化率较低，不宜采用该指标进行评估.故定义基于线刚度的桥墩整体健康状态评估指标纵向线刚度指数（Linear Stiffness Index，LSI）为

式中：Si和Sd分别为桥墩纵向线刚度识别值和基准值.

式（22）中线刚度识别值指数为根据实测桥墩的模态信息识别出的桥墩细部参数进而求得桥墩线刚度识别值.在公路桥梁技术状态等级评定标准的基础上，提出基于线刚度指数的桥墩整体健康状态评估准则如表3 所示.

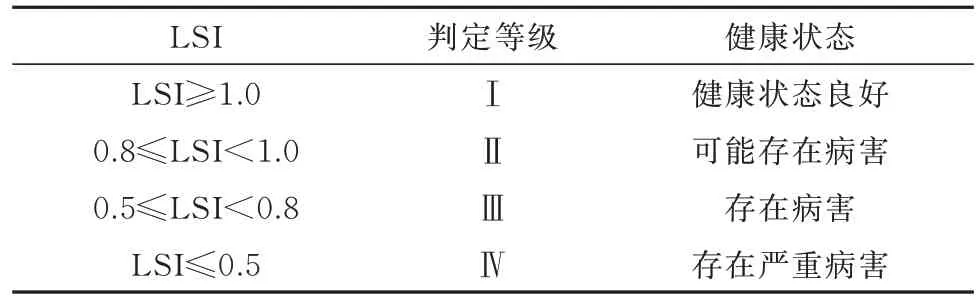
表3 桥墩整体健康状态评估建议准则Tab.3 Recommended criteria for pier overall health assessment

2.2 评估流程

对铁路多跨简支梁桥桥墩健康状态评估时，首先通过频率指标初步判断桥墩的健康状态，其次求得待测桥墩的墩顶振型等效集中质量，得到相应的简化模型，利用模型修正和优化算法理论识别待测桥墩的细部参数，根据提出的健康状态评估指标和评估准则即可完成多跨简支梁桥桥墩健康状态的定量评估.以一多跨简支桥梁为例（共9 个桥墩，标记为1 号～9 号），具体评估流程分为4 个步骤.

步骤1：假设选取3 号墩为待测桥墩，在其左侧3号梁体的梁端及跨中布置1#、2#、3#横向传感器，在其右侧4 号梁体的梁端及跨中布置4#、5#、6#横桥向传感器，3 号墩的墩顶、墩中、墩底布置测点布置7#、8#、9#横桥向传感器，测点布置完成后对3 号桥墩墩顶施加横桥向的锤击力，拾取各测点的时程响应.

步骤2：对各测点的响应进行频谱分析、振型分析，分别得到各测点的振型幅值，对应频率f1、f2时相邻两侧梁体的横桥向振型为图2 所示4 种振型中的一种，对于任何一种振型均可按提出的梁体振型等效集中质量的计算公式得到3 号墩墩顶振型等效集中质量.

步骤3：依据多跨简支梁简化原则，即可得到与3 号墩相应的多跨简支梁简化模型，且将实测频率f1、f2定为该简化模型的实测频率，通过拾取3 号墩墩顶、墩中、墩底布置的7#、8#、9#测点时程响应频谱分析可得3 号墩的实测振型.建立基于桥墩自振频率和振型的目标函数以及3 号墩的有限元模型，以实测频率和振型为目标，以3 号墩墩身惯性矩和基础约束刚度为待识别参数，通过模型修正识别出3 号墩细部参数.

步骤4：基于识别的参数，根据提出的桥墩健康状态整体和局部评估指标，同时参照表1～表3 的评估准则对3 号墩的健康状态进行分级评定.

3 试验探究

为验证提出的评估方法在实际工程中的可行性并更直观地说明其应用步骤，以南排河特大桥（图4）为试验对象，选取水中4 号墩、5 号墩为待测中心墩进行试验探究.

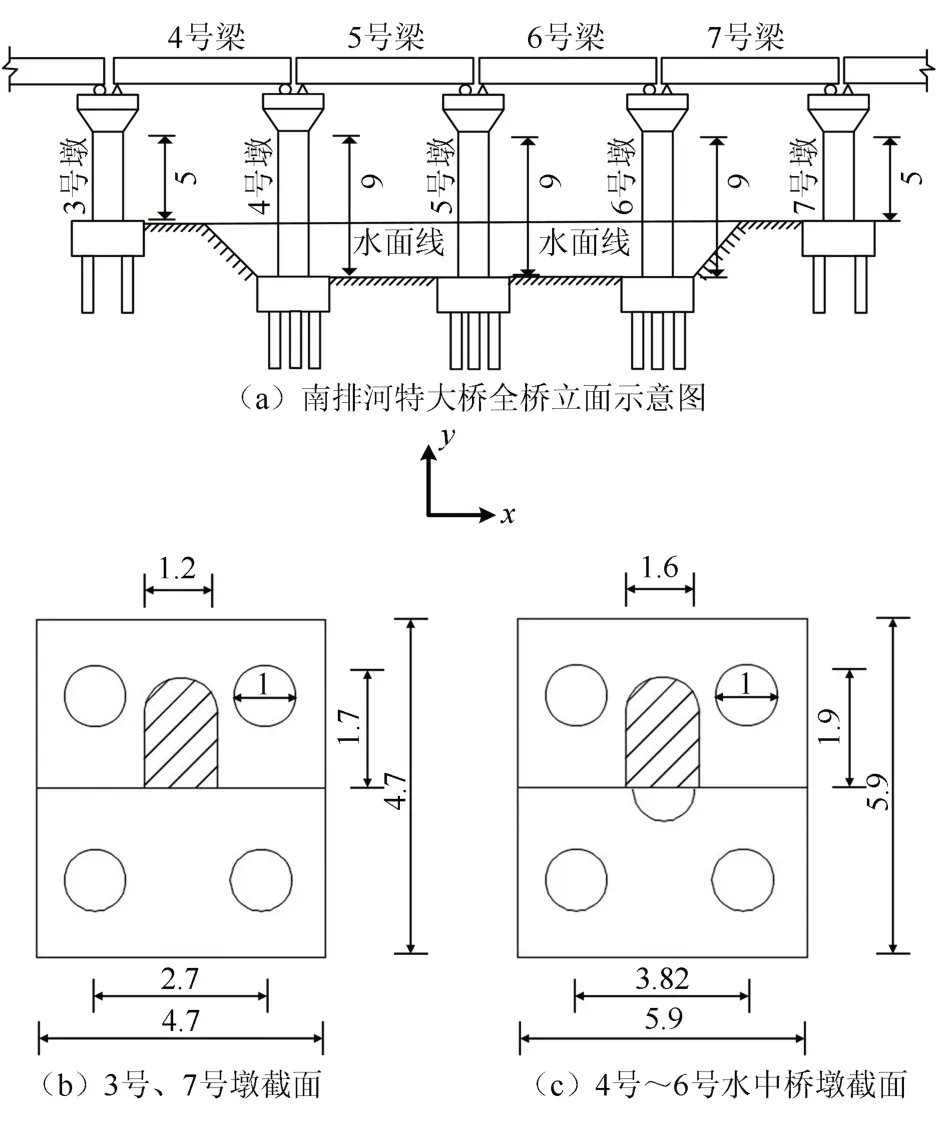
图4 南排河特大桥示意图（单位：m）Fig.4 Schematic diagram of Nanpai River bridge (unit:m)

3.1 试验方案

3.1.1 测点布置形式

步骤1：以4 号墩为待测中心墩，分别在4 号墩墩顶、距墩顶6.05 m（记为墩中测点）、7.25 m（记为墩底测点）处布置3 个测点，在4 号梁、5 号梁梁顶的两端及跨中各布置3 个测点，测点布置图见图5.

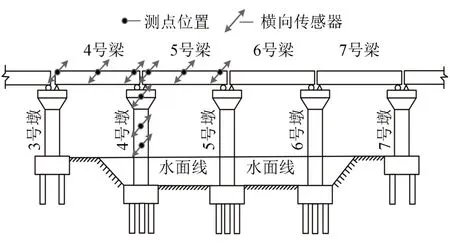
图5 4 号墩测点布置图Fig.5 Layout of measuring points at pier No.4

步骤2：以5 号墩为待测中心墩，分别在5 号墩墩顶、距墩顶6.08 m（记为墩中测点）、7.33 m（记为墩底测点）处布置3 个测点，在5 号梁、6 号梁梁顶的梁端及跨中各布置3 个测点，测点布置图见图6.

3.1.2 现场试验

本次试验激励采用冲击荷载，现场的试验情况如图7 所示，采用的激励装置为30 kg 的特制重锤，包裹一圈橡胶，用来保护梁体在重锤的撞击下不致被破坏，且该特制重锤所施加的冲击荷载为白噪声荷载，故采用该铁球作冲击力时，可不考虑冲击荷载的频谱特性，仅需对结构响应作频谱分析即可得到相应的频率值.试验工况设置为：工况1 加载方式为锤击4 号墩顶，工况2 加载方式为环境激励，二者测点布置如图5 所示；工况3 加载方式为锤击5 号墩顶，工况4 加载方式为环境激励，二者测点布置如图6所示.

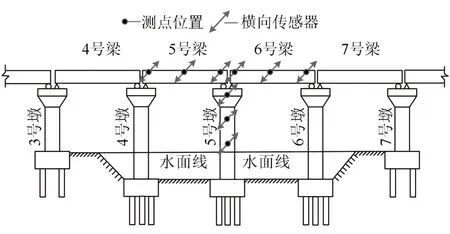
图6 5 号墩测点布置图Fig.6 Layout of measuring points at pier No.5

图7 现场试验概况Fig.7 Field test overview

3.2 桥墩健康状态评估

3.2.1 时程分析

通过多次锤击，提取各测点的响应，由于测点比较多，仅列出工况1（锤击试验）、工况4（环境激励试验）各2 个测点的时程响应如图8 所示，通过时程信号可知，锤击激励均能激起各测点的响应，且均有明显的衰减，脉动试验也能采集到明显的信号.

3.2.2 频谱分析

对图8 测点的时程响应作频谱分析，结果如图9所示，对工况1、工况2 测点信号进行频谱分析可得到首峰频率为2.25 Hz，该频率为以4 号墩为中心的区域频率.对工况3、工况4 的测点信号进行频谱分析可得首峰频率同样为2.25 Hz，说明以5 号墩为中心的区域频率也为2.25 Hz，同时也说明2.25 Hz 是4号墩、5 号墩附近的区域频率.

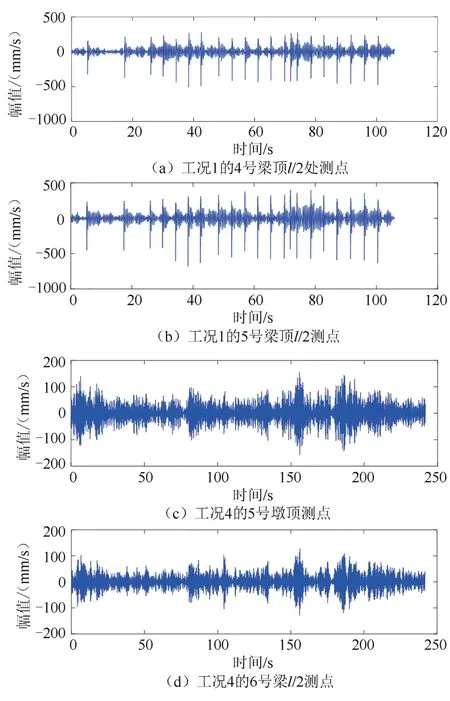
图8 测点速度响应时程图Fig.8 Velocity response time history diagram of measuring points

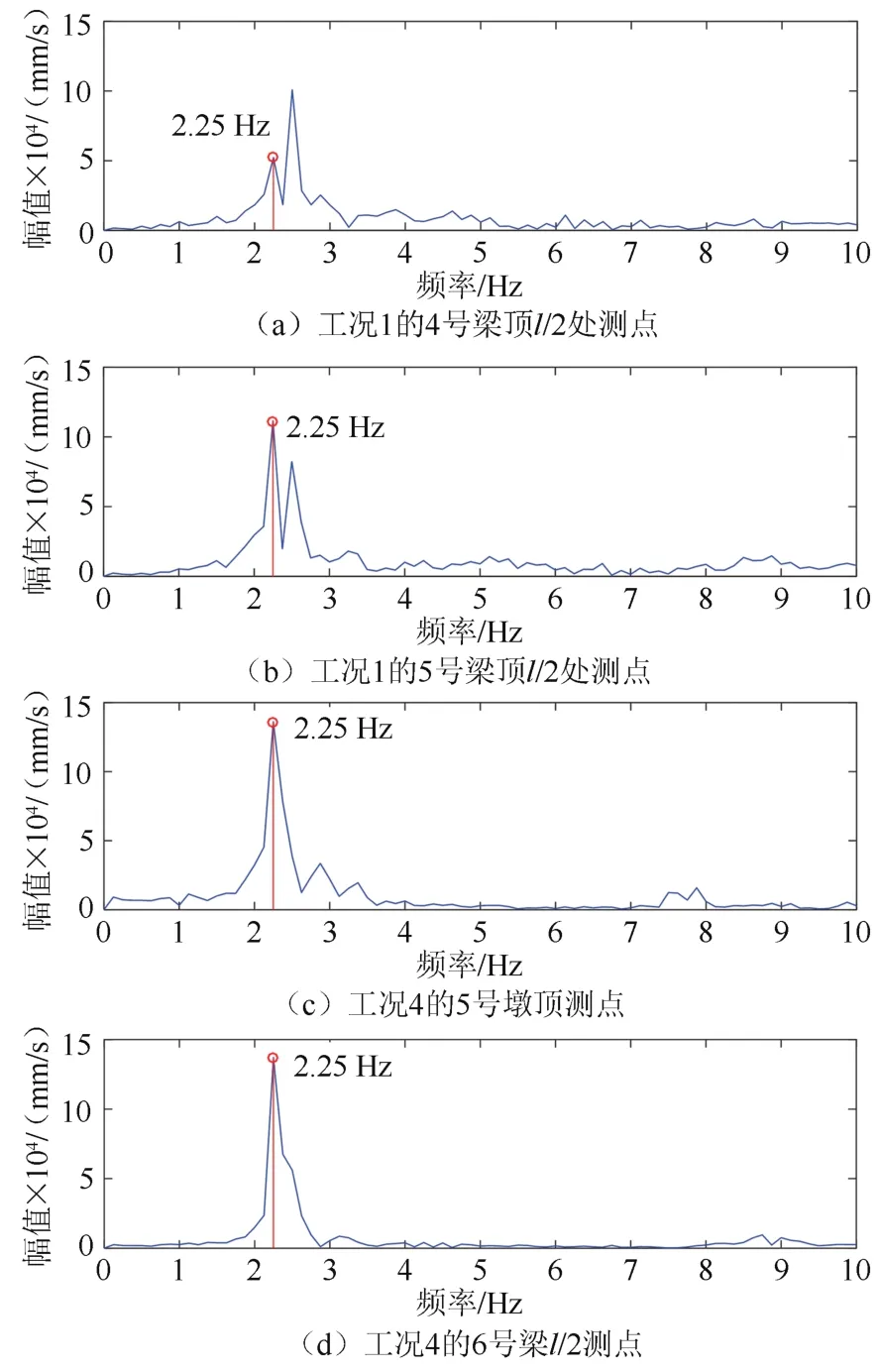
图9 测点响应频谱图Fig.9 Response spectrum of measuring points

3.2.3 振型分析

以工况1 为例，对各测点进行自谱和互谱分析，以4 号梁顶测点l/2 处的振型幅值为参考点，做出与首峰频率2.25 Hz 对应的4 号梁、5 号梁振型如图10所示，可以看到4 号墩左右两侧梁体的振型均为同向振动，满足提出的首峰频率的条件即待测桥墩左右两侧梁体梁端的振型均为同侧振动，故可利用首峰频率作为4 号桥墩参数识别的依据.

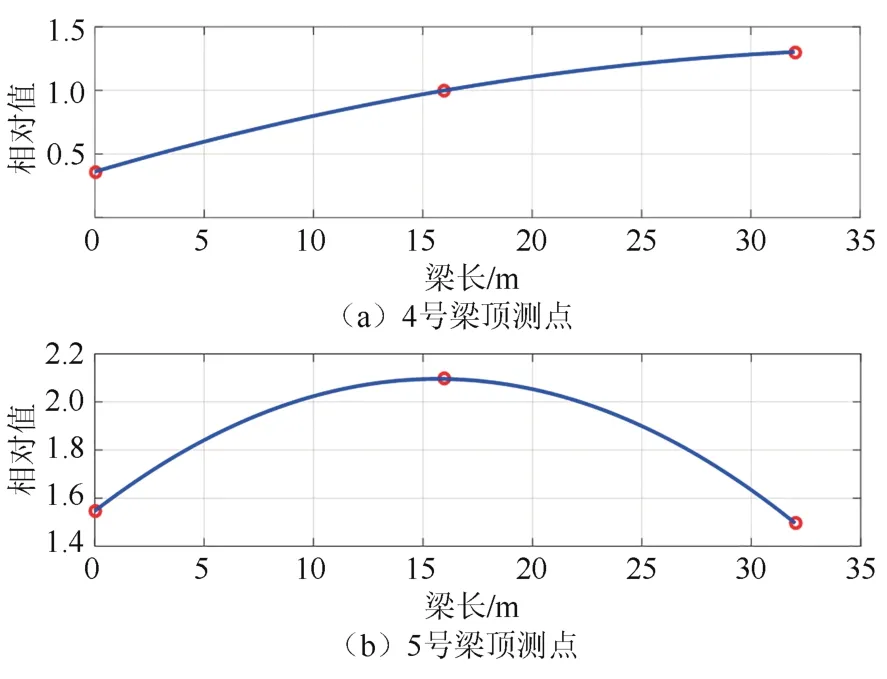
图10 4 号和5 号梁体振型图Fig.10 Mode shapes diagram of beams No.4 and No.5

以工况4 为例，对各测点进行自谱和互谱分析，以5 号梁顶测点l/2 处的振型幅值为参考点，做出与首峰频率2.25 Hz 对应的5 号梁、6 号梁振型如图11所示，可以看出5 号墩左右梁体的振型均为同侧振动，故也可利用首峰频率作为5 号墩桥墩参数识别的依据.

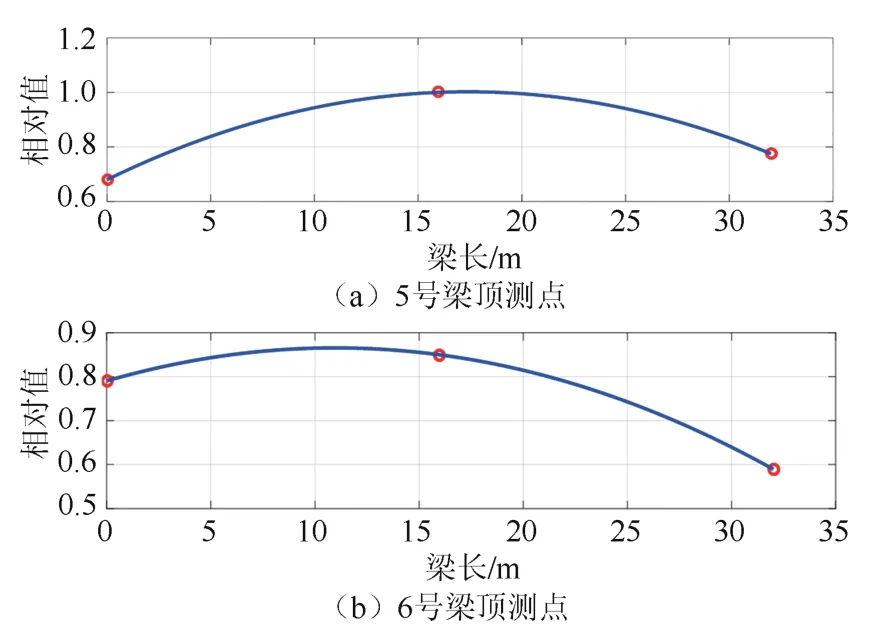
图11 5 号和6 号梁体振型图Fig.11 Mode shapes diagram of beams No.5 and No.6

3.2.4 数据对比

对比工况1（锤击激励）与工况2（环境激励）下梁体振型幅值数据如表4 所示，从表4 中可知两种工况下数值相差不大.同时可以看出工况3（锤击激励）与工况4（环境激励）的数据规律同工况1 与工况2 一致.基于所提梁体振型等效集中质量系数计算方法得到工况1 与工况2 下4 号墩顶等效集中质量系数α分别为1.04 和1.07，工 况3 与工况4 下5 号墩顶等效集中质量系数α分别为1.08 和1.13，说明提出的梁体振型等效集中质量系数的计算方法不受外部激励的影响.

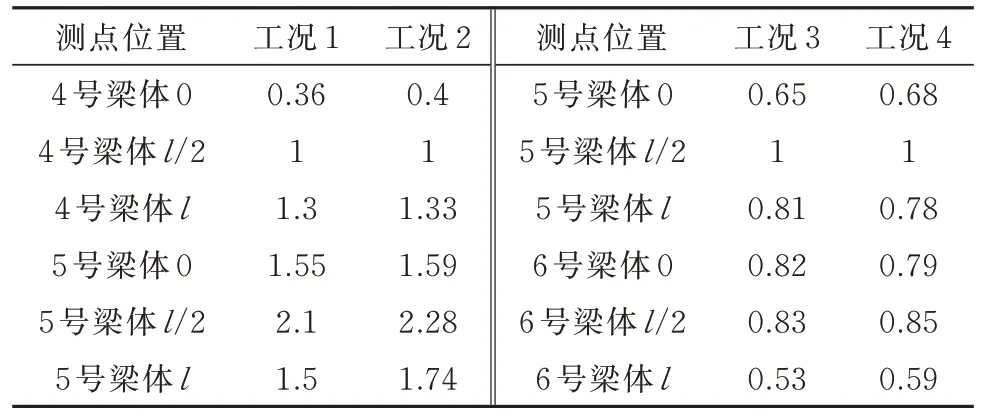
表4 振型幅值对比Tab.4 Comparison of mode shape amplitude

3.2.5 4 号、5 号水中桥墩参数识别

参考南排河特大桥工程概况，根据文献［16］利用m 法计算不同冲刷深度时，土体对桥墩的各方向约束值如表5 所示.采用Beam188 单元建立该桥墩有限元模型，且在墩身测点位置处建立相应的节点；采用弹簧单元Combin14 建立基础弹簧约束，采用Mass21 单元建立集中质量单元，根据墩顶振型等效集中质量的计算值，在墩顶以上梁高位置处附加上振型等效集中质量.桥墩截面、材料特性如表6 所示，有限元模型如图12 所示.

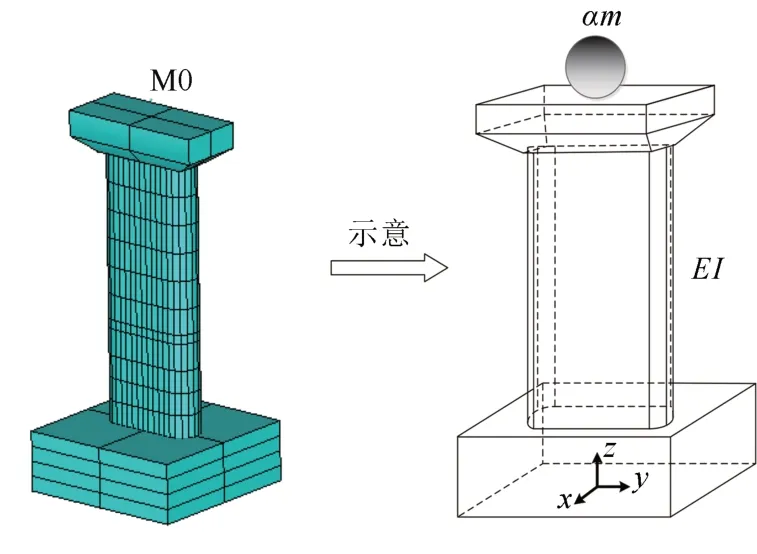
图12 桥墩有限元模型Fig.12 Finite element model of pier

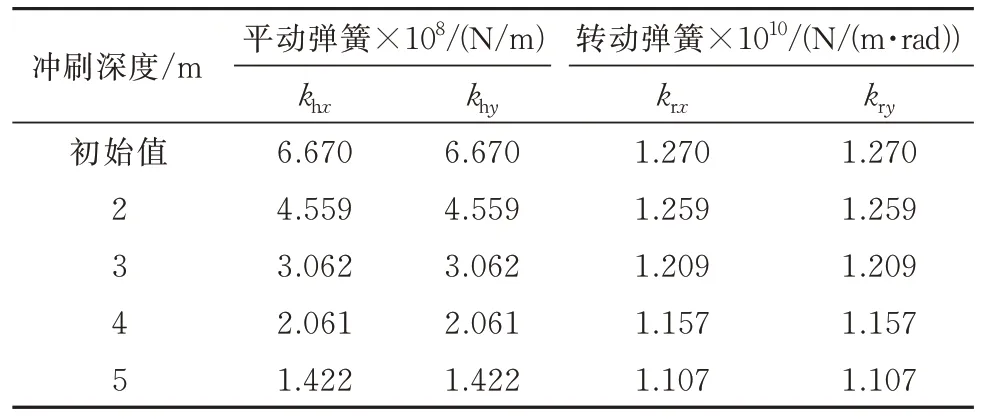
表5 基底弹性约束参数Tab.5 Elastic constraints of foundation bottom

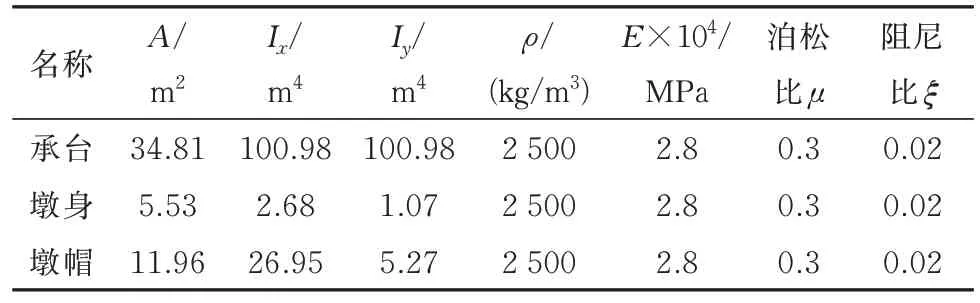
表6 有限元模型参数Tab.6 Parameters of finite element model

根据推导的等效集中质量系数计算方法，将工况一与工况二两次试验的墩顶集中质量系数取平均值α=1.055，将其作为4 号墩墩顶集中质量系数，将工况三与工况四求得的墩顶振型等效集中质量系数取平均值α=1.155，将其作为5 号墩墩顶集中质量系数.两个桥墩均利用首峰频率2.25 Hz 和与该频率对应的实测振型作为目标函数，将基底横桥向扭转弹簧刚度和横桥向水平弹簧刚度依据冲刷深度的关系作为一个待识别参数，墩身刚度EIx为另一个待识别参数，利用模型修正理论识别桥墩细部参数，识别出的参数及修正完成后的频率如表7 所示.4 号墩和5 号墩修正完成时的MAC1值均为0.999 8.

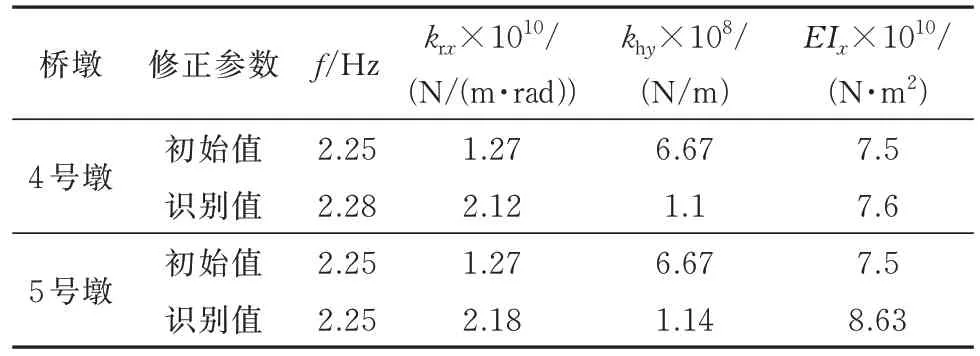
表7 4 号墩和5 号墩识别结果Tab.7 Identification results for piers No.4 and No.5

3.2.6 健康状态评估

采用提出的多跨简支梁桥桥墩健康状态定量评估准则对南排河特大桥4 号和5 号墩进行评估.

1）局部健康状态评估.

通过表7 中数据可以得出，4 号、5 号墩局部状态评估指标θp分别为1.01、1.15，均大于1，根据表1 局部健康状态评估准则，判定桥墩的局部健康状态为Ⅰ级，服役状态良好，满足设计要求.通过表7 中数据计算出，4 号、5 号墩冲刷病害的评估指标θf分别为1.67、1.72，均大于1，根据表2 冲刷病害评估建议准则，判定桥墩的局部健康状态为Ⅰ级，刚度高于设计值，健康状态良好.

2）整体健康状态评估.

根据初始状态下4 号、5 号墩的参数计算其横向线刚度为：899.7 kN/cm，根据识别值计算出4 号、5 号墩的横桥向线刚度值分别为：1 260.1 kN/cm、1 349.8 kN/cm，桥墩整体健康状态评估指标LSI 分别为1.4、1.5，均大于1，根据表3 整体健康状态评估准则，判定4 号、5 号墩桥墩的整体健康状态为Ⅰ级，服役状态良好，满足设计要求.

综合上述健康状态评估结果，可知4 号、5 号墩的整体的服役状态良好.

4 结论

1）基于弹性支撑梁振动理论以及能量守恒原理，推导了墩梁耦合体系振动过程中梁体等效集中质量的计算公式，进而提出多跨简支梁桥桥墩简化分析模型.基于简化模型，从桥梁构件性能和整体性能两方面提出一套完整的多跨简支梁桥桥墩健康状态快速评估方法及评估准则.

2）以南排河特大桥为试验对象，开展了桥墩健康状态评估试验.试验结果表明梁体振型等效集中质量系数计算方法不受外部激励的影响；提出的单墩简化分析模型可以较好地等效局部墩梁体系的振动；基于模态频率和振型构建的模型修正方法可以实现桥墩墩身刚度与基础约束的定量评估.

3）整体和局部健康评估结果均表明南排河特大桥4 号和5 号墩服役状态良好.该快速评估方法能够准确反映桥梁健康状态，从工程应用的角度验证了所提方法的实用性和可靠性.