扣件胶垫频变特性对车辆-轨道-桥梁耦合振动影响

崔巍涛，刘林芽，秦佳良

（华东交通大学铁路环境振动与噪声教育部工程研究中心，南昌 330013）

近年来高速铁路迅速发展，轨道交通高架桥梁因其占地面积小、高平顺性和高稳定性得到了广泛应用，已开通的京沪高铁与京津城际中桥梁比例达到了81%和77%，但随之产生的振动噪声问题也引起了人们的广泛关注［1-3］.扣件作为钢轨与下部结构的连接件，对维持钢轨和下部结构的可靠联结、缓解轮轨冲击、减小振动传播起着重要作用.扣件系统主要由弹性胶垫、扣压件等组成，其中扣件胶垫在扣件系统中主要提供弹性和阻尼，其属于橡胶高分子材料，具有黏弹性力学特性［4-5］，表现为动参数随环境温度和激振频率非线性变化.描述橡胶高分子材料动力特性最基本的模型是K-V（Kelvin-Voigt）和Maxwell 模型，其中K-V 模型也是目前车轨以及车桥耦合应用最多的扣件模型，这种模型简单直观，但是由于导数阶数为整数，不能反映加载历史的影响，难以准确描述橡胶材料的频变特性.为准确表征橡胶材料的力学特性，林松等［6-7］分别采用低阶分数导数模型来研究其力学性能，结果表明为较好吻合实验数据往往需要改进模型，增加了模型的复杂程度.赵永玲等［8］分别采用高阶分数导数模型和低阶分数导数模型表征橡胶材料的黏弹性，研究表明高阶FVMP（Fraction Voigt and Maxwell model in Parallel）模型能很好地描述橡胶材料的动态力学行为.

目前，一些学者结合扣件动参数频变对轮轨耦合振动特性展开了研究.杨麒陆等［9-10］研究了扣件阻尼频变对轮轨系统动力特性及地铁隧道环境振动的影响.Wei等［11-12］采用低阶分数阶Zener 模型表征扣件的频变特性来研究扣件动参数频变对轮轨垂向振动及衰减率的影响.Zhu等［13］采用分数阶K-V 模型表征扣件系统的幅频变特性来分析车轨耦合系统的动力响应.在以往的研究中，大多仅考虑扣件刚度频变或阻尼频变特性，使用的扣件模型在高频范围内表征扣件频变特性时也存在一定的误差，且扣件动参数频变对车桥耦合振动的影响研究较少.

鉴于此，为了准确描述扣件动参数与激振频率之间的关系，本文以高速铁路WJ-7 型扣件弹性胶垫为研究对象，通过试验测试并用FVMP 模型表征扣件的宽频动态特性，然后将其代入建立的车辆-轨道-桥梁耦合振动模型中，计算结构各部分的振动响应，并与采用传统K-V 模型的振动响应结果对比，探究扣件胶垫频变特性对车辆、轨道和桥梁振动的影响规律.

1 扣件胶垫频变特性研究

1.1 扣件胶垫FVMP 模型

FVMP 模型属于高阶分数导数模型，适用性广泛，能够在较宽的频率范围准确描述橡胶类材料的动态力学行为，FVMP 力学本构模型如图1 所示.

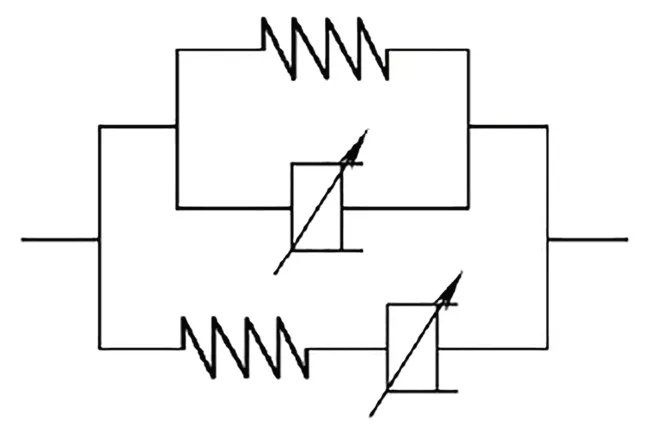
图1 FVMP 力学本构模型Fig.1 FVMP mechanical constitutive model

其时域本构方程为

1.2 FVMP 模型的参数识别

以高速铁路常用的WJ-7B 型扣件的弹性胶垫为研究对象，利用橡胶材料动态力学分析仪（Dynamic Thermomechanical Analysis）对弹性胶垫进行温度扫描试验，见图2.试验采用压缩模式，施加预荷载后，从-60℃扫描至40℃，激振频率为2 Hz，获取扣件胶垫动参数的温度谱.

图2 试验对象及设备Fig.2 Test object and equipment

在试验基础上，结合温频等效原理和WLF（Williams-Landel-Ferry）方程可转化得到扣件胶垫在常温（20℃）宽频下的储能、耗能模量和损耗因子，具体测试及转换方法参见文献［14］.最后，利用FVMP 模型来表征扣件胶垫的动力特性，结合式（2）～式（4），采用最小二乘法及遗传算法进行FVMP 模型的参数识别，拟合参数见表1.

表1 FVMP 模型拟合参数Tab.1 Fitting parameters of FVMP model

FVMP 模型与试验数据吻合良好，能够在宽频范围内准确描述扣件的动参数频变特性，如图3所示.

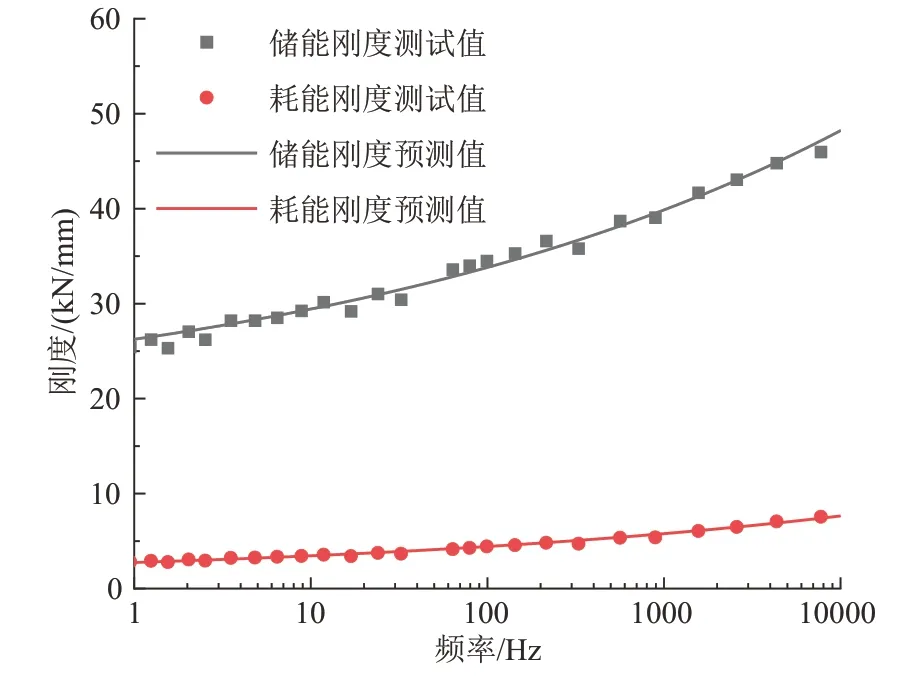
图3 预测值与试验值对比Fig.3 Comparison between predicted values and experimental values

在车辆-轨道-桥梁耦合时域分析模型中，常用刚度和阻尼来表示扣件的性质，故需将试验测得的储能刚度值和耗能刚度转化为常用的刚度和阻尼

式中：K为扣件的刚度；C为扣件的阻尼.

图4 为扣件胶垫转化后的刚度和阻尼值，说明扣件动参数与频率具有明显的相关性.但在目前车辆-轨道-桥梁耦合动力学计算时，大多采用3～5 Hz下的扣件刚度和阻尼值进行计算而未考虑动参数频变特性，这显然是不准确的，进而导致计算结果与实际产生一定的误差.

图4 弹性胶垫的刚度和阻尼值Fig.4 Stiffness and damping value of rail pads

2 车辆-轨道-桥梁耦合振动响应求解

图5 为建立的车-轨-桥耦合系统垂向模型，其中车辆和轨道采用Hertz 非线性弹性接触理论，钢轨与轨道板之间的联结由高阶分数导数FVMP 模型代替传统的K-V 模型，轨道板和桥梁通过连续的CA 砂浆层连接，底座板以参振质量的形式在桥梁模型中考虑.

图5 车辆-轨道-桥梁耦合系统垂向模型Fig.5 Vertical model of vehicle-track-bridge coupled system

2.1 车辆-轨道-桥梁耦合模型

2.1.1 车辆模型

车辆系统考虑车体的沉浮和点头运动，前后构架的沉浮和点头运动，以及4 个轮对的垂向振动共10 个自由度［15］.车辆系统振动微分方程为

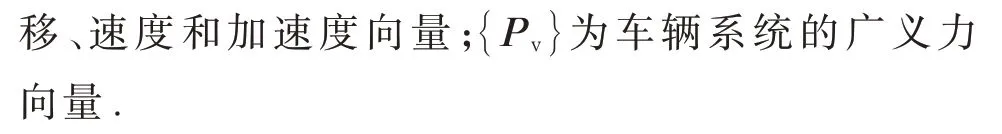
2.1.2 轨道模型

钢轨视为离散点支撑Euler 梁，采用Ritz 法求解，引入钢轨正则振型坐标qk(t)，得到钢轨振型坐标的二阶常微分方程组为

式中：Er、Ir分别为钢轨的弹性模量和截面惯性矩；mr、Lr为钢轨单位长度的质量和钢轨的总长度；Frsi(t)为第i个扣件位置处扣件支反力；Pj(t)为第j位轮轨作用力；xi和xwj分别为第i个扣件和第j个轮对沿线路纵向坐标；Zk(x)为钢轨的振型函数；nr为扣件的个数；Nr为钢轨的模态数.

轨道板视为有阻尼的弹性基础上的两端自由梁，忽略板与板之间的纵向连接，同样利用Ritz 法求解，引入轨道板正则振型坐标Tn，s(t)，得到轨道板振型坐标二阶常微分方程组为

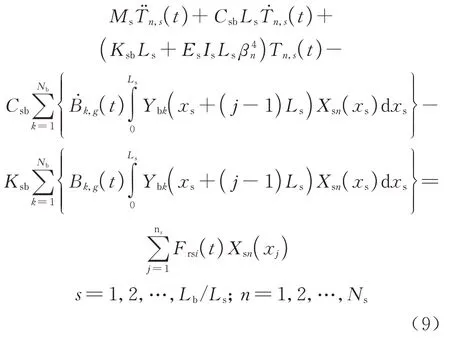
式中：Ms为轨道板的质量；Es、Is分别为轨道板的弹性模量和截面惯性矩；Ls为轨道板的长度；Ksb、Csb分别为轨道板下CA 砂浆层沿长度方向的分布刚度和分布阻尼；ns为一块轨道板上的扣件数；Ns为轨道板的模态数；Nb为桥梁的模态数；Bk，g()t为桥梁正则振型坐标；Xsn(xi)为轨道板的阵型正交函数；Ybk(xi)为桥梁的振型正交函数.

2.1.3 桥梁模型

桥梁同钢轨一样采用Euler 梁模型，利用Ritz 法求解，引入桥梁正则振型坐标Bk(t)，化简得桥梁振型坐标微分方程组的详细形式

式中：Eb、Ib分别为桥梁的弹性模量和截面惯性矩；mb为桥梁单位长度的质量；ζ为桥梁的各阶阻尼比；ωbn为单跨桥梁的第n阶圆频率；Lb为一跨桥梁的长度.

2.2 扣件FVMP 模型的应用

将式（1）采用Grünwald型微分求解，分别对Dα Frs(t)、Dα X(t)、Dβ X(t)、Dγ X(t)、Dα+γ X(t)按照分数导数定义展开得

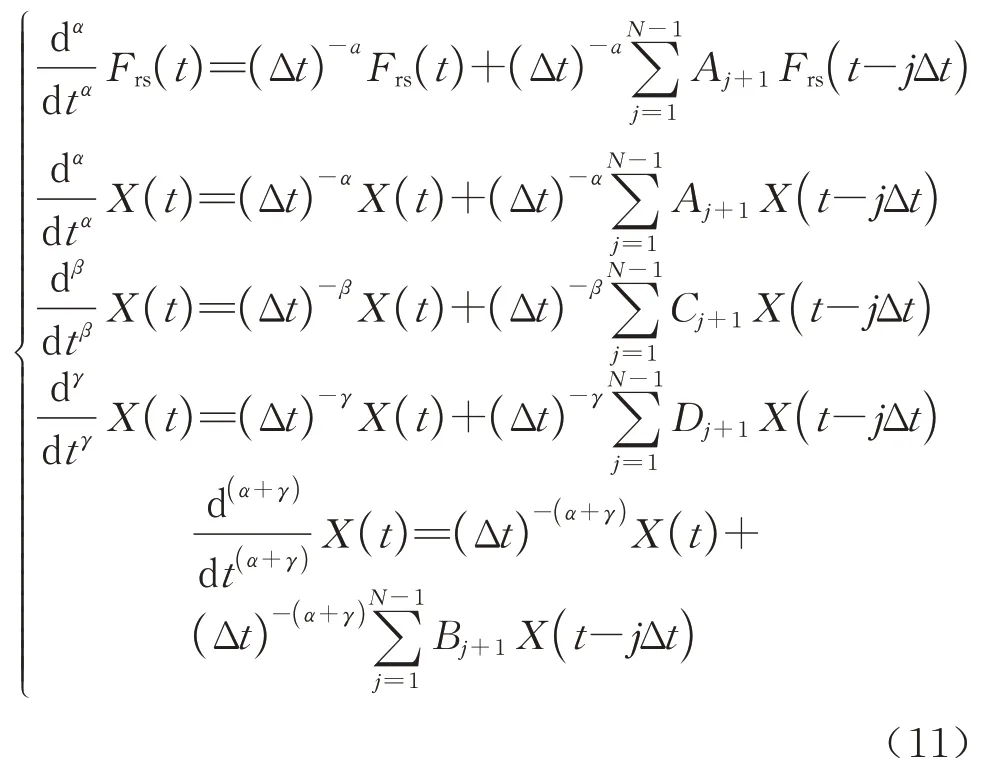
式中：Δt为数值积分步长；N为积分步数，一般取160可得到满意的结果；Aj+1、Bj+1、Cj+1、Dj+1分别为不同分数阶导数对应的Grünwald 系数.

将式（11）代入到式（1）中，进行化简即可得到高阶分数阶导数FVMP 模型所对应的扣件力表达式为

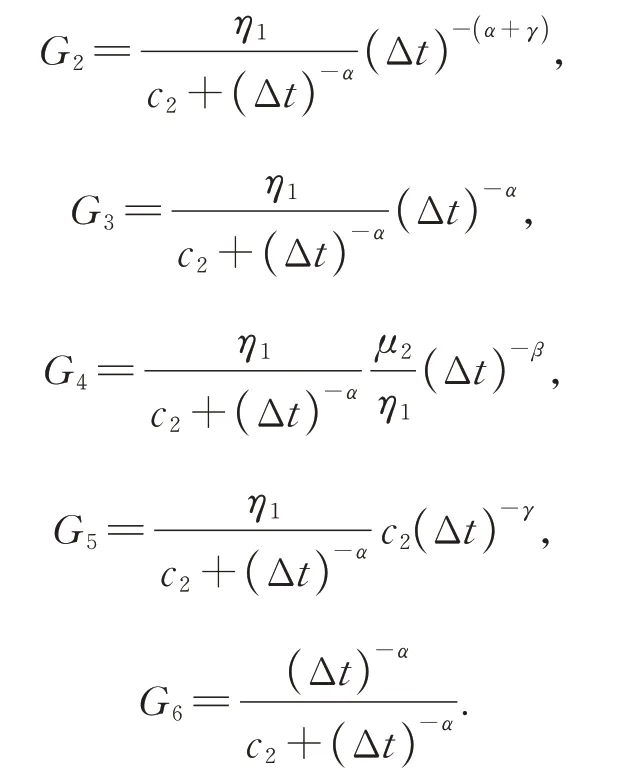
将式（12）分别代入式（8）和式（9），便得到考虑扣件动参数频变特性的钢轨和轨道板的振动微分方程组的具体形式.

2.3 数值积分方法

将式（7）～式（10）联立得到最终的车-轨-桥耦合动力学微分方程组，采用新型显式积分法求解.其积分格式为

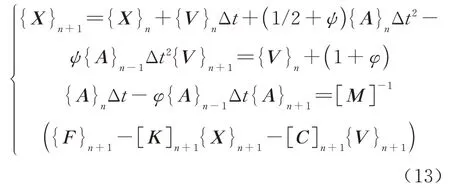
式中：ψ和φ为积分常数，取ψ=φ=0.5；Δt取0.1ms；下标n-1、n和n+1分别代表第n-1、n和n+1 时刻.初始条件设为{X}0={V}0={A}0={0}.

2.4 计算参数

车辆参数见表2，轨道和桥梁结构的具体参数见表3.

表2 CRH380 高速客车的动力学参数Tab.2 Dynamic parameters of CRH380 high-speed train

表3 轨道和桥梁参数Tab.3 Track and bridge parameters

本文以中国高速铁路无砟轨道的高低不平顺谱作为激励源［15］，波长为0.5～200 m，采用傅里叶逆变换法［16］获取不平顺的时域样本作为输入，见图6.

图6 中国高速铁路无砟轨道高低不平顺谱Fig.6 Power spectrum density of ballastless track irregularities for Chinese high-speed railway

3 扣件胶垫频变对车-轨-桥振动影响

为了研究扣件胶垫频变特性对车-轨-桥振动响应的影响，设计了两种工况，工况一为采用K-V 模型，取值参考相关规范［17］，取温度20℃、激振频率为4 Hz下的刚度和阻尼，根据图4，刚度为28.038 kN/mm，阻尼为0.135 kN·s/mm；工况二为采用考虑了频变特性的FVMP 模型，按表1 取值.列车运行速度为350 km/h，计算车辆通过九跨简支梁的计算结果，对比分析车辆、轨道和桥梁结构的动力响应，并采用1/3 倍频程方法分频段对比分析扣件频变动参数和常量动参数计算得到的振动响应.

3.1 对车辆的影响

图7 为两种工况下车体振动加速度的时频域对比图.由图7（a）可知，两种情况下的车体加速度均在-0.2～0.2 m/s2范围内变化且差别较小，远小于机车运行平稳性限值2.5 m/s2.由图7（b）可知，两条曲线基本重合，第一主频在1 Hz 附近，这与车体的自振有关.扣件的频变特性对车体振动影响很小，这是因为一系和二系悬挂削弱了扣件频变特性对车体的影响.

图7 车体振动加速度对比Fig.7 Comparison of vibration acceleration of vehicle

3.2 对轮轨力和扣件力的影响

图8 为两种情况下第五跨桥梁跨中扣件力的时频域对比图.由图8（a）可知，考虑扣件频变特性时，扣件力最大值为22.989 kN，不考虑扣件频变特性时，扣件力最大值为21.936 kN，峰值增大4.80%.由图8（b）可知，考虑扣件频变特性，扣件力在20 Hz 以下基本无变化，在40～80 Hz 范围内有所增大，在20～31.5 Hz 和100～250 Hz 范围内减小.

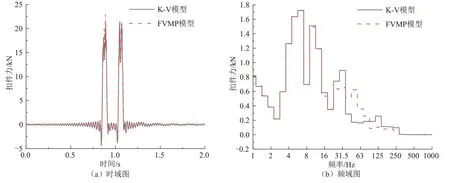
图8 扣件力对比Fig.8 Comparison of rail pad force

图9 为两种工况下轮轨力的时频域对比图.由图9（a）可知，考虑扣件动参数频变时，轮轨力幅值增大，最大值为92.764 kN，不考虑动参数频变时，轮轨力的最大值为84.689 kN，峰值相差9.53%.由图9（b）可知，轮轨力在25 Hz 以下结果基本一致，在25～80 Hz 和800 Hz 以上范围频变动参数的计算结果大于常量动参数的计算结果，其中在中心频率50 Hz 处增大了1.699 kN，轮轨耦合共振频率在该频段，说明考虑扣件动参数频变会放大轮轨耦合共振的影响；在80～250 Hz 范围内频变动参数的计算结果小于常量动参数的计算结果.

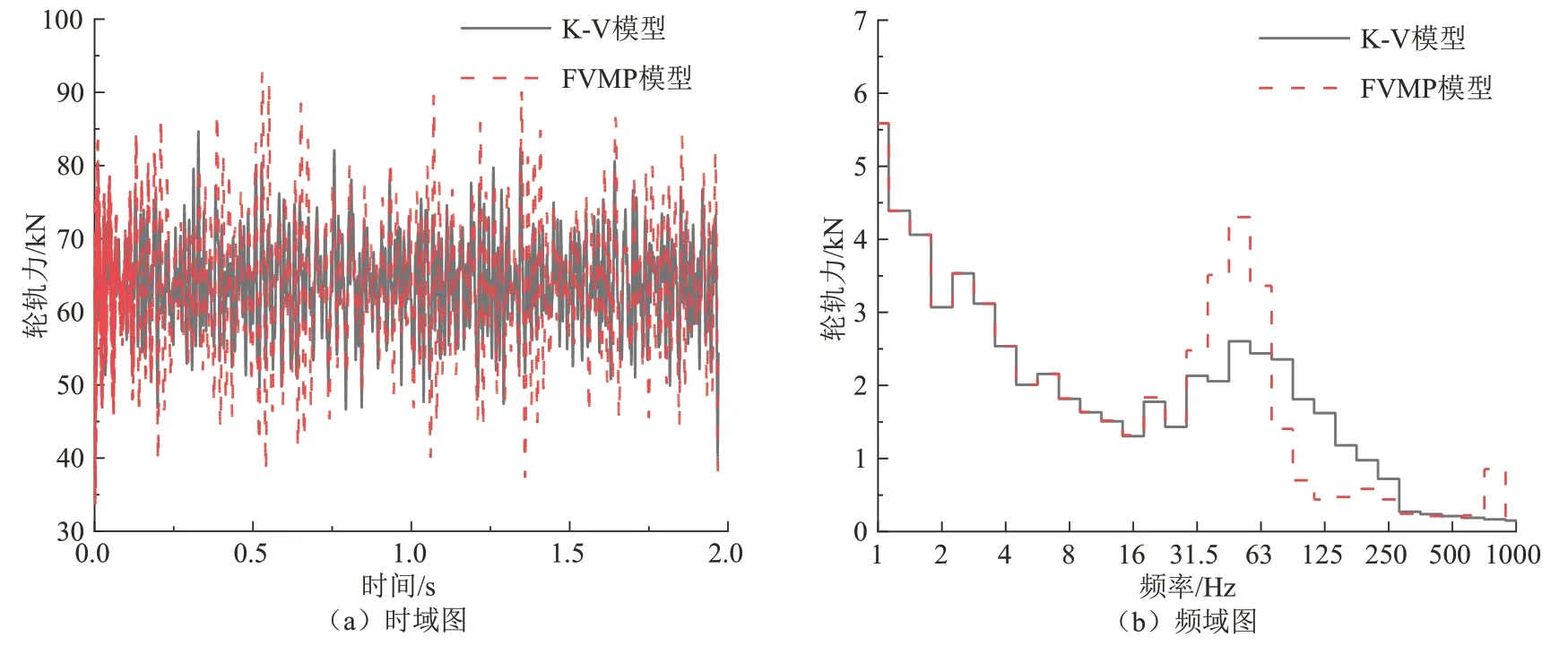
图9 轮轨力对比Fig.9 Comparison of wheel-rail force

3.3 对钢轨的影响

图10 为两种工况下的跨中钢轨相对桥面板的位移时程图.由图10 可知，扣件动参数取常量时，钢轨位移最大值为0.780 mm，当考虑扣件动参数频变时，钢轨位移最大值为0.927 mm，增幅17.7%.说明考虑扣件频变特性会导致钢轨位移有所增大.

图10 钢轨位移对比Fig.10 Comparison of rail displacement

图11 为两种工况下的跨中钢轨的加速度时频域图.由图11（a）可知，考虑扣件动参数钢轨加速度明显增大，钢轨加速度最大值为43.741 m/s2，不考虑扣件频变特性，钢轨加速度最大值为29.521 6 m/s2，增幅48.17%.由图11（b）可知，考虑扣件频变动参数，钢轨加速度在16 Hz 以上基本无变化，在中心频率31.5 Hz 处有所减小，在63 Hz 以上明显增大.

图11 钢轨加速度对比Fig.11 Comparison of rail acceleration

3.4 对轨道板的影响

图12 为两种工况下第五跨桥梁跨中轨道板相对桥面板的位移时程图.由图12 可知，考虑扣件动参数频变，轨道板位移有所增大，轨道板位移最大值为0.077 mm，不考虑扣件动参数频变，轨道板位移最大值为0.068 mm.

图12 轨道板位移对比Fig.12 Comparison of track slab displacement

图13 为两种工况下轨道板加速度时频域图.由图13（a）可知，考虑扣件动参数频变时，轨道板加速度幅值减小但波动变大，轨道板加速度最大值为11.826 m/s2，不考虑扣件频变特性轨道板加速度最大值为7.972 m/s2.由图13（b）可知，考虑扣件频变特性，轨道板加速度在31.5 Hz 以下变化较小，在40～80Hz明显增大，在100～500Hz减小，在500Hz以上则增大.

图13 轨道板加速度对比Fig.13 Comparison of track slab acceleration

3.5 对桥梁的影响

图14 为两种工况下的第五跨桥梁的跨中位移图.由图14 可知，桥梁位移曲线图吻合较好，说明扣件动参数频变对桥梁垂向位移几乎没有影响.

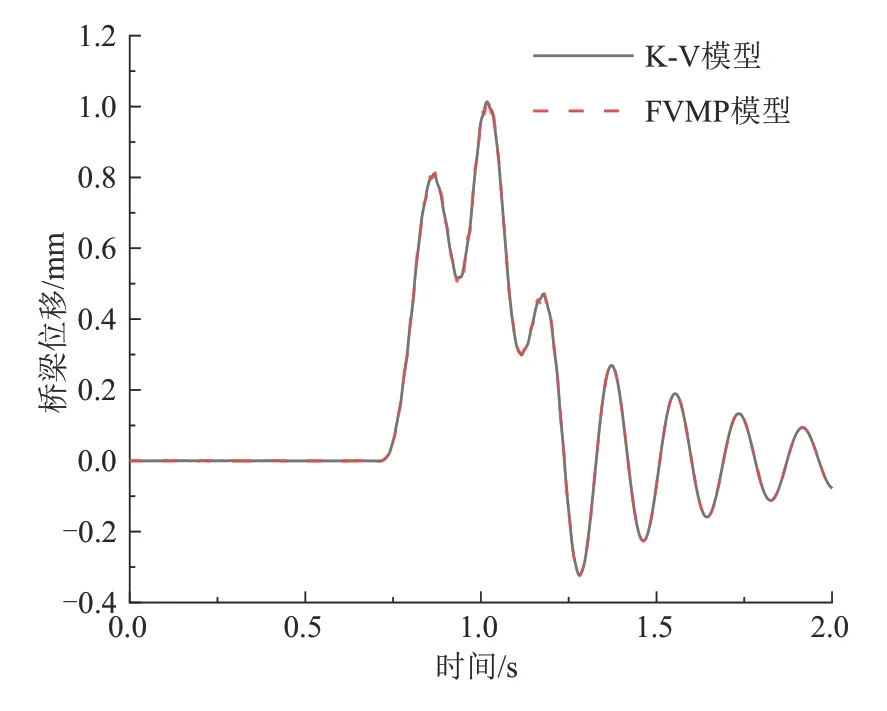
图14 桥梁跨中位移对比Fig.14 Comparison of bridge mid-span displacement

图15 为两种工况下桥梁加速度时频域对比图.由图15（a）可知，考虑扣件动参数频变时，桥梁加速度有所变大，最大值为1.588 m/s2，不考虑扣件频变特性桥梁加速度最大值为0.983 m/s2.由图15（b）可知，考虑扣件频变特性，桥梁加速度在40 Hz 以下变化较小，在40～80 Hz 明显增大，在100～250 Hz 减小.在63 Hz 附近出现明显峰值，与轮轨耦合系统的共振有关.

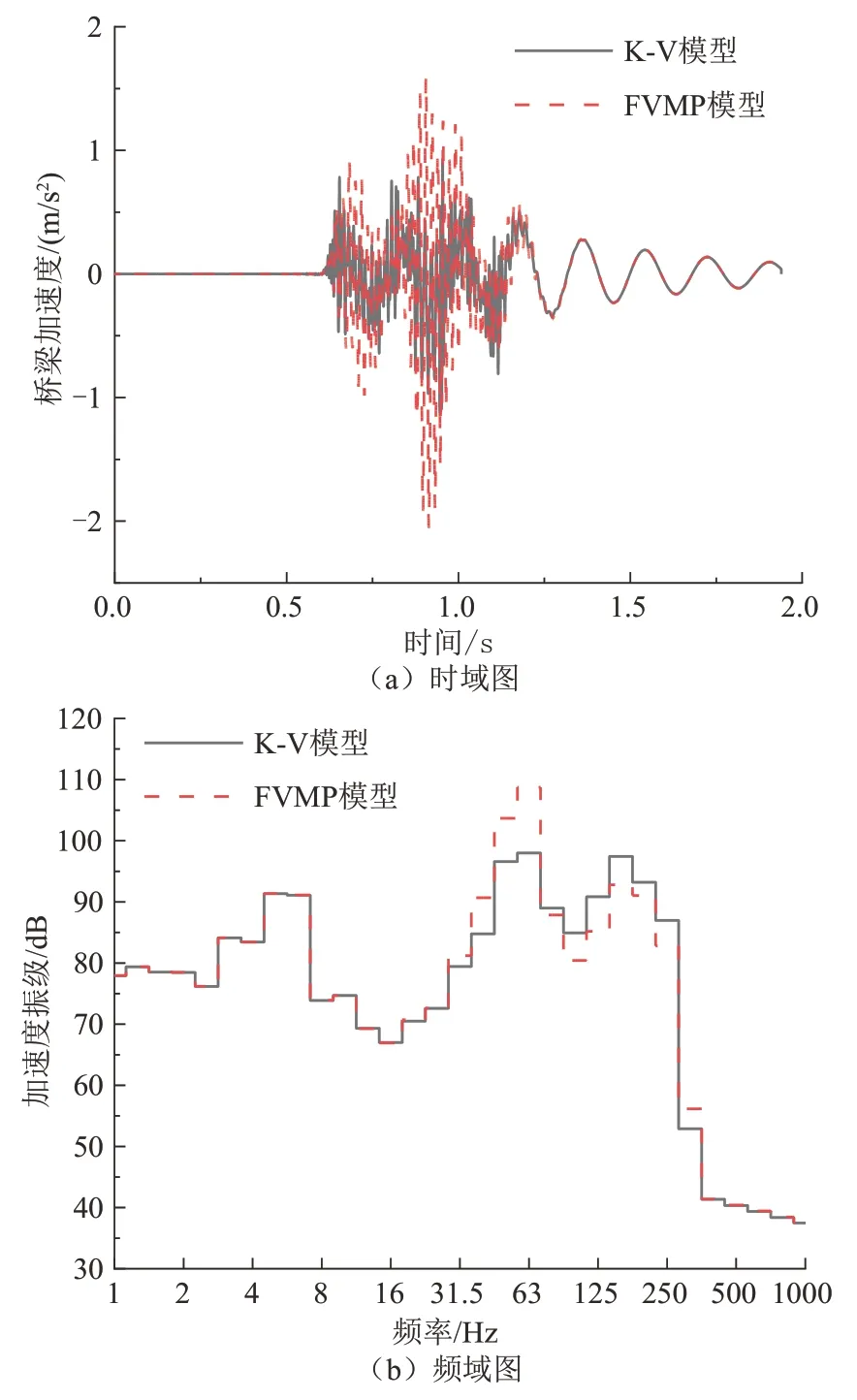
图15 桥梁加速度对比Fig.15 Comparison of bridge acceleration

4 结论

1）扣件的动参数与激振频率呈现非线性变化，具有明显依赖性.其刚度随着频率的升高而增大，阻尼随着频率的升高而减小，采用FVMP 模型能在宽频范围内准确描述扣件的动参数频变特性.

2）考虑扣件频变特性时，从时域响应来看，轮轨力和扣件力明显增大，峰值分别增大9.53% 和4.80%.从频域响应来看，轮轨力和扣件力在低频基本无变化，在40～80 Hz 明显增大，在80～250 Hz 减小.其中轮轨力在63 Hz 附近出现峰值，这是因为车轨耦合系统的固有频率处于该范围，考虑扣件频变特性会揭示中高频段轮轨耦合系统共振的事实.

3）考虑扣件动参数频变特性，从时域响应来看，车体垂向振动加速度和桥梁位移几乎无变化，钢轨加速度、桥梁加速度明显增大，在各峰值分别相差48.17%和38.10%.从频域响应对比来看，扣件胶垫的频变特性对结构振动响应的影响主要存在于中高频段内，钢轨在整个中高频振动明显加剧，轨道板和桥梁在车轨耦合系统的固有频率处振动明显增大.

4）在实际工程中对轨道、桥梁结构振动响应进行预测分析时，应考虑扣件胶垫的频变特性来提高预测的精度.