内部激励下高速动车齿轮箱振动响应评估

胡玉飞，张建超，陈湛，王军

（石家庄铁道大学a.机械工程学院，b.省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043）

高速动车齿轮箱传动系统主要由一对大小斜齿轮啮合组、箱体、滚动轴承以及联轴节组成.其中箱体由上箱体与下箱体两部分构成，通过螺栓将上下箱体固定连接为一体，大齿轮箱体部分通过轴承与车轴相连接，小齿轮箱体部分采用C 型支架将其与构架相连接［1-2］.齿轮箱滚动轴承类型包含有球轴承、圆柱滚子轴承以及圆锥滚子轴承3 种类型［3-4］.

在齿轮箱传动系统的数学模型研究方面，任朝晖等［5］采用集中质量法建立了多自由度斜齿轮-转子-轴承弯扭轴耦合的动力学模型.分析了转速、齿轮偏心、轴承游隙等参数对传动系统振动响应特性的影响.研究结果表明：传动系统中扭转振动位移明显大于横向和轴向振动位移，系统以扭转振动为主.张孔亮等［6］建立了箱体-轴承-齿轮耦合动力学模型，计算获取了齿轮副动态啮合力、齿轮箱体表面的振动加速度和位移.发现了齿轮箱箱体动态响应能量主要集中在齿轮啮合频率及其倍频处，并通过实验验证了仿真结果的准确性.

在齿轮箱传动系统的三维仿真模型研究方面，Wang等［7］通过多体动力学仿真软件建立了含有传动系统的高速动车车辆-轨道耦合仿真模型，分析了齿轮箱在轨道不平顺激励下的应力分布特性，结果表明箱体油位观察孔与底面的应力水平明显增加.Ren等［8］基于某型动车组参数，建立了含有传动系统的铁路车辆刚柔耦合动力学模型，研究了车辆在不同运行工况下的齿轮接触特性和齿轮箱振动特性对车体的影响，结果表明，齿轮箱振动对车体的振动几乎无影响.孙刚等［9］通过多体动力学软件建立了包含齿轮传动系统振动的动车组刚柔耦合系统动力学模型，研究了多种工况下传动系统的动力学性能与车辆系统主要部件间的相互作用，得到了传动系统振动对构架和齿轮箱振动有一定影响.黄冠华等［10］针对高速列车齿轮箱箱体结构的动态响应问题，建立了高速列车的整车仿真模型，其内部激励主要考虑齿轮的时变啮合刚度、轮齿啮合阻尼以及传递误差，外部激励主要考虑轨道不平顺激励，结合箱体自身的模态频率，发现了齿轮箱箱体振动特性主要受齿轮啮合的高频振动影响较大.杨柳等［11］建立了机车传动系统有限元单元的动态模型，分析了齿轮啮合刚度、轴承支撑刚度、轮轨接触力作用下传动系统齿轮单元的幅频响应变化，结果表明，复杂环境因素下，传动系统齿轮啮合频率及固有频率处，系统振动响应较大.

通过上述研究中可知，不论是传动系统的数值模型还是三维仿真模型，相对于考虑齿轮啮合接触的文献较多，而对于同时考虑齿轮啮合接触和轴承内部接触的传动系统三维仿真模型的研究较少.因此，本文从仿真角度对齿轮箱传动系统进行研究，同时考虑齿轮啮合接触和轴承内部接触，并通过理论计算确定齿轮箱传动系统的仿真参数，对齿轮啮合接触特性、轴承滚动接触特性以及箱体振动特性与各部件间的振动特性的影响进行研究.

1 齿轮箱刚柔耦合动力学模型

齿轮箱传动体系统分别由箱体（1 个）、小齿轮（1 个）、大齿轮（1 个）以及滚动轴承（5 套）组成.绘制齿轮箱传动系统动力学模型的拓扑图，如图1 所示.其中滚动轴承中有2 套为无内圈的圆柱滚动轴承分别安装与小齿轮轴两侧（轴承1 与轴承2），从而小齿轮轴与圆柱滚动体直接接触；对于轴承3、轴承4 及轴承5 则通过其内圈分别与小齿轮轴、大齿轮轴相固定约束，同时并对大、小齿轮间和滚动轴承内部施加接触，从而构成齿轮箱传动系统动力学模型.

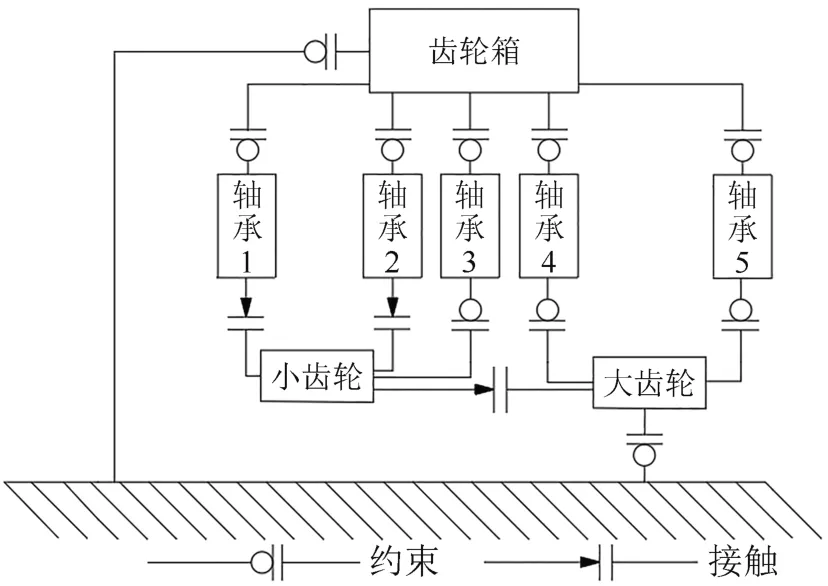
图1 齿轮箱传动系统动力学模型拓扑图Fig.1 Topological diagram of the dynamic model of the gearbox transmission system

滚动轴承内部的接触形式为滚动体与内圈接触、滚动体与外圈接触以及滚动体与保持架接触3 种.在Adams 中的滚动轴承接触和齿轮啮合接触中采用碰撞模型，其中Adams 将两个存在接触形态的刚体模型等效为弹簧阻尼模型，如图2 所示.

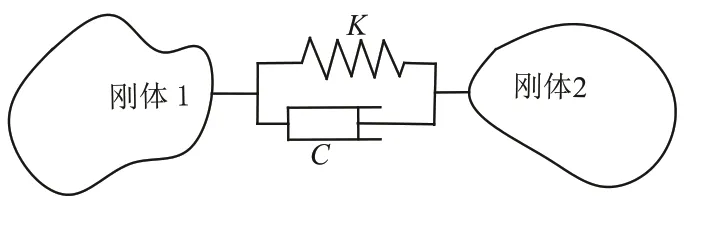
图2 接触碰撞模型Fig.2 Contact-collision model

将两物体间的接触力通过弹性力和阻尼力的数学形式来表达，其表达式为

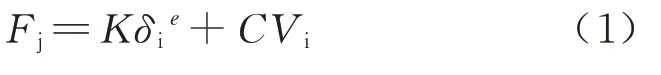
式中：Fj为法向接触力，N；δi为接触点处的法相穿透深度，一般取值选择0.1，mm；e为力指数，对于刚度较大的e＞1，否则e＜1.对于金属e常用取值为1.3～1.5；C为阻尼系数，一般取刚度值的0.1%～1%，N·sec/mm；Vi为接触点的法向相对速度，mm/sec；K为Hertz接触刚度，N/mm.

刚度系数K取决于相互碰撞物体的材料与结构形式，计算公式为

式中：R为综合曲率半径；E为综合弹性模量.具体计算公式为

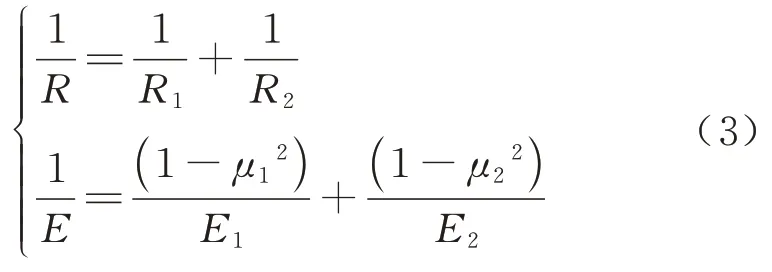
式中：E1、E2分别为两个接触物体材料的弹性模量；μ1、μ2分别为两个接 触物体材料的泊松比；R1、R2分别为两接触物体接触点的当量半径.

齿轮箱箱体的柔性文件则通过有限元软件对箱体进行网格划分、添加约束、添加刚域等.其中仿真过程中的难点为：滚动轴承需以子装配体形式存在于总装配体中，否则无法在仿真过程中实现内圈转动、外圈固定以及滚动体公转；滚动轴承滚动体公转速度主要受滚动体与内圈间干涉量、静摩擦系数以及动摩擦系数影响；斜齿轮啮合力大小主要受两齿轮间的接触刚度、静摩擦系数以及动摩擦系数影响.其中齿轮箱传动系统的刚柔耦合模型如图3所示.

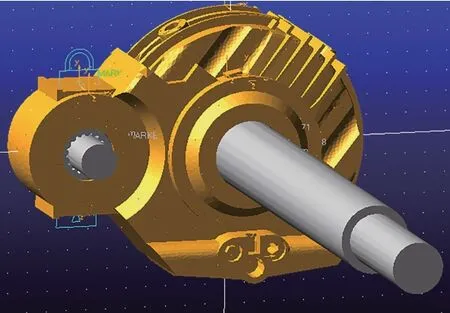
图3 齿轮箱传动系统的刚柔耦合模型Fig.3 Rigid-flexible coupling model of gearbox transmission system

2 高速动车斜齿轮受力分析

斜齿轮在啮合过程中，轮齿所受总法向力Fn位于同轮齿相垂的法面上，可将其分解为径向力Fr、轴向力Fa、圆周力Ft，其中斜齿啮合受力分析图如图4所示.

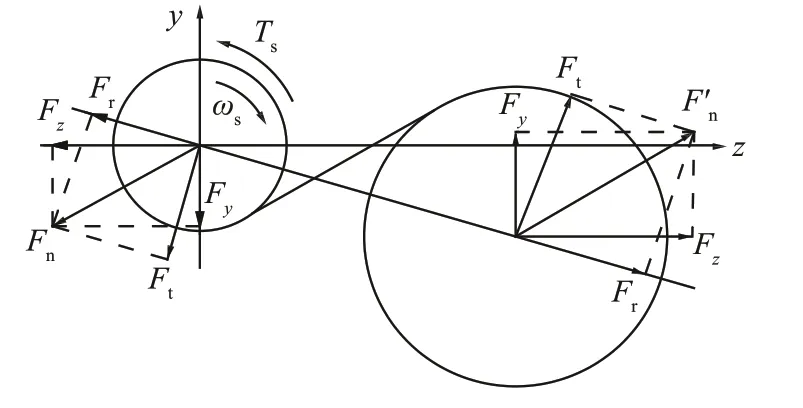
图4 斜齿啮合受力分析Fig.4 Force analysis of helical gear meshing

图4中Ts为主动轮所受转矩；ωs为主动轮角速度；F'n为斜齿轮在啮合过程中所受的总法向力在旋转平面内的投影，即F'n=Fncosα，α为总法向力与水平面夹角，β为总法向力的初始相位角.主动轮所受轮齿接触力沿y，z方向的接触力为

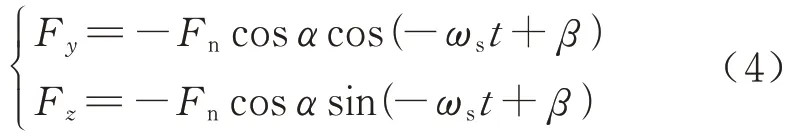
小齿轮处所受啮合力大小为

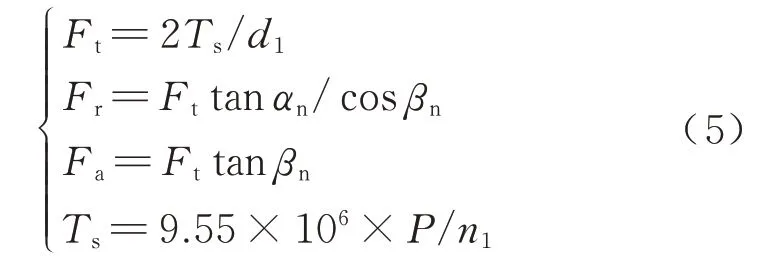
式中：αn为斜齿轮法面压力角，deg；βn为斜齿轮螺旋角，deg；P为电机持续输入功率，kW；n1为小齿轮转速，r/min；d1为小齿轮分度圆直径，mm.其中齿轮啮合模型如图5 所示.

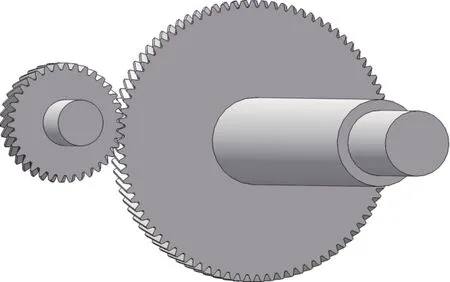
图5 斜齿啮合仿真模型Fig.5 Simulation model of helical gear meshing

3 滚动轴承模型

3.1 轴承滚动体与外圈的接触力计算

由赫兹接触理论［12-13］可知，滚动体与滚道的接触负荷均匀分布，以圆锥滚子轴承为例，圆锥滚子轴承在动载过程中的离心力作用下，滚子受力图如图6 所示.

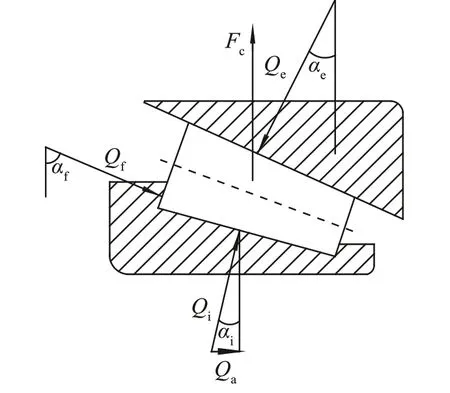
图6 圆锥滚子轴承动载时受力Fig.6 Forces model of tapered roller bearings under static loading

圆锥滚子轴承运转过程中圆锥滚子受到与内滚道、外滚道、大挡边3 个接触力以及滚动体离心力作用.其中，Qi为滚子与内滚道间的法向接触力，Qf为滚子与大挡边间的法向接触力，Qe为滚子与内滚道间的法向接触力，Fc为滚动体离心力，αe、αf、αi分别为接触力与垂向平面夹角，Qa为滚子与内滚道间的法向接触力的轴向分力.由滚子的平衡方程可求出外滚道的接触力为

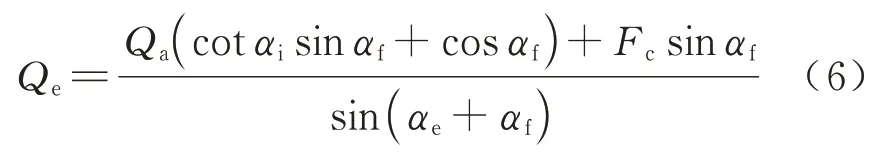
其中，离心力不影响Qa大小，其大小可由滚子静负荷分析中计算得出.

对于球滚动体离心力与圆柱（锥）滚动体离心力计算方法分别为

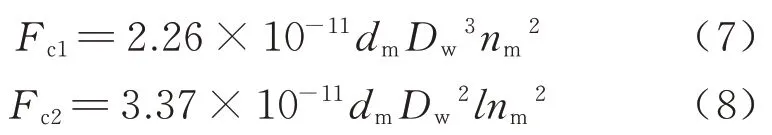
式中：dm为滚子组中心距，mm；Dw为滚动体直径，对于圆锥滚子为平均直径，mm；l为滚子长度，mm；nm为滚动体公转速度，r/min.

根据滚动体无滑动条件，滚动体在接触点（线）钢球（滚子）与内外滚道线速度相同.滚动体公转速度为

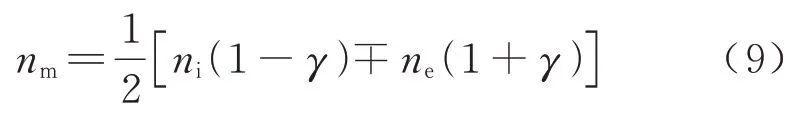
式中：ni为内圈转速，r/min；ne为外圈转速，r/min；γ为无量纲几何参数，其中γ=Dwcosαj/dm；αj为接触角，deg.当内圈转向与外圈转向相反时取负号；当内圈转向与外圈转向相同时取正号.

3.2 轴承座受力分析

对于轴承座的受力分析，建立了小齿轮与大齿轮处的参考坐标系如图7 所示.其中O1为小齿轮中心位置，O2为大齿轮中心位置，1 号、2 号、3 号、4 号、5 号分别为5 个滚动轴承的位置标记.h1、h2、h3、h4、h5分别为小、大齿轮中心与5 个滚动轴承中心距离长度，其大小数值依次为h1=65 mm、h2=79 mm、h3=62 mm、h4=100 mm、h5=100 mm.

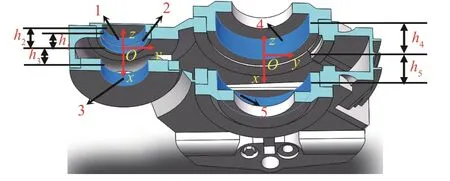
图7 小、大齿轮参考坐标系Fig.7 Small and large gear reference coordinate system

对小齿轮轴进行受力分析，其中1 号轴承处只受轴向力作用；2、3 号轴承处不承受轴向力作用，对于轴承各x、y、z方向受力计算为

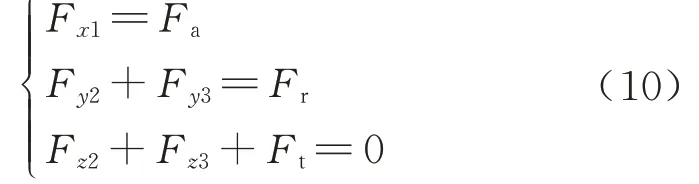
对于轴承各Mx、My、Mz方向受力计算为

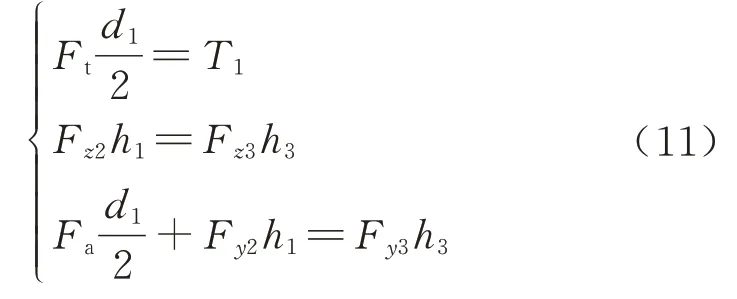
联立式（5）～式（11）可求得1 号、2 号、3 号轴承座处受力Fxi、Fyi、Fzi（i=1、2、3）.

对于大齿轮轴处受力分析时以O2-xyz为参考坐标系，采用式（10）～式（11）方法可求得4 号、5 号轴承座处受力情形.其中对于各滚动轴承仿真模型如图8 所示.

图8 各滚动轴承仿真模型图Fig.8 Simulation model diagram of rolling bearings

4 齿轮箱传动系统动力学仿真

齿轮箱传动系统仿真工况设定时长1 s，小齿轮加速时长0.1 s，匀速时转速为4 200 r/min，当仿真单位为deg/s 时，对应转速为25 200 deg/s.其中小齿轮端旋转驱动函数为：STEP=（time，0，0，0.1，-25 200 d）.同时，为防止负载转矩突变而影响箱体的振动响应，在大齿轮轴处通过STEP 函数添加负载转矩，大小为3 000 000 N·mm，即：STEP=（time，0，0，0.1，-3 000 000）.

4.1 齿轮啮合仿真结果

根据斜齿轮啮合关系，大、小齿轮啮合力与转速仿真结果如图9 所示，其中0～0.1 s 时间内，两齿轮间处于加速状态；在0.1～1.0 s时间内为齿轮匀速状态，该时间段内齿轮啮合力的3 个方向分力均表现出规律性较强的波动.根据图9（b）可知，小齿轮转速为4 200 r/min，大齿轮转速为1 730 r/min.

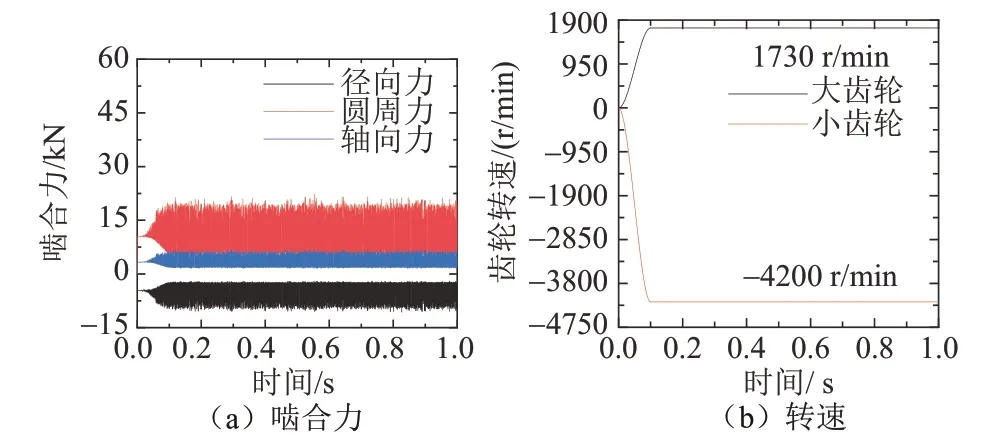
图9 齿轮啮合力与转速结果Fig.9 Force and speed results during gear meshing

齿轮啮合力频谱图，如图10 所示.由图10 可知，齿轮啮合过程中主要转频成分有主动轴转频H1（n1/60=70 Hz）和啮合频率Hm（n1×z1/60=2 450 Hz），相对于从动齿轮转频H2（n2/60=28.8 Hz）表现不明显.由此可知，齿轮啮合传动在运行过程中的频域中，主频信息主要包含齿轮转频与齿轮啮合频率.

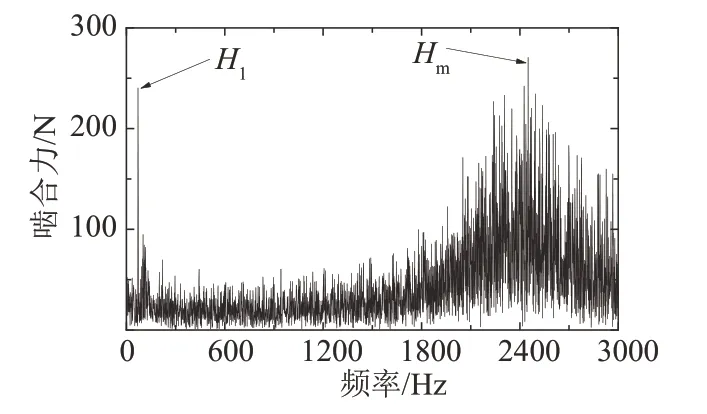
图10 齿轮啮合力频谱图Fig.10 Spectrum diagram of gear meshing force

对于大、小齿轮的振动加速度如图11 所示.由图11 可知，小齿轮处振动加速度明显高于大齿轮处振动加速度，由此可知，两齿轮在啮合过程中对小齿轮处的振动特性影响较大.

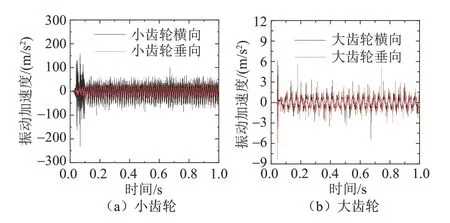
图11 大、小齿轮振动加速度Fig.11 Vibration acceleration of large and small gears

大、小齿轮质心位置位移轨迹如图12 所示.由图12 可知，大、小齿轮质心位移在yz平面的运动轨迹较为规则基本为圆形，说明大、小齿轮稳定性较好，其中小齿轮质心位移范围为-0.09 mm～0.09 mm，大齿轮质心位移范围为-0.2×10-7mm～0.2×10-7mm，相较于二者质心位移范围差别较大，其原因在于小齿轮处振动情形大于大齿轮处振动情形.

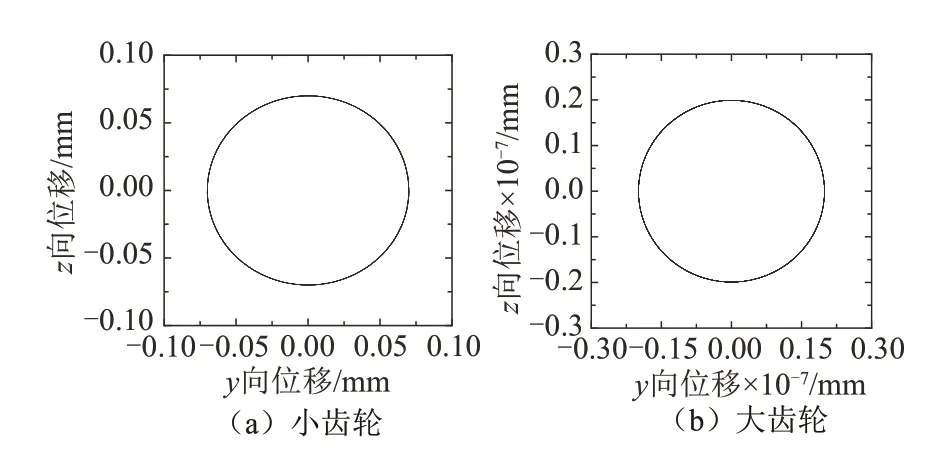
图12 大、小齿轮质心在yz 平面位移轨迹Fig.12 Displacement trajectory for center of mass in large and small gears in yz plane

根据对齿轮啮合的圆周力、径向力、轴向力以及转速的计算值与仿真值对比结果，仿真结果值略大于计算结果值，分析其原因为齿轮在啮合过程中存在冲击、碰撞等因素，而理论计算过程为较为理想的运行环境，从而使得齿轮啮合力的实际结果大于计算结果.其中对比结果见表1 所示.

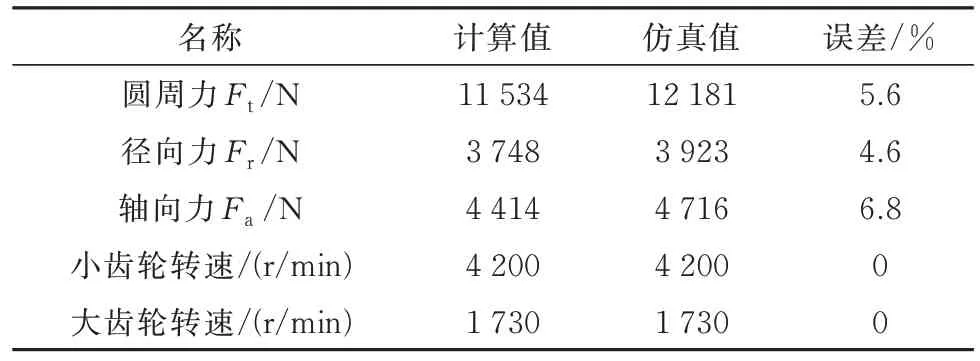
表1 齿轮啮合仿真结果对比Tab.1 Comparison of simulation results during gear meshing

综上所述，通过齿轮啮合处的仿真结果与计算结果对比，可以得出齿轮啮合力部分的仿真结果能够反映实际工况下的斜齿轮啮合作用，并且在斜齿轮啮合频域中包含有小齿轮转频和齿轮啮合的啮合频信息.通过大、小齿轮处的振动加速度结果与大、小齿轮质心处的位移结果对比，发现了小齿轮处的振动响应与小齿轮质心处位移分别高于大齿轮处结果值，由此可知，大齿轮的稳定性要优于小齿轮.

4.2 滚动轴承仿真结果

齿轮箱传动系统中的3 类滚动轴承的滚动体与外圈接触负荷仿真结果和滚动体转速仿真结果如图13 所示.

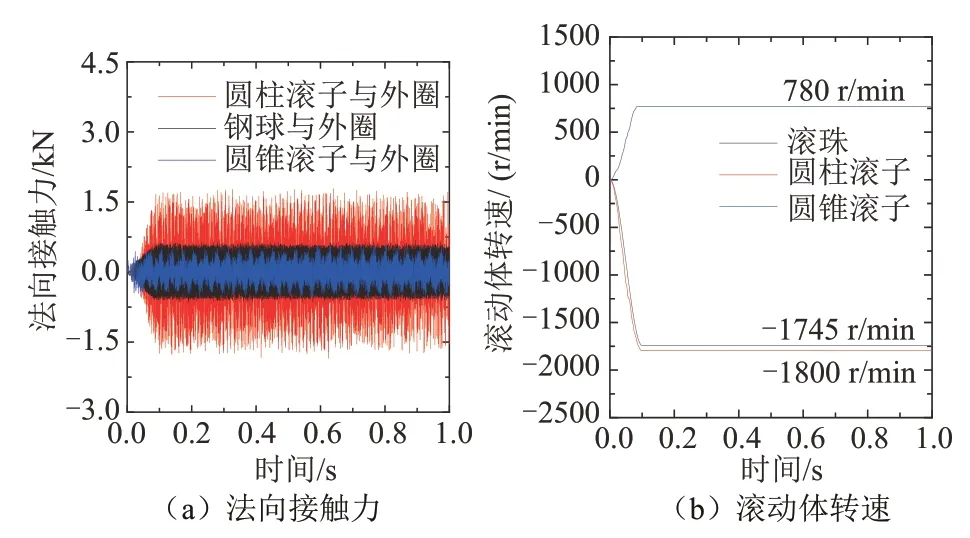
图13 滚动体与外圈接触力和转速Fig.13 Contact force and rotational speed of rolling element and outer ring

由图13 可知，圆柱滚子与外圈的法向接触力仿真结果最大值为1 480 N；滚珠与外圈的法向接触力仿真结果最大值为630 N；圆锥滚子与外圈的法向接触力仿真结果最大值为585 N.依据图13（b）可知，圆柱滚子公转速度为1 800 r/min、滚珠公转速度为1 745 r/min、圆锥滚子公转速度为780 r/min.

对于大、小齿轮处轴承外圈振动加速度如图14所示.

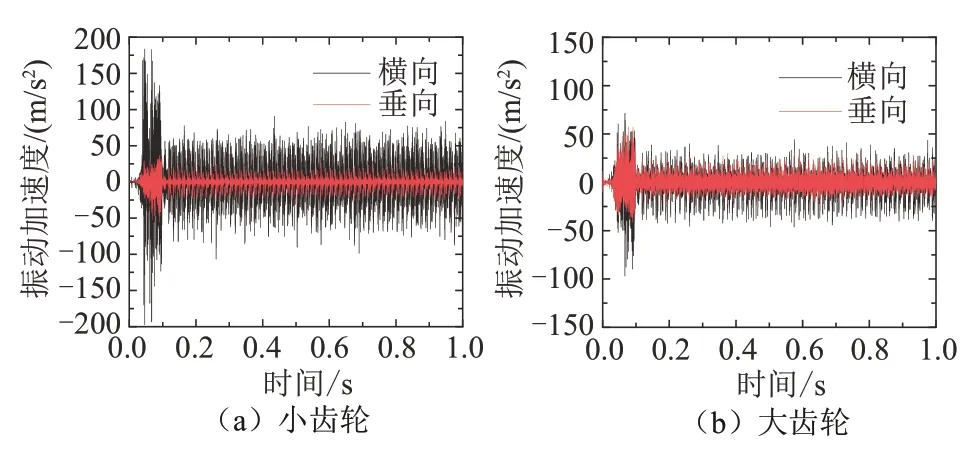
图14 大、小齿轮处轴承外圈振动加速度Fig.14 Vibration acceleration of bearing outer ring at large and small gears

由图14（a）可知，小齿轮轴承外圈横向振动加速度大于其垂向加速度，且在加速阶段0～0.1 s 时间内轴承外圈横、垂振动加速度波动较大；由图14（b）可知，小齿轮轴承外圈横向振动加速度略大于其垂向加速度.

大、小齿轮处滚动轴承保持架的质心位移在yz平面的运动轨迹，如图15 所示.

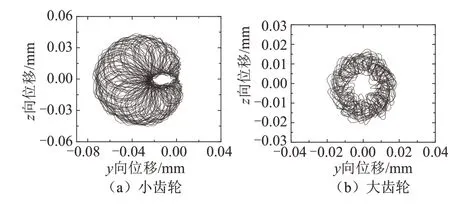
图15 大、小齿轮处轴承保持架质心位移轨迹Fig.15 Displacement track for center of mass in bearing cage at large and small gears

由图15（a）中可知，质心位置在运动过程中存在轻微偏移状况，其偏移主要发生在y方向，偏移量在0～0.04 mm，究其原因，小齿轮在运行过程中由于齿轮啮合作用而使得自身振动情形较为严重，从而引起该处轴承保持架发生偏移，但对轴承整体的运行影响较小，位移轨迹近似圆形说明该保持架仍具有一定稳定性；由图15（b）可知，大齿轮轴承的保持架质心在运行过程中位移轨迹在y、z方向均在范围0～0.02 mm 内变化，且其轨迹近似圆形说明大齿轮处轴承运行稳定性良好.对比二者可知，大齿轮处轴承保持架运行状态要优于小齿轮处轴承保持架.

滚动轴承处的仿真结果与计算结果对比结果见表2 所示.

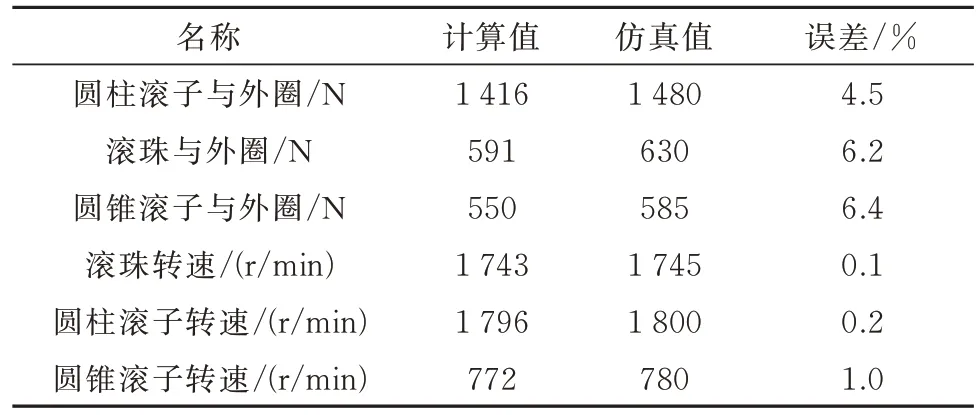
表2 齿轮啮合仿真结果对比Tab.2 Comparison of simulation results during gear meshing

根据滚动轴承处的仿真结果与计算结果对比，滚动体与外圈间的法向接触力计算值略小于仿真结果，其原因在于计算过程忽略了滚动体与内外圈间的冲击与碰撞作用，但在实际工况中滚动体与内外圈间存在冲击与碰撞作用，并且齿轮箱传动系统在实际运营过程中，滚动轴承中的滚动体与内外圈间均存在着冲击与碰撞作用，因此计算结果值应小于仿真结果值.

齿轮箱传动系统传动部件与箱体的振动加速度处于匀速状态下的均方根值，即0.1～1.0 s 范围的均方根值如图16 所示.

由图16 可知，对于齿轮箱传动系统各部件的横向振动加速度均方根值，小齿轮轴承外圈处横向加速度均方根值表现最为突出，其大小为21 m/s2，其次为小齿轮处、其大小为20 m/s2，大齿轮横向振动加速度均方根值最小；对于垂向振动加速度均方根值而言，小齿轮垂向加速度均方根值表现最为突出，其大小为11 m/s2，其次为大轴承外圈处，其大小为6 m/s2，大齿轮垂向振动加速度均方根值最小.

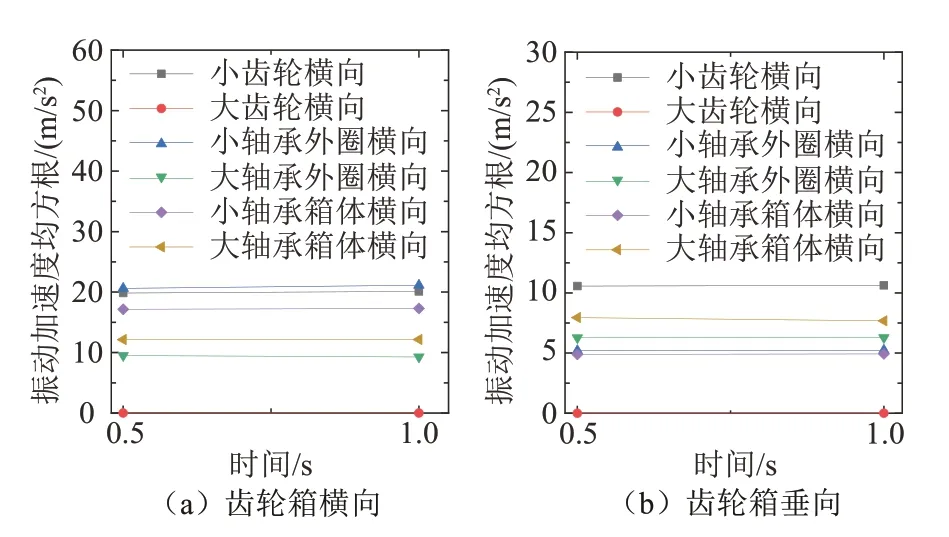
图16 齿轮箱横、垂向振动加速度均方根Fig.16 Gearbox horizontal and vertical vibration acceleration root mean square

综上所述，通过对滚动轴承内部接触力的仿真结果与计算结果的对比分析，得出了滚动轴承内部接触力能够反映出实际工况下的内部接触的载荷特征，并且滚动体的公转速度也能够较为准确地表达出实际工况下应有的公转速度大小.在齿轮箱传动系统中小齿轮端与滚动轴承联合作用下对箱体的振动影响较大，其次为大轴承滚动作用下对箱体的振动影响较大.

5 箱体振动特性与实验验证

5.1 实验台结构与组成

高速动车滚振实验台结构组成如图17 所示.主要包括单轮及驱动系统、模拟构架、垂向加载作动器、加载框架、轨道轮组、轨道轮激振器、轨道轮驱动系统、冲角调节装置及机座等部分.

图17 高速动车滚振实验台Fig.17 High-speed train rolling vibration test bench

利用该试验台可实现传动系统的正向和反向驱动，为使工况更贴近实际，实验采取电机驱动小齿轮方式，并应用垂向加载作动器对转向架施加垂向载荷，其载荷大小根据实验工况设定.

5.2 箱体测点

布置在齿轮箱箱体上的传感器测点位置，位于小齿轮箱体处轴承的正上方，其测点为A；大齿轮箱体处轴承的正上方，其测点为B.A、B 位置如图18所示.

图18 传感器A、B 位置Fig.18 Sensor A,B positions

为准确探析齿轮箱箱体在高速运行工况下，因内部激励而引发的振动情形，本次实验将动车运行速度设置为300 km/h 匀速工况，传动系统驱动方式为电机驱动，实验采用的转向架轮对为正常无故障轮对，实验作动器垂向静载荷设置为5 t，其中5 t 为单轴所承受车体及车下悬挂构件质量.

5.3 实验与仿真结果对比分析

通过Ansys Workbench 有限元软件得到了齿轮箱箱体在约束工况下的模态频率与振型，其中箱体的约束方式为：在小齿轮箱体的上下两侧通过固定支承方式对箱体进行约束；在5 个轴承座孔中心位置添加5 个远程点，并通过命令流方法分别对5 个轴承座孔处添加刚域以及求解箱体模态.最终在约束条件下的箱体模态仿真结果前8 阶见表3 所示，其振型前4 阶如图19 所示.

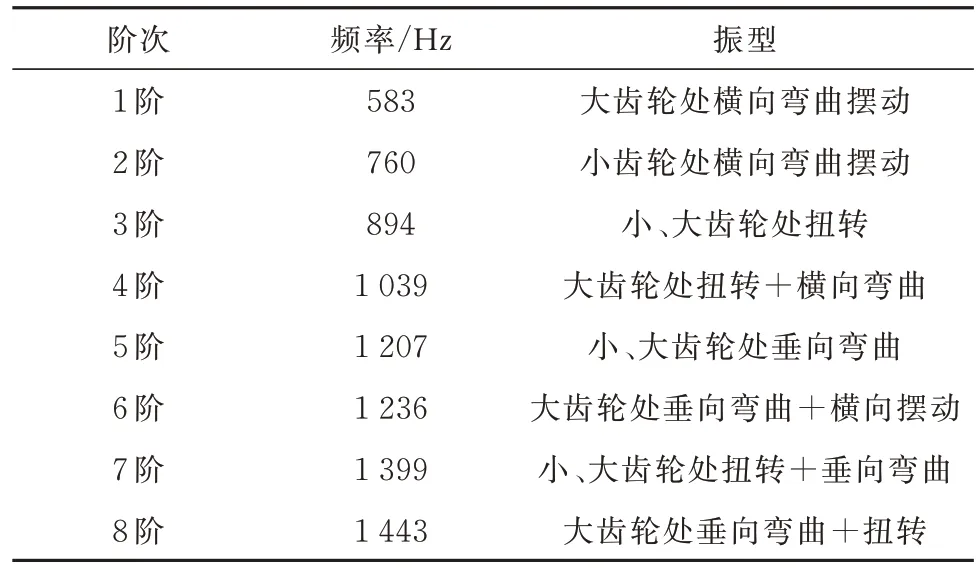
表3 齿轮箱箱体模态仿真频率Tab.3 Modal simulation frequency of gearbox case

由表3 和图19 可知，前8 阶箱体约束模态频带在500～1 500 Hz 范围内，在各阶振型中相对较为敏感部位有小齿轮箱体处、大齿轮箱体顶部及底部，而大轴承座孔处振型表现不明显.

图19 箱体约束模态振型Fig.19 Box constrained mode shape

齿轮箱箱体A、B 测点处振动加速度的实验与仿真结果如图20、图21 所示.

由图20、图21 可知，A、B 两测点处时域的轴向与垂向振动加速度有着较好的一致性，并且实验结果值略大于仿真结果.对于A、B 两测点处垂向频域加速度仿真与实验结果见表4 所示.

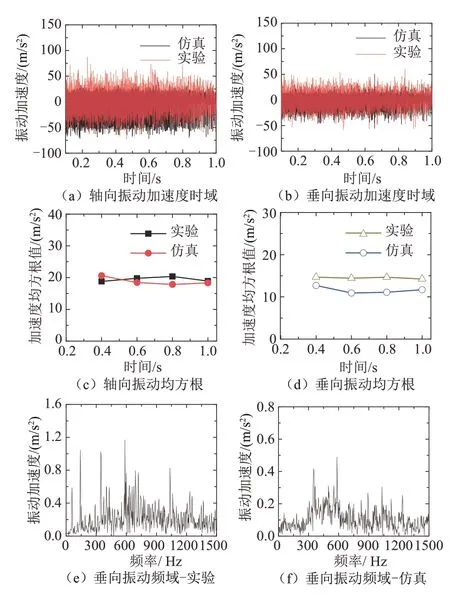
图20 A 测点时域、频域下实验和仿真结果对比Fig.20 Comparison of experimental and simulation results at test point A in time domain

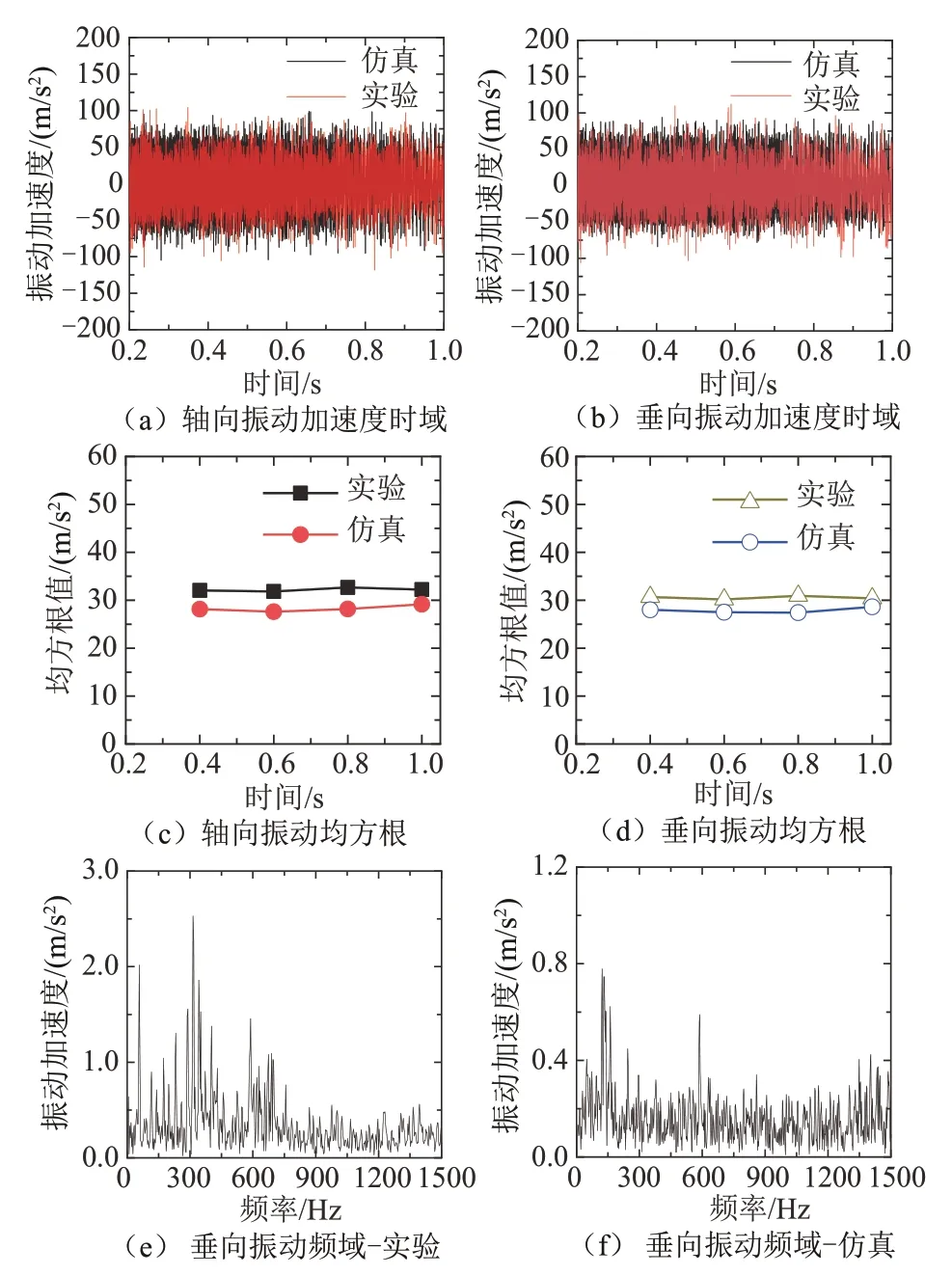
图21 B 测点时域、频域下实验和仿真结果对比Fig.21 Comparison of experimental and simulation results at test point B in time domain

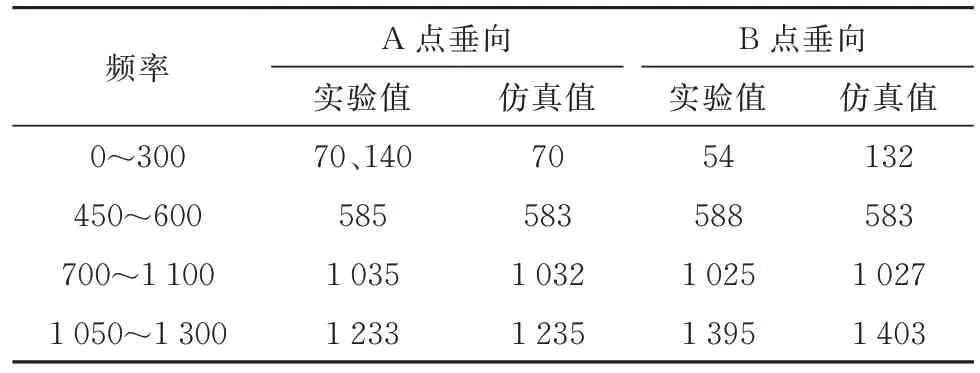
表4 A、B 两测点实验与仿真结果频域主频点Tab.4 Experimental and simulated frequency domain result values of two measuring points A and B Hz

根据箱体模态结果可知，A 测点处垂向加速度频域结果中585 Hz、1 035 Hz 及1 233 Hz 分别对应于箱体模态固频的第1 阶、第4 阶以及第6 阶.仿真结果中583 Hz、1 032 Hz 及1 235 Hz 分别对应于箱体模态固频的第1 阶、第4 阶以及第6 阶；B 测点处垂向加速度频域结果中588 Hz、1 025 Hz 及1 395 Hz 分别对应于箱体模态固频的第1 阶、第4 阶以及第7 阶.仿真结果中583 Hz、1 027 Hz 及1 403 Hz 分别对应于箱体模态固频的第1 阶、第4 阶以及第7 阶.

综上所述，通过对齿轮箱传动系统的实验与仿真，发现了齿轮箱箱体振动特性实验结果与仿真结果在时域和频域中均有较好的一致性，并且箱体的振动敏感主频点为模态固频第1 阶583 Hz 与第4 阶1 039 Hz，由此验证了仿真结果的可信度.

6 结论

1）齿轮啮合力与滚动轴承法向接触力的仿真结果值与理论结果值具有较好的一致性.

2）在齿轮箱传动系统中小齿轮端与滚动轴承联合作用下对箱体的振动影响较大，其次为大轴承滚动作用下对箱体的振动影响较大.

3）测取了箱体仅在传动系统内部激励工况下的箱体振动加速度，并与仿真结果进行对比验证，发现了仿真结果与实验结果具有较好一致性.证明了该模型能够反映实际工况下箱体的振动响应情形.