承压水层圆形基坑悬挂式止水帷幕涌水量解析

吴杰，李鹏飞，贾嘉陵，孔恒，郭彩霞，郭飞

（1.北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124；2.北京市政建设集团有限责任公司，北京 100048）

近年来，随着国家经济不断增长，城市化水平不断提高，城市中出现越来越多的超高层建筑与大规模地下综合体，导致深基坑的数量急剧增加［1-3］.因为深基坑底部往往存在承压水层，当承压水层的水头较高时，需要采取降水减压措施来避免坑底突涌及结构整体上浮等问题［4］.现有的地下水减压措施中，抽水井配合悬挂式止水帷幕组成的“墙-井”截排减压系统［5-6］因具有控水效果好、施工简单快速等优点被广泛采用.在“墙-井”系统的设计过程中，为了合理设计减压井群的总抽水量或总疏干量，需准确计算出不同坑底水头设计值下悬挂帷幕基坑内的涌水量［7］.目前，国内外学者综合采用理论推导、数值模拟、室内模型试验等方法对悬挂帷幕基坑内涌水量展开研究.王军辉等［8］通过分析悬挂式止水帷幕影响下渗流场中绕流和非绕流两个区域的渗流特征，对大井法公式进行修正并推导出含止水帷幕条件下潜水和承压水的涌水量计算公式.张志红等［9］针对基坑内外流网分布规律，根据地下水动力学原理推导出深厚潜水层中悬挂式止水帷幕圆形基坑的涌水量计算公式.李瑛等［10］将悬挂帷幕基坑按面积等效为井壁进水的大直径承压完整井，推导出基坑截排减压降水涌水量计算的简化公式，并与数值计算结果进行对比验证得出结论：简化公式在帷幕插入比大于0.6、基坑半径与承压含水层厚度比值小于2.0 时具有较高精度.肖铭钊等［11］通过对武汉长江隧道武昌盾构井基坑水文地质条件的分析，建立三维渗流有限元模型，并对悬挂式止水帷幕深基坑降水过程进行数值模拟计算.在基坑总抽水量一定的条件下，定量分析了止水帷幕插入深度与基坑内外水头值的相互关系.李光明等［12］依托天津某地铁换乘车站基坑降水工程，通过现场抽水试验数据反演出数值模型的地层参数，然后利用有限差分法对悬挂帷幕基坑降水过程中坑内涌水量进行数值模拟计算.张邦沛等［13-14］通过室内模型箱实验探究帷幕插入深度对基坑内涌水量的影响，并提出了止水帷幕插入深度合理取值范围，为实际工程中止水帷幕设计参数提供参考.

综上所述，现有理论解析求解悬挂帷幕基坑涌水量与实际情况及数值模拟结果对比存在较大误差，仅在某些特定r0/M、L/M范围内具有较好的精度（r0圆形基坑半径，L为止水帷幕插入深度，M为承压含水层厚度），原因是坑内等效渗径长度取值不合理.现有数值方法对悬挂帷幕基坑的研究大多是基于某些特定工程，结果的精确性依赖于特定的边界条件的选取［8，11-12］，对工程的指导不具有普适性.在此背景下，本文应用地下水动力学原理求解出承压水层悬挂式止水帷幕圆形基坑的涌水量，引入基坑渗径影响系数，并提出其确定方法.经对比显示本文解析结果与数值模拟结果及实测数据取得了较好的一致性.

1 涌水量计算的理论解析

以圆形基坑中轴线为z轴，基坑径向为r轴，中轴线与含水层底板交点选为原点建立柱坐标系.根据地下水动力学原理，建立如图1 所示的承压水地层悬挂式止水帷幕基坑数学模型.其中：H为承压水头高度，r0为圆形基坑半径，R为基坑抽水影响半径，h0为止水帷幕底部中轴线处水头等值线的水头值，D（z）为止水帷幕外侧壁处水头分布函数，Hd为坑内水头设计值，Hw为坑外承压含水层顶板最大降深处水头值，L为止水帷幕在插入承压含水层的长度，M为含水层的厚度.

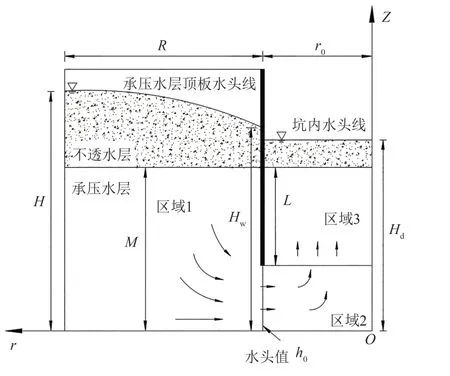
图1 承压水地层悬挂式止水帷幕基坑计算模型Fig.1 Calculation model for pit with suspended waterproof curtain in confined aquifer

本模型忽略止水帷幕厚度，假定坑内渗流过程为三维稳定流，坑内的水头线均为水平线.根据实际工程经验与现有研究成果［10，12］，可将渗流区域分为坑外（区域1）、坑内止水帷幕下方（区域2）、坑内竖直渗流区（区域3）3 部分.由于止水帷幕的存在，区域1 内水流绕流进入区域2，且帷幕正下方水流流向均为水平.然后水流在区域2 内转向，沿竖直方向流入区域3.根据渗流连续性原理可知3 个区域内流量相同，即Q1=Q2=Q3=Q.

计算区域渗流场内任意一点的总水头h（r，θ，z）与角度无关，即各点总水头可以表示为h（r，z）.渗流区域内的边界条件为

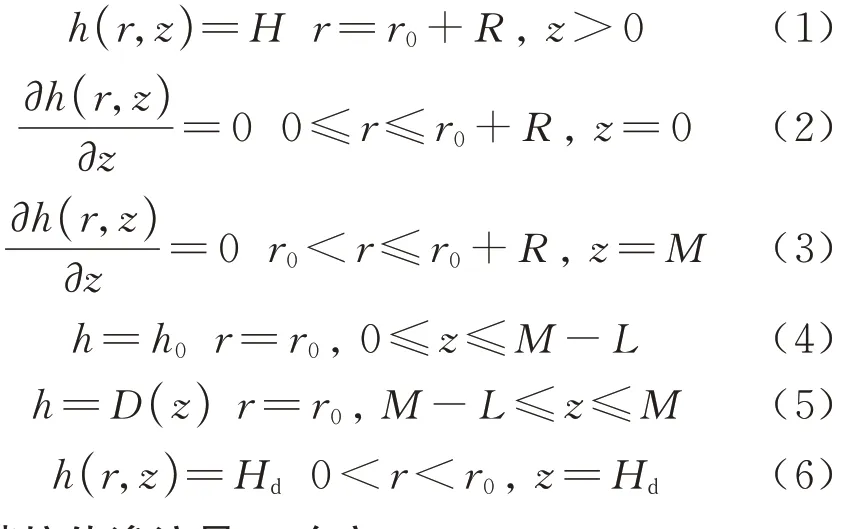
1.1 基坑外渗流量Q1确定

根据达西定律，承压含水层内任意一点的水平渗流速度为

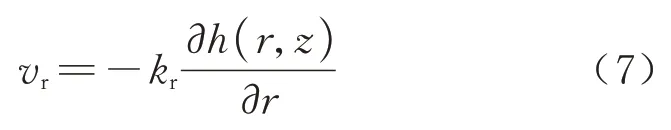
式中：kr为承压含水层内水平渗透系数.在区域1 中，单位时间内过任一断面的流量为

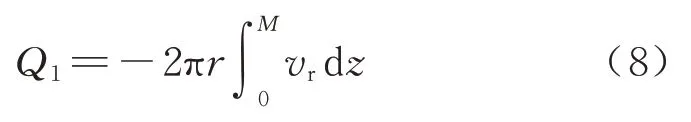
将式（7）代入式（8）可得过区域1 单位时间内任一断面流量表达式

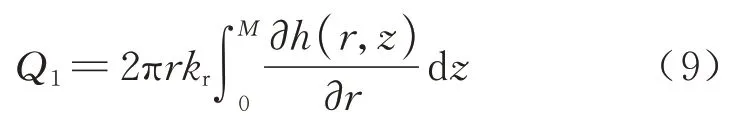
文献［9］中给出了在M－L＜z＜M范围内止水帷幕外侧水头分布规律，结合边界条件式（4）和式（5），可以分别得到D（z）和Q1为

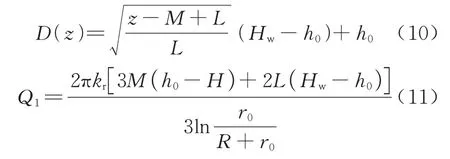
1.2 基坑内涌水量Q2和Q3确定

水流在渗流区域内的最短渗流路径为

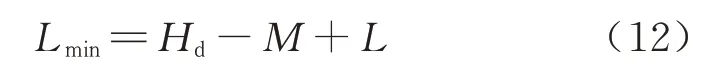
最长渗流路径为

若坑底水头线位于上部不透水层的底板上方，即Hd＞M，则式（12）和式（13）中Hd可以用M代替.利用达西定律求解基坑内涌水量时，现有理论解析大多是将基坑内的等效渗径长度定为（Lmax+Lmin）/2［9，15］，或直接假定2Lmin［8，10］，这两种情况计算得到的坑内涌水量只在r0/M、L/M的某些特定区间内较为合理.实际上，基坑内等效渗径长度的取值应随r0/M、L/M的不同而变化，直接用（Lmax+Lmin）/2 或2Lmin替代是不合理的.为了精确计算各工况下基坑内涌水量的值，引入可以体现等效渗径长度随r0/M、L/M变化的渗径影响系数α，并通过数值实验探究变化规律.基坑内等效渗径的长度可以表示为

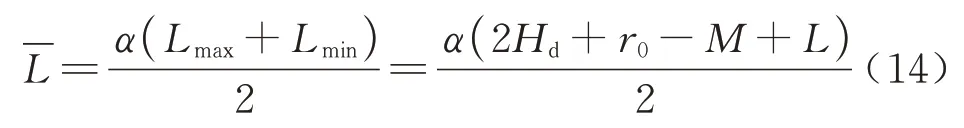
其中α为r0/M、L/M的函数，即

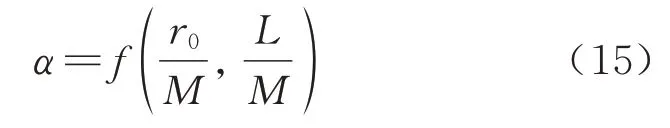
区域2 和区域3 内的涌水量为

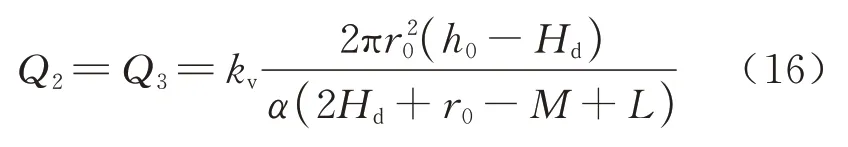
式中：kv为垂直渗透系数.

1.3 承压含水层顶板处最大降深水头Hw确定

在忽略止水帷幕厚度的条件下，水流沿止水帷幕绕流时，通过帷幕内侧的水头损失要大于通过帷幕外侧的水头损失.根据现有实验数据与理论研究成果［8-9，13］，潜水含水层各工况下水流通过帷幕内侧的水头损失约占绕流总损失的2/3 左右.而无论在承压水层还是潜水层中，水流沿止水帷幕绕流时的方向和特征都是一致的，所以将此结论应用于承压水地层中，帷幕底端等水头线水头值h0可以表示为

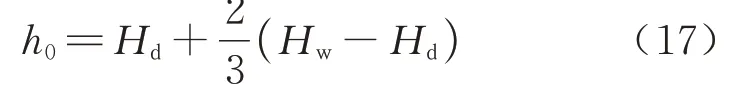
将式（17）带入式（11），再根据渗流连续性原理，可以求得坑外承压含水层顶板处最大降深水头Hw分布函数

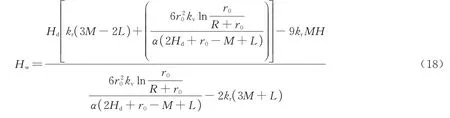
将式（17）和式（18）代入式（16）即可求得圆形基坑涌水量.

2 渗径影响系数探究

根据对称性，建立圆形基坑渗流计算数值模型，如图2 所示.数值模型的依托工程土层特点为砂黏混合地层，含水层主要为细砂.计算取渗透系数kr=kv=5×10-6m/s，承压层水头高度H=30 m，坑内水头设计值Hd和含水层的厚度M均为10 m.

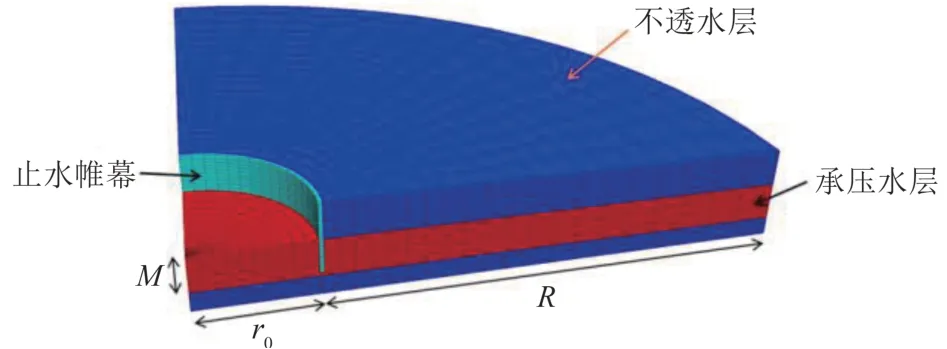
图2 悬挂式止水帷幕圆形基坑数值模型Fig.2 Numerical model for circular pit with suspended waterproof curtain in confined aquifer

选取r0/M=1、3、5、7、9 作为试验工况，并基于此探究系数α变化规律，剩余r0/M=2、4、6、8、10 作为验证工况.图3 所示为基坑涌水量随r0/M、L/M的变化规律.由图3（a）可知，L/M对基坑涌水量有较大影响.随着L/M的增大，基坑涌水量不断减小，且当基坑直径较小时（r0/M=1），Q与L/M呈线性关系；其他情况下，Q随L/M的增大，先线性减小，后指数形式减小.在L/M相同的情况下，随着r0/M的增大，基坑涌水量不断增大，但增大速率不断减小.由图3（b）可知，当基坑尺寸较大时，在较大插入比下（L/M=0.9），基坑内涌水量依然很大，要有效控制涌水量，需要加大插入比形成落底式止水帷幕.

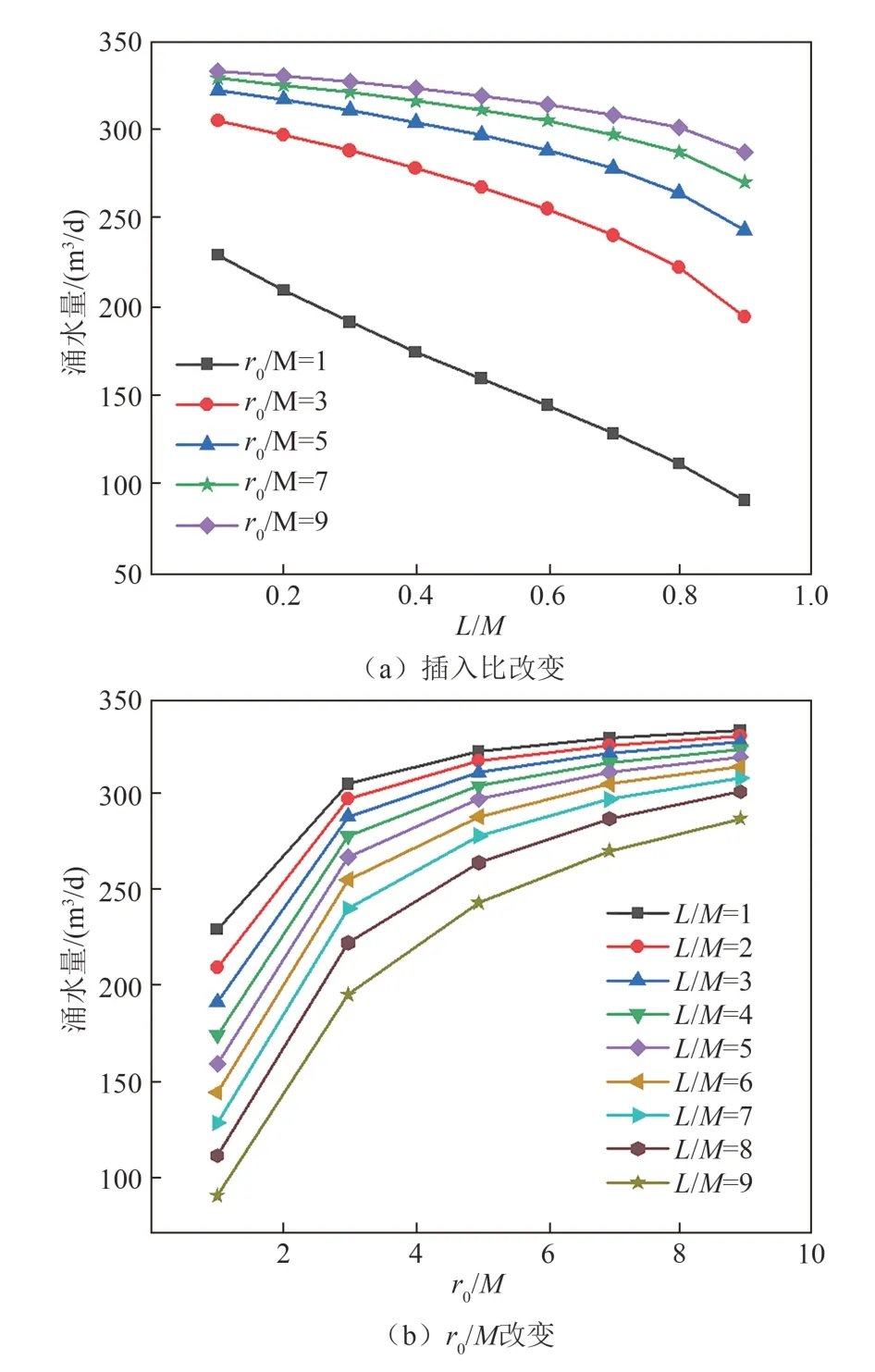
图3 涌水量随r0/M 以及插入比改变的变化关系Fig.3 Relationship between the variation of water inflow with r0/M and that of insertion ratio

α随r0/M、L/M的变化规律见图4.由图4 可知，r0/M、L/M对α均有不同程度的影响，且L/M的影响更大.如果不考虑L/M对等效渗径的影响，取α恒等于1，各工况大致对应图4（a）中L/M为0.7～0.8 时的条件，即此时涌水量理论计算结果才与数值结果吻合.随着L/M的增大，α先近似线性增大，后指数增大，近似以L/M=0.7 为分界点.随着r0/M的增大，α先增大后减小，拐点为r0/M=3.

首先根据图4（a）中α的变化特点建立α与L/M的函数关系

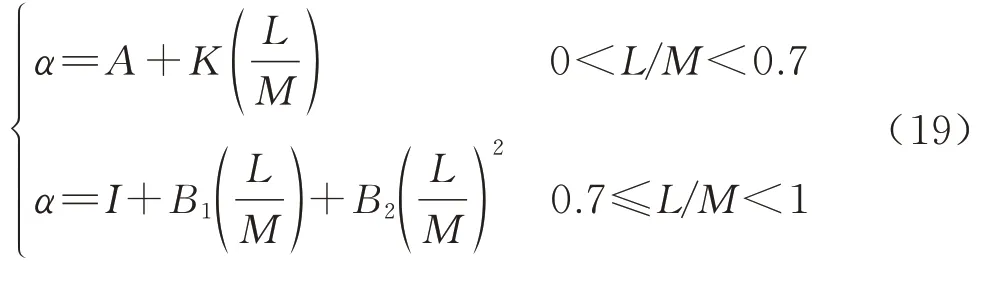
式中：A为一次函数的截距；K为一次函数的斜率；I为二次多项式截距；B1为一次项系数；B2为二次项系数.将式（19）与图4（a）中的曲线拟合，得到不同r0/M工况下的参数A、K、I、B1、B2.然后，再建立r0/M与系数α的关系，假设各参数为随r0/M变化的一次函数为

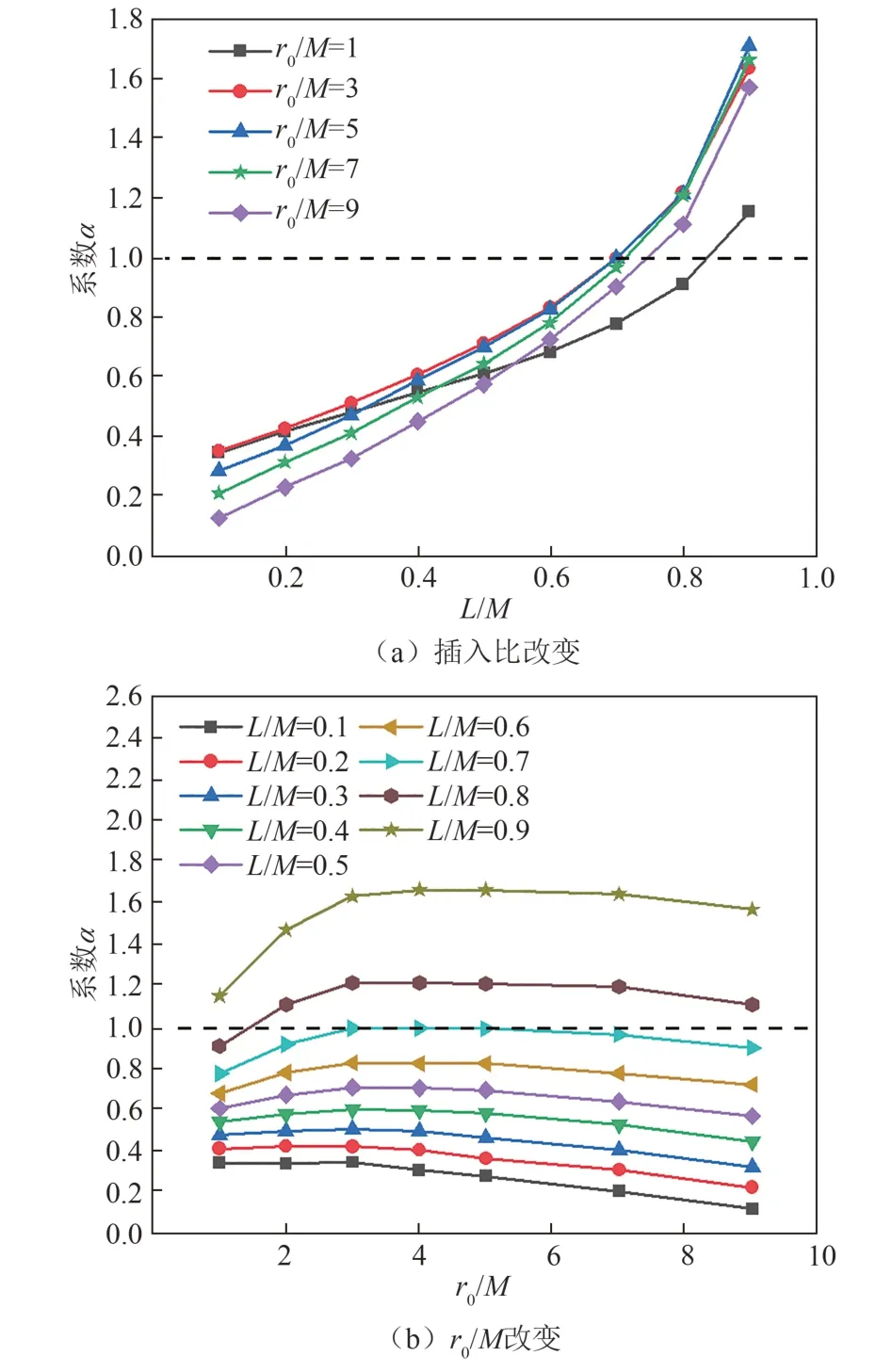
图4 α随r0/M 以及插入比改变的变化关系Fig.4 Relationship between the variation of α with r0/M and that of insertion ratio

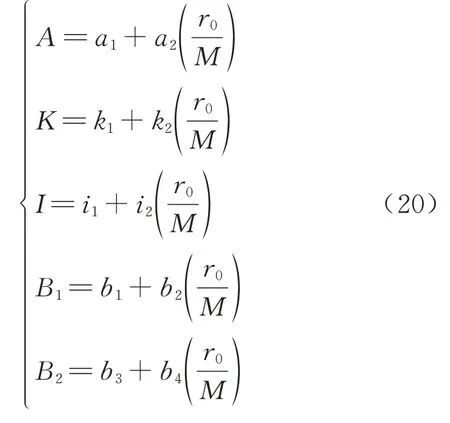
其中：a1、a2、k1、k2、i1、i2、b1、b2、b3、b4均为一次函数的参数，将不同r0/M工况下A、K、I、B1、B2的取值代入式（20），即可解得式中一次函数的参数值.再将式（20）代入式（19），得到系数α分段函数为

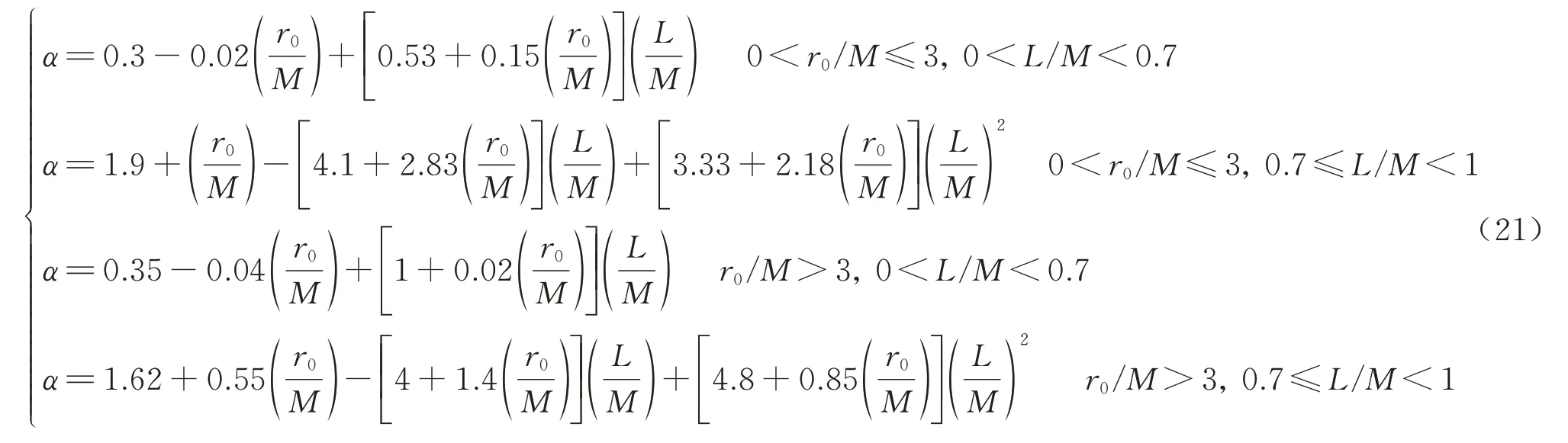
3 验证及分析

3.1 算例验证

图5（a）为验证工况基坑涌水量解析解与数值解计算结果对比.由图5（a）可知，本文解析解与数值模拟结果吻合，涌水量随L/M变化规律与图3（a）中分析的结论一致.两者在r0/M=2、4、6、8、10工况下最大相对误差分别为4.5%、2.3%、1.6%、1.4%、1.7%，均小于5%.图5（b）为r0/M=4、6、10工况Hw解析解与数值解计算结果对比.由图5（b）可知，解析解与数值模拟结果变化规律吻合，Hw随着L/M增加而增大.当L/M＞0.7 时，两种计算方法得到的Hw基本相同.0＜L/M＜0.7 时，两种方法计算结果变化趋势相同，解析解略小于数值解.3 种工况对应的最大相对误差分别为：3.3%、4.5%、4.2%，均小于5%.

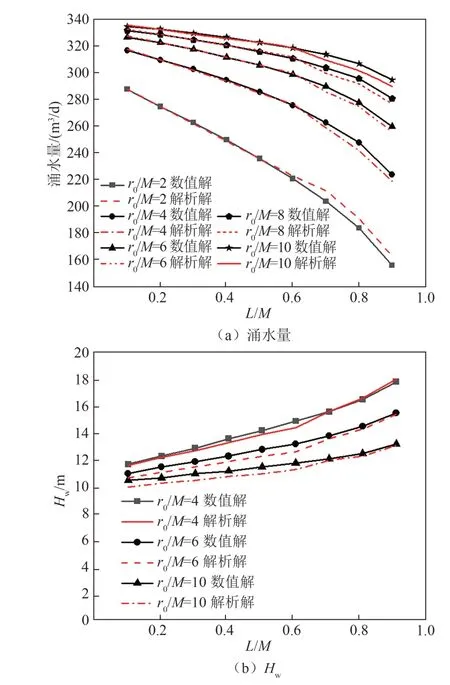
图5 不同面积基坑的涌水量与Hw计算结果对比Fig.5 Comparison of calculation results of water inflow and Hw under different areas of foundation pit

3.2 补充工况验证

为了进一步验证推导公式的准确性与普适性，分别改变数值算例中的土层渗透系数、承压含水层厚度、基坑内外水头差H－Hd，并计算不同r0/M、L/M时的基坑内涌水量.图6 为这3 种因素改变时，r0/M为2、4 工况下的涌水量解析解与数值模拟结果对比.由图6 可知，涌水量解析解与数值模拟结果变化规律吻合.在任一工况下，涌水量随L/M的变化都是先线性减小，再呈指数形式减小.在其他条件不变时，涌水量分别随着土层渗透系数、承压含水层厚度、基坑内外水头差的增大而增大.当3 种条件分别改变时，解析解与数值解的最大相对误差出现在r0/M=2、kr=kv=1×10-5m/s 时，r0/M=4、M=20 时以及r0/M=2、H－Hd=15m时，其值分别为4.5%、4.3% 以及3.8%，均小于5%.在不同工况下，基坑内涌水量数值模拟结果与本文解析解基本吻合，对比结果最大相对误差在可接受范围之内，可以证明推导公式具有较高的精度与普适性.

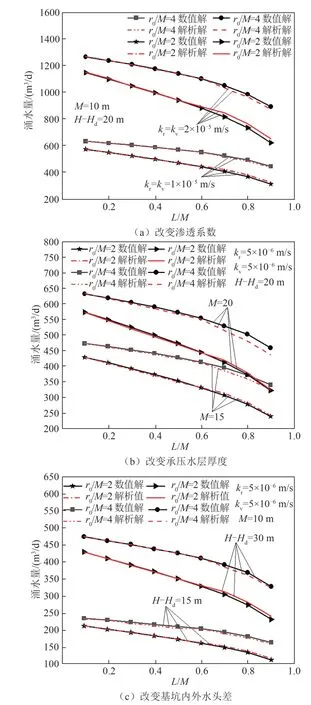
图6 补充工况的涌水量计算结果对比Fig.6 Comparison of calculation results for water inflow under supplementary conditions

3.3 解析解与工程实测数据对比

表1 为解析解与工程实测值对比.表1中Qc1与Qr分别为来源于参考文献［10］中的解析解涌水量计算值与既有工程现场实测涌水量，Qc1未考虑渗径影响系数，Qc2为对应工况下本文解析解涌水量计算值.Qj为不考虑止水帷幕影响的计算涌水量，由规范［16］计算得到.由表1 可知，Qc1与Qc2都远小于规范解，说明悬挂止水帷幕可以有效降低基坑涌水量.比较Qc1与Qc2可知，除案例乙中两者值接近，其他情况Qc2都远比Qc1更接近实测值，表明渗径影响系数对基坑涌水量计算结果有较大影响.考虑渗径影响系数的计算结果更准确，而且Qc2总是略大于实测值，实际工程中用于计算降水井抽水量也是偏安全的选择.

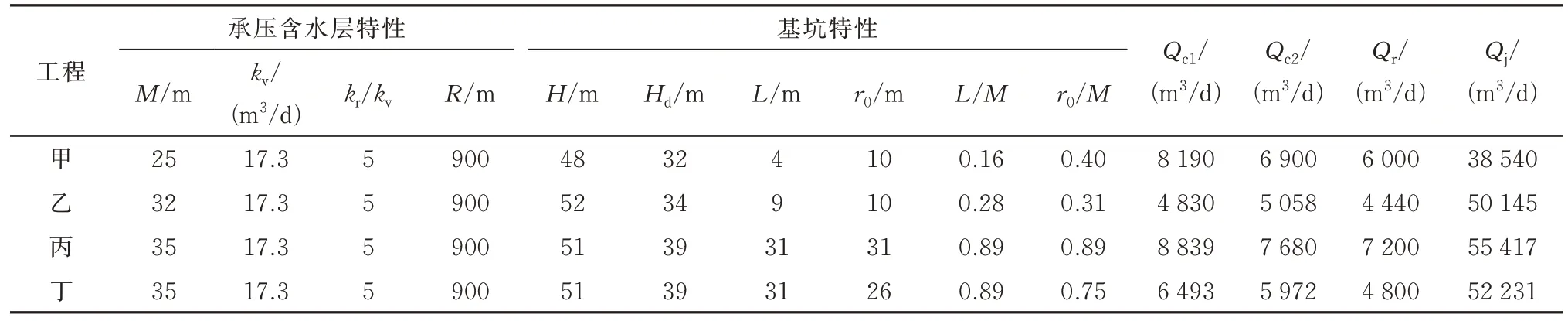
表1 解析解与工程实测值对比Tab.1 Comparison of analytical solution and measured filed values

3.4 基坑尺寸与悬挂式止水帷幕控水效果关系

由图3 与图5 综合分析可知：无论是解析解还是数值模拟结果，在L/M一定时，涌水量随着r0/M的增大而增大，但涌水量增加的速率显著减小，且涌水量随L/M的变化越来越平缓.定义Qi1、Qi9为r0/M=i时（i=1，2，…，10），L/M=0.1和L/M=0.9 对应的涌水量，η为Qi1和Qi9的差值与Qi1的比值.图7（a）为η随r0/M的变化关系，可以反映悬挂帷幕对不同尺寸基坑的止水效果，η值越大，证明止水效果越好.由图7（a）可知，悬挂帷幕止水效果随r0/M的增大而降低，当0＜r0/M＜5 时，止水效果随r0/M的增大显著降低，r0/M＞5 以后，η值已经远小于初始值且不再显著变化.图7（b）为较大插入比时（L/M=0.9），Hw随r0/M的变化关系，Hw越小则说明坑内降水对坑外承压水位的影响越大.

图7 L/M=0.9时η与Hw随r0/M 变化Fig.7 Relationship between η and Hw with r0/M when L/M=0.9

随着r0/M增大，坑内降水对坑外承压水位的影响增大，r0/M＞5 以后，Hw值已经远小于坑外初始水头（H=30 m），且与区间0＜r0/M＜5 相比不再显著变化.止水帷幕控水效果随着r0/M增大而降低，从止水效果（随L/M的增加，坑内涌水量显著减小）和保护水资源（坑内降水对坑外水位影响较小）两方面考虑，当基坑尺寸较大时，应当考虑选用能切断基坑内外水力联系的落底式止水帷幕以达到良好的控水效果.

4 结论

1）对于承压水地层中悬挂式止水帷幕基坑涌水量的解析模型，渗径影响系数取值对计算结果影响很大，应根据基坑半径、承压水层厚度、悬挂式止水帷幕插入承压水层厚度等因素综合确定.

2）基坑半径与承压水层厚度的比值（r0/M）、悬挂式止水帷幕插入承压水层厚度比（L/M），这两个参数对渗径影响系数α的影响最为直接和显著，且r0/M=3和L/M=0.7 是二者影响分界点，本文通过数值模拟正反分析分别给出了4 种情况下α的计算公式.

3）当选用悬挂式止水帷幕作为地下水控制措施时，控水效果会随着r0/M的增大而降低，当基坑尺寸较大时，建议选取落底式止水帷幕，达到切断基坑内外水力联系的目的.