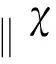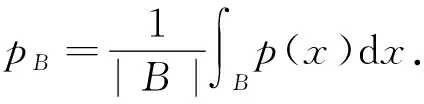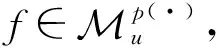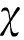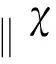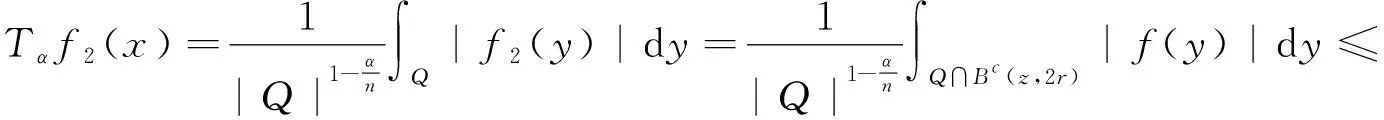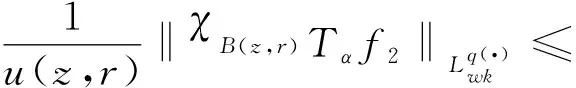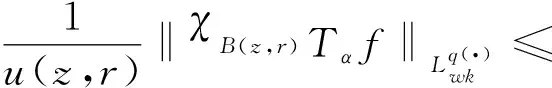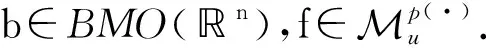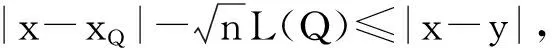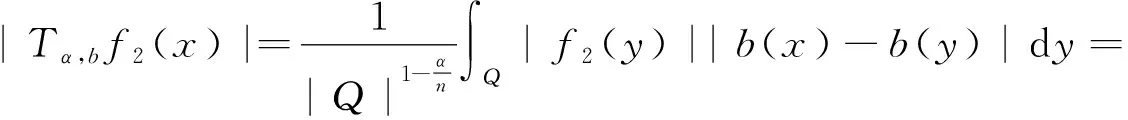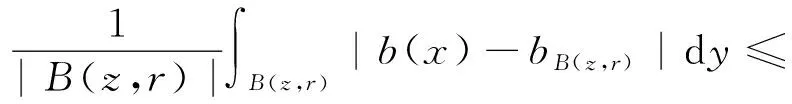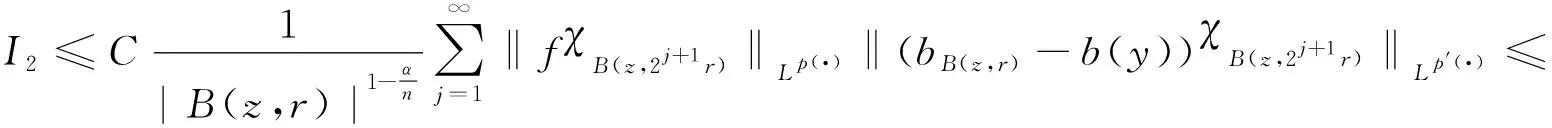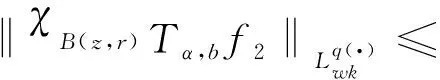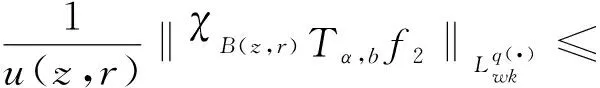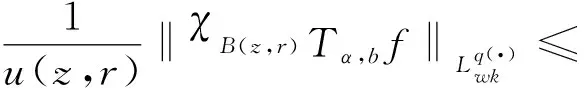变指标Morrey空间上分数次极大算子及交换子的弱型估计
徐 博,陶双平
(西北师范大学数学与统计学院,甘肃 兰州 730070)
1 主要结果
设0≤α (1) 其中Q为n中的方体.给定一个局部可积函数b,由b和Tα生成的交换子定义如下: (2) 给定可测函数p(·):n→[1,∞),变指标Lebesgue空间Lp(·)定义为 其上的Luxemburg-Nakano范数为 定义1[3]设p(x)∈L∞,1 那么称u为Lp(·)(n)意义下的Morrey权函数,用Wp(·)表示所有满足上述条件的Morrey权函数的集合. 定义2[3]设p(·):n→[1,∞),u(z,r)∈Wp(·).变指标Morrey空间n)定义为 定义3[8]设p(·):n→[1,+∞).若存在常数C>0且p∞∈,满足 (3) (4) 对于任意p(·):n→[1,∞),定义 本文的主要结果如下: 定理1 设0<α (5) 所定义.若存在常数C1>0,使得∀z∈n和r>0,u满足 (6) 定理2 设b∈BMO(n),设0<α (7) 引理1[4]若0<α 引理2[9]设b∈BMO(n),0<α 引理3[10]设0<α 引理4[11]设p(·):n→[1,∞)为全局log-Hölder连续,k为正整数,B⊂n,则对任意b∈BMO(n),j,i∈Z且j>i,有 其中B=B(x,r),Bi=B(x,2ir). 引理5[12]设p(·):n→[1,∞)满足(3)和(4)式,1=p-≤p+<∞,则存在常数C≥1,使得对任意球B,有 引理6[13]设p(·):n→[1,∞)满足(3)和(4)式,则存在常数C,D>0,使得对任意球B,有 (8) 注意到存在常数C>0,使得对任意z∈n且r>0,有 因此, (9) 由(6),(8),(9)式得 由引理6和(5)式,得 其中C,D>0且与z,r均无关.因此 则有 因此,由拟落数的定义,有 对z∈n且r>0取上确界,得 由引理2,得 进一步,利用(7)和(9)式得 对于I1,由广义Hölder不等式和引理3,有 由引理4和引理5得 因此, 对于I2,由引理4和广义Hölder不等式,有 结合I1,I2的估计,有 进一步,由(7)式得 因此,由拟范数的定义,有 对z∈n且r>0取上确界,得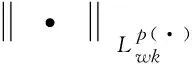
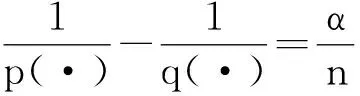
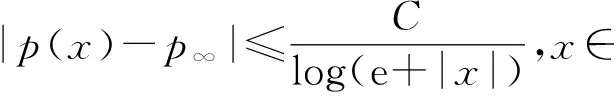
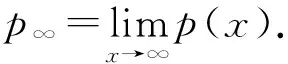
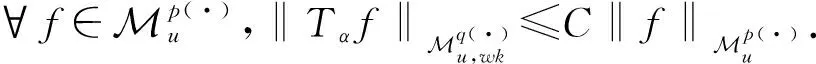
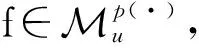
2 定理的证明