成批到达排队系统在高校图书馆流通管理中的应用

曹学云

(安徽工业大学 图书馆，安徽 马鞍山 243032)

一、排队论在图书馆管理中的应用研究文献综述

在日常生活中，排队现象是很常见的，比如在超市收银台、银行服务台、火车站售票厅，都会看到排队现象。排队论也称随机服务系统理论，是为解决排队和设备闲置之间的矛盾而发展起来的一门学科。排队系统由顾客和服务台构成，其中顾客是被服务的对象，服务台是进行服务的设备。排队系统有三个组成部分，分别是输入过程、排队规则及服务机构。输入过程是描述顾客的来源以及顾客是按怎样的规律到达排队系统的。排队规则有先到先服务、后到先服务、有优先权的服务等。服务机构主要是指服务台的数量，顾客是成批还是单个接受服务的，服务时间服从什么分布，服务时间是否相互独立。反映排队系统的主要特征的是性能指标，包括瞬态与稳态系统的队长，顾客在系统中的等待时间、逗留时间，系统的忙期和系统损失率等。通过对服务对象到达系统的时间及服务台的服务时间进行统计研究，得到一些性能指标的统计规律，然后根据这些规律来优化服务系统的结构或者规则，使得服务系统的某些性能指标最优，既能满足服务对象的要求，又能使排队系统的费用最少。

自从排队论这门学科形成以来，新的研究方向和研究方法层出不穷，随着现实问题的复杂多变，特别是近些年来电子计算机和通信技术的快速发展，使得排队模型也越来越复杂，引入的规则也越来越多。在各种各样的排队模型中，批量到达排队模型由于其具有较强的适用性而得到了广泛的研究。例如在生产系统中，原料的到达往往是批量到达的，通信系统中信元的传输也往往是成批的。Baily等[1]运用虚拟仿真算法研究了等待制的GIx/M/n/∞模型。Chaudhry等[2]讨论了等待制的Mx/M/n/∞模型。2007年，丛国超等[3]用概率母函数的方法求解了批量到达,多服务台排队模型队长的稳态分布、均值、顾客到达不用等候的概率。邱国新等[4]建立了M(ξ)/M/n/m排队模型，并证明了该模型的稳态存在性，给出了平均队长、平均等待队长、系统损失率和系统利用率等稳态指标的计算方法。

排队论适用于一切服务系统，特别在生产管理系统、交通系统、计算机系统、存储系统、通信系统中应用广泛，将排队理论应用到图书馆的管理中的研究也很多，例如在图书馆流通服务、藏书管理、科技查新和工作人员排班等方面。高莹莹等[5]针对图书馆服务台数量问题，运用排队论方法计算出了稳态平均队长、平均等待时间、平均逗留时间。诸葛晴怡等[6]研究了图书馆流通借阅排队系统模型和模型实例。蔡科平等[7]研究了图书馆借还服务的排队论模型，提出了采用借书和还书分离式的管理模式更为有效。蔡秋娥等[8]通过M/M/N排队模型对高校图书馆的服务系统做了相关研究，对服务台的设置进行了优化。李化祥[9]把借阅图书看作虚拟服务台，每个读者对图书的借阅申请看作是到达系统的顾客，针对书价上涨和图书馆馆藏经费紧张的矛盾，提出了应用排队理论来构建图书馆馆藏建设的数学模型。施晓军[10]以图书馆流通借还和科技查新两种服务为例，构建了相应的排队论数学模型，为提高图书馆服务质量和效率及优化图书馆资源配置提供了一种较有效的管理手段。魏红翠[11]利用排队论计算出不同时段的读者平均等待时间，结合管理人员的个人意愿，针对图书馆人员排班问题，分别建立了读者满意度最大和工作人员服务水平最高两种优化模型。

排队论在图书馆管理中的应用方面的文献，一般考虑的排队系统都是以读者为研究对象，每次只有一个顾客到达的情况。现实情况是每位读者每次需要借还的图书通常不止一本，如果以图书为服务对象，考虑成批到达的排队系统更为确切。安徽工业大学图书馆使用的汇文系统所显示的统计数据大多数都是以图书为对象的，所以我们考虑以图书为研究对象、成批到达的排队系统，对图书馆的流通管理更具有指导意义。

在当前疫情防控常态化的情况下，图书馆作为密闭空间的公共场所，对每天到馆人数进行了限制，要求读者落座阅读区域时要间隔一人，服务台借还书在排队等待的时候也需要间隔一米，同时图书馆在线上服务资源的推广服务也在不断加强，读者不断体验到数字资源的获取方式更加快速和便捷，这时服务台数量的设置是否需要改变，也是一个值得研究的问题。

本文以安徽工业大学佳山校区图书馆为例，利用成批到达的排队论理论对图书馆服务台数量的管理进行了研究，以更好地为读者服务。

二、系统模型

(一)系统描述

考虑这样的成批到达系统，即服务对象的到达不是只有一个，而是一批。

(1)顾客的到达间隔序列{τ，i≥1}相互独立，服从参数为λ的负指数分布F(t)=1-eλt，t≥0，即每批次到达间隔服从参数为λ的Poisson流，但在每一到达时刻不是到达一个顾客，而是到达一批顾客。而且每批到达的顾客数量为一个随机变量ζ，且P{ζ=k}=ck，

(2)服务台的服务是单个进行、互相独立的，顾客所需要的服务时间服从参数为μ的负指数分布。

(3)系统中有n个服务台。由于图书馆场地容纳的读者数量有限，故考虑系统的容量为m。顾客到达时，若服务台空闲就立即接受服务，否则就排队等待。如果系统内顾客已满，那么新来的顾客会立即离开。

(4)在同批次到达的顾客中，服务顺序是任意的，但在不同批次到达的顾客中，服务顺序仍然按照先到先服务的规则。

(二)模型建立

设{X(t),t≥0}表示系统的状态，即t时刻系统中的顾客数量。系统的状态空间为E=(0,1,2,…，m)。系统的状态转移如图1所示：

图1 系统的状态转移

这是一个有限状态的不可约齐次马尔科夫链，其平稳分布一定存在，其稳态方程组为：

(三)性能指标

1.流通强度。令ρ表示流通强度，ρ=λ/nμ。流通强度决定了系统的稳定状态，当ρ<1时，表示系统里面顾客数量不会无限制地增长下去，等待的顾客逐渐减少。在系统平衡状态下，研究系统的一些性能指标是有意义的。

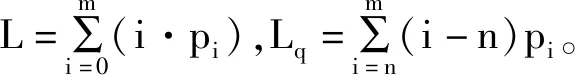
5.系统的损失率：ps=pm。

三、模型应用

1.基本模型

由于在高校图书馆中，服务的对象主要是教师和学生，他们一般会在没课的时候来图书馆借还书。本文根据安徽工业大学佳山校区图书馆汇文系统的实际借还书数据统计得出：在晚上和周末这些读者空余时间比较充裕的时间段，读者到达率是50人/小时，即λ1=50；在上午和下午大多数读者有课的时间段，读者到达率是20人/小时，即λ2=20。

在佳山校区图书馆中，由于流通量的要求，读者最多借书量为10本。根据汇文系统的统计，每批到达的读者携带图书数量ζ的概率分布如下：

P(ζ=1)=c1=0.01，P(ζ=2)=c2=0.05，P(ζ=3)=c3=0.08,

P(ζ=4)=c4=0.13，P(ζ=5)=c5=0.2，P(ζ=6)=c6=018,

P(ζ=7)=c7=0.12，P(ζ=8)=c8=0.1，P(ζ=9)=c9=0.08，

P(ζ=10)=c10=0.05。

根据统计分析，业务熟练的服务人员服务率一般为60本/小时，即μ=60。

目前图书馆内设置了2个服务台，即n=2。

由于当前疫情防控要求，到馆的读者在借还书时排队需要间隔一米，故服务台前的可供排队的场地容量只有10人，即m=10。

将上述数据代入(1)中，即可得出其稳态方程。

解出当λ1=50时，该系统在统计平衡状态下的各个状态的概率如下：

P10≈0.137，P11≈0.114，P12≈0.104，P13≈0.096，P14≈0.088，P15≈0.080，P16≈0.070，P17≈0.059，P18≈0.050，P19≈0.040，P110≈0.162。

由此可得出系统的几项主要的稳态性能指标：

(1)系统的流通强度ρ1=0.08，

(2)平均队长L1=4.57，

(3)逗留时间D1=0.0914，

(4)系统的损失率Ps1=0.162。

当λ=20时，该系统在统计平衡状态下的各个状态的概率如下：

P20≈0.181，P21≈0.121，P22≈0.106，P23≈0.096，P24≈0.086，P25≈0.076，

P26≈0.063，P27≈0.051，P28≈0.041，P29≈0.031，P210≈0.148。

由此可得出系统的几项主要的稳态性能指标：

(1)系统的流通强度ρ2=0.03，

(2)平均队长L2=4.167，

(3)逗留时间D2=0.20835，

(4)系统的损失率Ps2=0.148。

(二)数据分析

由于不同时段，读者到达率不同，会造成不同时段的工作人员的工作强度差异较大，对不同班次的工作人员有失公平。一般的做法是不同时段开设不同数量的服务台个数以优化管理。但是在本文中，顾客到达率不同的情况下，即λ1=50和λ2=20，系统的流通强度分别为ρ1=0.08和ρ2=0.03，平均队长分别为L1=4.57本和L2=4.167本，逗留时间分别为D1=0.0914小时和D2=0.20835小时，系统的损失率分别为Ps1=0.162和Ps2=0.148。从计算结果上看，不同的到达率，并没有给系统的其他性能指标值造成太大的差异，对于到达的读者来说，两种平均队长，也就是排队等待的人数都是可以接受的，对于服务台人员来说，两种流通强度也是可以接受的。这是由于目前疫情防控常态化情况下，每天读者到馆借还书的数量很小，而且根据疫情防控的要求，图书馆场地的容纳量相对之前也变小了。数据结果显示，即使是在周末和晚上到馆人数相对较多的时候，即λ1=50，计算得出流通强度也很小，读者逗留时间也很短，基于以上分析，该系统可以考虑只开设1个服务台。

若系统中只有1个服务台时，即n=1，只考虑读者到馆多的情况，即λ1=50，计算结果如下：

(1)系统的流通强度ρ1=0.83，

(2)平均队长L3=5.329，

(3)逗留时间D3=0.10658，

(4)系统的损失率Ps3=0.278。

由以上计算结果可以看出，图书馆设置1个服务台，读者队列长度和逗留时间的增加值都很有限，也在读者接受范围之内，系统的流通强度也适中。

由以上结果对比可以看出，佳山校区图书馆服务台数量可以减少为1台。在实际操作中，1个服务台既承担借书服务，又可以承担还书服务，只需要服务人员切换一下汇文系统的操作页面即可。这样既可以让读者满意，也可以优化图书馆人力和物力资源。

四、结论

本模型以排队理论为基础，针对佳山校区图书馆的服务台设置问题，利用汇文系统的数据，经过统计分析和计算，针对读者的上课和下课两种时间段不同的到达率，分别给出系统的流通强度和读者的逗留时间，通过对比这些计算结果，在目前疫情防控要求下，可以假设佳山校区图书馆由原来的2个服务台数量减少到1台。当λ1=50，1个服务台的情况，计算出系统的流通强度和逗留时间。通过对计算结果进行对比，确定系统的服务台数量，以既可以达到读者的满意度，同时也可以减少图书馆管理费用。

本文中假设所有事件均服从负指数分布，下一步，可以针对汇文系统的数据进行数据回归分析。自疫情防控以来，图书馆线下借还书服务受到了很大的影响，同时图书馆线上服务资源的推广服务也在不断加强，读者不断体验到数字资源的获取更加快速和便捷，在未来很长一段时间内，读者线上阅览电子资源量将会呈上升趋势，所以后疫情时期，图书馆流通服务台数量的管理，也可以参照本文的结论。