建筑物多边形高精度识别的傅里叶形状描述子神经网络方法

刘鹏程，黄 欣，马宏然，杨 敏

1. 华中师范大学地理过程分析与模拟湖北省重点实验室，湖北 武汉 430079； 2. 华中师范大学城市与环境科学学院，湖北 武汉 430079； 3. 武汉大学资源与环境科学学院，湖北 武汉 430079

形状是物体最直观、有效且稳定的特征，是识别要素的重要途径，地图要素形状的描述和识别是地图空间认知的基本内容[1-2]，具有重要的应用价值。在地图综合领域，同一要素综合前后形状的相似性是评价综合算法优劣的一个重要指标。对建筑多边形形状的识别是近年来形状识别领域比较活跃的方向，相关应用包括建筑多边形的化简[3-6]、地图匹配[7]、变化检测等。建筑多边形作为人造要素，在地图中时常呈现出几种特定的模式，因而常常研究其与特定形状模板之间的匹配。文献[3]针对丹麦的农村房屋特点,利用一系列的英文字母模板来替代相似的建筑多边形并制作示意性地图。文献[4,6]给出了构建形状模版的原则并利用形状模板的精确匹配进行建筑多边形的化简。形状相似性判断是跨尺度建筑多边形的匹配依据之一，文献[7]基于形状相似性进行跨尺度多边形的匹配，从而进行不同尺度下建筑多边形的溯源。

形状相似性度量是建筑物多边形识别与匹配的重要依据，其计算主要包括两个步骤[8-9]：

(1) 提取建筑物的形状特征向量。圆形度、偏心率等形状特征向量作为单一数值的几何形状特征无法对形状进行准确表达[10]，而链码[11-12]、傅里叶形状描述子[1，13-16]、距离转角[17]、形状树[18]等形状特征以一维向量来描述二维形状，并能一定程度地还原形状，可以建立形状相似性的解析表达式，现已被广泛使用。

(2) 设计计算模型。形状特征向量的欧氏距离和夹角距离方法常被采用[19-20]。文献[16]采用傅里叶形状描述子的欧氏距离度量建筑多边形形状相似性，并比较了欧氏距离法和转角函数法的适宜对象。

人类对形状认知是大脑逻辑思维和形象思维的结合，任何模型的形状相似性的识别结果都需要通过人类的认知来检验。近年来兴起的深度学习方法结合了人类认知的非线性特点，已经逐步应用到地图要素形状识别领域。文献[7]通过图卷积神经网络对建筑多边形形状相似性进行了有效的尝试，该方法在节点数量归一化处理及节点属性计算过程的复杂度偏高。在形状识别的深度学习中，提取有效的形状特征向量是关键环节，特征向量既不能太复杂，又要辨识度高。傅里叶形状描述子满足上述两个条件，而且其向量长度与建筑多边形点数无关，还可以根据精度需要进行调节；傅里叶形状描述子通过傅里叶变换实现形模互转，已有成熟的数学模型。考虑到傅里叶形状描述子在识别形状时容易受到局部形状的扰动，因而将圆形度、偏心度和矩形度3个宏观形状特征参量补充到形状特征向量中，建立神经网络模型，在有监督的学习训练下建立建筑多边形与形状模板的匹配。试验证明该方法相比现有的形状识别方法具有较高识别精度，且模型的复杂度低。

1 形状特征向量提取

1.1 傅里叶形状描述子

建筑多边形是由一组首尾点重合的坐标串组成的闭合多边形。在平面直角坐标系中，在多边形的边界线上任取点P0(x0,y0)作为起点，再顺时针定义边界顶点P1、P2、…、PN，构成闭合建筑物边界轮廓(P0与PN重合)，如图1所示。

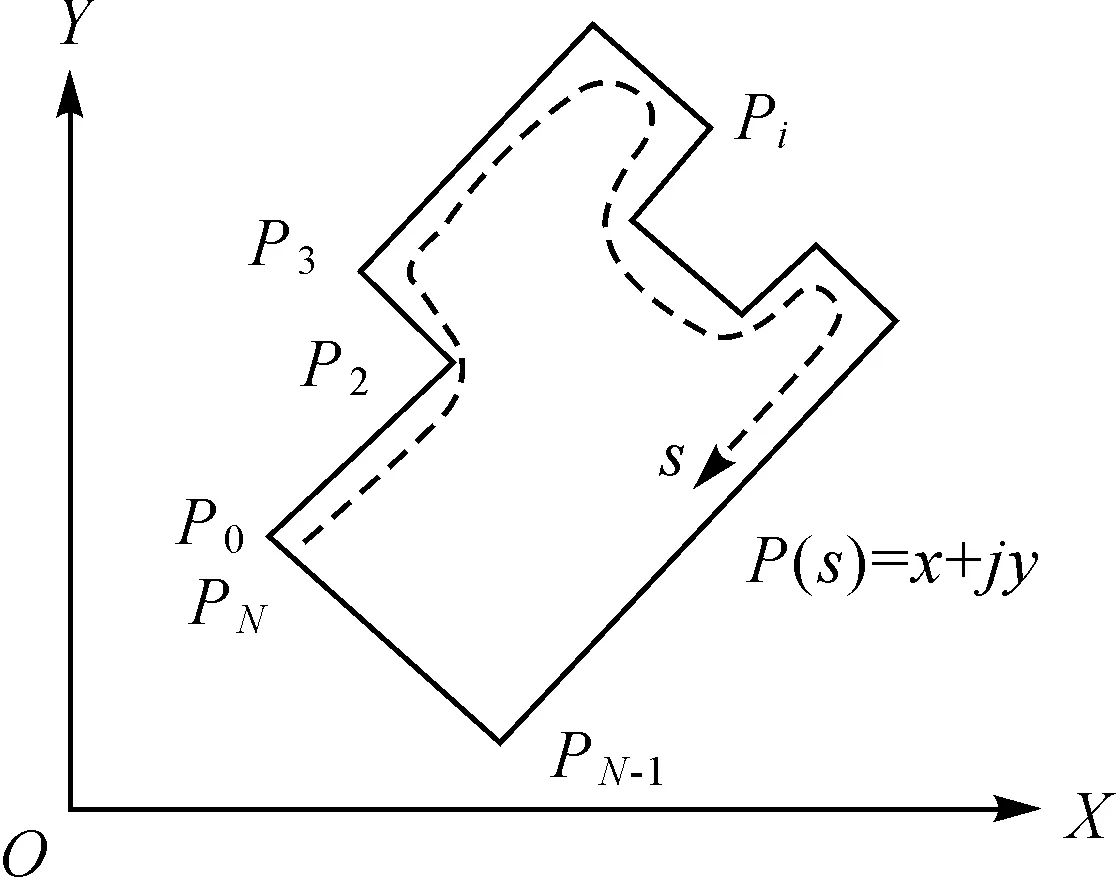
图1 多边形的分段复数函数表示Fig.1 Polygon shown as piecewise plural function

图1中边界上任意点P的坐标值(X(l),Y(l))均可表达为起点P0至P点的边界总长度l的分段函数[21]，具体表达式为

(1)

(2)

式中，(xi,yi)为边界顶点Pi的坐标；Li为起点P0到边界顶点Pi的线段长度和；Li≤l≤Li+1；0≤i≤N-1；N为建筑物边界顶点个数。

将平面坐标系中的要素引入复平面中，可以得到点P在复数域的坐标表达式为

P(l)=X(l)+j·Y(l)

(3)

式中，j为虚数单位，j2=-1。显然函数P(l)为以建筑物周长L为周期的周期函数[21]，故可以使用傅里叶级数来表示

(4)

各阶次傅里叶系数Fn的表达式为

(5)

傅里叶级数的各项系数Fn均为复数，取Fn的模向量构成傅里叶级数模向量F[22]，如式(6)

F=(‖F1‖,‖F2‖,…,‖Fn‖)

(6)

为了使傅里叶级数模向量F具有旋转、尺度和平移不变性，对其进行归一化处理，将模向量F中的每一项均除以第一项(系数F1的模)[22],考虑到处理后第一项的值均为1，则去除第1项后得到形状的傅里叶形状描述子，如式(7)所示

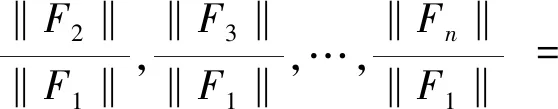
(d1,d2,…,dn-1)

(7)

式中，傅里叶形状描述子D的长度K趋于无限大，在形状识别中须根据实际精度截断[21]。

1.2 宏观形状特征参量

为降低局部形状扰动对傅里叶形状描述子在形状识别中的影响，将圆形度、偏心率和矩形度3个建筑多边形的宏观形状特征参量纳入形状识别的特征向量中，通过计算几何获取这些参数。

1.2.1 圆形度(circularity)

圆形度反映物体接近圆形的程度，是无量纲的形状特征描述，使用多边形的面积S和周长L计算得到

(8)

式中，C为圆形度，C∈(0,1]。在所有多边形中，圆的圆形度最大，值为1，正方形的圆形度为π/4。圆形度越接近于1，表明形状越接近于标准圆。

1.2.2 偏心率(eccentricity)

偏心率又称为伸长度，用来反映多边形形状相对圆形的扁平程度(图2)。偏心率有多种计算公式，本文采用多边形形状轮廓的最小外接矩形(MBR)的长度a和宽度b之比，计算公式为

图2 形状特征偏心率示意Fig.2 Eccentricity explanatory diagram of polygon

(9)

式中，E为偏心率，E∈[1,+∞)。在所有多边形中，圆和正方形的偏心率最小，值为1，形状越扁平值越大。

1.2.3 矩形度(rectangularity)

矩形度表示形状在其最小外接矩形中的填充程度,定义为物体的面积S0与物体最小外接矩形(MBR)的面积SR之比，计算如式(10)所示

(10)

式中，R为矩形度，R∈(0,1]，在所有多边形中，矩形的矩形度为1，圆形的矩形度为π/4，利用矩形度可以区分矩形、圆形和不规则形状。

2 建筑多边形形状识别神经网络的构建

2.1 特征向量长度设置

式(7)的傅里叶形状描述子是长度趋于无穷大的向量，其前面分量对应于低频信息，描述形状的轮廓信息，后面的分量对应于高频信息，描述形状的细节信息[23]。在形状度量中，可以根据实际精度需要保留傅里叶形状描述子前面一定长度的分量，舍弃后面的细节信息[24]。本文按照文献[16]的方法，通过傅里叶形状描述子还原的建筑多边形与原建筑物多边形的重叠度来确定傅里叶形状描述子的长度K。具体过程是：设原建筑多边形区域为MO，傅里叶形状描述子拟合区域为MF、MO和MF重叠区为Mo∩F，定义傅里叶形状描述子的近似度(A_degree)为式(11)

(11)

式中，S(Mo)、S(MF)、S(Mo∩F)分别对应MO、MF、Mo∩F的面积；A_degree∈(0,1]，其值越大傅里叶形状描述子的精度越高。随着K的增大，A_degree不断增大，拟合形状不断逼近原始要素。选择A_degree达到设定阈值(如0.98)所对应的傅里叶形状描述子为作为形状特征向量。图3是部分建筑多边形的傅里叶形状描述子的拟合试验，左边黑色的图形为原要素，蓝色部分为傅里叶形状描述子长度为K的拟合图形，红色为数字为傅里叶形状描述子的近似度，可以看出当K=50时，傅里叶形状描述子的近似度大于0.98，说明此时拟合的多边形形状已经按设定阈值还原了原要素。

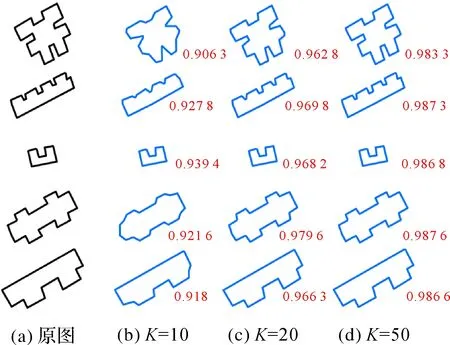
图3 傅里叶形状描述子的长度与近似精度的关系Fig.3 The approximation of Fourier descriptors with different lengths

本文所设计的神经网络输入的特征向量包含了长度为50的傅里叶形状描述子及3个宏观形状特征参量，如图4所示。

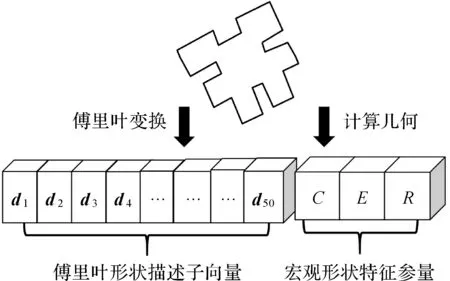
图4 神经网络的输入向量Fig.4 The input characteristic vector of neural network

2.2 形状识别神经网络的设计

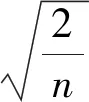
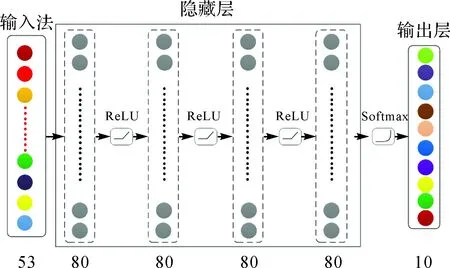
图5 神经网络形状识别模型结构Fig.5 The architecture of neural network for shape recognition

3 建筑多边形的形状识别试验及实践应用

3.1 形状识别试验及方法对比

本文使用文献[25]提供的已知正确标签值的5000个建筑物多边形数据作为试验数据，对数据进行旋转、镜像等操作，生成6250个多边形样本数据。从样本数据中提取10个稳定的且频繁重复出现的建筑物形状，进行边界简化作为建筑物模板，构建建筑物形状模板库。模板的构建遵循抽象性、正交性、代表典型性、简单清晰等原则，且综合考虑了建筑物模板形状特征要具备易区分性，最终确定了10个建筑物形状模板，形如英文字母L、Z、O、Y、T、E、U、F，属于常见的中国城市建筑物形状类型，大部分具有直角转角和对称的特点。建筑物模板的名称及其对应的形状具体见表1。

表1 10种类型的建筑物形状模板Tab.1 10 types of building polygon shape temples

在具体的试验操作中，将6250个多边形样本按照8∶2的比例将其划分为训练数据集和测试数据集，即随机抽取5000个作为训练样本，剩余1250个为测试集。图6为神经网络模型在训练和测试过程中精度的动态变化。由图6可知，当训练的历元到达2000时，训练精度和测试精度分别为98.7%、96.4%。为了验证3个宏观形状特征参量值在识别中作用，只用单一的傅里叶形状描述子(长度为50)作为神经网络的输入向量进行训练，发现其拟合精度和测试精度下降到86.5%和83.6%，说明3个宏观形状特征参量值可以提高神经网络的精度。

图6 神经网络的训练精度和测试精度Fig.6 The accuracy-epoch curves of neural network

同时将1000个测试样本采用欧氏距离法和转角函数法进行了形状识别对比研究，表2为试验中部分结果数据。表2中每个测试数据均采用3种方法与建筑物形状模板进行匹配，其中第1行对应傅里叶形状描述子的欧氏距离(ED)的结果，每列分别是与各形状模板的傅里叶形状描述子间的欧氏距离，最小距离(加粗)对应匹配的模板。第2行对应转角函数法(TA),计算测试样本与每个模板的转角函数值，最小值(加粗)对应匹配模板。第3行是本文的神经网络方法(NN)，每列为测试样本匹配为各个模板的概率值，最大(加粗)为匹配结果。表2的最后1列为识别正确性判断。

表2 使用不同形状识别方法的建筑多边形与形状模板的匹配Tab.2 The match of shape between the template and candidate buildings by different shape recognition methods

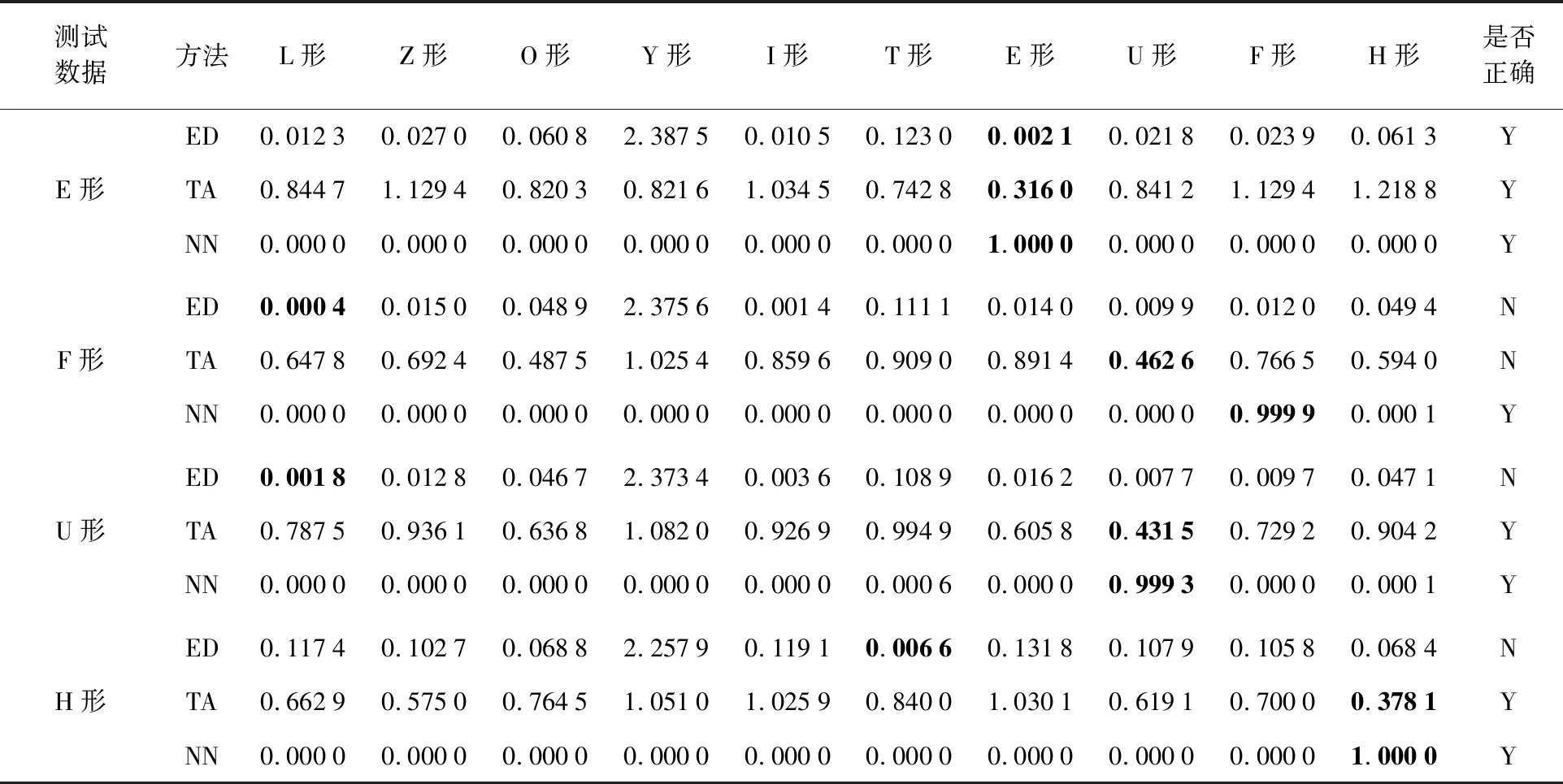
续表2

表3统计了试验中3种方法的测试精度，其中，本文神经网络方法的形状识别精度高达98.7%，转角函数法的精度为79.5%，而傅里叶形状描述子的欧氏距离法只能达到17.2%。从结果来看，形状局部扰动直接影响傅里叶形状描述子的欧氏距离判断精度，而以傅里叶形状描述子和宏观形状特征参量为输入值的神经网络精度最好。

表3 不同形状识别方法精度表Tab.3 Precision table of different shape recognition methods

3.2 模型的实践应用

为证明本文方法在形状识别上的普适性和可行性，在OpenStreetMap网站(https:∥www.openstreetmap.org/)下载武汉市、郑州市两个城市的建筑物矢量数据，利用训练好的神经网络对城市各个建筑物进行多边形识别，表4为两个城市建筑物多边形的分类结果，图7给出了部分识别结果的示意图。从识别结果来看，基本与人的认知相符，有少部分O形被错误识别为I形，但对于这部分多边形，人也无法准确地进行类别的划分。有些边界复杂的多边形被识别为F形，针对该问题需要后期补充形状模板的类型。

图7 武汉和郑州建筑多边形形状识别结果局部Fig.7 The local graph of the building-polygons shape recognition results of Wuhan and Zhengzhou

表4 武汉市和郑州市建筑多边形的各类型数量、占比Tab.4 The amount, ratio of different types building-polygon and information entropy in Wuhan and Zhengzhou

4 总结与讨论

将神经网络方法应用于建筑多边形的形状识别是一种有效结合人的认知试验、数学模型、计算机拟合的方法，其中样本标签属于认知试验，形状特征提取属于数学模型，而神经网络训练中的参数调整属于计算机的逼近和拟合。本文提取傅里叶形状描述子、圆形度、偏心率和矩形度作为神经网络的输入特征向量，构建了建筑多边形形状识别的神经网络方法，试验证明该方法比经典的傅里叶形状描述子欧氏距离法、转角函数法识别精度高。本文所选用的形状特征向量中，傅里叶形状描述子有经典的提取模型，能够将二维延展的要素形状转化为一维的傅里叶级数模向量，可以根据拟合精度的要求控制模向量的长度，不需要通过建筑多边形的节点加密来保证不同多边形的模向量长度，且傅里叶形状描述子能基本还原建筑多边形的形状，说明其形状描述上具有科学性。另外，由于傅里叶形状描述子是多边形频谱的能量反映，多边形中任何微小的变化都将会引起所有频率的幅值变化，这样容易造成傅里叶形状描述子在形状识别中不稳定，本文将圆形度、偏心率和矩形度等宏观形状特征参量纳入形状特征向量，起到抑制作用。后续工作中，笔者将本文方法实际应用到城市建筑物形状识别工作中，将进一步地探索其他要素(如自然要素)的形状识别问题。