顾及局部差异的航海图线要素复杂度度量
魏泓丞,张立华,唐露露,董 箭,李改肖,袁 浩
海军大连舰艇学院军事海洋与测绘系,辽宁 大连 116018
航海图线要素综合作为海图制图综合中的重要内容,其自动综合的研究始终受到人们的关注[1]。针对航海图上线要素的自动综合,国内外众多专家学者提出了不少算法[2-7],这些算法多采用固定阈值或同一尺度对图上要素进行综合。然而,在经典著作[1]、法律规范[8]及相关研究[9-11]的描述中,均强调在制图综合过程中需要依据图上情形适当调整综合尺度,即在复杂区域,综合尺度可适当减小;在简单区域,综合尺度可适当增大。由于这一描述较为模糊,且对于图上线要素而言,其复杂程度常常难以界定,从而使得当前的综合尺度无法随着图上局部区域复杂程度的不同而变化,进而使得自动综合的研究陷入瓶颈。
为了解决上述问题,众多专家学者针对线要素的复杂程度定量化评估提出了不少模型算法[11-20]。文献[11]依据边的振动频率及幅度,从凹口比例、凸壳周长相对增量及最小外包圆面积相对增量3个方面建立复杂性度量模型。文献[12—16]基于分形理论,利用分形维数描述曲线的复杂程度。文献[17—18]通过傅里叶变换将地理线要素从空间域转化到频率域进行分析,从频率的角度分析并定义了线要素的复杂程度。文献[19—20]主要基于几何分析,通过线要素的几何形状、几何拓扑、几何分布来描述线要素的复杂程度。上述这些模型都是针对单一线或面状要素,通过计算曲线自身特征(分维数、频率、振动频率)获取曲线的复杂程度,取得了较好的试验效果。然而,在实际航海图上,曲线的复杂程度不仅需要顾及自身基本特性,还应当考虑曲线周围的其他线要素,即使对于单一线要素而言,其不同部分的复杂程度也是不尽相同的。如图1(a)所示,曲线部分A(图1(a)红色矩形所围部分)与部分B(图1(a)蓝色矩形所围部分)相比,显然A要比B复杂得多。类似地,对于多条线要素而言,其图上不同区域的复杂程度也是不尽相同,如图1(b)中的区域C(图1(b)红色矩形所围部分)与区域D(图1(b)蓝色矩形所围部分),显然,区域C比区域D要复杂得多。若直接采用上述方法评估图1所示曲线复杂程度,则只能得到各单一曲线的整体复杂程度,不能准确表示出图上线要素在各区域的差异性,难以实现图上线要素复杂程度的精细化度量。

图1 不同分布线要素复杂程度对比Fig.1 Comparison of complexity between line elements with different distribution
考虑到当前线要素复杂度的度量方法多基于单一线要素求取整体复杂程度,未顾及线要素在各区域的差异性,本文提出一种顾及局部差异的航海图线要素复杂度度量方法。在分析线要素复杂区域与简单区域特点的基础上,通过构建约束Delaunay三角网、计算线要素数据点复杂度及内插等步骤,实现了图上线要素复杂程度的精细化评估。
1 顾及局部差异的线要素复杂度模型
1.1 基本思想
区分图1所示区域中各线要素复杂区域(区域A和区域C)与简单区域(区域B与区域D)的关键点在于采用某种模型或方法对其进行定量化描述。而Delaunay三角网作为空间分析的重要工具,被大量应用于空间邻近关系探测、弯曲识别、冲突关系探测等[21-24],并取得了较好的探测效果。因此,为探索关于线要素复杂度的评估模型,本文针对单一线要素及多条线要素分别构建约束Delaunay三角网,如图2所示。

图2 不同线要素约束Delaunay三角网构建Fig.2 The construction of constrained Delaunay triangulation with different line elements
由图2可知,曲线L1及线要素L2、L3构成区域与图1中的线要素相类似,其左侧区域(红色矩形所示区域)明显比右侧区域(蓝色矩形所示区域)复杂。在构建约束三角网以后,分别从复杂区域(红色矩形所示区域)以及简单区域(蓝色矩形所示区域)任取三角形T1、T3(图2中蓝色三角形所示)、T2、T4(图2中绿色三角形所示),不难看出,无论线要素数量多少,其复杂区域三角形T1、T3的边长明显要比简单区域三角形T2、T4的边长要短很多,且对于区域内的其他三角形,也具有相同的特性。基于此,不难得出结论:无论线要素数量多少,在构建约束Delaunay三角网后,线要素越复杂,其三角形边长越短;反之,线要素越简单,则三角形边长越长。
基于上述分析,线要素的复杂程度可采用Delaunay三角网中三角形边长近似反映。为此,本文使用Delaunay三角网中三角形边的长度变化对线要素复杂程度进行定量化描述,流程如图3所示。

图3 本文方法主要流程Fig.3 The main process of proposed method
1.2 约束Delaunay三角网构建
在航海图上,线要素分布常常复杂多样,且曲线上数据点的疏密程度也分布各异。考虑到本文主要尝试使用三角形的边反映曲线的距离变化,因此采用约束Delaunay三角网作为本文的基础算法。所谓约束Delaunay三角网实际上是指在构建三角网时,强行使曲线上的线段成为三角形的一条边,避免三角形的边与直线段相交,从而得到约束Delaunay三角网[25](图4)。对图4(a)的曲线要素构建约束Delaunay三角网如图4(b)所示,任取其中一个三角形T1(图4(b)中蓝色三角形所示),边BC为原始曲线L3上的线段,将这种三角形中为原始曲线线段的边称之为约束边,同理将其中不为原始曲线线段的边(如图4(b)中的线段AB、AC)称之为非约束边[25]。

图4 约束Delaunay三角网构建Fig.4 The construction of constrained Delaunay triangulation
同时,考虑到曲线上数据点疏密分布不均,若直接构建三角网会出现众多狭长三角形进而影响计算结果,为此对曲线上数据点进行加密[24],其加密后的约束三角网如图4(c)所示。比对图4(b)与图4(c)不难看出,经数据点加密后的约束三角网,三角形更为密集,更能反映曲线间距离变化。
1.3 曲线数据点复杂度计算
1.3.1 数据点复杂度定义
依据1.1节的相关描述,利用约束三角网可对线要素间距离变化进行探测,进而反映出曲线复杂程度的变化。然而,这一描述仍然是定性的描述,无法直接计算曲线复杂程度,因此,如何建立三角形边长与曲线复杂程度之间的定量映射关系就成了亟须解决的问题。为此,本文尝试采用曲线上数据点的复杂程度描述曲线在该数据点附近的复杂程度(图5),并将曲线上数据点复杂度定义为与该数据点相关非约束边平均长度的倒数,其计算公式为
(1)
式中,di表示各非约束边的长度;n表示非约束边的数量值。
对图5(a)所示线要素构建约束Delaunay三角网如图5(b)所示,任取其中一个数据点A,依据构建的三角网可知,与点A相关的边有AB、AC、AD、AE、AF、AG,其中边AB与AD为原始曲线L2上的线段(即约束边),其他边均为非约束边。依据1.2节的相关描述可知,在约束Delaunay三角网构建时,需对曲线上的数据点进行加密处理,因此,上述约束边的长度常被人为给定,且约束边的长度实质上反映的是曲线上数据点的疏密变化,与本文需反映的线要素间的距离变化并无直接关联,因此在计算数据点复杂度时应当予以剔除。即计算图5(b)中点A处的复杂度时,应当剔除边AB与AD,仅考虑边AC、AE、AF、AG,并使用式(1)计算其复杂程度。

图5 数据点复杂度定义Fig.5 The definition of data point complexity
1.3.2 异常边剔除
在实际航海图上,线要素分布繁杂多样,其构建形成的约束Delaunay三角网也种类繁多。在计算数据点复杂度时还存在一类情形,如图6所示,对曲线L1与L2构建约束三角网后,其中曲线L2上与数据点A相关的非约束边有AB、AC、AD、AE、AF、AG,其中边AF、AG长度明显大于其他非约束边,若不加处理直接计算点A复杂度,将导致点A复杂度偏小,进而使得计算结果无法正确反映实际复杂程度。因此,有必要对该类型非约束边进行剔除。本文将这种长度明显长于其他非约束边,且明显影响复杂度计算的非约束边称之为异常边。
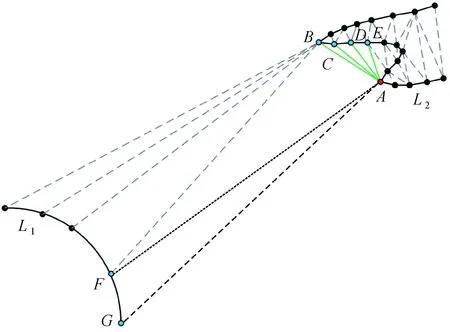
图6 异常边剔除Fig.6 The rejection of abnormal edges
基于上述分析,为保证复杂度值计算的合理性与准确性,本文采用拉依达准则(3σ准则)对异常边进行识别并剔除。其具体过程如下:
(1) 依据构建的三角网,获取与数据点相关的所有非约束边的长度值,记为d1、d2、…、dn。如图6中与点A相关的非约束边AB、AC、AD、AE、AF、AG的长度值,可分别记为d1、d2、…、d6。
(2) 依据步骤(1)中的长度值,按照式(2)计算标准差σ

(2)

(3) 针对步骤(1)中的全体非约束边长度值,依据式(3)做如下判断:若某条非约束边的长度d满足

(3)
则认为该非约束边的长度是含有粗大误差值的异常值(n的取值可为1、2、3),该非约束边为异常边。
需要说明的是,式(3)中的n值可取1、2、3,但经笔者多次试验,发现当该值取2时,其识别效果最优,可识别绝大部分的异常边,因此本文建议将该值取为2。
1.4 航海图线要素复杂场计算
通过1.3节的相关步骤,可计算出曲线上各数据点所在位置的复杂程度,然而,其结果为相对离散点的复杂度,仍无法反映整张航海图线要素的复杂程度变化。因此,本文采用空间插值的方法对上述离散复杂度进行内插,从而得到了连续的线要素复杂场,实现了航海图线要素复杂度评估由离散线到面的跃升。
当前空间插值算法相对较多,主要有泰森(Thiessen)多边形法、反距离加权法、样条函数法、克立格(Kriging)插值法、线性内插法、双线性多项式插值法、自然邻点插值法、趋势面法等[26-27],经过多次试验,自然邻点插值法[28-32]效果最优,因此本文采用自然邻点插值法对离散点复杂度进行内插。复杂场求取主要步骤如下:
(1) 输入航海图线要素数据,构建约束Delaunay三角网。
(2) 逐一遍历线要素上的数据点,并依据1.3节所述方法计算各数据点复杂程度。
(3) 采用自然邻点插值法对上述各数据点的复杂度进行内插,即得到航海图线要素复杂场,并输出结果。
如图7所示,对图7(a)所示的线要素采用本文方法计算各点复杂度如图7(b)所示,随后采用自然邻点插值法对其进行内插,并根据复杂度的大小对试验结果显示成图,如图7(c)所示。

图7 复杂场求取Fig.7 The calculation of complex field
2 试验与分析
2.1 线要素复杂度有效性试验
为对本文方法的有效性进行验证,本文分别选取了3组单一线要素和多线要素作为试验对象。运用本文复杂性度量方法,按照1.4节的步骤分别计算出线要素上各点的复杂度,经过自然邻点法内插生成复杂场,利用C++及动态库GDAL2.2.0编程实现,并使用ArcGIS对试验结果进行显示成图。
2.1.1 单一线要素
为了验证本文方法对线要素各区域复杂程度的识别效果,首先选取了3组不同形状的单一线要素作为试验对象,如图8所示,其中图8(a)、(c)、(e)为原始线要素,图8(b)、(d)、(f)为本文方法生成的相对应的复杂场。由图8(a)、(c)、(e)可以看出每个区域的复杂程度是明显不同的,同时各复杂区域的分布也是不同的,可较好地验证本文方法的有效性。在图8(b)、(d)、(f)中为了方便对各复杂区域进行区分,根据复杂度的数值采用热力图对计算结果进行显示成图。

图8 单一线要素复杂场Fig.8 The complex field of single line element
在图8(a)、(c)、(e)原始线要素中,线要素越曲折、震荡越剧烈的区域,在图8(b)、(d)、(f)对应复杂场中表示的颜色就越鲜艳,其对应复杂度的值也就越大;在图8(a)、(c)、(e)原始线要素中,线要素越平缓、震荡越轻微的区域,在图8(b)、(d)、(f)对应复杂场中表示的颜色就越蓝,其对应复杂度的值也就越小。
2.1.2 多条线要素
上述试验验证了本文方法针对单一线要素具有较好的识别效果。为了进一步检验本文方法的有效性及适用性,又另选取3组分布各异的多条线要素作为试验对象。如图9所示,图9(a)、(c)、(e)为原始线要素,图9(b)、(d)、(f)为本文方法生成的复杂场。从图9(a)、(c)、(e)中可以看出,同一线要素上各区域的复杂程度是明显不同的,同时线与线之间的紧密程度也是不同的,且分布各异,因此可较好地验证复杂度评估模型的有效性。

图9 多线要素复杂场Fig.9 The complex field of multiline elements
由图9可知,在图9(a)、(c)、(e)原始线要素中,线要素越曲折,线与线之间越紧密的区域,在图9(b)、(d)、(f)对应复杂场中表示的颜色越鲜艳,其对应复杂度的值也就越大;在图9(a)、(c)、(e)原始线要素中,线要素越平缓,线与线之间越稀疏的区域,在图9(b)、(d)、(f)对应复杂场中表示的颜色就越蓝,其对应复杂度的值也就越小。由试验结果来看,线要素简单稀疏的区域和复杂紧密的区域均被较好地识别区分出来,且对各区域的复杂程度进行了较好的度量。
综合来看,对于上述单线要素以及多线要素,运用本文方法可较好地区分复杂与简单区域,且能够定量评估线要素在各区域的复杂度。
2.2 航海图线要素复杂度统计分析试验
为对本文复杂度模型的有效性及适用性进行整体性验证,选取了两组分布各异的航海图作为试验数据,利用ArcGIS对试验结果进行显示成图,同时为了评估本文方法对线要素复杂程度的识别情况,采用问卷调查、统计分析的方法,对线要素复杂度场模型的识别效果进行评估分析。受调查者中,主要分为3类人群,普通人群(50人)、具有一定测绘专业基础知识的人群(35人)、专家学者(10人),由这95人对线要素复杂度模型的识别结果进行评判。
2.2.1 试验区域1(C13640)
本次试验海区数据选自由中国航海图书出版社发行的普通航海图C13640,图10(a)为经测试者划分的复杂区域,图10(b)为由线要素复杂度场模型划分的复杂区域(采用热力图的方式表示复杂度不同的各区域),并将关于复杂区域识别效果的问卷调查统计结果展示如图11所示。

图10 线要素复杂场Fig.10 The complex field of line elements

图11 识别效果统计Fig.11 The statistical of recognition result
由图10可以看出,由本文方法划分的复杂区域与测试者划分的复杂区域基本一致,其中5、6、7、9这4块区域识别效果最好,能较好地区分出复杂程度不同的各线要素区域。同时由图11问卷调查的统计结果可知,在普通人群中,超过九成以上的受访者认为本文方法对复杂区域的识别效果较好,其中8人认为识别结果完全一致。在有测绘专业基础的人群中,94%的受访者认为本文方法对复杂区域的识别效果为基本一致及以上,其中10人认为识别结果完全一致。在对专家学者的识别度调查中,普遍认为场模型对复杂区域的识别划分效果较好。
2.2.2 试验区域2(C12351)
为了进一步评判线要素复杂度场模型对复杂区域的识别效果,本文选取了另一幅航海图作为试验数据,该图选自中国航海图书出版社发行的大比例尺港湾图C12351,图12(a)为经测试者划分的复杂区域,图12(b)为由本文方法划分的复杂区域,并将识别效果的问卷调查统计结果展示如图13所示。
由图12可以看出,相对上一组试验本海区线要素要更为复杂,但由本文方法划分的复杂区域与测试者划分的复杂区域基本一致,其中1、2、3、4、5这5块区域识别效果比较好。同时,由图13可知,在普通人群中,94%的受访者认为本文所提的线要素复杂度场模型对复杂区域的识别效果较好,其中35人认为基本一致,12人认为完全一致。在有测绘专业基础的人群中,九成以上的受访者也认为本文所提方法对复杂区域的识别划分效果较好。在对专家学者的识别度调查中,8人认为基本一致,2人认为完全一致,均认为本文算法识别效果较好。
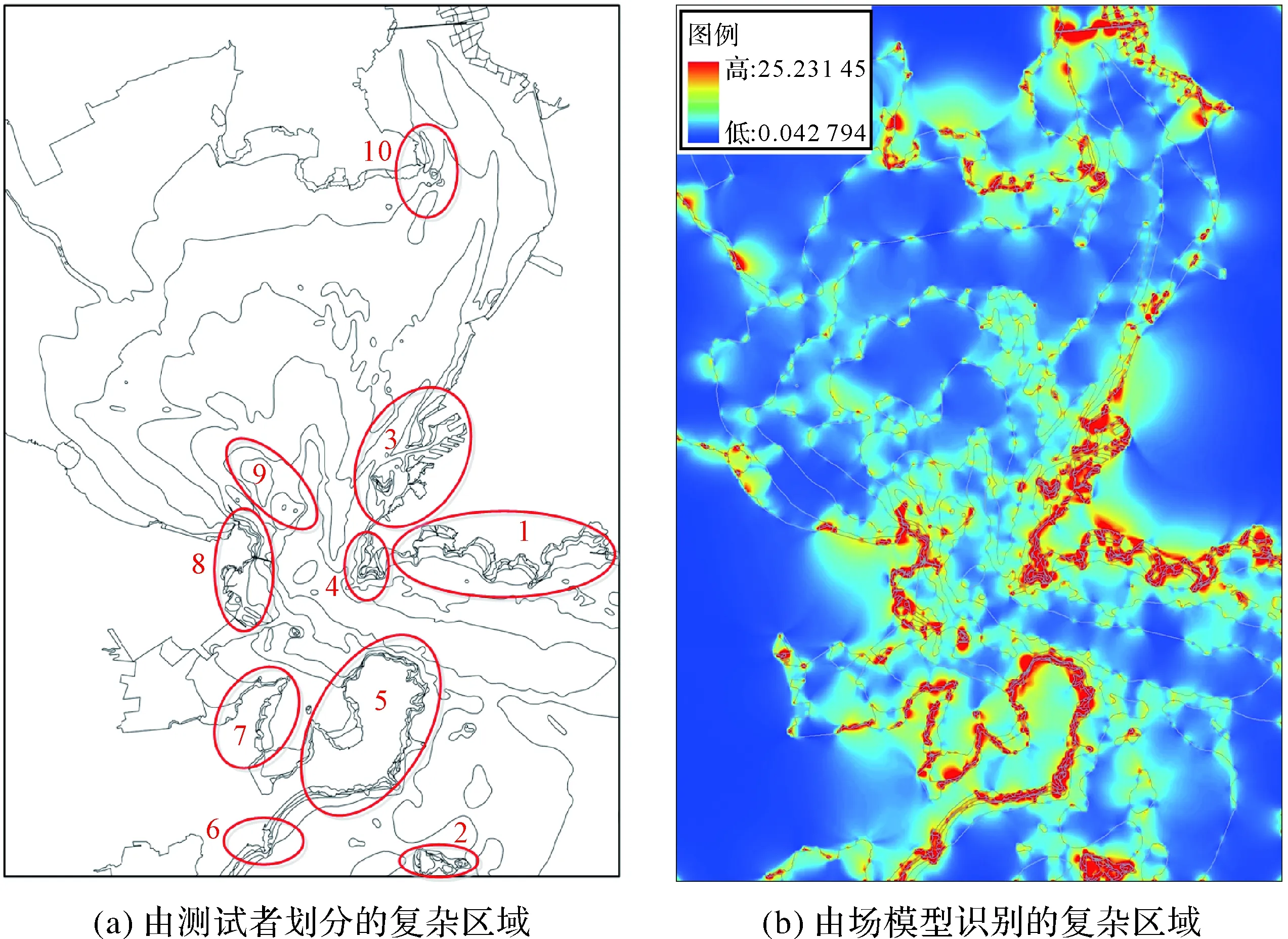
图12 线要素复杂场Fig.12 The complex field of line elements
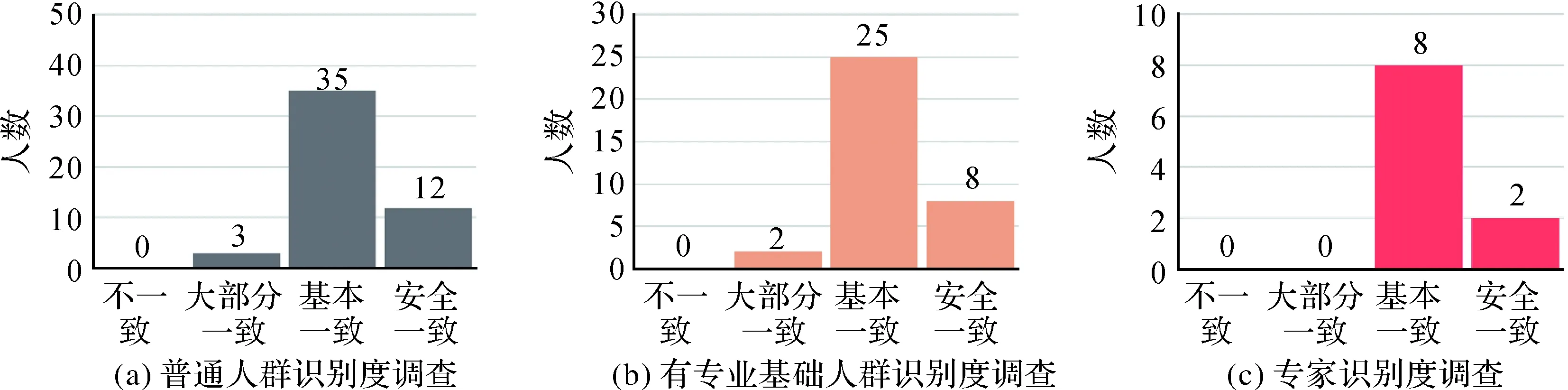
图13 识别效果统计Fig.13 The statistic of recognition result
2.2.3 总体评估试验
为了进一步说明本文所提方法对复杂区域的识别划分能力,对受访者做了一个关于两幅图总体识别效果的问卷调查,具体统计结果如图14所示。

图14 总体识别效果统计Fig14 The statistic of holistic recognition result
本文方法对于所选取的两组分布各异的航海图区域,总体识别效果良好。由图14可知,在普通人群与有测绘专业基础的人群中,超过九成的受访者认为本文方法对复杂区域的总体识别效果表示认可,在对专家学者的识别度调查中,均认为线要素复杂度场模型对复杂区域的总体识别效果较好,统计结果都为基本一致。
综上所述,从试验结果及问卷调查的统计结果来看,本文方法取得了较好的识别效果,未出现明显识别错误的区域,很好地符合了人们对线要素复杂程度的视觉感受,能较好地定量评估出不同线要素区域的复杂程度。
3 结 论
本文提出了一种顾及局部差异的航海图线要素复杂度度量方法。该方法从线要素节点所构三角网边长与线要素复杂程度的关联性出发,通过构建约束Delaunay三角网、计算数据点复杂度以及内插等步骤,最终得到了航海图线要素复杂度场模型,经理论推导及试验比对分析,得出结论如下:本文方法顾及了线要素在图上各区域的差异性,将线要素复杂度的计算,由对离散线的度量上升到对整个面的度量,能较好地定义航海图线要素的复杂度,可精细化地定量评估航海图线要素在各区域的复杂程度。

