基于反向策略的混沌麻雀搜索算法
钱 敏,黄海松,范青松
(贵州大学现代制造技术教育部重点实验室,贵州 贵阳 550025)
1 引言
近期,群体智能(Swarm Intelligence,SI)优化算法备受学者的关注,如Kennedy等人[1]模拟自然界中鸟群捕食行为,研究种群觅食的搜索机制从而提出了一种全局寻优的粒子群优化算法(Particle Swarm Optimization,PSO);Suash Deb等人[2]模拟布谷鸟独特的寄生行为,运用与其它鸟类相似的飞行搜索策略,从而提出了一种布谷鸟搜索算法(Cuckoo Search Via Lévy Flights,CS);Seyedali Mirjalili等人[3]模拟狼群中的头狼引导群体捕食的社会行为进行数学建模,从而提出了一种灰狼算法(Grey Wolf Optimizer,GWO)。此外,根据鲸鱼自身的泡泡网觅食方法进行食物的搜索,与改进螺旋方式进行位置的更新,而提出了一种鲸鱼优化算法[4](Whale Optimization Algorithm,WOA)。由于SI算法参数仅存在少数需要调整、易于实现且操作难度低,所以在各个领域应用广泛[5-8]。
无免费午餐定理(No Free Lunch,NFL)[9]表明任何一种算法只能解决一部分问题而不能优化工程实际中存在的所有问题,因而不断有学者提出改进的SI算法。如刘雪红等人[10]提出一种可行领域结构与精英分批两种策略对候鸟算法进行改进,有效提高了算法全局搜索效率(Improved Migrating Birds Optimization,IMBO):张文胜等人[11]提出一种自适应递减的收敛因子,并在灰狼位置更新公式引入惯性权重从而协调算法的全局领导与开发能力(Transformed Grey Wolf Optimizer Algorithm,TGWO);王乐洋等人[12]通过采用分段惯性因子调整粒子速度,修改局部和全局最优解的加速因子从而降低算法后期陷入局部最优的风险(Dynamic Particle Swarm Optimization,DPSO);吴泽忠等人[13]在初始化种群时采用反向学习策略及随机调整控制参数策略,利用正态变异算子与改进螺旋更新位置对鲸鱼种群进行干扰从而提高全局搜索速度(Improved The Whale Optimization Algorithm,IMWOA)。麻雀搜索算法(Sparrow Search Algorithm,SSA)是由Jiankai Xue等人[14]于2020年提出的一种新型SI优化算法。该算法模拟麻雀的觅食和反捕食行为,具体为一类麻雀领导觅食,另一类麻雀跟随并抢夺食物等过程找寻全局最优食物来源等一系列的捕食行为。与其它现有算法相比,SSA求解精度、收敛速度、稳定性和鲁棒性均有较好的性能,但仍无法避免种群寻优前期多样性较差导致搜寻速度较慢,降低了整体搜索速度,后期也存在陷入局部最优的风险。
本文针对SSA种群初始质量较差与后期易陷入局部最优的缺陷提出了新的改进方案,在SSA搜索前期,利用反向学习策略丰富种群多样性加快全局收敛速度,后期引入混沌策略进行干扰以降低陷入局部最优的风险。通过与其余四种SI算法相比,ISSA在求解12个基本测试函数函数上寻优性能更好,且能够有效提高算法的收敛精度及稳定性。
2 麻雀搜索算法
SSA是模拟自然界中麻雀觅食和抢食行为的一种新型SI优化算法。SSA将麻雀种群分为领导者与跟随者两类,种群中的领导者积极寻找食物来源,跟随者则由领导者引导觅食从而获取食物。为更快地获取食物,跟随者会不停地监视领导者的行为,若发现比自身更好的食物来源时,便上前进行抢夺。成功掠食则意味跟随者拥有了更好的食物来源,麻雀的身份便由跟随者转换为领导者,发现危险时引导麻雀逃离[14]。种群中领导者位置更新的数学模型如下
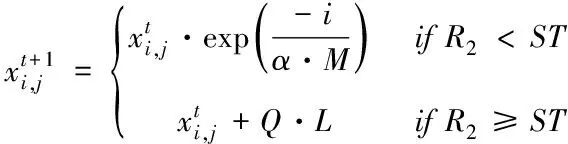
(1)
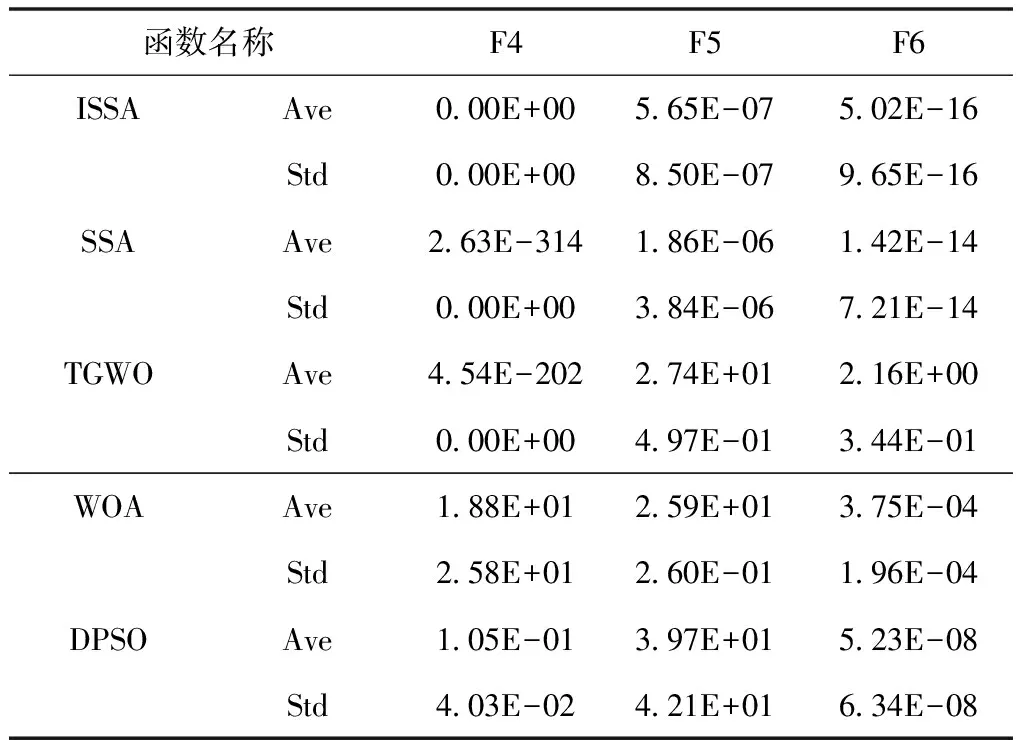
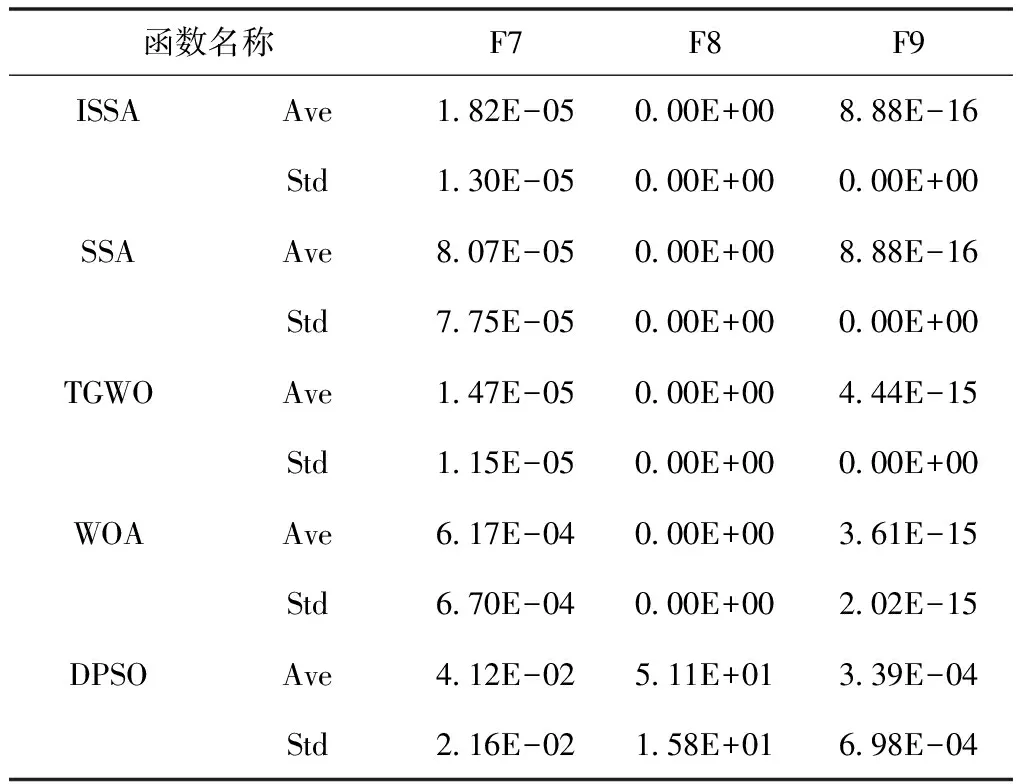
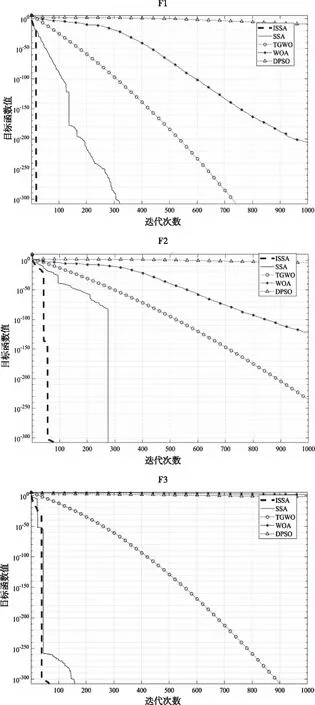
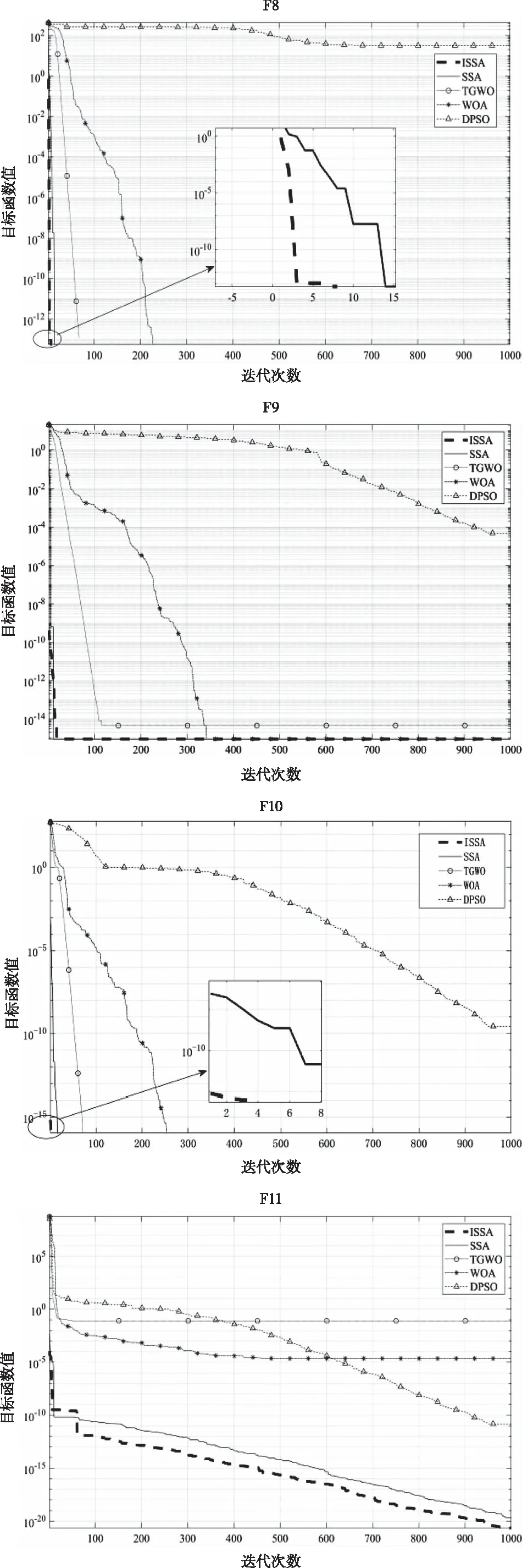
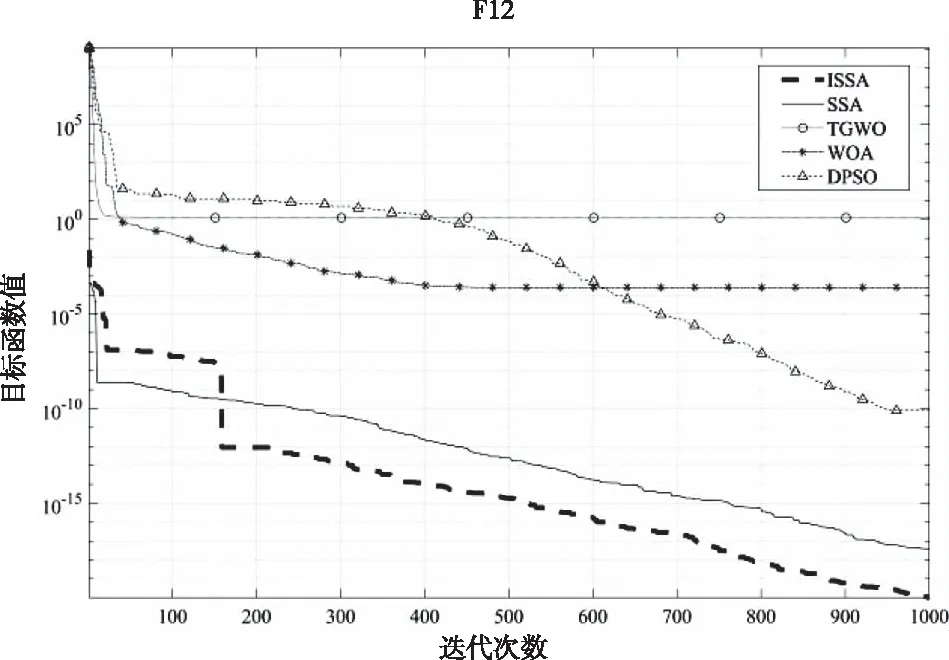
其中,第i只麻雀在第d维空间上的位置由xi,d表示。j=1,2,…,d,t是当前迭代次数。M是最大迭代次数,α∈(0,1]是随机数,R2∈(0,1]和ST∈(0.5,1.0]分别表示警报值和安全阀值。Q是服从均值为0标准差为1的高斯分布的随机数,L是每个元素都为1的1×d矩阵。当R2 种群里的追随者在觅食的同时会监视领导者,一旦发现位置更好的领导者便立即前往进行抢夺。若抢夺失败,则继续跟随觅食;其位置更新如下 (2) 意识到危险的麻雀占种群数量的20%,其位置更新如下 (3) SSA算法流程见图1。 图1 SSA算法流程图 反向学习策略 (Opposition-based Learning,OBL)由Tizhoosh 等人[15]引入,此策略被学者广泛应用于SI算法,并取得了较好的实验效果[16-19]。SSA在寻优前期采用随机初始化种群,导致搜索初期种群的多样性较差从而影响全局搜索的效率。种群初始化的质量好坏是影响全局寻优快慢的重要因素,因此本文在麻雀种群初始位置引入反向学习策略,扩大麻雀的搜索空间提高种群初期质量以增强全局搜索能力。反向学习策略通过选择原始种群和对立种群的最优解形成新的麻雀种群,其伪代码如下。 Algorithm 1 initiation based on opposition-based learning Set population size n,Search range boundary maximumμ,boundary minimum l,opposite solution oxi,j fori=1to n do for j=1to n do xi,j=li,j+rand(0,1)·(μi,j-li,j) end for end for for i=1 to n do for j=1 to n do oxi,j=li,j+μi,j-xi,j end for end for {x(n)∪ox(n)},Choose a better population 混沌系统具有随机性、遍历性,因此将混沌理论与SI算法结合是改进优化算法的一种思路,研究表明其能有效逃离局部最优和提高收敛精度[20-23]。SSA在寻找最优解时可能会陷入局部最优,其会导致寻优精度与收敛速度的降低。因此,本文在麻雀搜索后期引入Sinusoidal map混沌映射[24],避免麻雀种群在搜索过程中陷入局部最优。Sinusoidal map映射的数学表达式如下 (4) 麻雀经过扰动后的位置如下 xSi=g(i)·xi (5) 通过对比扰动前后种群中麻雀的位置,保留适应度值较优的麻雀。其中g(1)=0.7,a=2.3。 ISSA算法流程图见图2,详细步骤如下: Step1:设置麻雀算法初始参数,麻雀种群数量n,当前迭代次数t,领导者数量PD,跟随者数量SD,最大迭代次数G。 Step2:随机生成麻雀个体位置,再引入反向策略得到麻雀对立位置。 Step3:计算麻雀种群适应度值并进行排序,得到xp及xworst。 Step4:根据等式(1)更新种群中的领导者位置。R2 Step5:根据等式(2)更新跟随者位置,跟随者觅食同时会监视领导者并抢夺食物。 Step6:根据等式(3)更新意识到危险的麻雀位置。 Step8:重复Step4至Step7,直至满足寻优要求结束。 图2 ISSA算法流程图 为验证改进麻雀算法的寻优能力,本文将它用于求解12个国际上通用的标准测试函数,并与SSA、TGWO、WOA与DPSO进行实验比较。测试函数见表1所示,其中F1-F7是单峰测试基准函数,F8-F12是多峰测试基准函数其测试函数具体表达式及变量范围。单峰函数用来衡量算法的局部开发能力,多峰函数衡量全局搜索与局部开发的平衡性能。 表1 标准测试函数(维度=30) 本文算法参数设置为:迭代次数为1000,种群数量为100。TGWO算法中,φmax=0.9,φmin=0.4;WOA算法参数a在整个搜索中由2下降为0;DPSO中C1s=C2e=1,C1e=C2s=2.05。本文实验中ISSA与其余四种算法各运行30次,分别计算Ave与Std并把保存结果。算法的优化性能的好坏采用平均值(Ave)与标准差(Std)去衡量。平均值的大小代表了算法的收敛速度的快慢,算法的鲁棒性的优劣则由标准差的大小衡量,实验结果见表2、表3、表4及表5。 表2 基准函数测试结果1 表3 基准函数测试结果2 表4 基准函数测试结果3 表5 基准函数测试结果4 由表2至表4可知,ISSA,SSA与TGWO三种算法在求解单峰基准测试函数F1、F3时皆能收敛至函数最小值0且算法的稳定性强,WOA与DPSO算法则相对表现较差。在求解函数F2,F4,F5,F6时,Ave值与Std值可以清晰得到ISSA收敛精度与稳定性优于其余四种算法。在求解函数F7时,ISSA局部开发能力相比于TGWO算法表现较差,但明显优于SSA,WOA,DPSO其余三种算法。根据上述分析可得,ISSA能有效增强原算法的寻优性能与局部开发能力,并有效提高了SSA的全局收敛精度。 多峰基准测试函数含有多个局部高峰,优化算法求解时极易陷入局部最优,因此多峰基准测试函数通常用于测试算法逃离局部最优的能力。ISSA,SSA,TGWO,WOA在求解函数F8时皆能收敛到全局最优值,同时四种算法的稳定性也相对较优。求解函数F9时,ISSA与SSA没有收敛到函数最小值,但也明显优于其余三种算法。针对求解F11,F12函数时,其寻优精度显然高于其余四种算法且能很好地平衡算法全局搜索与局部开发。总体而言,ISSA在求解多峰函数时较于其它算法均表现更优,能更好地降低算法陷入局部最优的风险从而提高整体搜索速度。 为更直观显示实验对比分析结果,本文给出ISSA与其余四中算法在相同实验条件下得到的函数仿真曲线,见图3。 由图3可知,与另外四种算法相比,ISSA在函数F1,F2,F3上收敛速度更快。针对函数F4,F5,ISSA前期搜索速度较慢,但后期局部搜索速度明显优于SSA。求解函数F6时,ISSA收敛速度与精度略优于SSA。 图3 算法对比寻优曲线 根据上述实验数据可知,TGWO在求解F7时速度显然比其余四种算法更好,但由收敛曲线图可看出ISSA算法性能与TGWO接近。通过求解F8,F10函数结果也可看出ISSA收敛更快,从其余的收敛曲线也能清晰得到ISSA收敛速度与逃离局部最优的能力都优于SSA,TGWO,WOA,DPSO。 综上所述,改进后的算法在搜索中能有效改善全局寻优精度,提高了算法稳定性,并使算法具有较强的逃离局部最优的能力。 麻雀算法是模拟麻雀觅食行为的一种仿生智能算法,本文针对其寻优过程中精度不足的缺陷,并具有陷入局部最优的风险提出一种改进的麻雀算法。麻雀寻优前期实施反向学习策略以增加初始种群的多样性,从而增加全局搜索速度;在后期引入Sinusoidal map混沌思想以增强逃离局部最优的能力。通过求解12个基本测试函数并与其余四种智能算法进行比较,ISSA能有效提高算法的收敛精度,且提高整个搜索过程的搜索速度与稳定性。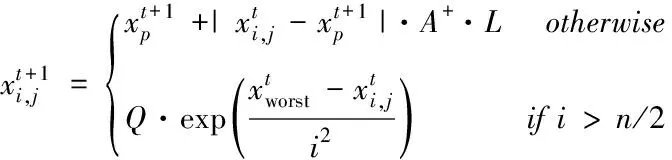


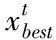

3 改进的麻雀算法
3.1 反向学习初始化种群
3.2 Sinusoidal map种群扰动
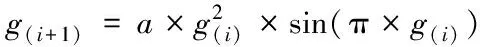
3.3 改进麻雀算法(ISSA)算法步骤


4 仿真研究
4.1 测试函数及对比函数

4.2 实验参数设置
4.3 实验分析



5 结语

