平纹织物逐层分离过程中的屈曲模拟与分析
王 楠, 苏军强
(江南大学 a.纺织科学与工程学院; b.设计学院,江苏 无锡 214122)
在服装智能制造升级转型的探索中,如何实现对裁片的自动控制(自动抓取、定位、缝边折叠等)是核心问题,国内外很多缝制设备企业都在大力投入、试图攻克这个难关。在各种探索方案中,一种能够实现对服装裁片“准确抓取、逐层分离、平展落料”的工程技术是核心需求之一,相关学者和工程技术人员进行了富有成效的探索,如SU J Q等[1-2]探究了软体机械手逐层分离裁片的影响因素,提出软体机械手的裁片单点抓取及多点布局抓取模型。从以上研究可以看出,基于仿生学设计的软体机械手表现出了较好的抓取界面友好性,成为诸如服装面料这类软体材料自动抓取及其自动化加工的重要研究方向。
在利用机械手进行纺织品裁片抓取和自动分离的相关研究中,沈津竹[3]发现软体机械手通过使织物“起拱”从而实现裁片的逐层分离,通过大量抓取实验确定了软体机械手的指间距、裁片受到的正压力是影响织物起拱高度最重要的因素,并通过建立数学模型的方法明确了各个影响因素之间的关系,但并没有明确指间距及压力影响“起拱”的内在机制。若要实现准确抓取、逐层分离的目标,需要进一步明确织物在逐层分离过程中屈曲变形的影响因素及作用原理。在有关织物屈曲变形行为的研究中,El Messiry M等[4]建立了织物临界屈曲压缩力的计算公式,并通过实验证明织物临界屈曲力与其弹性模量有很好的相关性。Paul M等[5]分析得出织物成功分层需要满足的力学条件,结合Timoshenko的弹性屈曲理论,将织物建模为具有恒定横截面弯曲梁,通过公式推导计算,最终得出使织物屈曲所需的最小夹持力。
在软体机械手逐层抓取织物过程中,由于上下两层甚至更多层织物相互之间会产生摩擦,导致织物在被软体机械手抓取过程中的屈曲行为变得非常复杂,因此通过实际抓取实验测试每层织物的受力大小及形态变化将比较困难。而有限元方法能够在模拟真实的织物逐层分离环境的基础上,对织物逐层分离过程进行定量分析,得出织物的受力大小及织物的屈曲高度随抓取参数的改变而发生的变化,从而进一步分析如何提高逐层抓取的准确率,节约实验成本。因此,本文尝试构建软体机械手抓取织物的模型,选取了织物屈曲高度这一个影响抓取成功率的主要指标,通过有限元方法分析纱线弹性模量、抓取机构施加的正压力、机械手设定的初始指间距对平纹织物分层过程中屈曲变形的影响。最后,通过实验验证了有限元方法应用于织物逐层分离过程分析的可行性。
1 织物逐层分离
织物抓取分离系统由软体机械手、空气驱动器、气管等组成,如图1所示。织物逐层分离时所使用的软体机械手通常为仿鸟喙结构,这类机械手可分为进气端、驱动端及夹持端三部分,其中进气端通过气管与空气驱动器连接,驱动端内有空腔。当空气驱动器通过气管向腔内输入正压,夹持端张开,输入负压,夹持端闭合,从而软体机械手能够实现对织物的抓取及释放。
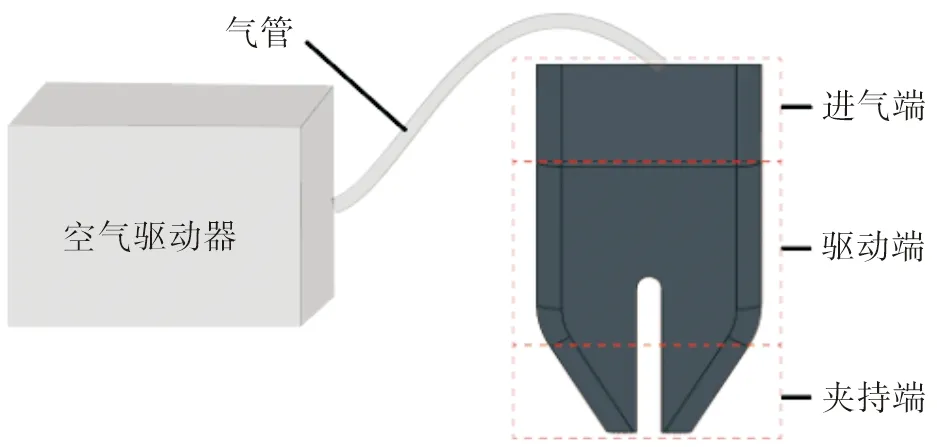
图1 软体机械手工作原理Fig.1 Working principle of soft manipulator
1.1 织物屈曲变形
夹持端在正压的作用下张开一定距离,然后向下移动并与织物接触,接触点为G1和G2,随后机械手继续下移,对织物施加垂直于织物平面的载荷FN。在压力的作用下,夹持端之间的织物产生屈曲,第一层织物的初始屈曲长度为Wmax,初始屈曲高度为H0,如图2所示。
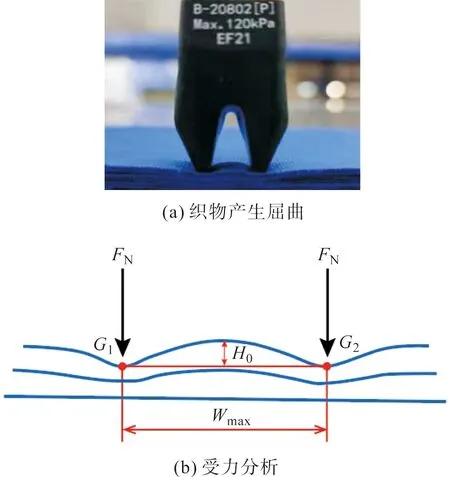
图2 准备抓取Fig.2 Preparation for grasping
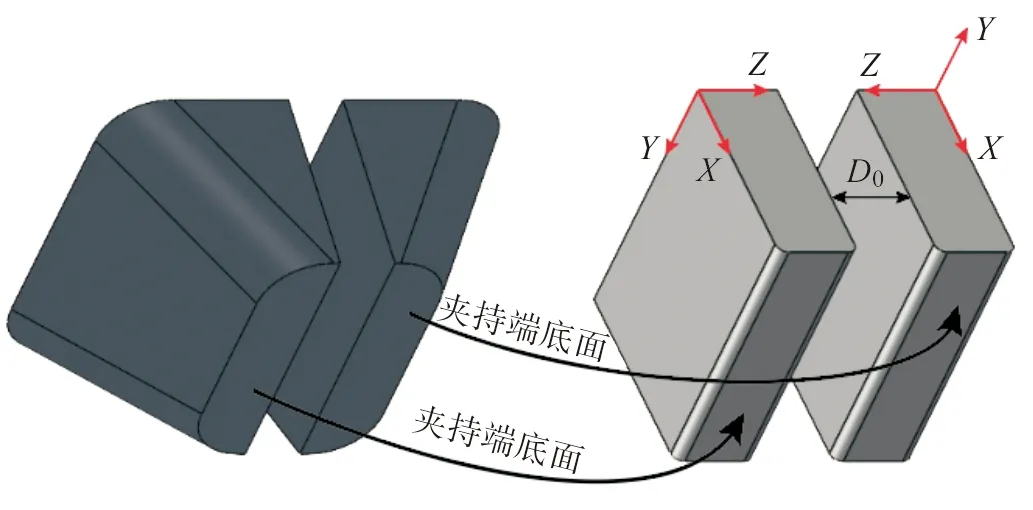
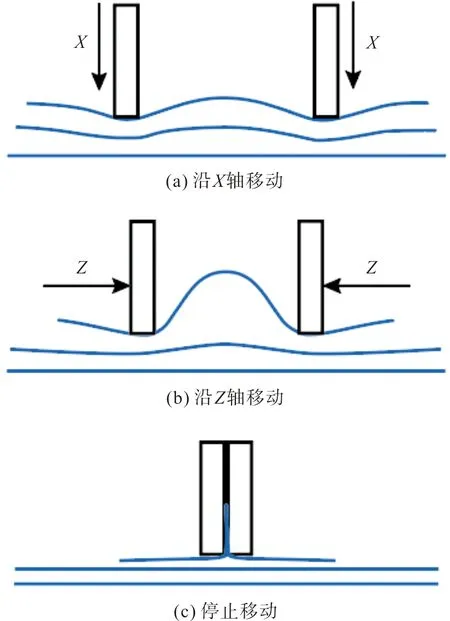
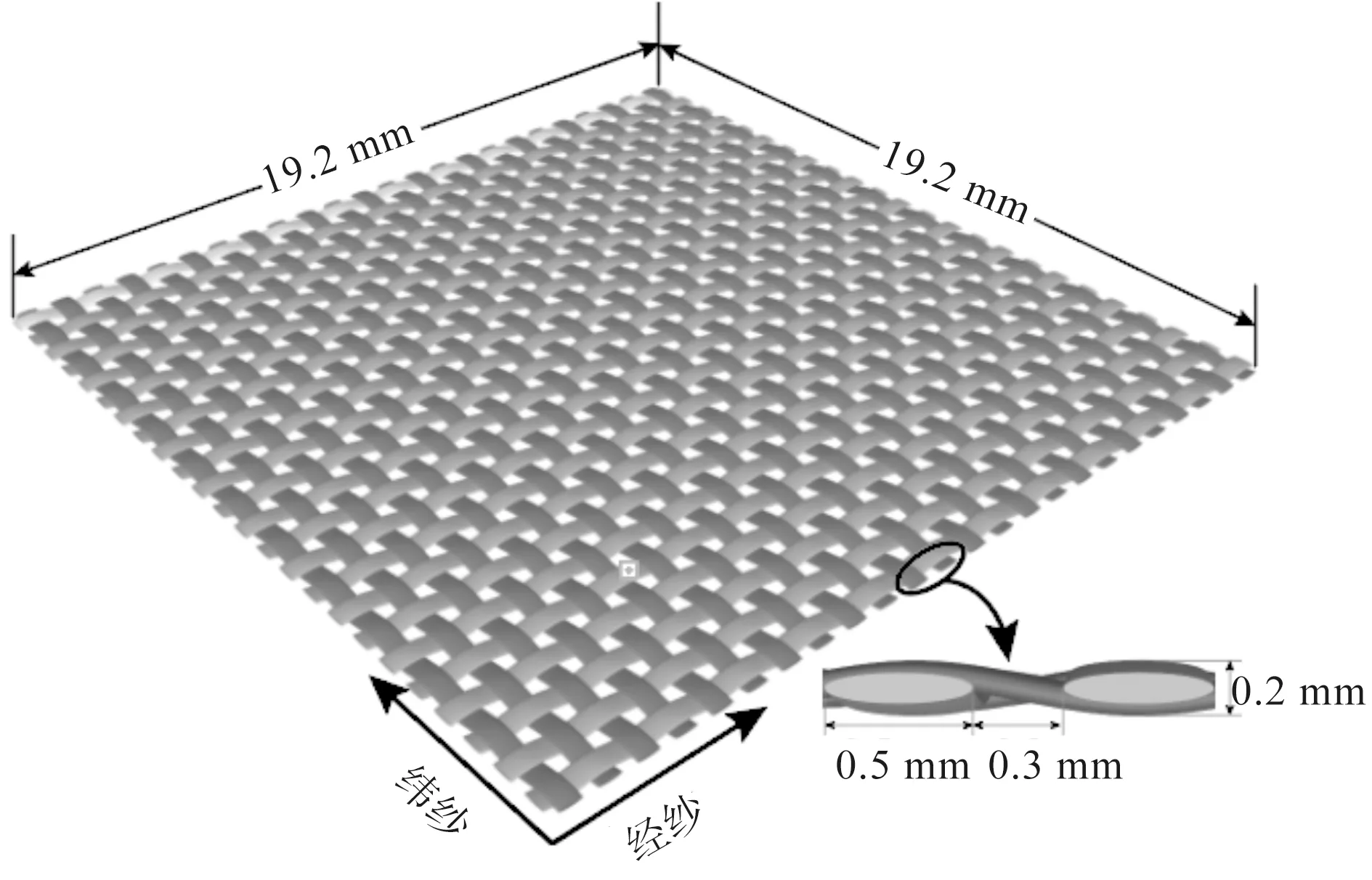
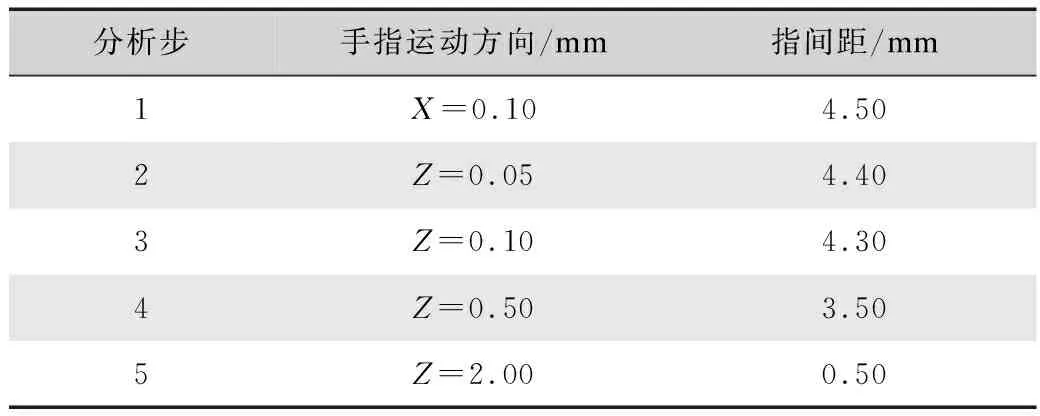
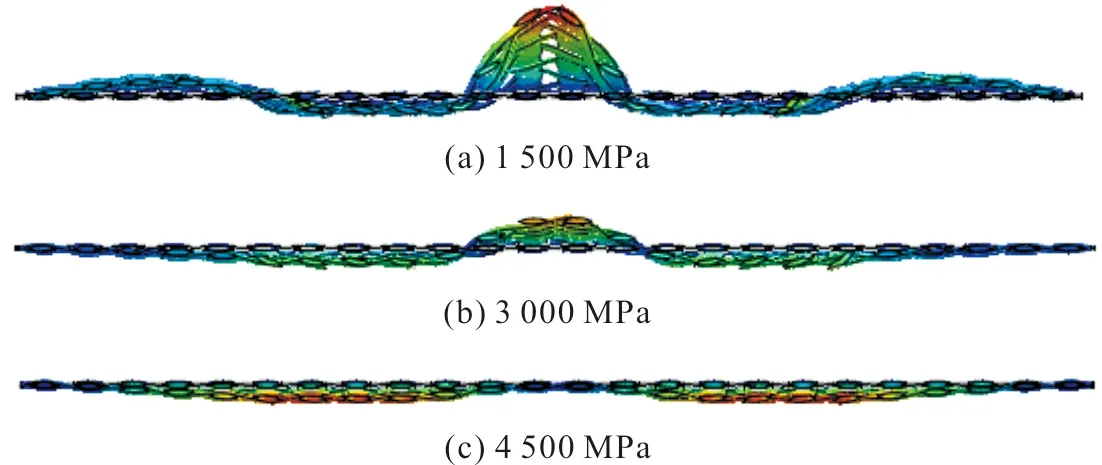
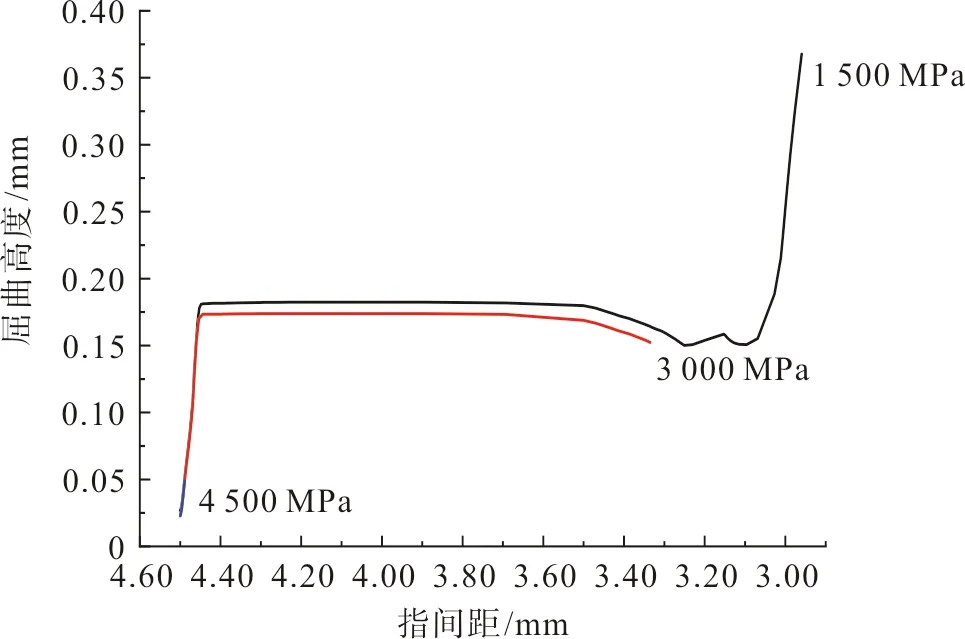
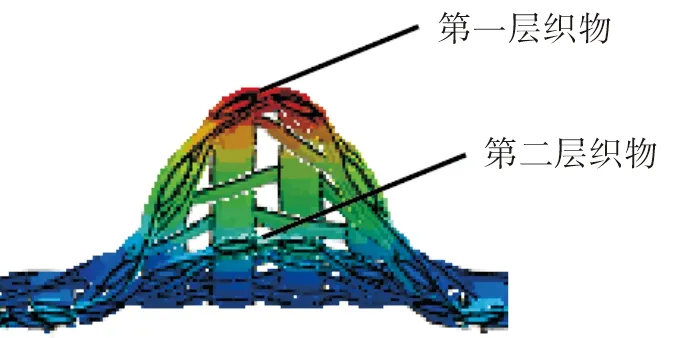
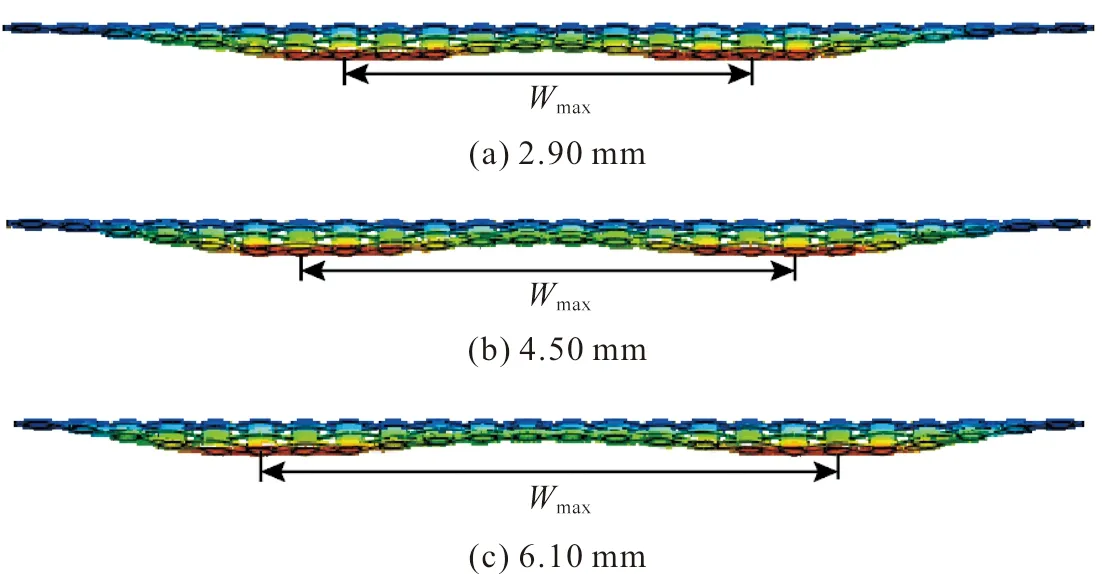
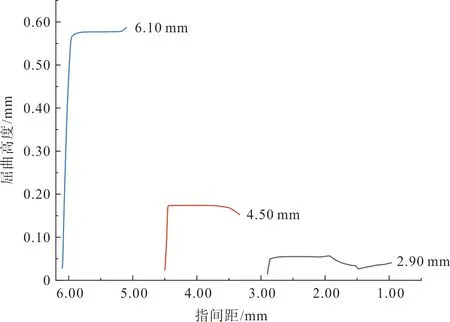
在空气驱动器输出的负压载荷Fg的作用下,夹持端逐渐闭合。由于压力FN的作用,手指与织物之间存在摩擦力Fgf,当Fgf>P+Fff且Fg 图3 夹持端逐渐闭合Fig.3 The gradual closing of the clamping part 当夹持端完全闭合,织物的G1与G2点重合于G点,成功被手指夹住,如图4(a)所示。此时织物的屈曲高度达到最大值Hmax,如图4(b)所示。Hmax的大小直接决定了夹持端能否夹住织物,从而实现分层。 图4 抓取一层织物Fig.4 Grasping a piece of fabric 在织物被抓取的过程中,只有机械手的夹持端底面直接作用于织物。准备分层时,夹持端底面与织物直接接触,并对织物施加垂直于织物平面的面载荷,使织物屈曲;分层过程中,夹持端的底面与织物之间的摩擦力推动织物的屈曲部分继续变形。因此,在模拟织物被逐层抓取过程中的屈曲行为时,只需考虑软体机械手的夹持端对织物的作用,夹持端的不规则几何体可简化为长方体。在夹持端建立坐标系如图5所示,夹持端为张开状态,初始指间距为D0。 图5 建立坐标系Fig.5 Establishing a coordinate 在此基础上,软体机械手逐层分离织物的动作可分为以下三步:1) 夹持端沿X轴正向移动,对织物施加一定的压力,织物产生屈曲,如图6(a)所示。2) 夹持端沿Z轴正向移动,织物屈曲高度逐渐增加,如图6(b)所示。3) 织物屈曲高度达到最大值,夹持端停止移动,如图6(c)所示。 图6 软体机械手抓取动作分解Fig.6 Decomposition of grasping action of the soft manipulator 由此可见,织物在被抓取过程中的屈曲变形处在不断变化之中,夹持端的初始指间距D0及在X轴方向的位移是影响织物屈曲变形的关键因素。 ABAQUS是国际上最先进的大型通用有限元软件之一,可以通过数值近似和离散化,将一个连续的介质离散成数个简单的几何单元,然后将实验测得的材料属性、载荷、接触等求解的基本条件赋予到每个单元上,最后求出偏微分方程边值问题近似解,计算精度高,适合织物、橡胶等非线性变形行为的模拟与分析。有限元分析在纺织领域的主要应用有织物的力学分析及热传递分析等[6-7]。 织物模型可分为宏观模型与细观模型两类,前者将织物看作具有一定厚度的薄板,这种建模方式运算效率较高,但忽略了织物内部纱线的运动。而细观模型是将纱线视为织物的最小组成单位,通过建立纱线模型,模拟织物中的经纬交织规律进行装配,从而形成织物模型。从纱线维度建立的细观模型虽然计算代价较大,但可以通过对纱线横截面和径向赋予不同的材料属性,更好地模拟织物屈曲时的真实状态[8],因此本文选用细观模型。 纱线几何模型的建立借助Texgen织物仿真建模软件完成。Texgen是由英国诺丁汉大学研究开发,既可通过输入织物内经纱与纬纱数量、相邻两根纱线间的距离、纱线截面宽度、织物厚度等参数自动生成织物模型,也可通过定义纱线横截面及纱线在织物中的成纱路径来实现单根纱线的建模[9]。常用的纱线截面形状有圆形、矩形、凸透镜形、跑道形、椭圆形等,如图7所示。其中,圆形和矩形截面虽然建立模型比较简单,但与实际织物截面形状还存在着较大的差距;椭圆形、跑道形和凸透镜形截面更符合纱线在织物中的形态[10]。为避免由于纱线间的接触过盈和接触不充分引起的计算不收敛[11],本文以平纹织物为例,建立的纱线模型采用椭圆形截面,得到如图8所示的织物细观模型。 图7 纱线截面形状Fig.7 Cross section of yarns 图8 织物细观模型Fig.8 Microscopic model of fabrics 由于面料印染过程中存在匹差、缸差、段差的色差问题,为保证服装的整体色差在可接受范围内,在服装生产工艺要求中,需要保证缝合形成一件衣服的裁片来自铺料过程中的同一层面料。这就要求,在软体机械手抓取裁片堆垛的过程中,必须保证逐层分离,“抓空”(即某次抓取不成功)或者“抓多”(即一次抓取了两层及两层以上的面料)都不能满足服装生产工艺要求,预示着抓取任务的失败。因此抓取模型中设置三层织物较为合适,第一层织物与夹持端底面直接接触,第三层织物与工作平面直接接触,如图9所示。 图9 织物逐层抓取模型Fig.9 Model of grasping fabrics layer-by-layer 2.3.1 织物材料 设定纱线为横观各向同性材料,材料方向如图10所示。在各向同性平面p(X-Y平面)内,材料各点的力学性质相同,而在垂直于p的平面t(X-Z、Y-Z平面)内,材料各点力学性质不同。即纱线横截面内弹性性质相同,而沿纱线径向(轴Z)材料性质不同。可通过弹性模量E、剪切模量G、泊松比v定义横观各向同性材料属性[12]。 图10 纱线材料方向Fig.10 Material direction of yarn 横观各向同性材料应力与应变之间的关系为: (1) 式中:弹性模量E1=E2=EP,剪切模量G13=G23=Gt,泊松比v31=v32=vtp,v13=v23=vpt。 剪切模量、弹性模量与泊松比的关系:Gp=Ep/[2/(1+vp)]。 2.3.2 夹持端材料 软体机械手多采用复合硅胶制作,复合硅胶是一种近似不可压缩的超弹性材料,即该物体在压力作用下体积几乎不发生改变。常用的超弹性材料本构模型有Mooney-Rivlin模型、Yeoh模型和Ogden模型等[13]。 本文采用Yeoh本构模型定义软体机械手材料的应力-应变关系。Yeoh模型为3阶多项式缩减模型,其本构关系可表示为: (2) 假设材料为完全不可压缩,则Je1=0,式(2)可化简为: U=C10(I1-3)1+C20(I2-3)2+C30(I3-3)3 (3) 式中:C10表示初始剪切模量,C20表示中等变形时材料软化,C30表示材料在大变形时硬化;I1、I2、I3分别为第1、第2、第3阶应变不变量,Je1为弹性体积比[14]。 ABAQUS有限元分析包括前处理、分析计算和后处理三个步骤。前处理中各项参数的合理设置是保证模型分析结果可信度的关键。 2.4.1 分析步与载荷 基于对软体机械手抓取织物的动作分析,在装配手指时改变两指之间的距离以模拟手指在不同气压下的指间距。在ABAQUS软件的Load模块中,通过改变数值的大小及正负实现对手指运动距离及运动方向的控制。 本文设置夹持端初始指间距为4.50 mm,首先沿X轴移动0.10 mm,对织物施加压力,随后沿Z轴移动2.00 mm,带动织物屈曲部分继续变形(为避免计算过程的不收敛,沿Z轴方向移动2.00 mm分成4个分析步依次赋值给夹持端模型),如表1所示。 表1 编辑边界条件Tab.1 Editing boundary conditions 2.4.2 网格划分 有限元分析通过划分网格将模型分成多个小单元,通过对每一个单元假定一个近似解,然后才能推导求出整个模型的近似解。网格划分的质量对计算精度至关重要,根据分析需求可将网格划分为线性单元、二次单元等不同的单元类型。 在网格模块中划分模型网格,如图11所示。本文中织物模型采用C3D10MH十结点修正二次四面体单元,每层织物被划分为13 824个单元,夹持端模型采用C3D8RH八节点线性六面体单元,与织物接触的部分单元类型选择C3D10MH十结点修正二次四面体单元,每个手指共有3 681个单元。为避免主面(软体机械手)穿透从面(织物),本文设置主面与从面接触部分的网格大小相等。 图11 网格划分Fig.11 Mesh generation 在本实验中,夹持端的初始指间距设定为4.5 mm,在接触织物后继续下移0.06 mm。实验所设定的纱线的弹性模量分别为1 500、3 000、4 500 MPa,计算结束时织物的屈曲变形如图12所示。随着纱线弹性模量的增加,织物的最大屈曲高度减小。由图13可知,在织物厚度相同、初始指间距一致的情况下,夹持端下移的距离相同,则织物的初始屈曲高度基本相等,即织物的初始屈曲高度H0与纱线模量没有明显的相关关系。 图12 不同弹性模量下织物的变形Fig.12 Deformation of the fabric with different elastic modulus 图13 屈曲高度与纱线弹性模量的关系Fig.13 Relationship between the buckling height andthe elastic modulus of yarn 当纱线弹性模量为1 500 MPa时,随着手指闭合,手指与织物之间的静摩擦力作用于变形部分的两端,使织物的屈曲高度逐渐增加而宽度减小,当指间距为3 mm时,织物的屈曲高度达到最大值。 当纱线模量为3 000 MPa时,织物的屈曲高度随着指间距的减小呈现先增加后减小的趋势。这是因为在指间距由3.5 mm减小到0.5 mm的过程中,手指开始与织物产生滑移,同时由于手指对第一层织物的压力不变,所以织物的屈曲高度反而下降。 当纱线模量为4 500 MPa时,织物的屈曲高度几乎不随着指间距的减小而增大。这是因为随着纱线弹性模量增加,织物抵抗屈曲变形的应力增加,从而使得Fgf 在本实验中,夹持端的初始指间距设定为4.50 mm,纱线弹性模量为3 000 MPa。夹持端沿X轴方向的位移分别为0.06、0.08、0.10 mm,第一层织物受到的压力分别为6、16、28 N,同时第二层织物受到的压力也在增加,与第一层织物受到的压力基本相等。计算结束时,不同压力下的织物最大屈曲变形如图14所示,随手指下移距离的增加,第一层织物受到的压力增加,织物的最大屈曲高度先增加后趋于不变。 图14 不同压力下织物的屈曲变形Fig.14 Buckling deformation of the fabric under different pressures 由图15可知,随着第一层织物受到的压力增加,织物的初始屈曲高度先增加后降低,X=0.08 mm时,织物的初始屈曲高度最大。当手指闭合时,屈曲高度随着指间距的减小呈现不同的趋势。 图15 屈曲高度与夹持端下移距离的关系Fig.15 Relationship between the buckling height and the downwarddisplacement distance of the clamping part 当X=0.06 mm时,第一层织物受到的压力为6 N。随着指间距的减小,织物的最大屈曲高度约为压力28 N时的1/3。这是因为织物受到的压力较小,在手指闭合的过程中,手指与织物之间的静摩擦力减小,不利于克服织物的屈曲力,从而织物的屈曲高度降低。 当X=0.08 mm和0.10 mm时,第一层织物受到的压力分别为16 N和28 N,但织物的最大屈曲高度基本相等。这是因为第二层织物受到的压力同样随着手指下移距离的增加而增加,因此第二层织物也在压力的作用下屈曲,阻碍了第一层织物的屈曲变形,如图16所示。 图16 第二层织物的屈曲变形Fig.16 Buckling deformation of the second layer fabric 在本实验中,纱线弹性模量为3 000 MPa。手指沿X轴方向的位移为0.06 mm,手指的初始指间距D0分别设定为2.9、4.5、6.1 mm。如图17所示,随着指间距的增加,织物的屈曲长度Wmax增加。计算结束时织物的变形如图18所示,随着初始指间距的增加,夹持端之间的织物最大屈曲高度Hmax增加。 图17 不同指间距下的织物的初始屈曲长度Fig.17 Initial buckling length of fabric withdifferent finger’s opening widths 图18 不同指间距下织物的屈曲变形Fig.18 Buckling deformation of the fabric underdifferent finger’s opening widths 由图19可知,当初始指间距为2.9 mm时,随着手指的闭合,夹持端之间的织物屈曲高度先增加后逐渐减小,织物的变形集中在织物的边缘部分。 图19 屈曲高度与初始指间距的关系Fig.19 Relationship between the buckling height and theinitial finger’s opening width 当初始指间距为4.5 mm时,随着手指闭合,织物的屈曲高度先快速增加,之后随着指间距的继续减小,夹持端与织物之间开始滑移,夹持端之间的织物屈曲高度略有降低。 当初始指间距为6.1 mm时,随着手指闭合,织物的屈曲高度先快速增加,之后随着指间距的继续减小,增加速度大幅降低。但总体来说,随着指间距的减小,织物的屈曲高度一直呈上升趋势。 对于给定的织物,初始指间距越大织物的初始屈曲长度越大。随着手指闭合,织物能够达到的屈曲高度最大值越大。这符合Euler材料屈曲变形理论,即材料的临界屈曲力与变形长度的平方成反比。指间距减小使得织物初始屈曲长度Wmax减小,织物抵抗屈曲变形的力越大,屈曲变形部分的两端G1、G2不能在Fgf的作用下向中间移动。 为验证有限元模型的有效性,本文选取了三种不同风格的平纹织物,并将其分别裁剪成长220 mm,宽80 mm的裁片各50片,如图20所示。软体机械手选用B-20802[P](指间距2.00~9.90 mm),在面料分层测试台(图21)上进行织物抓取实验,并统计分层准确率。 (4) 式中:A表示分层准确率,t表示抓取一层裁片的次数,n表示待抓取的裁片数量。 图20 三种不同风格的平纹织物Fig.20 Three plain fabrics with different styles 图21 面料分层测试台Fig.21 Test platform for fabric grasping 由图22(a)可知,随着夹持端沿X轴方向位移的增加,试样1和3的分层准确率增加,且增速逐渐平缓,而试样2的分层准确率先增加后下降。由图22(b)可知,随着指间距的增加,织物的分层准确率增加。即在一定范围内,随着正压力和初始指间距的增加,织物的最大屈曲高度增加,从而织物更易被逐层分离。这与有限元分析得出的规律一致,证明了有限元方法应用于织物逐层分离分析的可行性。 图22 织物逐层分离准确率Fig.22 Accuracy of separating fabrics layer-by-layer 本文建立了织物和软体机械手模型,采用ABAQUS有限元分析软件对软体机械手逐层抓取织物的过程中织物的屈曲形态变化进行了模拟。结果显示,纱线的弹性模量越大,织物越不易屈曲变形。随着第一层织物受到的压力的增加,织物的最大屈曲高度先快速增加而后趋于平缓,主要原因是在分层过程中总有多层织物在相互制约,不能只考虑单层织物的受力情况。随着初始指间距的增加,两指之间的织物变形长度增加,织物更易屈曲变形,从而织物的最大屈曲高度增加,这一点符合Euler材料屈曲变形的规律。最后测试不同抓取参数下织物的分层准确率,结果表明,在一定范围内,随着正压力和初始指间距的增加,织物的最大屈曲高度增加。因此在利用软体机械手逐层分离织物时,可以增加织物受到的正压力,或通过调节气压以增大软体机械手的初始指间距,从而提升织物逐层分离的准确率。 《丝绸》官网下载 中国知网下载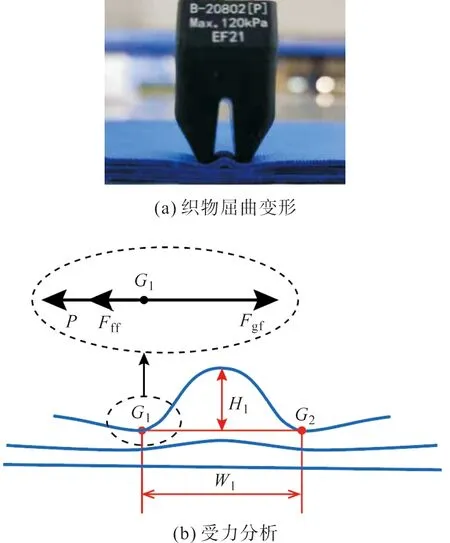

1.2 软体机械手动作分析
2 建立有限元分析模型
2.1 织物几何模型

2.2 逐层抓取模型

2.3 定义材料属性

2.4 有限元分析前处理

3 有限元计算结果分析与验证
3.1 纱线弹性模量对织物屈曲高度的影响
3.2 压力对织物屈曲高度的影响
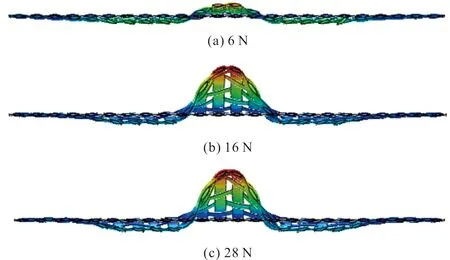
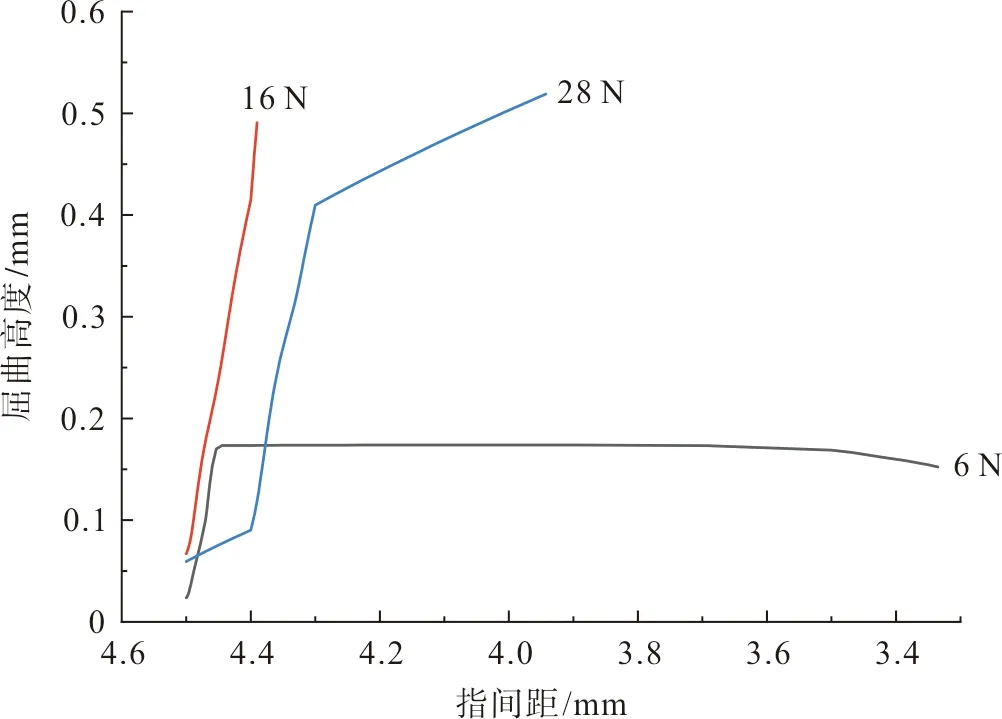
3.3 初始指间距对织物屈曲高度的影响

3.4 实验验证




4 结 论



