政企协同视角下应急物资储备库选址优化研究

刘博，徐晓敏

(北京信息科技大学 信息管理学院，北京 100085)

0 引言

在国家应急体系中，应急物资储备库选址是其中的重要一环，选址是否合理直接关系到社会经济效益和国家防灾减灾系统的运行效率[1]。目前我国应急物资储备主要以政府为主，储备主体单一。为提高应急救援效率，必须建立更多储备库以保证应急物资的及时、准确供应，但这无疑会造成成本增加,而企业拥有常态化、稳定的物资储备可以成为应急物资保障强大的后备力量。2020年我国抗击新冠肺炎疫情时，企业在政府统一指挥协调下积极参与到应急物资供应中，表明企业已经成为应急物资保障体系中不可忽视的重要组成部分。为实现政府+企业应急物资储备库的合理布局及有效协同，有必要专门针对政企协同视角下应急物资储备库优化选址决策问题进行研究。

关于政府应急物资储备库选址的研究，郭子雪等[2]首次提出了区间的概念，通过区间数建立了选址模型；俞武扬[3]考虑灾害发生后服务能力受到损害的情况，建立了覆盖程度最大化模型；Ferrari等[4]在进行救护站选址研究时，综合考虑覆盖面积、储备库数量以及距离3方面因素构建了多目标选址模型；陆相林等[5]考虑了交通方式、需求点风险程度等因素，以总满意程度最大化为目标建立选址模型。针对政企协同储备的研究成果主要以定性研究为主。于冲等[6]在深入分析我国现有应急物资储备模式的基础上，提出了政企协同储备模式，并提出相关措施和建议；王海兰[7]对战备物资协议企业合同准备模式进行了研究；刘阳等[8]对期权机制下的政企联合储备模型、利润分配机制进行了研究；庞海云等[9]结合期权契约的特点对应急物资特性进行分析,构建政府期望成本函数和企业期望利润函数,提出了政企联合储备模型。

目前针对单一政府应急储备库选址的研究成果相对丰富、完善，而关于应急物资的政企协同管理问题的研究尚处于起步阶段，定量研究成果相对较少。本文针对政企协同储备，通过建立多储备主体、多级覆盖的多目标决策模型，研究探索政企协同视角下应急物资储备库选址布局的有效方法。

1 模型构建

1.1 研究思路

首先，在模型中加入备选企业储备库相关参数和变量，考虑政府和企业主体在应急响应时间和成本方面优势的不同，构建多目标优化模型；其次，综合考虑人口、社会、灾害多方面因素构建需求指标体系，对需求水平进行分析；最后，通过NSGA-II算法对模型进行求解，得出选址方案。

1.2 模型假设

1)主要研究静态选址问题，仅考虑一个区域内从储备库到可能需求点的两级网络；

2)各备选储备库以及需求点的位置已知，采用城市间的中心距离进行计算；

3)不考虑突发事件发生后道路损坏应急物资无法送达的情况；

4)突发事件发生后企业储备库直接向需求点供应物资，无需运送至政府储备库；

5)突发事件发生后应急物资运输方式为单一公路运输且车辆的平均行驶速度已知；

6)每个储备库可同时为多个需求点提供服务，但每个需求点最多只能分配给一个政府储备库或企业储备库。

1.3 参数及变量设置

模型主要参数定义如下。

I:需求点的集合(i=1，2，…，m)；

Z:备选政府储备库的集合(z=1，2，…，n)；

Q:备选企业储备库的集合(q=1，2，…，p)；

wi:各需求点的需求权重；

v:车辆平均运行速度；

cz:备选政府储备库开放启动成本；

cq:政府给予备选企业储备库的补贴价格；

tz或tq:备选政府或企业储备库的响应时间；

pz或pq:开放政府或企业储备库的数量；

rz或rq:备选政府或企业储备库的覆盖半径；

lzi或lqi:备选政府或企业储备库至需求点i的距离；

T:加权时间；

C:政府初始成本。

模型决策变量：

xz= 1，备选政府储备库z被选中，否则为0；

xq= 1，备选企业储备库q被选中，否则为0；

yzi= 1，备选政府储备库z向需求点i供应应急物资；

yqi= 1，备选企业储备库q向需求点i供应应急物资。

1.4 模型建立

本文以加权时间最小化和政府初始成本最小化为目标，其中政府储备库作为应急物资储备的主要力量需要对所有需求点进行全覆盖，企业储备库作为补充，只需要对部分需求点进行二级覆盖。

1.4.1 目标函数

(1)

(2)

目标函数中：式(1)表示加权时间最小，第一项表示政府储备库到各需求点的加权运输时间和响应时间，第二项表示企业储备库到各需求点的加权运输时间和响应时间，体现应急救援效率；式(2)表示政府所付出的初始成本最小，第一项为开放政府储备库或完善现有政府储备库的费用，第二项为政府为激励企业参与应急物资储备工作以及弥补企业库存增加带来的风险与成本而给予协议企业储备库的补贴费用，是经济性制约。

1.4.2 约束条件

(3)

(4)

yzi≤xz∀i∈I,∀z∈Z

(5)

yqi≤xq∀i∈I,∀q∈Q

(6)

yzilzi≤rz∀i∈I,∀z∈Z

(7)

yqilqi≤rq∀i∈I,∀q∈Q

(8)

(9)

(10)

xz,xq,yzi,yqi∈{0,1} ∀i∈I,∀z∈Z,∀q∈Q

(11)

约束条件中：式(3)表示每个需求点都有且只有一个政府应急物资储备库为其服务；式(4)表示每个需要企业储备库供应物资的需求点有且只有一个企业应急物资储备库为其服务；式(5)表示各需求点只能由被选中的政府储备库覆盖；式(6)表示每个需要企业储备库供应物资的需求点只能由被选中的企业储备库覆盖；式(7)表示需求点到政府储备库的距离小于其覆盖半径；式(8)表示需求点到企业储备库的距离小于其覆盖半径；式(9)表示选择pz个政府储备库；式(10)表示选择pq个企业储备库；式(11)表示决策变量均为0或1。

2 模型求解方法

2.1 需求权重

在本文模型中wi是一个重要的参数，需求水平越大的需求点对救援时间的要求越高，需求点的权重也越大。现有文献对于应急需求权重的确定大多只考虑了人口这一因素，不够全面。本文通过构建需求指标体系使用熵权法确定各需求点的需求权重，从而使得求解方案更具有合理性。

2.1.1 构建指标体系

通过对影响需求水平的因素进行分析，构建应急需求水平指标体系，如表1所示。

表1 应急需求水平评价指标体系

2.1.2 确定需求权重

熵权法适用于指标数据客观真实且易获得的情景。该方法可得到相对客观的权重，能避免人为因素导致的误差。本文所有数据从相关统计数据中获取，通过熵权法计算各需求点的需求权重水平。

步骤1构建初始矩阵。构建评估矩阵A，其中aij为第i个需求点的第j项指标值。

步骤2标准化处理。将A转化为标准矩阵P，其中pij为经过无量纲化处理的第i个需求点的第j项指标值；maxaj、minaj分别为第j项指标的最大值和最小值：

本文所选取的指标均为正向指标，为避免标准化后的pij=0影响后续计算，对所有pij加0.000 1。此处理对最终结果无影响。

步骤3计算每一指标的熵值：

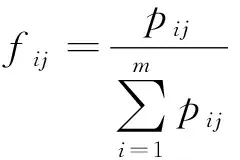
步骤4计算各指标的熵权：

步骤5计算各需求点的综合得分：

步骤6计算各需求点的需求权重：

2.2 模型求解算法

本文模型参数及决策变量个数较多，求解比较困难，因此选择智能算法进行求解。非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ)算法通过非支配排序操作将多目标转化为虚拟适应度，并通过精英选择策略来求解多目标优化问题。

步骤1编码设计。每条染色体由两部分组成：第一部分1至n位为1～n的随机排列，对应1～n个备选政府储备库，第二部分n+1至n+p位为1～p的随机排列，对应1～p个备选企业储备库，取第一部分编码的前pz个为开放的政府储备库，然后取第二部分编码前pq个为开放的企业储备库。

步骤2种群初始化。根据染色体编码规则产生一定数量的初始种群。

步骤3适应度计算。根据加权时间和政府初始成本计算与每个个体相适应的目标函数。

步骤4快速非支配排序。采用精英策略，依据目标函数的值进行非支配排序，当所有个体都有非支配层级时，停止排序。

步骤5选择、交叉和变异。采用二元锦标赛选择法，即每次随机选择2个个体，优先选择排序等级高的个体，如果排序等级一样，优选选择拥挤度大的个体；设置交叉和变异概率，对子代种群进行交叉、变异等操作产生新的种群。

步骤6迭代和终止。开始新一轮非支配排序、选择、交叉和变异。当迭代次数达到设定的最大值，算法终止，得到帕累托最优解集并输出结果。

3 模型实现

为验证模型与算法的可行性与有效性，以Matlab 2018b为工具通过实际算例对模型予以实现。

3.1 算例背景

假定湖北省计划选择8个政府储备库和2个企业储备库，为全省各需求点提供应急物资，其中政府部门计划对需求指标权重位于前5位的地区在政府储备库进行一级覆盖的基础上通过企业储备库进行二级覆盖，即这5个地区需要被选中的政府储备库和企业储备库进行2次覆盖，其他12个需求点均只需要被政府储备库覆盖1 次。

3.2 数据收集

各需求点相关数据从湖北省统计年鉴、湖北省各州市统计年鉴以及湖北省应急管理厅官网有明确记录的自然灾害发生次数获取，具体如表2所示。

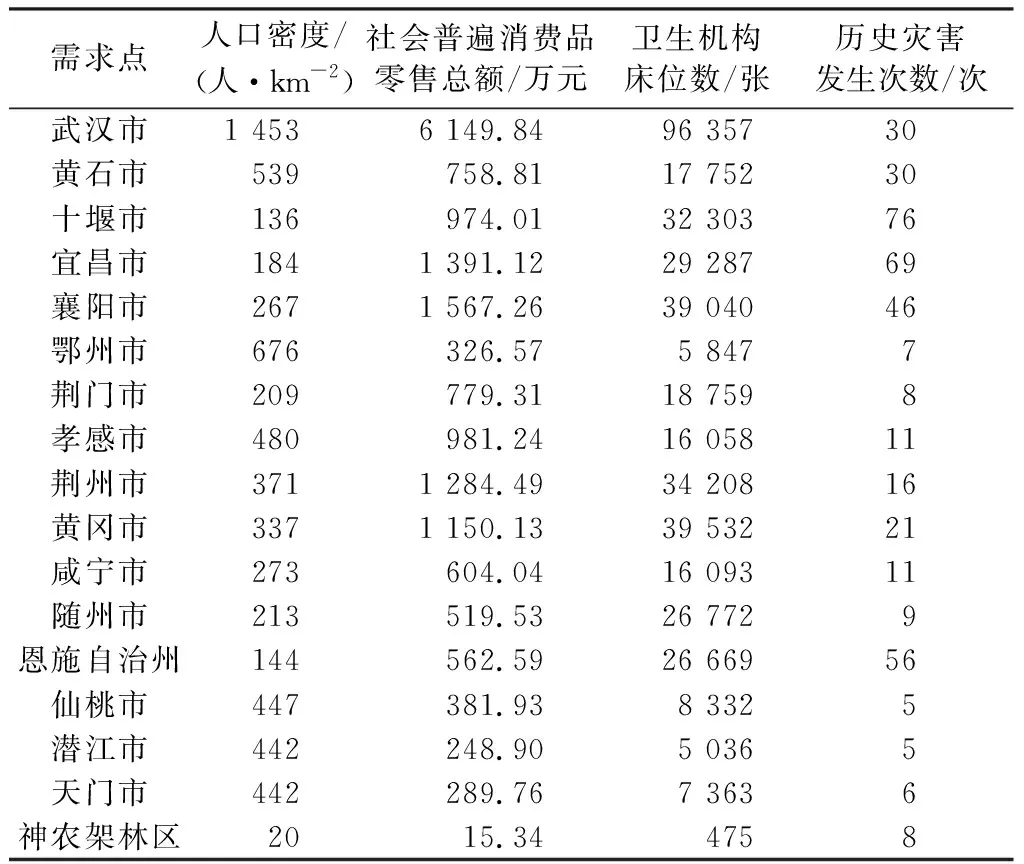
表2 各需求点各项指标原始数据

各备选政府储备库的启动成本、备选企业储备库补贴价格及响应时间参考现有研究资料进行假设，如表3及表4所示。

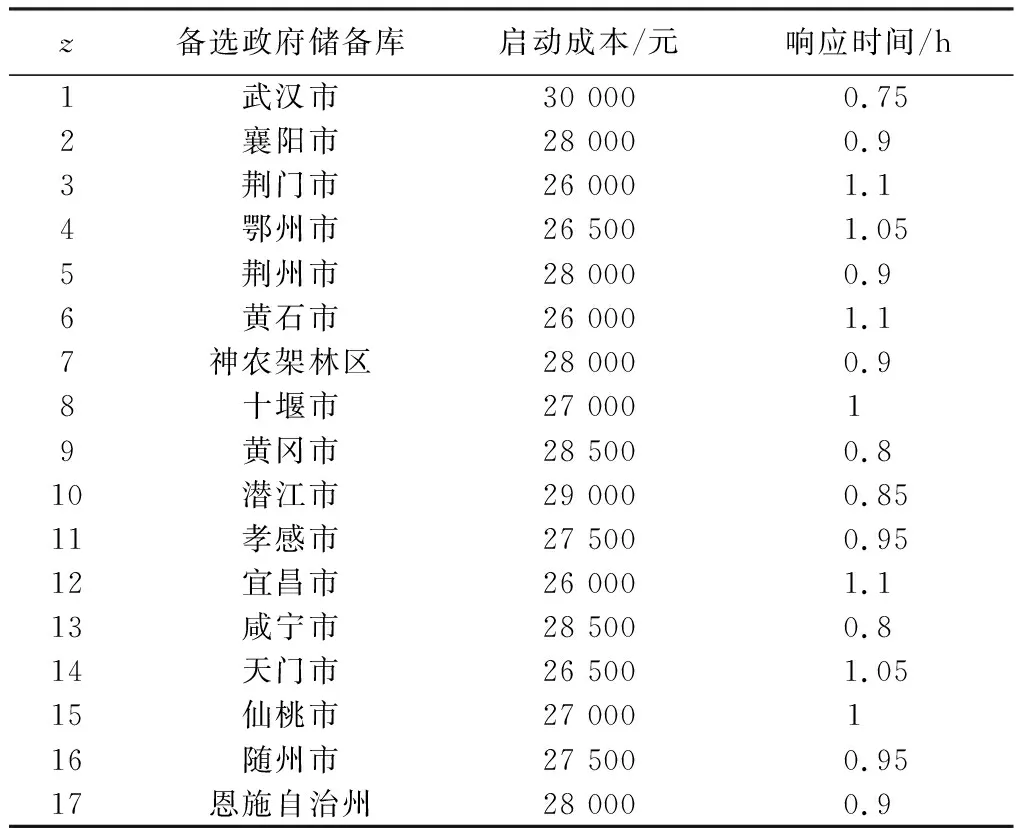
表3 各备选政府储备库相关参数

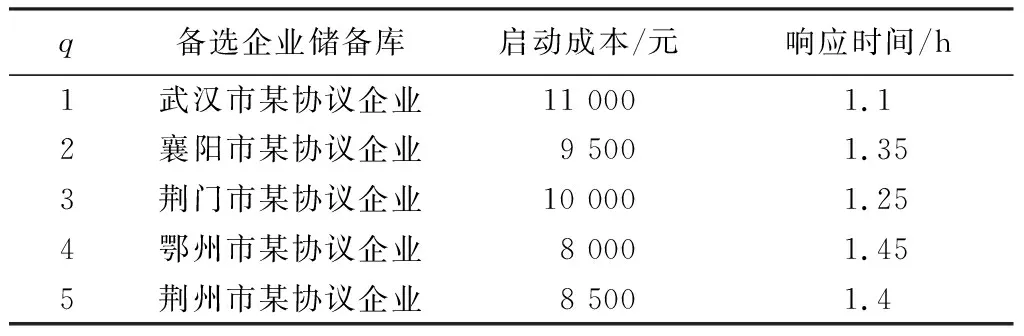
表4 各备选企业储备库相关参数

3.3 实现过程

3.3.1 需求权重确定

通过熵权法得到各指标的熵值与熵权，然后计算得到各需求点的综合得分及排名，进而得到其需求权重，具体数据如表5所示。

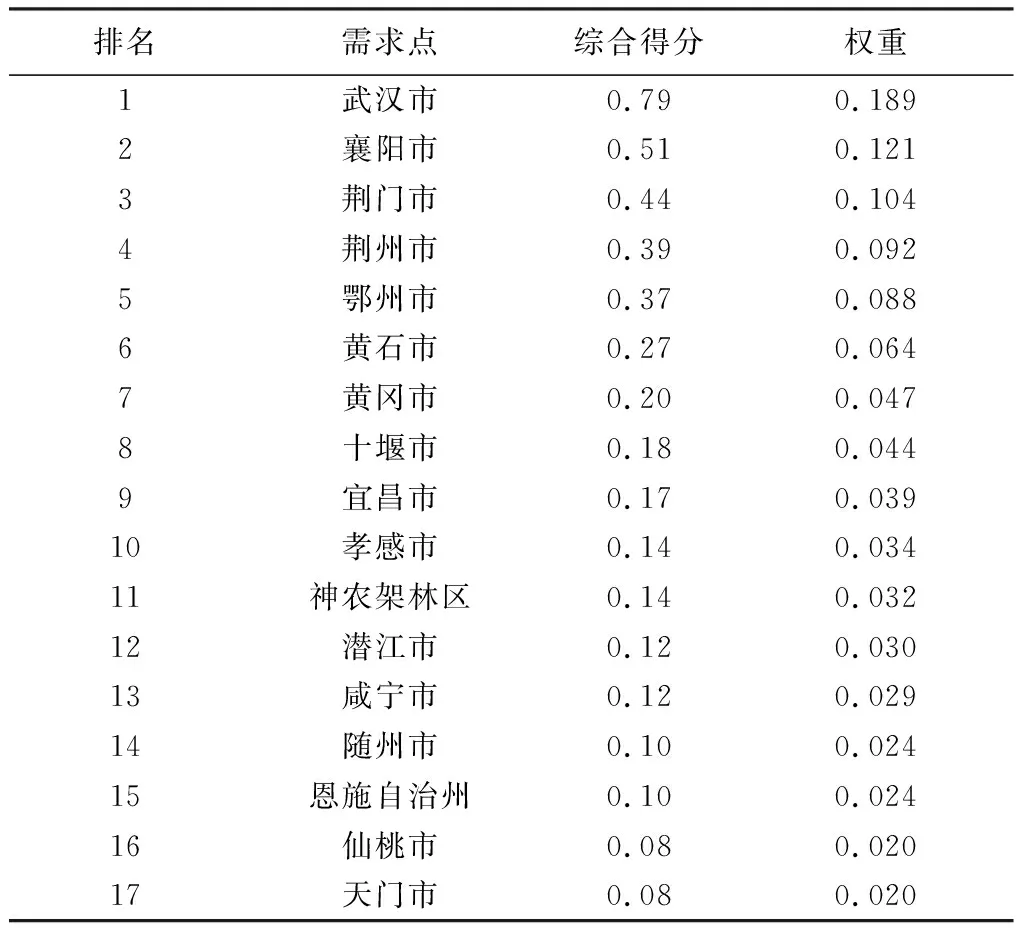
表5 各需求点综合得分及权重

3.3.2 选址优化求解

得到各需求点的需求权重后通过Matlab软件对本文模型进行求解。模型参数以及算法参数设置为：政府储备库和企业储备库覆盖半径均为300 km，车辆平均运行速度为80 km/h，种群数量为200，迭代次数为200，交叉概率为0.9，变异概率为0.1。

图1为本文模型运行结果，从求解结果可以看出加权时间和政府初始成本2个目标之间相互制约和关联，一个目标的上升会导致另一个目标的下降。因此，应急管理决策者在进行储备库综合决策时，可根据实际情况选择方案。

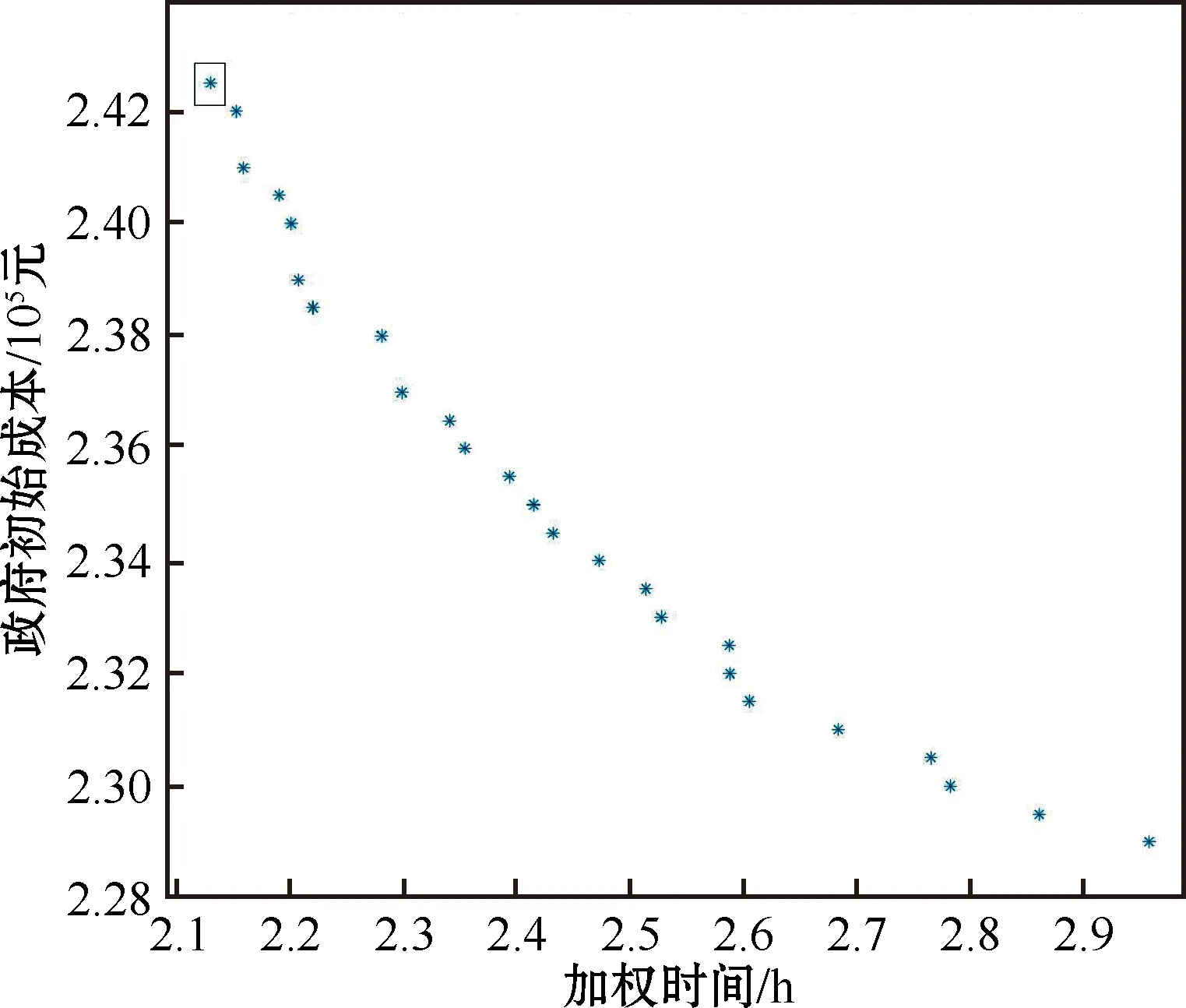
图1 本文模型帕累托最优解集

由于在应急救援中相对于经济性而言更注重时效性，因此选取解集中加权时间最小的方案进行分析，该方案开放表3中的第1、2、3、5、8、9、10、17个政府储备库以及表4中的第1、3个企业储备库，即开放武汉市、襄阳市、荆门市、荆州市、十堰市、黄冈市、潜江市、恩施自治州政府应急物资储备库，在武汉市和荆门市选择协议企业开放企业储备库，其中武汉市协议企业储备库分别与武汉市、黄冈市政府储备库进行协同为武汉市、鄂州市提供应急物资保障，荆门市协议企业储备库分别与襄阳市、荆门市、荆州市政府储备库进行协同为襄阳市、荆门市、荆州市提供应急物资保障，该方案加权时间为2.13 h，政府初始成本为242 500元。各储备库与需求点的对应关系如表6、表7所示。

表6 政府储备库与需求点的对应关系

表7 企业储备库与需求点的对应关系

4 比较分析

为验证本文模型的合理性及有效性，特选取同等备选数量的单一政府储备库选址优化方案进行对比分析：在本文模型的基础上剔除掉备选企业储备库，对需求指标权重位于前5位的地区在一个政府储备库进行一级覆盖的基础上，再选取一个政府储备库进行二级覆盖，得到单一政府储备主体选址模型(后文简称为“对比模型”)，其他所有参数设置相同，运行结果如图2所示。

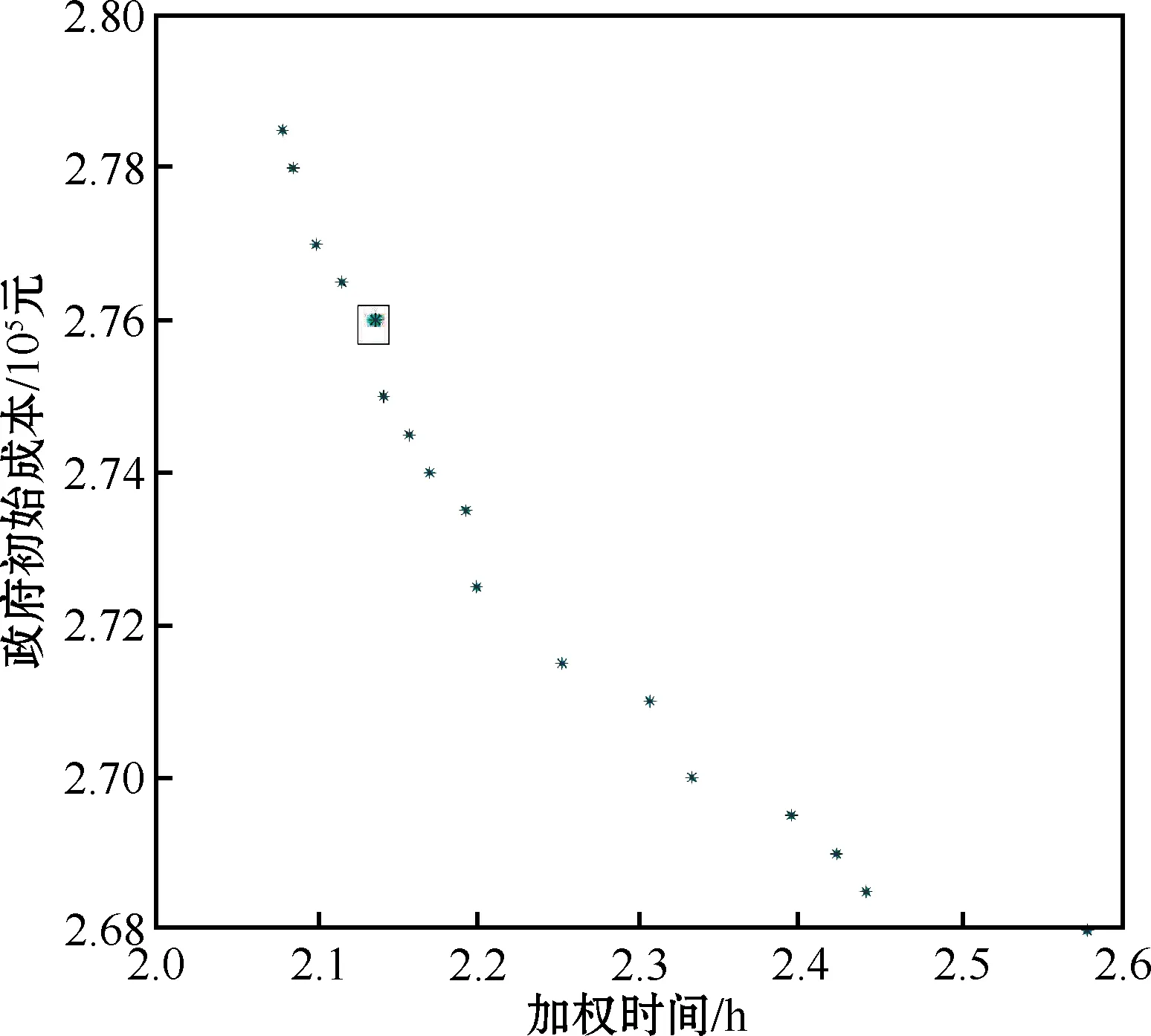
图2 对比模型帕累托最优解集

通过对比图1和图2分析发现：首先，在对比模型中，解集中加权时间的最小值(2.08 h)与最大值(2.58 h)均要小于本文模型加权时间的最小值(2.13 h)与最大值(2.96 h)。主要原因是：政府储备库自身应急响应平均时间要比企业储备库短，能够迅速响应灾情，在救援效率方面具有优势。其次，在图1中寻找本文模型加权时间最小的方案进行标注，并在对比模型中寻找与上述最小加权时间接近的点进行标注，两方案的目标函数值如表8所示，可以发现在加权时间相近情况下，本文方案的政府初始成本要小于单一政府选址方案的成本。主要原因是：由于协议企业参与，减少了政府储备库的个数，同时企业在物资管理和市场流通方面具有优势，使得企业平均补贴价格要低于政府自身开放储备库的成本。此外，对比图1及图2帕累托最优解集中解的数量(即点的数量)可以看出：图1中选址方案有25个，图2中选址方案有17个，政企协同视角下可供选择的方案更多。主要原因是：企业主体的加入不仅提升了储备能力，也为政府增加了更多可供选择的储备库，政府可以考虑利用企业储备库替代部分供应能力相对较差的政府储备库，为政府提供了更多可选择的方案。通过对比分析可以看出将企业储备库作为政府储备的补充能够在保证物资供应时效性的同时降低政府成本、丰富政府决策方案，政企协同视角下的选址研究具有现实意义。

表8 目标函数值对比

5 结束语

本文在进行应急物资储备库选址研究时，考虑了各需求地区需求水平的差异，对各地区赋予相应的需求权重，并在模型设计时中加入企业储备主体，建立了一个多储备主体、多级覆盖选址模型。研究结果表明政企协同是目前应急物资储备管理的一种有益方式，企业主体的加入可以有效弥补单一政府储备的不足，在保障应急物资供应时效性的同时降低应急成本，提高应急物资供给的效率和经济性。同时本文研究中的定量分析思路与方法是对应急管理科学化的有益探索。但在研究过程中只考虑了公路交通一种运输方式，在未来的研究中可以考虑多种交通运输方式来进一步对该研究进行完善。