直线超声电机无模型自适应多步预测控制

李一凡，曹荣敏，侯忠生，周惠兴

(1.北京信息科技大学 自动化学院，北京100192；2.青岛大学 自动化学院，青岛 266071；3.北京金铎科技发展有限公司，北京 100081)

0 引言

高速高精度直线超声电机运动平台是精密加工的核心部件，是目前精密加工领域的研究热点。高精度加工技术的发展对进给系统的要求越来越高，因此连续的微进给运动对于实现产品的最佳性能非常重要。直线超声电机作为一种新型的微特电机，具有定位精度高、断电自锁、运行响应速度快和结构简单的优点[1]。

由于直线超声电机在运行过程中表现出的非线性和时变特性，会给建立精确的数学模型带来很大的困难[2],所以在直线电机运动控制研究中通常使用一些无模型的控制方法，包括比例积分(proportional-integral,PI)控制、模糊控制、神经网络控制、自适应控制等。文献[3]建立了直线超声电机的非线性模型，提出非线性补偿比例积分微分(proportional-integral-derivative,PID)算法对直线超声电机进行定位控制；文献[4]提出一种PI控制加迭代学习控制的复合控制算法，基于直线超声电机平台模型进行设计，实验控制精度可达3.8 μm；文献[5]介绍了一种应用于非线性超声电机纳米位置控制的输出反馈自抗扰控制方案，利用自抗扰控制方法对直线超声电机进行位置控制。

针对直线超声电机位置控制的问题，本文基于无模型自适应预测控制(model-free adaptive predictive control,MFAPC)[6]理论，提出了无模型自适应控制和多步预测控制相结合的无模型自适应多步预测控制(model-free adaptive multi-step predictive control,MFAMPC)方法。无模型自适应控制仅需要使用受控系统的输入/输出(input/output,I/O)数据，避免了非线性系统控制需要建模的问题，从而防止模型误差对控制效果的影响。而多步预测控制算法可以提高直线超声电机的位置控制精度，相关研究较多，比如文献[7]利用汉默斯坦模型和实验测量方法对超声波电机进行了建模,设计多步模型预测控制器对电机进行位置控制；文献[8]基于超声电机动力响应的实验数据，利用粒子群优化方法得到了超声电机驱动系统的非线性汉默斯坦模型，提出了超声波电机的非线性广义多步预测速度控制策略；文献[9]提出一种将多步预测、滚动优化与迭代学习控制律相结合的迭代学习控制律设计方法，通过设计超声电机的非线性汉默斯坦模型，提出了一种电机的逆补偿方法，对直线超声电机进行位置控制。

本文所提方案结合了无模型自适应控制和多步预测控制的优点，设计并给出稳定性和收敛性证明，将该算法与其他数据驱动控制算法进行仿真结果对比，验证了无模型自适应多步预测控制方法在保证直线超声电机系统稳定和精度方面的有效性。

1 无模型自适应多步预测控制方法

1.1 动态线性化方法和多步预测方程

一般离散时间非线性非仿射系统可用式(1)描述[6]：

y(t+1)=f(y(t),y(t-1),…,y(t-ny),

u(t),u(t-1),…,u(t-nu))

(1)

式中：u(t)∈R、y(t)∈R分别为t时刻系统的输入和输出；ny、nu为系统的未知阶数；f(…)为未知的非线性函数。

无模型自适应多步预测方案与无模型自适应单步预测不同，需要对未来多个预测周期进行优化控制，存在多个输入输出反馈。系统(1)紧格式动态线性化的转换需要满足下面两个假设条件[6](为简化控制系统设计方案，减少控制器解算时间，对假设2进行了矩阵化改进)。

假设1除有限时刻点外，f(…)对控制输入u(t)有连续的偏导数。

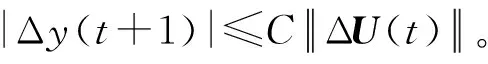
式中

其中：C是一个常数；L是一个正整数，称为线性化的控制输入长度常数。

定理1对于系统(1)，当假设1和2成立时，对于给定的L，当‖ΔU(t)‖≠0时，一定存在伪偏导数φ(t)∈R使得系统(1)可以转化为紧格式动态线性化方法表达式(2)：

(2)

式中

(3)

为进行无模型自适应多步预测控制，对式(3)矩阵化，令

式(3)可以改写为

x(t+1)=Ax(t)+BΔu(t)

(4)

Δy(t)=cT(t)x(t)

(5)

式中

将紧格式动态线性化表达式(4)、(5)写成一步预测方程的形式：

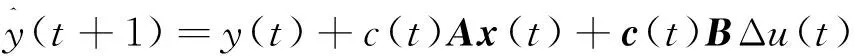
(6)

可以类似推出向前P步的预测方程如下：

(7)

将上述P步预测方程式(7)改写成如下矩阵形式：

Y(t+1)=[y(t+1)…y(t+P)]T

E=[1 1 … 1]T

x(t+1)=[Δu(t)…Δu(t+j-1)]T

控制系统输入和输出多步预测方程可简写为以下形式：

Ψ2(t)x(t)

(8)

1.2 控制律设计

在控制算法的设计中，考虑如下二次型控制输入准则函数：

(9)

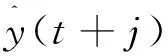
根据参考文献[10]，可得：

(10)

根据式(10)，式(9)可写为

(11)

将式(8)代入式(11)，利用性能指标(9)最优化条件∂J/∂Δu(t)=0,可得控制律为

[Y(t+1)-Ey(t)-Ψ2(t)x(t)]

(12)

根据预测控制求解控制量的基本方法，即所求得控制序列的第一个元素作为受控对象的实际控制量[11]，则可以得到该时刻的控制量如下：

u(t)=u(t-1)+gTx(t+1)

(13)

式中gT=[1 0 … 0]。

1.3 参数估计和预报算法

由于式(5)中参数向量c(t)未知，传统最小二乘法不能对未知参数进行估计。针对待估参数未知和提高控制算法的鲁棒性问题，本文引入两个干扰项ϑ、υ，同时对待估计参数进行了约束，利用递归最小二乘法确保所有信号在待估计参数具有不确定性时有界。参数向量c(t)通过如下改进的递归最小二乘法在线估计：

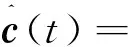
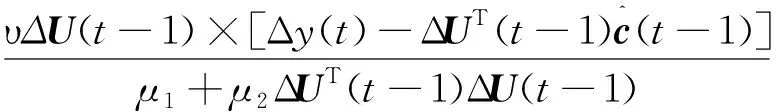
(14)

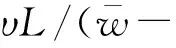
根据式(12)对未知参数向量的估计，在上述控制器设计过程中，需要基于当前时刻已知参数φ1、φ2、…、φj对未来时刻φj+1、φj+2、…、φL的近似估计值进行预报。本文使用一种多层梯度算法[12]来实现待估参数的预报。

首先建立参数预报自回归模型：

(15)

令

式(14)可以简化为

(16)

式中

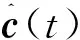
(17)

式中：j=1，2，…，L-1。

综上所述，根据控制律公式(12)、参数估计式(14)及预报算法式(17)可以进行无模型自适应多步预测控制器的设计和应用。

1.4 稳定性和收敛性分析

针对离散时间非线性非仿射系统(1)，当yr(t+1)=yr且yr为一个常数时，存在一个正数λmin>0使得λ>λmin。根据1.1-1.3节设计的无模型自适应多步预测控制方案，有如下性质：

2)输出和输入序列{y(t)}和{u(t)}有界。

下面分两步进行证明。

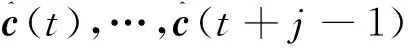
Δc(t)

(18)

由定理1可得|c(t)|≤C，因此Δc(t)≤2C，在式(18)两边取绝对值得式(19)如下：

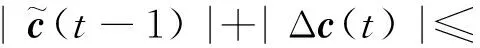
(19)

因为υ>0,μ1>0,μ2>0，且存在常数D，使得

(20)

由此可得：

(21)

步骤2证明无模型自适应多步预测控制系统跟踪误差序列的收敛性以及系统的有界输入输出(bounded input bounded output，BIBO)稳定。

定义系统跟踪误差为e(t+1)=yr-y(t+1)，将式(6)代入误差方程，结合式(12)和式(13)整理可得：

e(t+1)=

(22)

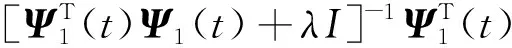
式(22)两端取绝对值：

|e(t+1)|=

(23)

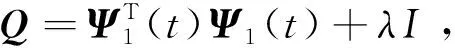
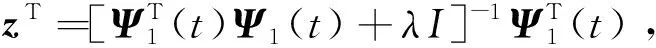
(24)

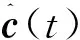
因为Q是一个正定矩阵，det(Q)是λ的首项系数为1的j阶多项式，Q11>0是λ的首项系数为1的(j-1)阶多项式，而其余的Qij(i=2，3，…，j)是λ的首项系数为1的(j-2)阶多项式。故存在λmin>0，使得当λ>λmin时，式(24)的符号与Q11/det(Q)相同。因此存在正常数b使得：

(25)

由式(12)和(13)得：

|e(t+1)|≤b|e(t)|≤…≤bt|e(1)|

(26)

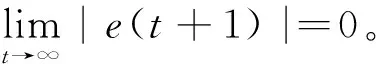
因为yr(t)是有界常数，所以{y(t)}有界。结合式(12) 和式(13)可得：

|Δu(t)|≤

κ|e(t)|

(27)

式中κ是有界常数。

由式(27)推导可得：

|Δu(t)|≤

|Δu(t)|+|Δu(t-1)|+…+|Δu(2)|+|Δu(1)|≤

κ(|e(t)|+|e(t-1)|+…+|e(2)|)+|u(1)|≤

κ(bt|e(1)|+…+b|e(1)|)+|u(1)|≤

κb|e(1)|/(1-b)+|u(1)|

(28)

因此，序列{u(t)}是有界的。

2 直线超声电机建模

电机控制过程中的建模方式包括有限元建模法[13-14]、解析法[15]和等效电路参数辨识法[16-18]。其中，等效电路参数辨识法将直线超声电机的定子、阻尼等器件等效为合适的电子元件，利用机电耦合关系把机械模型等效为电学模型，同时利用成熟的电学理论对超声电机进行工作特性分析。该方法模型结构简单、参数少，是一种研究超声电机控制策略的有效方法。故本文选用等效电路法[19]对直线超声电机的驱动部分和运动部分进行建模分析。

2.1 一维直线超声电机运动平台组成

本文利用实验室直线超声电机平台进行仿真实验。图1为一维直线超声电机系统组成结构。该系统配以LINKS-RT仿真器、一维直线超声电机驱动控制装置、计算机控制模块和上位机，构成一套完整的直线超声电机控制系统开发验证环境。首先利用上位机中Matlab仿真软件对直线超声电机系统进行仿真建模和控制算法编写，编码器生成整个控制算法文件，进行编译后生成可识别代码。可识别代码由RT-Sim仿真器读取并配置，将其通过以太网下载到LINKS-RT仿真器中。LINKS-RT仿真器可以实时监控直线超声电机的运动轨迹以及跟踪误差的变化。计算机运动控制模块将数字信号转换成模拟信号，为直线超声电机驱动控制装置供给输入。光栅传感器和霍尔传感器测量直线超声电机实际位置输出。最后通过一维直线超声电机驱动器控制装置控制电机运动。

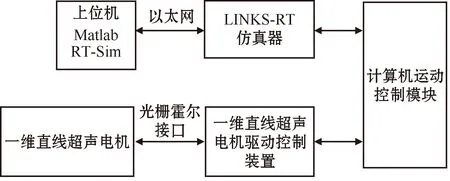
图1 一维直线超声电机系统组成结构

实验室直线超声电机具体性能参数指标如表1所示。本文基于此一维直线超声电机系统进行数学建模和仿真分析研究。

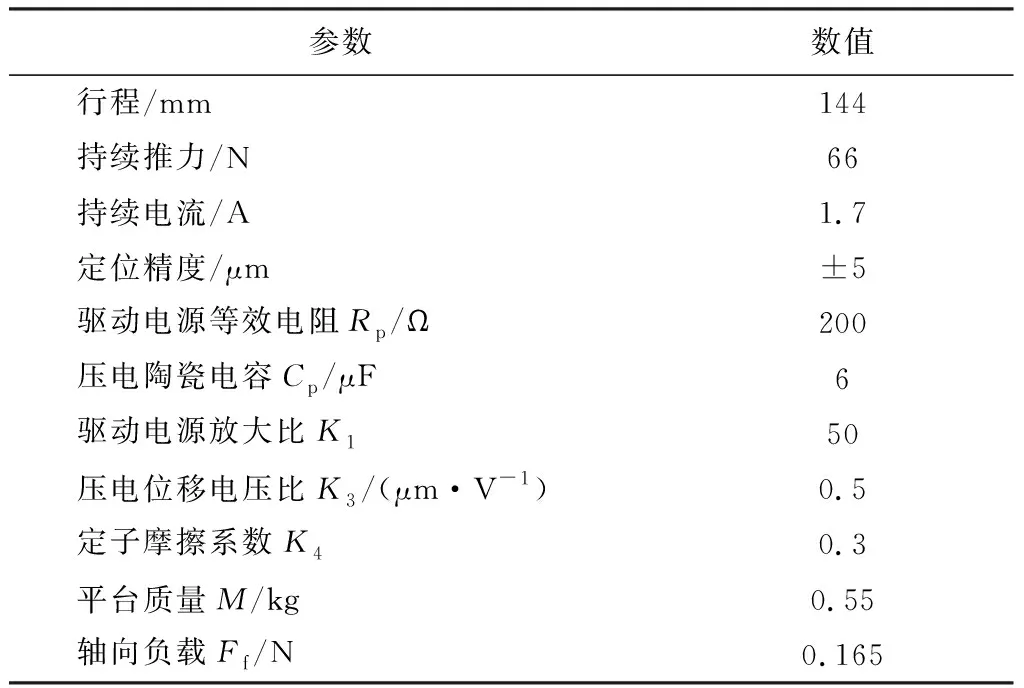
表1 电机相关参数

2.2 直线超声电机驱动部分建模

直线超声电机驱动部分模型如图3所示。

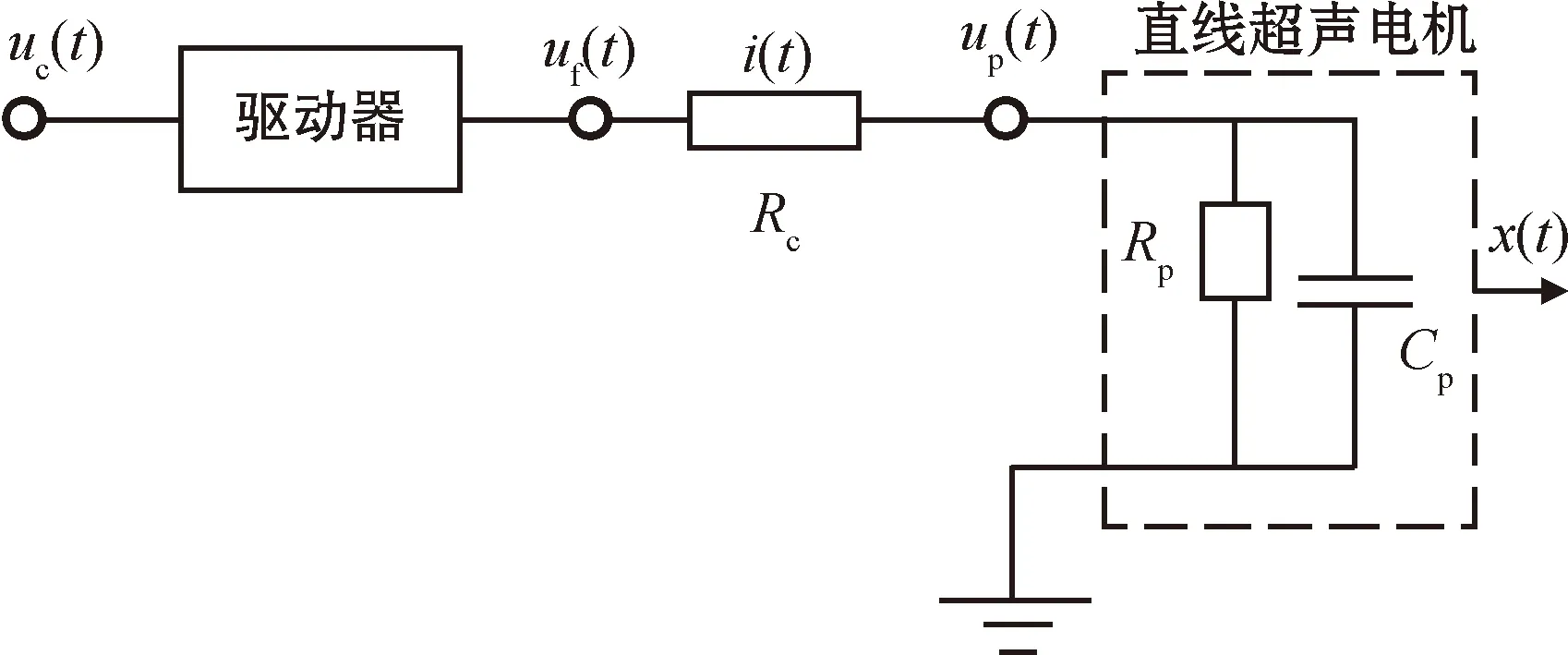
图2 直线超声电机驱动部分建模

因直线超声电机符合电流超前电压的特性，即可视为容性负载[18]，故可将直线超声电机等效为电容来进行后续的建模分析，其中RP、CP为等效电阻和电容；驱动部分uc(t)为控制电压；uf(t)为驱动器放大电压；Rc是驱动器等效电阻；up(t)为施加在直线超声电机上的电压。

本文使用编码型LUSM驱动器进行建模，电压经过驱动器放大，可以看作一个比例环节，比例系数K1=50。该环节传递函数可表示为

(29)

根据图2，由欧姆定律可得

uf(t)=Rc·i(t)+up(t)

(30)

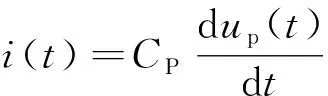
式(30)可简化为

(31)

对式(31)进行拉氏变换，可得

(32)

根据图2，直线超声电机输出位移x(t)和输入电压up(t)可看作比例环节的输出和输入，该环节传递函数如下：

(33)

其中K3为超声电机压电材料输出位移和输入电压的转换比，由表1数据可得，K3=0.5 μm/V。

根据式(29)、(32)、(33)可以得到直线超声电机驱动部分传递函数：

(34)

2.3 直线超声电机运动部分建模

直线超声电机的压电材料的运动和能量转换具有非常明显的非线性，建模非常困难。为了简化建模难度，将直线超声电机运动过程进行简化。因为电机运动平台会受到定子在其运动方向上的推力Ft和垂直于运动方向的位移x(t)，假定这两个量成正比，可得

Ft=K4·x(t)

(35)

式中K4为定子相对平台运动的摩擦系数。

根据简化后的一维直线超声电机的法向接触模型[18]，可得

(36)

式中：M为运动平台质量；Ff为轴向负载。

式(35)代入式(36)并进行拉氏变换，可得

(Ms2+Ff)·V(s)=X(s)·K4

(37)

可以得到运动部分传递函数为

(38)

因为直线超声电机的运动特性，其系统开始运动的瞬时与定子发生振动存在一定的滞后关系，结合驱动部分传递函数式(34)，可以得到整个直线超声电机输入输出传递函数为

(39)

3 仿真研究

3.1 仿真环境及模型参数

基于LUSM-100型直线超声电机运行特性，该系统的输入为电压信号，输出为位置信号。直线超声电机及驱动器的传递函数各项参数如表1所示。通过Simulink仿真软件建立一维直线超声电机的等效电路模型如图3所示。

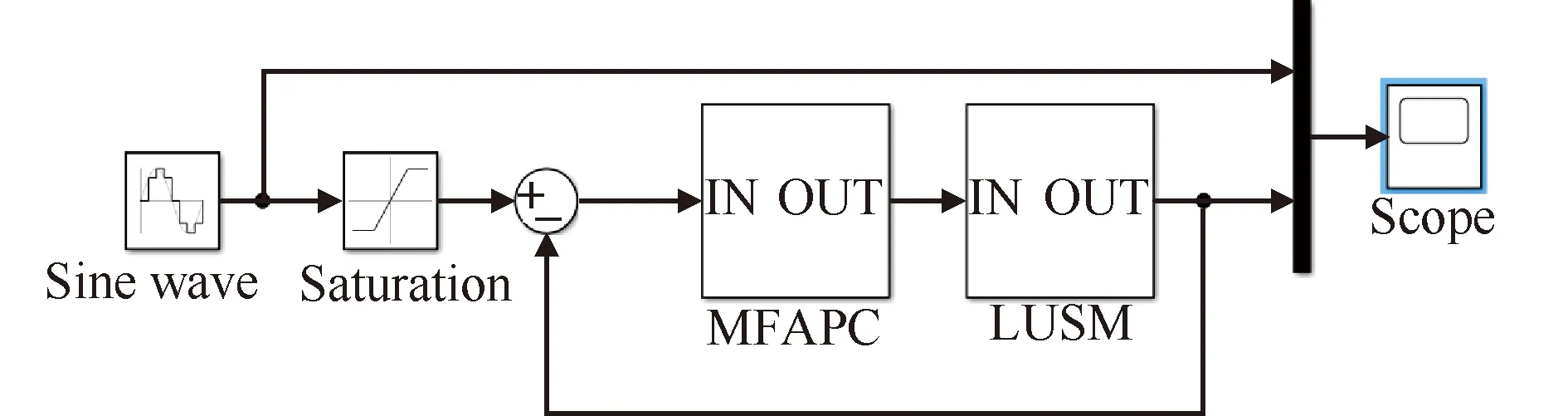
图3 无模型自适应多步预测控制方法仿真

图3中期望跟踪轨线Sine Wave设置成幅值为0.5 mm、频率为1 Hz的正弦信号，模拟直线超声电机位置运动；Saturation模块用于将输入信号限制在设定范围内；MFAPC封装模块为本文所设计的无模型自适应多步预测控制器，内含参数估计、参数预报及多步预测控制等部分。MFAPC控制器的参数依据仿真实验结果进行最优选取，具体如表2所示；LUSM模块为第2节建立的直线超声电机模型；Scope模块为示波器，显示最终仿真结果。

表2 算法参数

3.2 仿真结果

将传统PID算法、无模型自适应单步预测控制和无模型自适应多步预测控制分别应用到一维直线超声电机进行位置控制，并进行仿真结果对比。

PID和无模型自适应单步预测控制的仿真结果如图4所示。

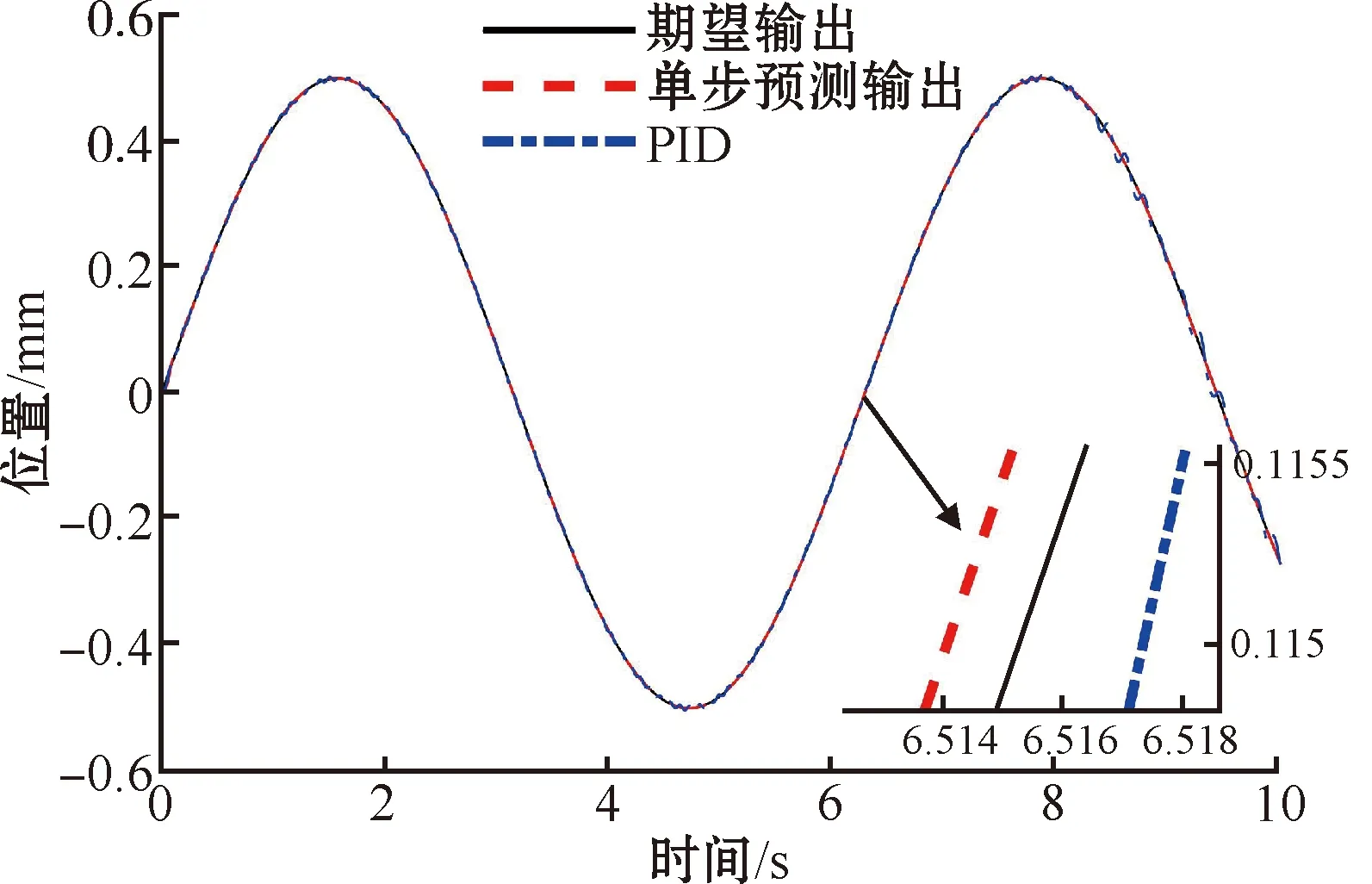
图4 PID和无模型自适应单步预测输出跟踪轨迹

PID和无模型自适应单步预测控制算法的位置误差如图5和图6所示。

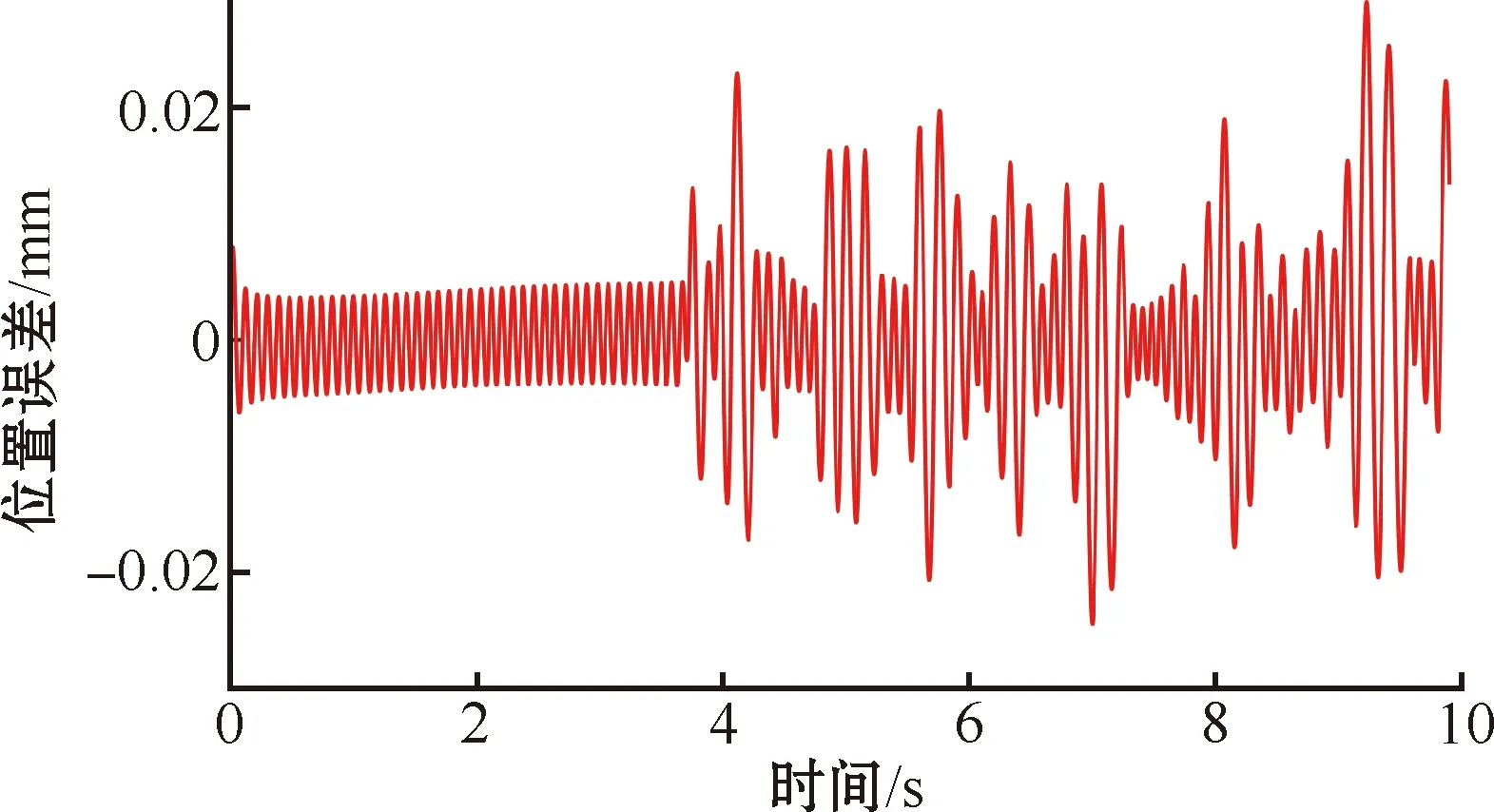
图5 PID跟踪误差

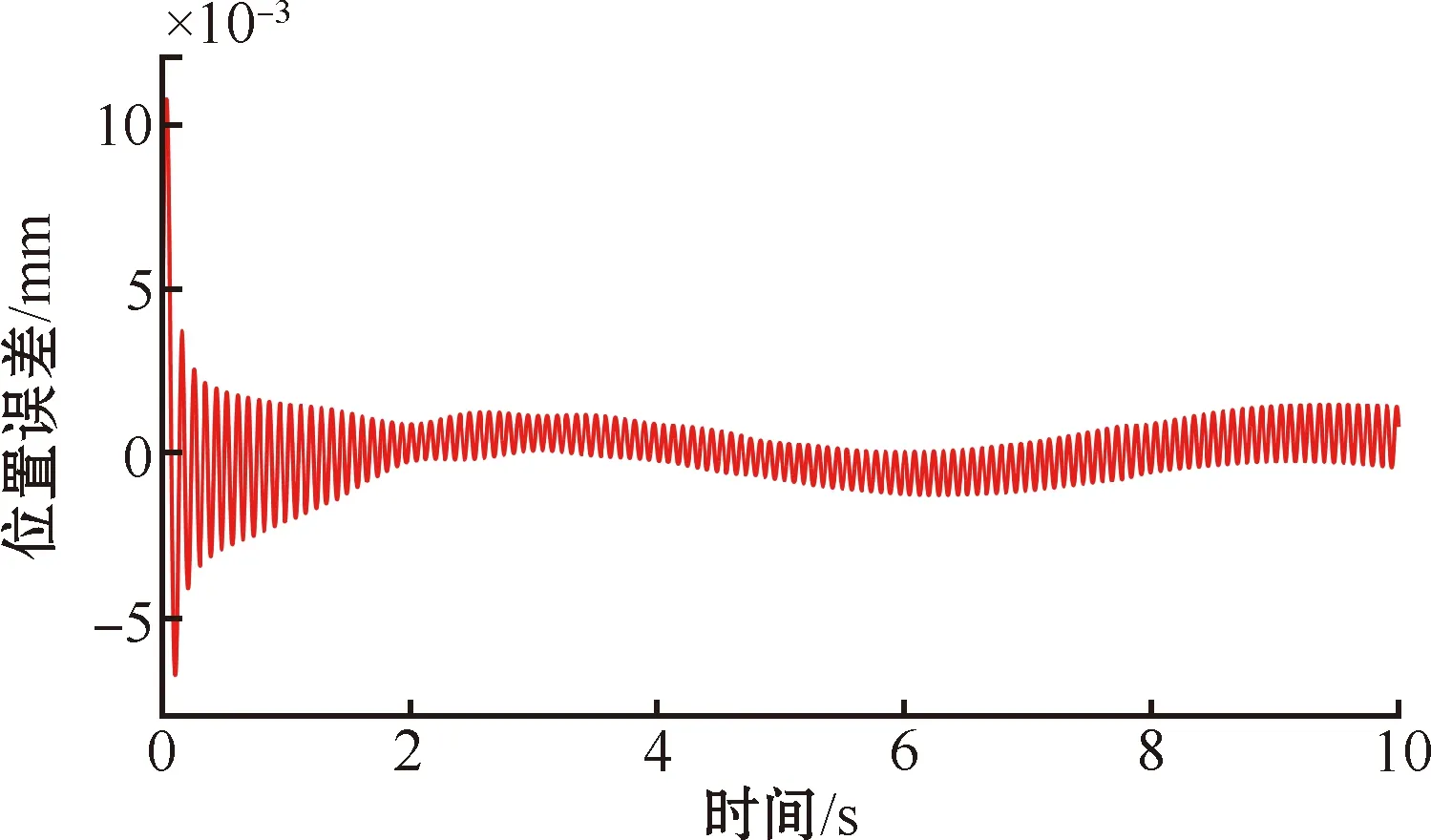
图6 无模型自适应单步预测控制跟踪误差

无模型自适应多步预测控制算法的仿真结果和位置误差如图7和图8所示。

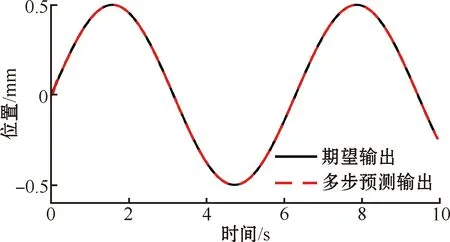
图7 无模型自适应多步预测控制跟踪轨迹

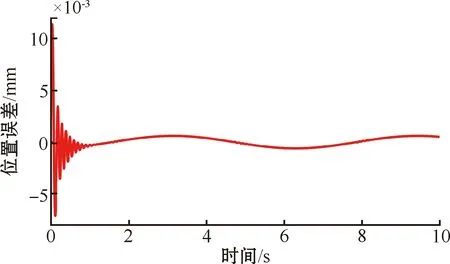
图8 无模型自适应多步预测控制跟踪误差

3种算法在相同条件下的位置误差对比如表3所示。

表3 误差对比 mm

对以上仿真结果分析可知，针对一维直线超声电机这种非线性特征较强的系统时，PID控制器在跟踪性能上不如无模型自适应单步预测控制和无模型自适应多步预测控制，其误差变化较大，实际运行过程中电机会产生抖振，进而严重影响直线超声电机的使用寿命。无模型自适应单步预测控制也存在明显抖振，会对设备使用寿命造成一定影响。而本文提出的无模型自适应多步预测控制算法对直线超声电机的控制误差更小，且误差曲线更加平滑，在直线超声电机系统的实际操作过程中产生的抖振更小。

4 结束语

本文设计实现了基于一维直线超声电机的无模型自适应多步预测控制器，对无模型自适应多步预测控制方法进行了稳定性和收敛性证明分析，该控制器不依赖于直线超声电机系统的精确数学模型，能够及时弥补直线超声电机不确定性及各种扰动对控制性能的影响，从而保证直线超声电机系统能稳定运行且具有较高的控制精度。仿真分析对比了该控制方法和传统的PID控制方法及无模型自适应单步预测控制方法对直线超声电机的位置控制效果，结果表明无模型自适应多步预测控制算法融合了无模型自适应控制和多步预测控制的优点，可有效实现直线超声电机的精确位置控制，进一步减小位置误差，提高跟踪精度，从而提高系统的整体控制性能。