基于深度学习的OFDM系统信道估计方法

陈佳勇，徐湛，职如昕，田露

(北京信息科技大学 信息与通信工程学院，北京 100192)

0 引言

信道估计是正交频分复用(orthogonal frequency division multiplexing,OFDM)系统中非常重要的环节，其目的是估计出信道的时域冲激或者频率响应，在此基础上对接收数据进行校正，以准确地恢复出发送信号。传统的信道估计准则有最小二乘 (least square,LS)[1]、最小均方误差 (minimum mean square error,MMSE)[2]和最小线性均方误差(linear minimum mean square error,LMMSE)[3]。LS估计算法不需要先验信息，计算量小且易于实现，但是由于忽略了接收信号中的噪声，其估计精度将随着噪声的增大而降低。MMSE估计算法考虑了信道的统计特性，需要对信道自相关矩阵求逆，计算量较大。LMMSE算法在MMSE算法上进行了改进，虽然减少了一定的计算量，但同时也降低了一定的计算精度。

将深度学习应用于信道估计是近些年的研究热点。文献[4]把无线信道和OFDM系统看作黑盒子，离线训练深度学习模型，用于恢复在线传输的数据。文献[5]与文献[4]的不同之处在于根据计算模型输出误差得到的差异度值对前向反馈(back propagation,BP)神经网络进行集成，通过使用集成神经网络模型进行信道估计。文献[6]则对信道响应进行估计，提出了一种在线训练数据的模型结构，训练过程更快，所需的训练数据大大减少。为了更好地消除噪声对信道估计的影响，文献[7]采用了一种特殊设计的基于深度图像先验的深度神经网络(deep neural network，DNN)，先对接收信号进行去噪，然后进行传统的LS估计。文献[8]提出了一个用于多进多出(multiple input multiple output,MIMO)系统信道估计的深度学习网络，通过展开迭代算法优化训练参数，进一步提高了信道估计的性能。

一般基于DNN的信道估计模型是在全信噪比下进行训练，这样会导致神经网络对低信噪比下的信道响应估计的拟合程度较差。本文提出了对低信噪比区间和高信噪比区间的OFDM接收信号分别进行离线训练的信道估计策略，以提高算法对于不同信噪比条件的适应性。利用每帧OFDM信号的前导符号对当前OFDM符号进行信噪比估计，根据其结果选取相应的DNN模型进行在线信道估计。

1 OFDM系统模型

OFDM系统分为发射机与接收机两部分。在发射端，数据进行循环冗余校验(cyclic redundancy check，CRC)，信道编码，打孔，交织，星座映射，插入导频并进行子载波加扰后进行反向傅里叶变换(inverse fast Fourier transform,IFFT)，然后加入循环前缀(cyclic prefix,CP)形成OFDM符号进行传输。接收端则为发射端的逆过程，在去除CP之后进行快速傅里叶变换(fast Fourier transform，FFT)，经过信道估计环节对其进行均衡、解调等操作后就可以恢复出发送的数据。

OFDM信号在经过多径信道以及噪声干扰后，接收端信号的频域形式可以表示为

Y(k)=H(k)X(k)+Nw(k)

k=0,1，…，N-1

(1)

式中：N为一个OFDM符号的子载波数目；k为子载波序号。H(k)为第k个频点上的信道响应；X(k)为发送的符号；Nw(k)为加性高斯白噪声(additive white Gaussian noise，AWGN)。

为了获取信道的准确信息，需要对其进行估计，传统的LS估计方法是借助于导频实现的，可表示为

(2)

式中：Yp和Xp分别为接收端和发送端的导频符号，符号长度为导频子载波个数Np。

2 基于深度学习的信道估计

2.1 DNN模型基本结构

本文使用的神经网络模型由输入层、3层隐藏层和输出层组成。各层神经元的数量分别为32，30，60，120，224。本文采用的OFDM子载波数为128，其中导频子载波数为16，数据子载波数为112。由于需要将复数的实部和虚部拆分开，因此将神经网络的输入层神经元数设为32，输出层神经元数设为224，隐藏层神经元数逐层增加来增强DNN非线性拟合的能力。DNN信道估计算法的基本学习过程由信号的正向传播与误差的反向传播两个过程组成。

(3)

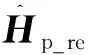
然后通过式(4)得到第一隐藏层的输入向量u(1)：

u(1)=W(1)x+b(1)

(4)

式中：u(1)为n1维行向量，n1为第一隐藏层神经元个数；n1×2Np矩阵W(1)为输入层与第一隐藏层之间的权重矩阵；b(1)为n1维偏置向量。

接着在非线性激活函数的作用下，得到第一隐藏层的输出向量x(1)：

x(1)=f(u(1))

(5)

式中，激活函数f(·)为Sigmoid函数，可以表示为

(6)

同理可以得到整个神经网络模型的输出向量为

y=f(W(l-1)(…f(W(1)x+b(1))…)+b(l-1))

(7)

式中：l为神经网络的层数；y为2Nd维行向量，Nd为一个OFDM符号中数据子载波的数目。

将输出层输出的结果重新组合成复数的形式便可以得到由神经网络预测的数据符号处的频率响应。

由于信道频率响应的值是有正负的，而Sigmoid函数的输出范围为[0,1]，所以输出层的激活函数选择Tanh函数，其输出范围为[-1,1],可表示为

(8)

反向传播时，以一个3层的神经网络为例，将损失函数表示为

(9)

式中：m为输出层神经元数目；yj为输出层第j个神经元的值；zj为对应的输出层标签值。

每次需要调整的权重值可以表示为

(10)

式中：wij为第i个隐藏层神经元与第j个输出层神经元之间的权重值；η为神经网络的学习率。

由链式法则，可以将式(10)改写为

(11)

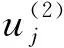
同理可以得到偏置项更新的表达式为

(12)

隐藏层和输入层之间权重与偏置项的更新方式同上。每次迭代按照梯度下降算法更新权重与偏置项的值，直到达到设定的迭代次数。

2.2 基于前导符号的信噪比估计

本文在每帧OFDM符号前增加一个前导符号用来粗略地估计出当前帧OFDM符号的信噪比。整个OFDM帧结构如图1所示，其中，前导符号为经过正交相移键控(quadrature phase shift keying,QPSK)调制的导频符号。后续每个OFDM符号的导频图案为梳状导频，即在频域上等间隔地插入导频，有利于克服快时变衰落信道对信道估计的影响。

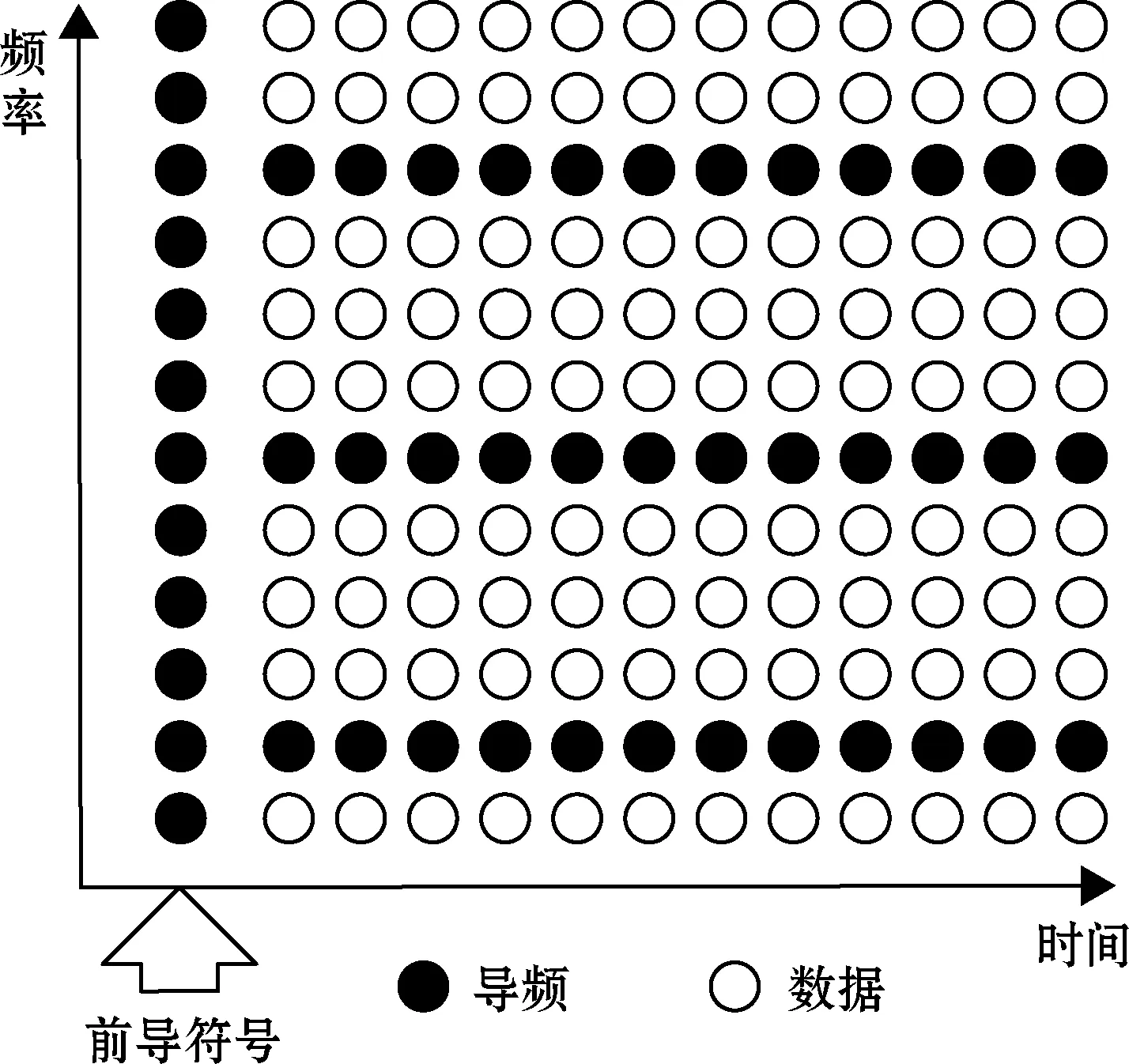
图1 带有前导符号的OFDM帧结构

n=0,1,…,N-1

(13)

式中，n为时域冲激响应的序号。

然后通过式(14)得到各点的能量：

(14)

式中，conj(·)表示取共轭。

接着使用一个长度为循环前缀大小的滑窗对时域冲激响应进行搜索，得到信号能量最集中的区域，同时对时域总能量进行计算：

(15)

Emax=max{E}

(16)

(17)

式中：m为滑窗能量的序号；Ncp为循环前缀的长度；Emax为滑窗能量的最大值；Eall为时域总能量。

最后通过式(18)～(20)可以计算出噪声的平均功率PN、信号的平均功率PS以及当前OFDM符号的信噪比Rsn：

(18)

(19)

(20)

2.3 基于信噪比预测的DNN信道估计

基于信噪比预测的DNN信道估计算法由训练和估计两部分组成。

(21)

式中：y(j)为输出层第j个神经元的值；z(j)为Hd的实部和虚部组成的标签向量的第j个值，z=[Hd_reT,Hd_imT]T，为2Nd维列向量。

本文中神经网络的所有参数采用高斯分布进行初始化，训练过程的学习率设置为0.5，梯度下降算法选用的是小批量梯度下降，从训练数据集中每次选取1 000个样本对参数进行更新，训练的迭代次数设置为200。

训练完成后的模型即可用来进行信道响应的在线估计，过程如图2所示。

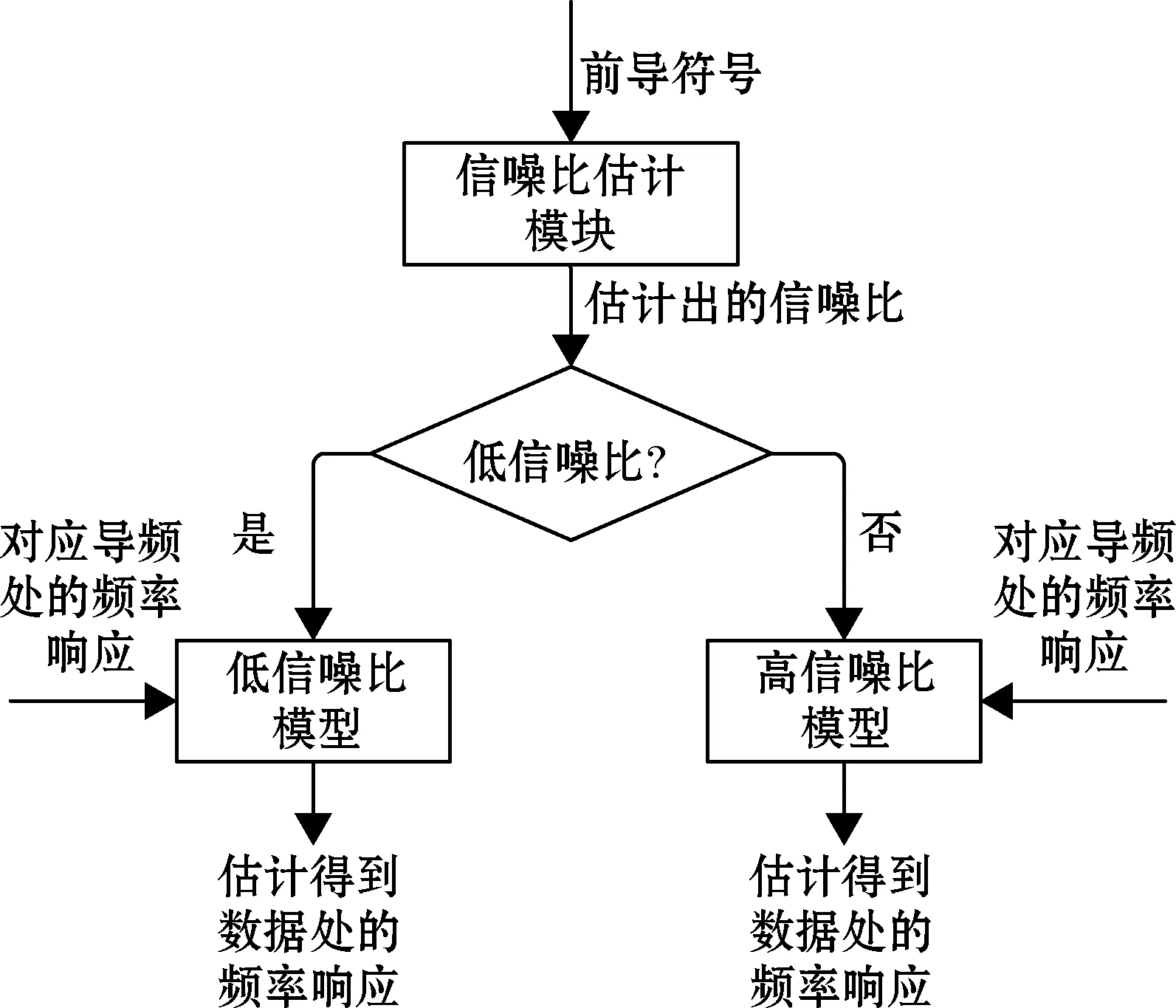
图2 基于信噪比预测的信道估计流程

3 仿真结果

本文提出的方法实际上相当于在LS估计后进行频域插值，所以将本文方法与传统线性插值和离散傅里叶变换(discrete Fourier transform,DFT)插值进行比较。此外，本文设置的低信噪比区间为0～10 dB，高信噪比区间为10～20 dB。比较的性能指标为信道响应的均方误差(mean square error,MSE)和系统误码率(bit error ratio,BER)。训练集和测试集均由在Matlab上搭建的如图1所示的OFDM系统产生，发送数据经过无线信道并且叠加上加性高斯白噪声后由接收机接收并进行信道估计处理。在0～20 dB的区间上每1 dB产生20 000帧OFDM符号的数据。

仿真实验参数如表1所示。

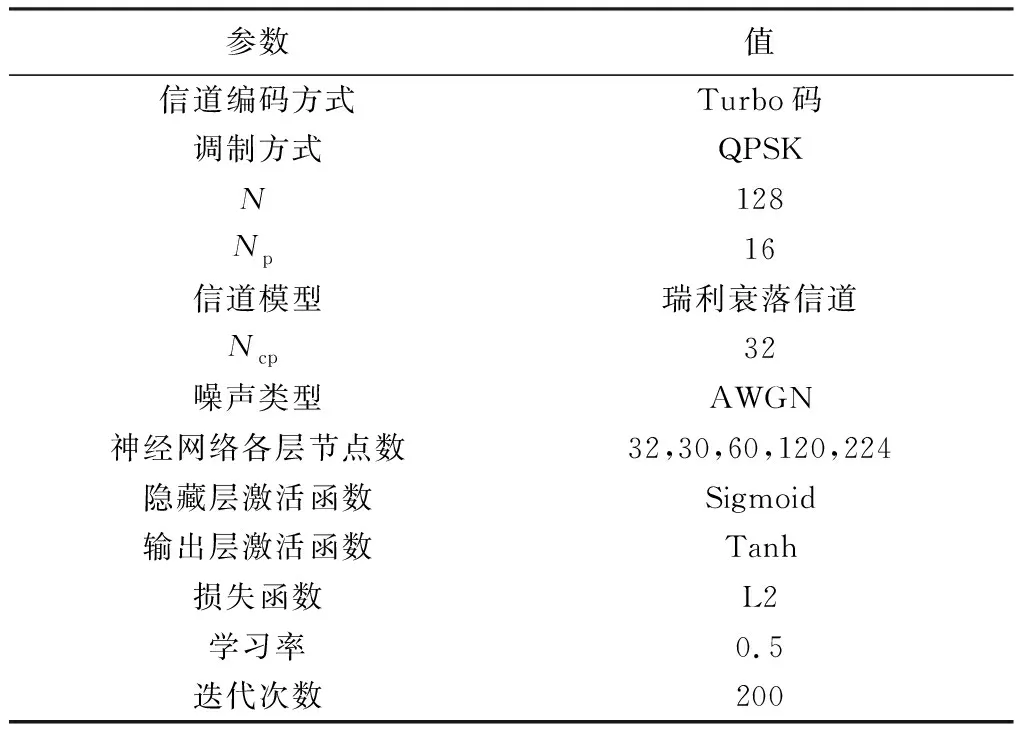
表1 仿真参数设置

不同信道估计方法的MSE性能如图3所示。由图3可以看出，线性插值虽然实现简单，但是当导频间隔较大时(本文实验设置的导频间隔为8)，线性插值便不能有效地描绘出导频间信道响应的变化，因此在估计信道响应时表现较差。而DFT插值在时域上有去噪的操作，因此对信道的估计效果较线性插值有所提升。DNN模型通过将导频处的信道信息进行非线性映射得到整个OFDM符号完整的信道信息，其信道响应均方误差比DFT插值有一定的性能提升。而本文提出的基于信噪比估计的DNN(SNR-DNN)方法，由于将训练时的信噪比划分为低信噪比区间和高信噪比区间，处于低信噪比区间时能够有效地学习噪声对信道状态的影响，在高信噪比区间时可以加强DNN模型对信道状态自身变化的学习。当MSE为10-2时，SNR-DNN比在全信噪比区间训练下的DNN模型所需的信噪比要低3 dB左右。

图3 不同信道估计方法的MSE性能

不同信道估计方法的BER性能如图4所示。由图4可知，线性插值由于不能很好地描述信道信息，系统误码率最高。DFT插值比线性插值的BER性能已经有显著的提升，但由于无法对CP范围内的噪声进行有效处理，其性能仍低于DNN信道估计。而本文提出的SNR-DNN方法可以分别对低信噪比和高信噪比区间下的信道状态进行有效学习，因此当BER达到10-3时，SNR-DNN比DFT插值所需的信噪比要低4 dB左右；当BER达到10-4时，SNR-DNN比DNN模型所需的信噪比要低2 dB左右，并且与理想估计的结果也较为接近。

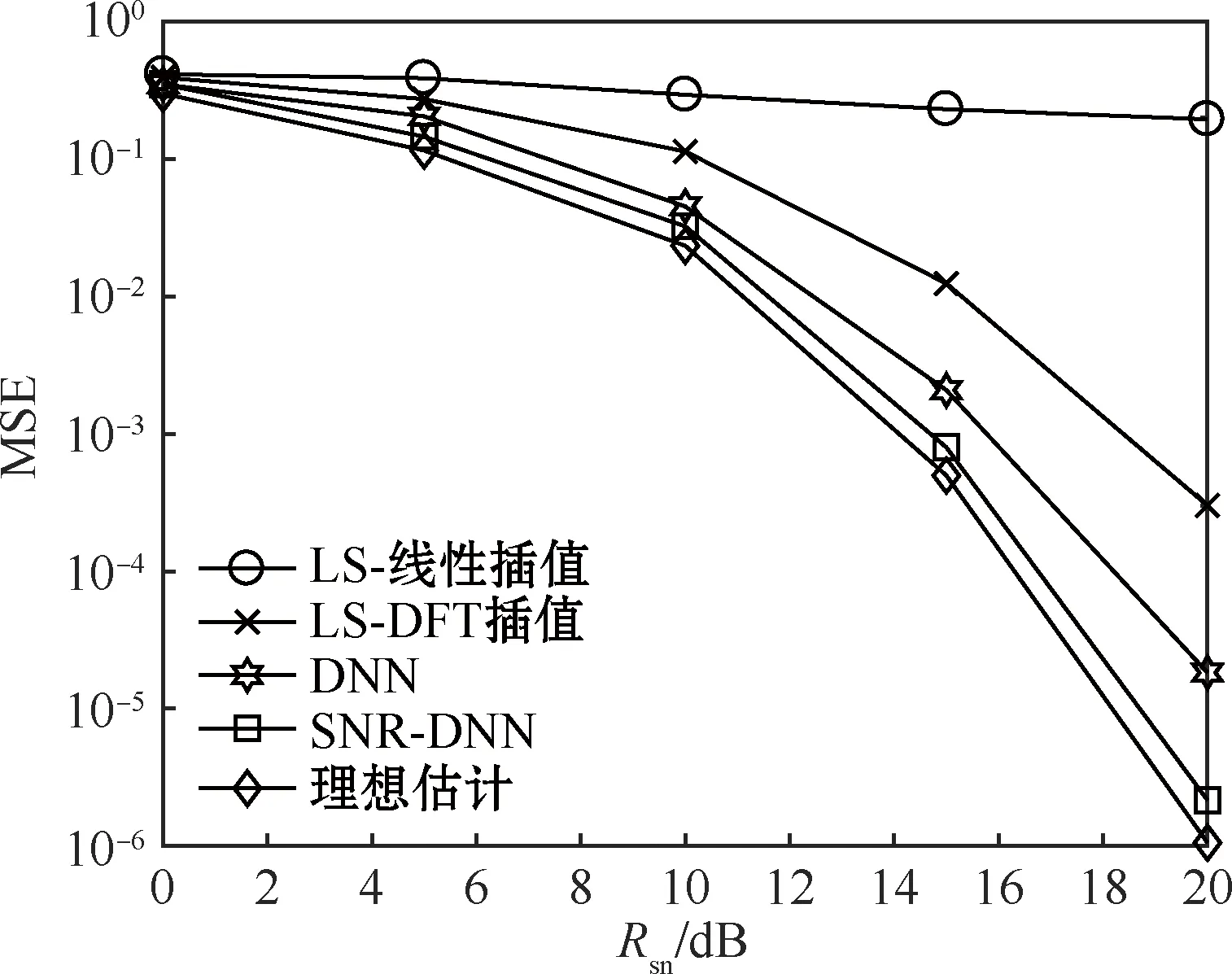
图5 不同信道估计方法的BER性能

表2对比了线性插值、DFT插值以及SNR-DNN的时间复杂度。其中，线性插值的时间复杂度最低，DFT插值由于涉及傅里叶变换，时间复杂度较高。而SNR-DNN算法每层仅进行乘法和加法的运算，因此，复杂度和线性插值在同一个数量级。

表2 时间复杂度比较

4 结束语

为了提升传统的DNN信道估计方法的性能，对高低信噪比区间下的OFDM符号进行训练，加强了低信噪比时DNN模型学习噪声影响信道状态的能力，同时在高信噪比时可以使DNN模型更有效地学习信道自身状态的变化。在线估计时，利用前导符号可以预估出当前OFDM符号的信噪比，从而选择相应区间的模型进行估计，提升了信道估计的性能。