汽车传动轴振动的仿真分析与优化
王成明,张得富,陈云升
(1.郑州大学机械与动力工程学院,河南 郑州 450001;2.许昌远东传动轴股份有限公司,河南 许昌 461111)
1 引言
随着我国汽车保有量的逐年增加,道路条件的改善以及人们环保意识的不断加强,汽车的舒适度越来越受到大众的关注。汽车传动轴作为汽车动力传递的重要零部件,在高速旋转的状态下,所造成的过大的振动、异响等都直接影响汽车传动轴部件本身以及其他关联零部件的寿命[1-2],同时严重影响乘客以及行人的身心健康。
某汽车传动轴生产商采集的装配该型号传动轴乘用车的反馈中指出,在(90~100)km/h的行驶速度下,乘客明显感受到振动加剧,经分析判断主要原因是汽车传动轴工作频率与固有频率接近,导致了共振。该型号乘用车因其轴距大,故采用2根传动轴连接的方式,其中间支撑结构复杂、动态性能难以确定,这些因素制约着共振问题的解决。
长期以来,该公司采用传统的测试方法,该方法只能针对已加工装配完成的样品,不能用于研发设计阶段,而采用CAE方法进行模态分析具有方便更改设计方案、周期短、成本低等优点,因此,传统生产模式亟需改变[3-4]。
这里应用Ansys有限元软件对该型号乘用车传动轴总成进行模态分析,并通过仿真分析方法的改进,建立更加准确的汽车传动轴总成模型;应用Adams 建立虚拟样机模型进行动力学仿真,得出精确的影响规律,为传动轴总成的设计、中间支撑性能的确定、该型号乘用车减振降噪提供依据。
2 汽车传动轴总成自由模态分析
2.1 传动轴有限元模态分析
该乘用车传动轴主要由滑动叉、前后轴管,中间支撑总成、十字轴万向节总成、突元叉等零部件组成,如图1所示。
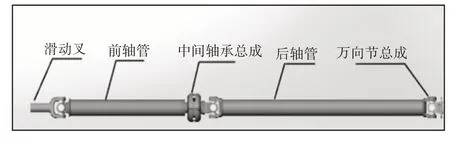
图1 传动轴总成结构图Fig.1 Transmission Shaft Assembly Structure
所建传动轴总成仿真模型尽量还原传动轴实际结构特征以及各个零部件之间的连接方式,如轴承和轴头,万向节总成等装配关系利用刚性单元模拟,并放开相应转动自由度,保证有限元分析结果的准确性[5]。
前后轴管采用45#钢,轴头、万向节总成、突元叉等采用40Cr,中间支撑采用天然橡胶,按实际情况定义各部分零部件材料,确保准确的物理特征及质量分布[6]。前后传动轴管,轴头部分等采用六面体实体单元,其余零部件采用四面体网格划分,最终建立的节点单元为280816,模型单元数为126330。
由于传动轴低阶模态对该系统振动影响较大,高阶模态影响较小,求解出其前4阶自由模态,频率及振型,如图2、表1所示。
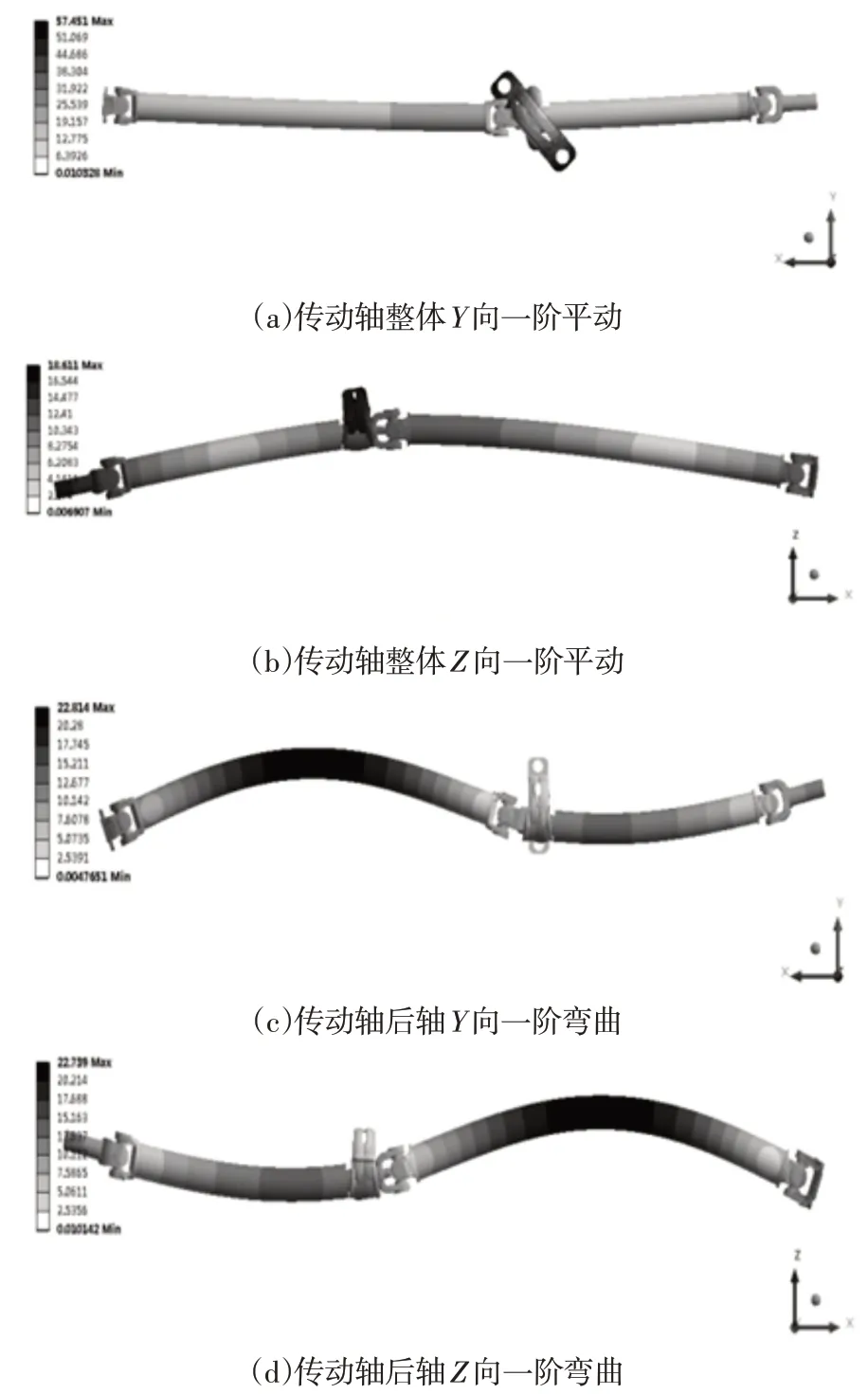
图2 自由模态仿真振型图Fig.2 Vibration Mode Graphics of Free Modal Simulation

表1 仿真分析结果Tab.1 Simulation Analysis Results
2.2 自由模态实验分析
实验测试采用比利时LMS 公司的Test.lab 模态分析系统、SIEMENS 40通道数据采集前端以及PCB模态传感器等。测试方法采用锤击实验法,两端以及中间支撑处采用尼龙绳悬挂,将该型号传动轴14等分即15个等分点,三个三方向加速度传感器分别贴装在敲击点2,7,13处布置,如图3所示。以轴向为X向,采用力锤对(1~15)均匀分布点的+Y,+Z向分别敲击5次,采集记录模态数据。求解出其前4阶模态,频率及振型,如图4所示。

图3 实验布置图Fig.3 Experimental Layout
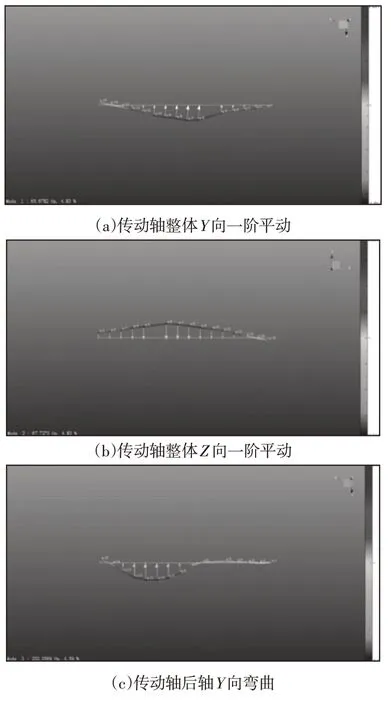

图4 自由模态实验振型图Fig.4 Vibration Mode Graphics of Free Modal Experiment
2.3 结果分析
将仿真分析结果与实验测试结果对比,如表2所示。可见各阶次振型以及频率基本一致,数值相近,平均相对误差为3.58%,说明建立的仿真模型基本满足要求,具有一定的实用价值。
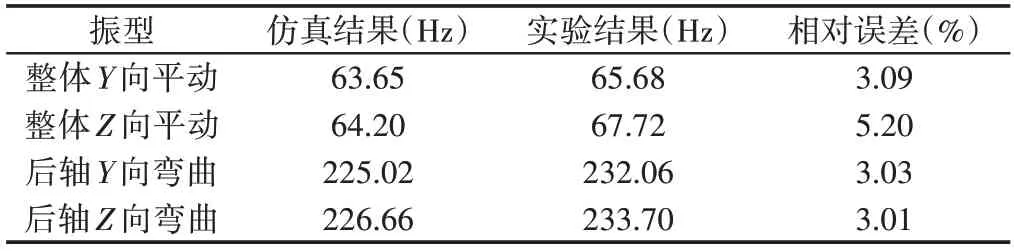
表2 仿真与实验结果对比Tab.2 Comparison Between Simulation and Experimental Results
3 模型修正及分析
3.1 中间支撑总成性能试验分析
由于中间支撑橡胶外形结构的复杂性,以及弹性模量的时变特性,使形状不规则的中间支撑结构很难通过解析公式预测其刚度[7],往往通过经验取值进行仿真计算,导致该传动轴总成的固有频率、振型产生较大误差,对分析结果造成一定影响,延长传动轴设计优化的周期。传动轴的振动通过中间支撑传递给底盘,影响汽车的舒适性,而轴向窜动影响较小,所以决定利用垂向和横向弹簧连接替代中间支撑总成结构。随机抽样三个该型号中间支撑总成试件进行动静态特性台架实验,以确定该型号中间支撑总成的实际刚度,实验台架及安装方式,如图5所示。

图5 中间支撑动态性能实验Fig.5 Dynamic Performance Experiment of Intermediate Support
根据中华人民共和国铁道行业标准TB/T2843-2007《机车车辆用橡胶弹性元件通用技术条件》[8]中的静态性能试验方法,实验采用正反两方向加载卸载方式,对试件从零加载到实验载荷上限,以加载速度卸载到零,反向加载到载荷下限,以相同速度卸载到零;第三次开始记录载荷—变形曲线,如图6所示。
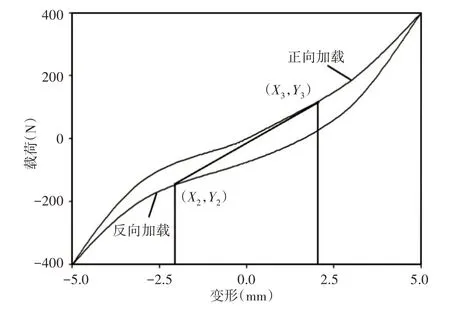
图6 正反方向加载卸载、载荷-变形曲线Fig.6 Load-Deformation Curve Under Loading and Unloading in Both Directions
刚度K计算公式:

式中:Y1、Y2—载荷,单位(N);X1、X2—变形,单位(mm)。
实验结果,如表3所示。
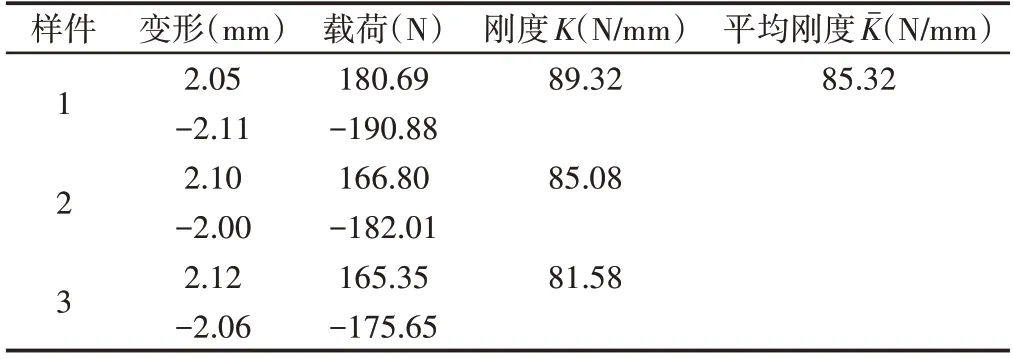
表3 刚度实验结果Tab.3 Results of Stiffness Experiment
3.2 修正模型模态分析
根据传动轴的实际安装形式,以此约束传动轴输入端滑动叉和输出端突元叉的六个自由度,弹簧单元一端固定轴承位置,一端固定于地面,如图7所示。设置弹簧刚度为85N/mm,其它约束条件和装配关系与自由模态分析一致。通过修正模型并进行约束模态分析求解,结果及振型,如表4所示。
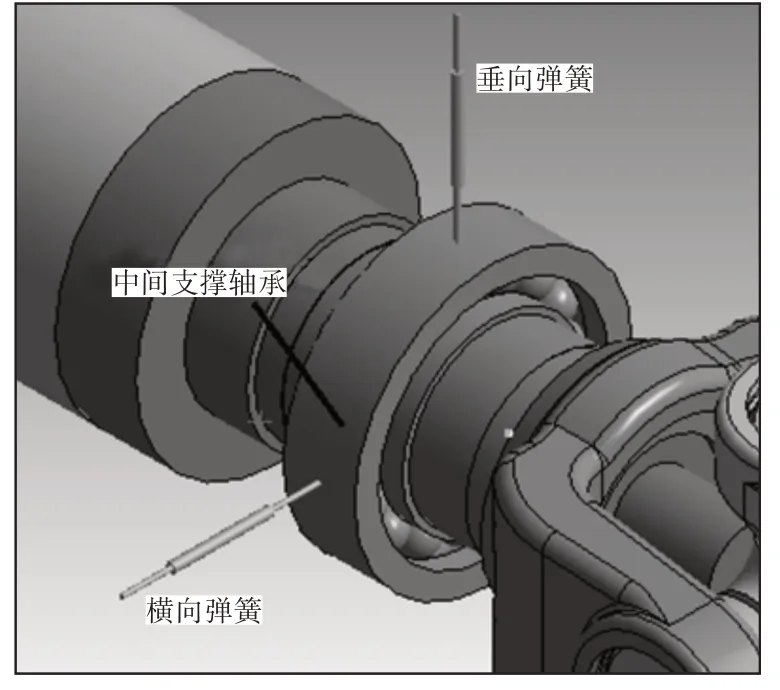
图7 弹簧连接模型Fig.7 Spring Connection Model

表4 约束模态仿真结果Tab.4 Constrained Modal Simulation Results
3.3 结果分析
采用相同刚度的弹簧替换原来传动轴总成中间支撑部件,并添加符合实际工况下的边界约束,得到准确的仿真结果以及振型图。由模态分析可知,传动轴整体一阶平动模态对应频率大致为68Hz左右,传动轴一阶弯曲模态对应频率大致为255Hz左右。根据振动理论可知,当激振频率与固有频率接近时会引起共振,发生异响,噪音增大,影响整车的安全性[9]。根据该车型的配置参数:发动机最高转速5600r/min,最高档减速比i1为0.778,车轮半径0.316m,主减速比i为4.778。通过计算可知,一阶平动模态频率对应车速101.67km/h,与实际客户反映的问题具有一致性,并且验证了修正模型的正确性和分析结果的正确性。而一阶弯曲模态对应的时速为381.28km/h,远远超出最高车速,不予考虑。传动轴在设计阶段,轴管长度、厚度、中间支撑的位置等都已经确定,不能通过优化设计该影响因素达到减振的目的,因此合理设计中间支撑的刚度是解决该问题的有效措施。
3.4 临界转速与安全系数
传动轴临界转速nk计算方法与安全系数K通过以下公式计算[10]:
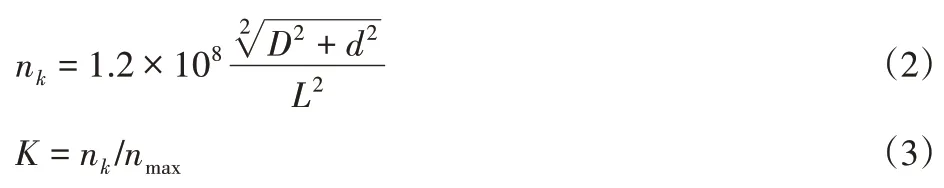
式中:D、d—轴管外、内径(63.5mm、60.3mm);L—两万向节中心距离(后轴为865mm);nmax—传动轴最大转速;nmax=nemax/i1,nemax—发动机最高转速;i1—最高档减速比。根据上述参数计算得临界转速nk=14044r/min,K=1.95>1.2,即满足稳定性要求。
该传动轴采用两节传动轴连接的方式,只理论校核较长的后轴存在一定的局限性,需要进行台架实验以验证传动轴总成的稳定性。安装方式,如图8所示。实验参照QC/T523-1999《汽车传动轴总成台架试验方法》[10],随机选取3件该型号传动轴样品,编号1#、2#、3#,激振发生器位于后轴中点,扫频范围取(0.5~1.2)nk对应的频率范围,即(117~280)Hz,扫频步进为1Hz/s,如图9、表5所示。

图8 临界转速实验布置图Fig.8 Critical Speed Test Layout
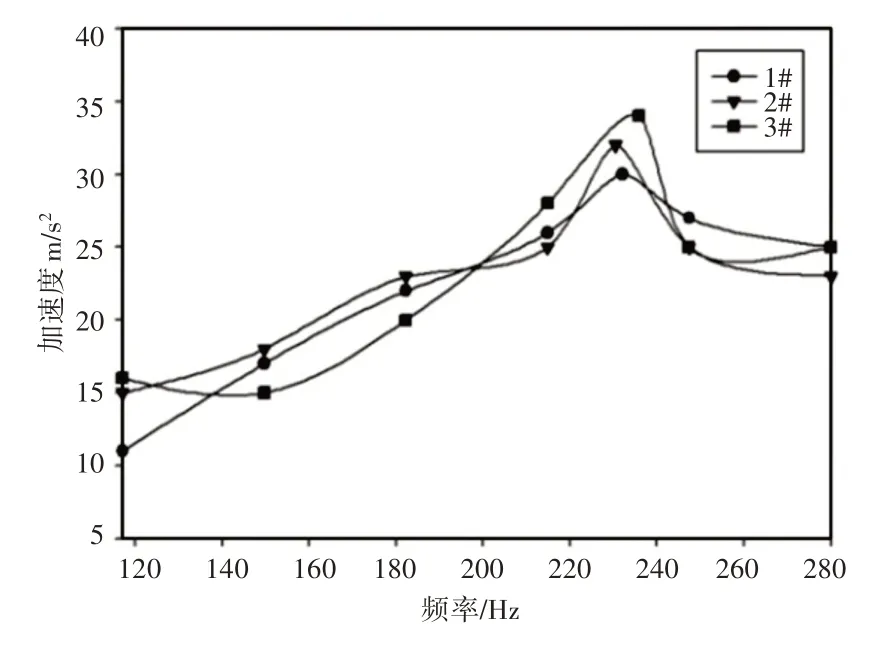
图9 临界转速实验扫频图Fig.9 Sweep Frequency Figures of Critical Speed Test
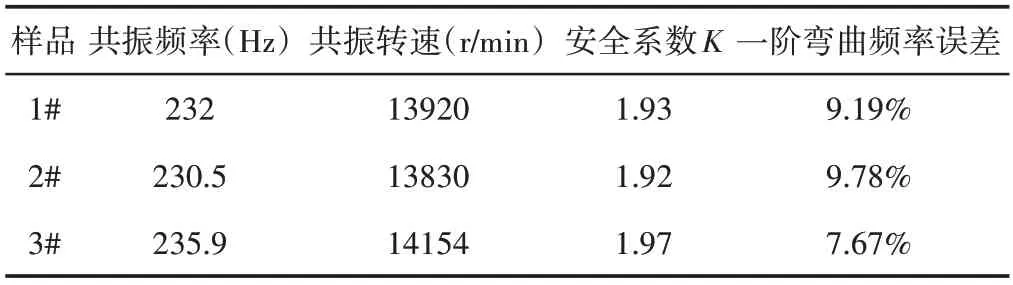
表5 临界转速实验结果分析Tab.5 Analysis of Critical Speed Test Results
分析可知,随机选取的传动轴样品共振频率即为一阶弯曲频率,由于实验台架与激振设备的存在,与仿真分析约束条件存在一定的误差,且最大不超过10%,验证了仿真模型的正确性。同时计算安全系数均大于1.2,满足稳定性要求,不会发生弯曲断裂的情况。
4 中间支撑刚度优化设计
4.1 中间支撑刚度理论计算
根据系统隔振理论可知,隔振效果的好坏取决于振动传递率TA的大小。TA越小,表明通过隔振系统传递的力或者运动越小,隔振效果越好。TA的大小取决于系统的刚度K、阻尼系数C、阻尼比ξ的大小。无论阻尼比ξ取何值,当频率比λ=ω/ωn>时,TA值小于1,隔振系统能起到真正的作用[7]。其中ω为激振频率,是传动轴转动产生的,即轴转动频率;ωn为中间支撑固有频率。由于在车速为(90~100)km/h产生剧烈振动,因此取范围内平均车速v=95km/h=1583.3m/min计算,n=vi/2πr=3812.17r/min。
激励频率与中间支撑固有频率之比:

中间支撑固有频率:

中间支撑的刚度为:

式中:ω=2πn/60=399.06rad/s;m—中间支撑的支撑重量,传动轴前轴5.5kg,后轴6.7kg,支撑重量m可认为是总重一半即m=6.1kg。
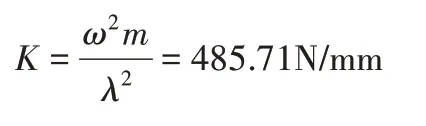
所以为了满足系统隔振要求,在设计阶段,中间支撑的径向刚度应小于485.71N/mm。
4.2 中间支撑刚度参数优化设计
应用Adams仿真软件对传动轴建立虚拟模型,依据实际装配条件对各个零件进行约束,万向节总成建立胡克副,前后轴管与万向节部分建立固定副,中间支撑以弹簧连接模拟,轴承与轴建立转动副,滑动叉与突元叉与地面建立转动副,在滑动叉(输出轴)建立驱动,突元叉(输出轴)输入恒定的反扭矩模拟阻力矩,同时根据实际的安装工况,调整后轴安装角度为4°,从而建立实际的传动轴动力学仿真模型,如图10所示。
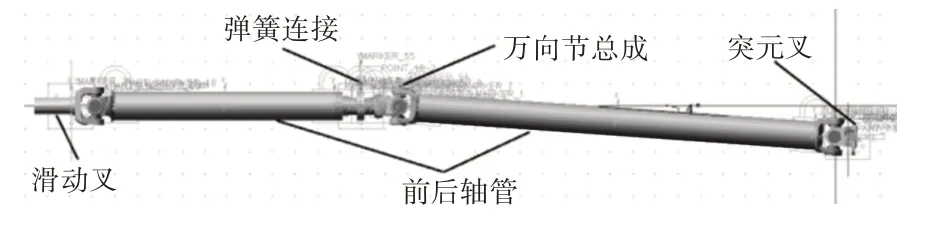
图10 运动学仿真模型Fig.10 Dynamics Simulation Model
以中间支撑弹簧刚度为设计变量,刚度约束(0~1000)N/mm;以中间支撑轴承质心垂直方向加速度绝对值最大值为目标函数;约束函数是保证传动轴真实的工况下运转,即所添加的约束、负载、驱动、弹簧等条件。设置转速分别为1000r/min、2000r/min、3000r/min、4000r/min探究不同转速下刚度对加速度的影响规律,全面反映刚度参数优化的合理性结果,如图11所示。
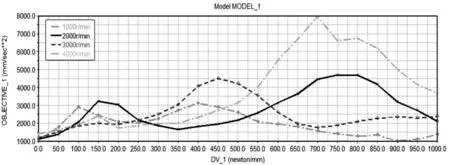
图11 不同转速下刚度参数优化设计Fig.11 Optimization Design of Stiffness Parameters at Different Speeds
由图11 分析可知,在(0~75)N/mm 和(225~325)N/mm 范围内,各个转速下的目标值均较小。但刚度值过小会造成弹性元件难以支撑传动轴总成的重量,引起稳定性等问题。因此,综合中间支撑刚度值理论优化结果,刚度值应选择(225~325)N/mm 较为合适,尤其刚度在275N/mm 附近时,对于不同转速,其加速度均较小。
4.3 优化后结果分析
采用刚度优化到275N/mm,对车速95km/h即传动轴转速为3812.17r/min工况下,刚度优化前后中间支撑轴承加速度和振幅效果图,如图12所示。
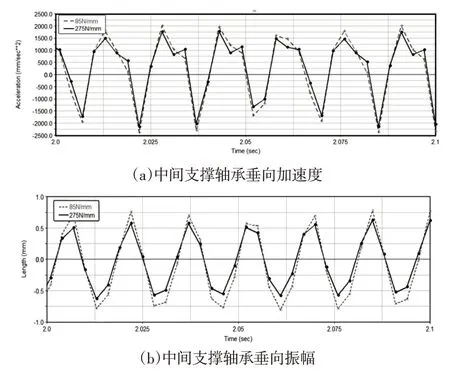
图12 优化前后加速度和振幅效果图Fig.12 The Effects of Acceleration and Amplitude Before and After Optimization
由图12可知,刚度在85N/mm和275N/mm时加速度绝对值最大值分别为2293.28 mm/s2、2159.72mm/s2,降幅为5.82%;刚度在85N/mm和275N/mm时下振幅最大值分别为0.82mm、0.63mm,降幅为23.17%,因此该中间支撑刚度的优化方案有效,起到明显的减振效果。
5 结论
(1)通过Workbench 对某型号汽车传动轴总成自由模态分析与LMS Test.Lab实验模态分析系统对该传动轴总成自由模态台架实验分析对比,初步验证了建立的仿真模型的正确性。分析结果表明传动轴一阶平动模态对应频率为68Hz,对应转速为4080r/min,车速为101.67km/h,位于传动轴工作范围内,是造成传动轴剧烈振动的原因。
(2)通过中间支撑总成静态特性实验测定该型号中间支撑总成刚度为85N/mm,采用弹簧单元连接替代中间支撑总成的方法解决了中间支撑总成复杂的结构对仿真分析的影响,同时为中间支撑刚度参数优化提供指导。
(3)通过理论计算和实验分析传动轴临界转速,其安全系数均大于1.2,满足稳定性要求。
(4)综合中间支撑刚度理论优化和仿真参数优化结果,刚度值选取(225~325)N/mm 范围内最为合适。且在275N/mm 时,加速度降幅5.82%,振幅减小23.17%。

