平板结构法向振速的贝叶斯声学反演方法

刘振宇，张二亮

（郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

由于结构的轻量化设计，现代机械装备中平板类结构应用广泛，但它们在服役过程中容易受激振动并产生噪声。通过将平板类结构表面振速可视化，便于揭示结构的振动噪声的产生与辐射机理，这对平板类机械零件的优化设计和振动控制具有重要指导意义。

传统接触式表面测量振动的方法快捷精确，例如采用加速度计测量，但此类方法容易导致因加速度计自身的质量而使其附着的平板动力学固有性质被改变的问题。非接触式的测量方法能够避免这类问题，例如利用光学仪器进行测量，诸如数字图像相关法[1]或激光多普勒法[2]。近年来，利用麦克风阵列声学测量来重构表面振速的方法引起国内外学者的广泛关注，作为一类实用的非接触式测量方法，逐渐发展起来。

利用声学测量来回溯声源的方法目前有如下几类：基于空间傅里叶变换的近场声全息法通过测量声源面近场的声压，利用二维空间傅里叶变换将声压信息转换到波数域，然后通过传递算子传递相关信息到重建面，最后再经过逆傅里叶变换获得重建面上的振速[3]。基于边界元的方法通过建立声源面和全息面以及预测面之间的振声传递矩阵，利用奇异值分解对该矩阵求逆，并结合测得的声压数据来重建声源表面的振速，该方法适用于不规则的声源面，但计算效率和精度均受许多限制[4]。等效源法通过有限数量虚拟等效源的声场叠加来替代振动体的辐射声场，通过匹配振动体表面的法向振速得到虚拟源的强度[5-6]。基于贝叶斯的声源重建方法能充分融合先验信息，基于边际似然最大化实现正则化参数的寻优，实现了先验信息和似然函数（数据信息）的最佳匹配，能够较高精度地重构声源表面振速[7-8]。

经过技术不断地探索与发展，文献[9]开发了实时近场声全息技术，利用在时间-波数域中格林函数的采样来连续地计算声压场。文献[10]改进了实时近场声全息技术，实现平板表面法向振速的重构。文献[11]利用声压与质点法向速度之间的联系改进了时空域近场声全息技术，实现平板表面瞬时法向振速的重构。文献[12]在贝叶斯方法的基础上利用循环维纳滤波器对循环平稳声源的表面振速进行重构。文献[13]对于稀疏声源的表面重构问题提出了一种迭代贝叶斯聚焦法。文献[14]针对声源重构技术中麦克风阵列位置的布局给出了一种优化方法。

基于近场声压测试数据，应用贝叶斯方法研究平板类结构表面振速的测量问题，首先概述了利用麦克风阵列进行声学测量的方法，然后给出了贝叶斯方法重构声源的具体过程和关键步骤，最后通过简支平板的振动噪声仿真和自由平板的噪声测试实验验证提出方法的有效性。

2 表面法向振速重构的贝叶斯方法

2.1 麦克风阵列声学测量

通过麦克风阵列对平板进行声学测量的方法，如图1所示。假设声源是声源面S上的感兴趣区域，p(ri)是M个麦克风传感器在不同的位置ri，i=1，...，M处测量的声压数据。针对特定频率ω，麦克风阵列测得的声压数据p(ri)与待重构的声源（法向振速）v(r)之间的机理模型为：

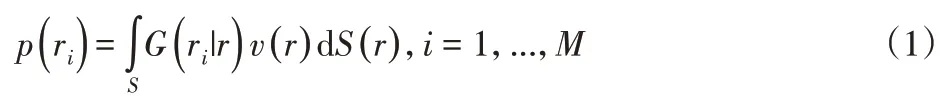
图1 麦克风阵列声学测量Fig.1 Acoustic Measurement by Microphone Array

式中：G(ri|r)—声源面S上的不同位置r与麦克风的位置ri之间的振速-声压转换和格林函数；n(ri)—测量噪声。在文中，为保持符号的简洁，频率变量ω不再标出。声源重建即通过声压数据p(ri)的测量，回溯声源面法向振速v(r)的分布。一般情况下，声源可表示为：

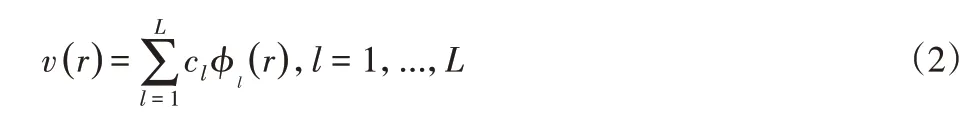
式中：cl—由传感器测量的声压数据所决定的系数；ϕl—独立于测量数据的空间基函数，用于声源空间分布的插值。估计振速v(r) 的问题归结为寻找插值基函数ϕ和声压数据中所包含的系数c的问题。

用p∈CM×1表示所有位置ri处的声压数据，系数c∈Cl×1和测量噪声n∈CM×1的第i个元素分别为ci和n(ri)。式（1）的矩阵形式为：

其中，G的元素可表示为：

利用传感器测得的声压数据重构出声源v(r)，r∈S涉及到传播算子G的伪逆，重构结果往往是不适定的，存在不唯一性和不稳定性，需要正则化策略以获得满意的反演结果。

2.2 贝叶斯方法

本工作应用贝叶斯声源反演方法[7]，研究平板结构的法向振速重构。如上所述，用Φ和c来表示插值基函数和系数，法向振速分布表示为v(c，Φ) 。贝叶斯方法的思想是将声压数据下的振速分布视为通过c和Φ参数化的随机场[v(c，Φ)|p（]其中［］表示随机变量的概率密度函数）。通过后验概率分布[v(c，Φ)|p]的最大化，获得最优参数

基于贝叶斯公式，后验概率密度函数可以表示为：

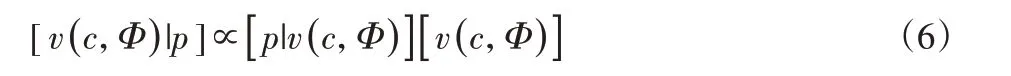
式中：∝—正比例；[p|v(c，Φ)]—似然函数，表示在给定一个振速分布v(c，Φ)下观察到测量声压数据p的概率；[v(c，Φ)]—先验概率分布，表征关于振速分布的所有先验信息（物理信息，专家知识等）。

根据中心极限定理，测量噪声n在频域内服从循环复高斯分布，即[n]=CN(0，λ2IM)，其中λ2代表噪声的平均功率，IM是M×M单位阵。那么测量声压的概率密度函数（似然函数）为：

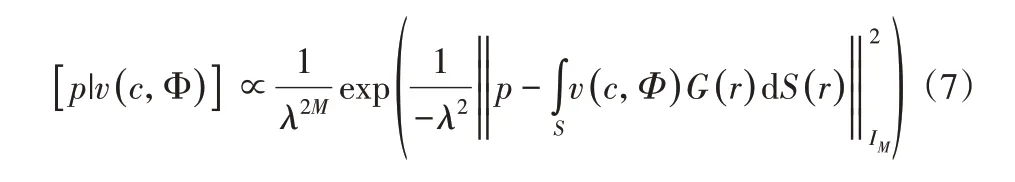
假设先验概率密度函数[v(c，Φ)]也服从循环复高斯分布，即[v(c，Φ)]=CN(0，γ2IM)，其中，γ2—声源的平均功率；Iv—单位矩阵。此时法向振速的空间协方差函数定义为：

孔径函数的作用是通过获取振速（声源）的先验空间位置信息，限定平板结构振速重构的区域，其原理，如图2所示。结合空间位置先验信息，振速的先验概率分布可以表示为：

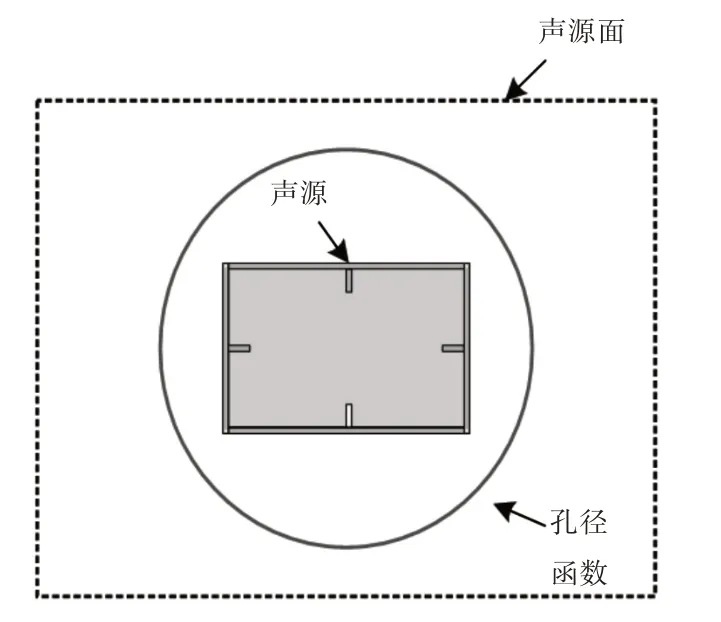
图2 孔径函数 的概念解释Fig.2 The Explanation of Aperture Function

将似然函数和先验概率分布代入贝叶斯式（6），得到后验概率密度函数，对其取负对数，得：

将平板表面均匀划分N个单元，那么相应得到格林函数G∈CM×N。对格林函数进行奇异值分解，G=USVH，得到参数和L：

最后，振速的反演结果为：

式中：η2—正则化因子，η2=λ2/γ2。η2的最优值可以通过边际似然最大化来获得。也就是：

式中：yl=UH p；sl—S对角阵上的元素。

3 仿真算例

3.1 仿真方案

仿真用的矩形简支平板（1×1）m，厚度h=0.002m，弹性模量E=2×1011Pa，密度ρ=7800kg/m2，泊松比μ=0.3，平板的瑞利阻尼系数α和β分别为10-2和10-4。声源传播介质为空气，声速c=340m/s。使用的麦克风阵列为直径1m的圆形支架，传感器位置的随机分布参，如图1所示。

平板与传感器所在平面之间距离z=0.2m。采用随机激励，且作用于平板中心。通过ANSYS软件计算简支平板的固有频率与模态振型数据，然后利用模态叠加法得到平板表面的时域速度和加速度响应。将平板表面的时域速度数据进行快速傅里叶变换得到频域内平板的理论表面振速。

设置仿真中采样频率为2048Hz，采样时间为40s。基于传感器与平板在声场中的空间位置信息以及平板表面的加速度响应，利用时域瑞利积分生成声场内所有传感器位置处的仿真声压信号。这些声压数据用于法向振速的贝叶斯重构。本例选择孔径函数为边长1m的矩形，以（1～1000）Hz为关心频带，重构平板的表面振速。

3.2 仿真结果

以平板中心位置为参考点，分析重构的表面振速与理论值之间的差异，其对比结果，如图3所示。

图3表明，贝叶斯重构的表面振速和理论表面振速在整个频带内幅值接近，相对误差较小。平板的理论表面振速在86Hz处的分布，如图4所示。该频率下重构的表面振速，如图5所示。可以看出二者吻合很好。

图3 平板表面振速的理论值与重构值Fig.3 Theoretical Value and Reconstructed Value

图4 平板的理论表面振速分布Fig.4 Theoretical Surface Velocity Distribution

图5 平板的重构表面振速分布Fig.5 Reconstructed Surface Velocity Distribution

4 噪声测试实验

4.1 实验方案

为进一步验证贝叶斯方法重构平板表面振速的精度，开展了自由平板振动噪声实验。矩形平板尺寸为（0.4×0.4）m，厚度为0.003m，利用橡皮筋悬挂模拟自由边界条件，如图6所示。实验中所用的阵列支架与仿真算例相同。

图6 激振平板信号采集实验Fig.6 Signal Acquisition Experiment

激振器与平板的中心连接，进行单点随机激振。平板与传感器所在的平面平行且距离z=1m，采样频率为8192Hz，采样时间为300s。在贝叶斯算法中，选择孔径函数为边长0.25m 的矩形。实验室的环境峰值噪声约为50dB。

在矩形平板的不同位置安装加速度传感器，这些传感器记录的加速度数据，经过数值积分得到速度数据，用于验证算法的重构精度。

4.2 重构结果

将实验采集的声压数据应用于贝叶斯方法，得到（0～700）Hz频带内平板的表面振速。其中430Hz处的重构的平板表面振速分布相对于阵列支架的位置，如图7所示。与实际空间位置吻合。

图7 重构表面振速分布（430Hz）Fig.7 Reconstructed Surface Velocity Distribution

以平板的中心为坐标原点，选取平板上位置为（0.05m，-0.1m）的加速度传感器的数据为参考，积分得到振速数据，再通过快速傅里叶变换得到表面振速的测量值。将之与相同位置处的重构表面振速进行对比，如图8所示。可见，平板的振动噪声测试实验验证了本文采用贝叶斯振速重构算法的有效性。

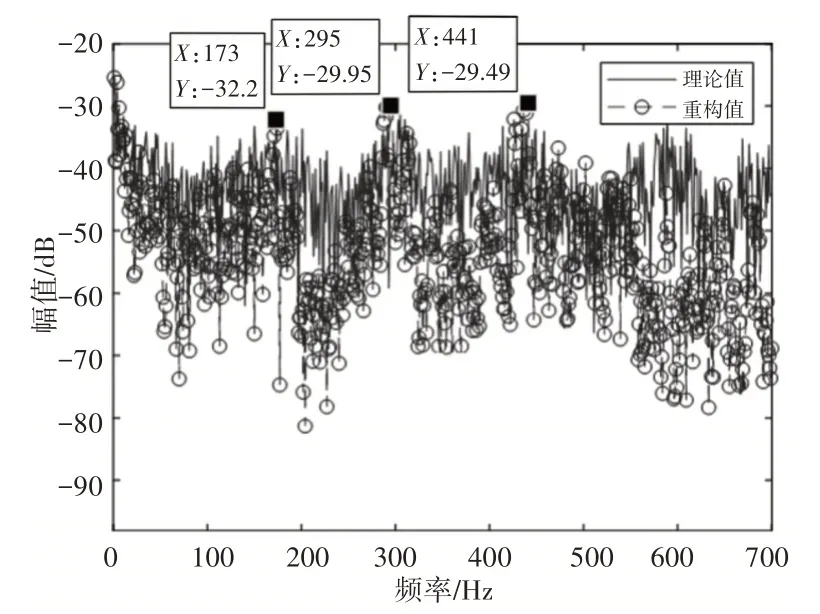
图8 平板的重构表面振速与实测表面振速Fig.8 Reconstructed Surface Velocity and Measured Surface Velocity of Plate

5 结论

利用了平板类结构近场辐射的声压数据，开展了基于贝叶斯方法的表面振速重构应用研究。仿真和噪声实验结果都表明，近场贝叶斯声全息方法是重构平板类结构表面法向振速的有效方法。这将为平板类结构的非接触式振动测试提供新手段，对于开展轻质结构的振动噪声控制和优化设计具有重要意义。