传统谱聚类算法概述

许洪玮

（广东工业大学信息工程学院，广东广州 510006）

聚类算法是要将数据集中具有相似性的数据划分为一类，而将不相似的数据划分为不同类，最终实现将数据集划分为若干类。其主要过程包括确定样本数据、获取特征、计算特征值、计算相似度、评估聚类结果的有效性等步骤。聚类算法可以按照聚类原理分为：划分方法、层次方法、基于密度的方法、基于网格的方法、基于模型的方法、基于图论的方法等。

谱聚类算法（Spectral Clustering Algorithm）与K-means算法、EM算法和模糊C均值聚类算法（Fuzzy C-mean Clustering,FCM）等传统的聚类算法不同，不需要聚类对象具有凸球形或其他特定形状，就能在任意形状的样本空间上实现聚类。谱聚类算法的思想源自谱图划分理论[1]，该算法的核心思想是：计算样本数据集所描述成数据点的相似度矩阵，通过特征分解，计算矩阵的特征值和特征向量（也就是谱信息），然后选择合适的特征向量作为数据的低维空间描述，之后对选择的特征向量应用K-means等方法进行聚类，聚类的结果最后映射回原数据空间。谱聚类算法是一种点对聚类算法，其本质是用图的最优划分思想处理聚类问题，解决了高维特征向量的奇异问题，因为它只和数据集的规模有关，而与数据集的维数无关。

以下几个方面，是谱聚类算法相比传统聚类算法的优点：

（1）谱聚类算法不对数据集的全局结构进行假设，其思想简单、实现方便；

（2）谱聚类算法是一种点对聚类方法，它与数据的特征向量维数无关，只与数据的个数有关，可用于解决高特征向量维数的奇异性问题；

（3）谱聚类算法可以通过特征向量分解，在放松了的连续域中获得全局最优解。

因此，谱聚类算法成为解决实际应用问题的新方法，可应用于图像分割、视频分割、语音识别、文本挖掘等研究领域的问题解决。尽管谱聚类方法在一些问题的解决上取得了不错的效果，但还有许多值得深入研究的问题。

本文主要对一些基本算法进行概述，包括：图谱和谱分解的基本概念、传统谱聚类算法的概述、基于密度聚类算法概述和评价指标Rand Index。

1 图的谱及图的谱分解概述

谱图划分理论是谱聚类算法的思想来源，图的谱分布与图的结构之间的对应关系是近年来兴起的相当活跃的研究课题，其中特征值及相关概念是研究的集中方向。下面简要介绍谱的基本概念[2]。

图的表示方法为G=(V,E)，其中V={v1,v2,...,vn}是顶点或点的集合，E={e1,e2,...,em}是连接任意两个点的边的集合，顶点的个数n=|V|，边的个数m=|E|。如果连接顶点u、v的边euv的值是无穷的，则称顶点u、v是不相邻的，否则是相邻的；如果边e1和e2有一个共同的顶点，则称边e1和e2是相邻的，否则是不相邻的。以顶点v为端点的边数称为顶点v的度，记为dv。

如果两个顶点之间的边数不止一条，则称为多重边；如果一条边的两个顶点是相同的，则称为边的环。不含有多重边和环的图称为简单图，含有多重边的图称为多重图。每一对顶点间都有边相连的无向简单图称为完全图。本文所讨论的图全部都是完全图。

记A(G)表示图G的邻接矩阵，有如下的定义：

定义（1）图G的特征值就是对应邻接矩阵A(G)的特征值，用λi(i=1,...,n)表示。

定 义（2）图G的n个 特征值λi(i=1,...,n)的序 列（λ1≥λ2≥...≥λn）称为图G的谱。

定义（3）图G的最大特征值λi称为图G的谱半径。

定义（4）图G的拉普拉斯特征值就是拉普拉斯矩阵L(G)的特征值。

拉普拉斯矩阵L(G)可表示为：L(G)=D(G)-A(G)，其中D(G)是图G的度矩阵，A(G)是图G的邻接矩阵。

图的特征值是图的同构不变量，是图论的一个重要研究课题，而我们希望通过谱方法来实现对图的描述。下面简要介绍图的谱分析与谱分解。

通过计算图的邻接矩阵的模可以得到图的谱特征，我们以特征值的次序来决定特征向量的次序。

如果用邻接矩阵的特征值来构成图G的谱特征，那么图G的向量B可表示为：

其中λ1≥λ2≥...≥λn，这一向量就表示了图G的谱。

如果用拉普拉斯矩阵的特征值来构成谱特征，那么图的向量B可表示为：

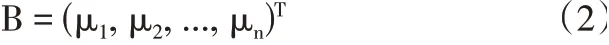
其中μ1≥μ2≥...≥μn，这一向量表示图G的拉普拉斯。

图的谱方法是通过图的谱特征向量来表示图的结构信息，这样，一旦获得图的特征向量，那么一张图就可以在特征空间上表示为一组数据，这就成为进一步处理图数据的基础。

图的谱方法主要有两个方面的优点。第一：计算复杂度较低。因为图的谱方法可以只选取部分有效的特征来表达图的信息，这样就不用对图本身进行计算，其计算复杂就被大大降低了。第二：可以用于表达海量数据的图。海量数据的图需要用一个好的数学表达式才能很好地表达，而寻找一个好的数学表达式往往是非常苦难的，但图的谱方法就可以实现这种表达。

图的谱方法自身也存在一些不足。因为选取的谱特征是有限的，这样就不能完整地表达图的全部结构信息，从而造成计算精确度的不够；另外可能会出现不同的图但它们的谱特征表达是一样的，也就是一谱多图的情况。

2 传统谱聚类算法概述

谱聚类（Spectral Clustering）是基于图论的方法把聚类问题转换为组合优化问题，具体来说，就是将数据集表示成一个图中所有顶点的集合，用图相应的边的权重表示数据之间的相似度，这样就可以利用图论和图形学的原理进行分析并实现数据聚类。

若把图中的顶点V表示成数据集中的每一个样本，连接顶点间的边E上的权重值W相应表示成样本数据间的相似度，这样就可以用无向加权图G=(V,E,W)表示整个数据集及数据样本间的关系。因此，可以应用图的划分方法解决样本数据集的聚类问题。图论的最优划分理论，就是使得被划分成的子图内部相似度尽可能大，而划分成的若干子图之间相似度尽可能小[3]。图划分准则常用的有：规范割集、比例割集、平均割集、最小割集以及最小最大割集等划分准则。由于图划分问题的本质是组合问题，其最优解求解是一个NP难题，可以通过相似度矩阵或拉普拉斯(Laplacian)矩阵的谱分解方式来解决，这种处理方法统称为谱聚类。

谱聚类算法根据不同的图划分准则有不同的具体实现方法，下面是由Andrew Y.Ng[4]提出的谱聚类算法。

如果要将样本空间上的数据集S={s1,...,sn}，划分成k个子集（类），则具体实现步骤为：

（1）构造数据集S的相似度矩阵A，矩阵A的构造公式为：

（2）对角矩阵D的第（i,i）个元素的值是矩阵A的第i行全部元素的累加和，这样就可构造矩阵L，其计算公式为：

（3）计算矩阵L的特征值和特征向量，x1,x2,...,xk是最大的k个特征值所对应的特征向量，可得到n行k列的矩阵X，X=[x1x2...xk]；

（4）将矩阵X归一化为矩阵Y，归一化公式为：

（5）对矩阵Y使用K-means算法进行分类，矩阵Y的第i行对应数据集S的第i个数据Si;

（6）矩阵Y的第i行所属的类，就是数据集S中的数据si所属的类，这样就完成了对数据集的分类。

这里，尺度函数σ2是敏感参数，控制着两个数据点之间欧氏距离的衰减程度，也直接影响着随后的聚类效果。

谱聚类算法虽然能在一些数据集上取得较好的聚类结果如环形数据集，但对于分布比较复杂的数据集，如螺旋形数据集，该算法的聚类结果就差强人意了。这是因为谱聚类算法是通过高斯核函数来表示数据间的相似度关系，也就是在新的空间对原始的数据关系，欧氏距离关系，重新建立起映射关系，而这种映射关系只对简单的空间分布有效，而不能正确反映空间分布比较复杂的数据关系。鉴于该算法的不足之处，研究者们不断提出了新的改进方法。

3 DBSCAN聚类算法概述

DBSCAN[5]聚类算法是由Martin Ester等人在1996年提出的，该算法是典型的密度聚类算法，通过高密度连通性来快速发现任意形状的类，并同时排除噪声的干扰。

DBSCAN算法的核心参数有最小半径Eps和最少对象数目MintPts，就是在其规定半径Eps范围内，所包含的数据点数不能少于给定的数目MintPts。DBSCAN算法定义了密度可达的概念，是在一个类能够被其中任意一个核心对象点所确定的前提下，划分出数据集的各个类的。首先，选中数据集P中的任意对象点m，查找符合Eps和MinPts条件并从对象点m密度可达的所有对象点。如果对象点m是核心点，则根据算法可以确定一个类；如果对象点m是边界点，且点m无法密度到达其他数据点，则点m被暂时标注为噪声点。然后，算法选取下一个数据点，并按同样的方法进行。

DBSCAN算法步骤：

（1）输入参数值Eps和MinPts；

（2）选取数据集中的任意一个点m，对其进行区域查询；

（3）如果点m是核心点，则查找从m点密度可达的所有点，并形成一个类；

（4）否则，点m被暂时标注为噪声点；

选取下一个数据点，重复步骤（2）到（4），直到处理完数据集中的所有点。

由于DBSCAN算法的参数Eps和MinPts是全局参数，比较难以确定，都必须靠先验知识来设定，而且这两个参数直接影响着算法的聚类性能，这样就可能导致部分密度小的聚类被处理为噪声；而对于边界点，若该点附近密度较大就会形成单连通，出现错误分类结果。

4 聚类性能的评价指标

聚类算法的最终结果是实现数据集的划分，而聚类结果的好坏需要进行有效性和质量评价。聚类质量的评价方法可以分为内部度量、外部度量和相对度量三类，并且每种度量方法有不同的计算方式。这里对外部度量方法中的一种计算方式——Rand Index[6]进行介绍。

Rand Index是由Milligan和Cooper提出的一种聚类质量评价指标，用于衡量聚类结果与数据的外部标准类之间的一致程度。

对于数据集X={x1,x2,...,xn}，假设S={s1,s2,...,sk}和R={r1,r2,...,rk}是数据集X的两种不同划分，其中S是外部标准划分类，而R是算法的聚类结果。那么Rand Index的计算公式如下：

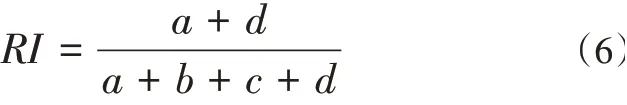
公式(6)中a表示S和R中都属于相同类的个数，b表示属于S中一类而不属于R中同一类的个数，c表示属于R中同一类而不属于S中同一类的个数，d表示都不属于S和R中同一类的个数。a和d反映了两种划分的一致性，而b和c放映了不一致性。

Rand Index的数值在[0,1]的区间内，其值越大，则表示两种划分的一致性就越高，当两种划分完全一致时，Rand Index取值为1。

5 结语

近年来，谱聚类算法成为聚类算法的热门研究课题，也不断涌出新算法和新研究成果。该算法可以很好地应用于解决具有非凸分布的实际问题，而如何构建一个正确反映数据间关系的相似度矩阵，是谱聚类算法研究的重点难点。希望本文对传统谱聚类算法的介绍可以对初学者提供初步的学习借鉴。