Hadamard 缺项幂级数及双曲完备极小曲面

张建肖，刘晓俊

（上海理工大学 理学院，上海 200093）

1 问题的提出

极小曲面理论是近年来发展较快的一个数学分支，它广泛存在于自然界当中。关于极小曲面的很多问题也源于自然界，这就为学者们更好地了解极小曲面的性质创造了有利条件。1954 年，Calabi[1]提出了以下2 个猜想：

猜想1包含于 R3的半空间中的完备极小曲面一定是平面。

猜想2R3中的完备极小曲面是 R3中的无界子集。

1980 年，Jorge 等[2]利用Runge 逼近定理证明了存在位于 R3中2 个平行平面之间非平坦的完备极小曲面，从而否定了猜想1。

1996 年，Nadirashvili[3]利用Runge 逼近定理否定了猜想2，证明了存在极小浸入到 R3中单位球的具有负Gauss 曲率的完备极小曲面。但是，他们的证明只是表明存在相应的极小曲面，没有给出具体的满足条件的极小曲面的例子。

于是，这就需要学者们对于能否构造出具体的完备极小曲面实例进行深入的研究。

1992 年，Brito[4]利用Hadamard 缺项幂级数构造了 R3中位于2 个平行平面间的完备极小曲面族，给出了实例，得到定理1。

由此，只要令Weierstrass 表示中的f=1且g=h′，即可得到 R3中2 个平行平面间的完备极小曲面族。于是，研究发现Hadamard 缺项幂级数与完备极小曲面存在紧密的联系。

根据定理1 的条件a 和b 可知，当j充分大时，趋向于 ∞ 的速度远大于趋向于0 的速度。于是，自然地可以提出如下问题：能否减弱此条件。

受到1991 年孙道椿[5]证明方法的启发，作者继续研究能否构造出位于 R3中2 个平行平面间的完备极小曲面，得到定理2。

2 定义与符号

设 Δ为复平面 C 中的单位圆盘，现讨论由 Δ参数化的完备极小曲面。

现给出Hadamard 缺项幂级数的定义。

定义1[6-7]若f(z)=是一个收敛半径为1 的幂级数，其中，z∈C，且满足

nj+1/nj≥q＞1,j=1,2,···，

则称f(z)为Hadamard 缺项幂级数。

关于缺项幂级数的更多结果可参见文献[8]。

定义2[9-10]R3中平均曲率恒为零的曲面称为极小曲面。

定义3[10]设D是 R2中的开子集，γ:[0,a)→D是D内的连续曲线。若对D的任意紧子集K，存在t0，0＜t0＜a，对任意t∈(t0,a)，有 γ(t)∉K，则称 γ是发散的，记作 γ→∂D。

定义4[10]设I:D⊂R2→R3是一个浸入，且D具有诱导度量，即‖v‖D=，这里I*:Tz(D)→TI(z)(R3)是浸入I的切映射。若对于任意的光滑发散曲线 γ:[0,a)→D，其在诱导度量下的弧长为无穷大，则称浸入I:D⊂R2→R3是完备的。

定义5[11-13]设单连通区域D⊆C,f:D→C 是D上的全纯函数，g:D→是D上的亚纯函数，满足若z0是g的k(≥1)重极点，则z0是f的 2k重零点；反之亦然。令则称x=(x1,x2,x3):D→R3为极小曲面M的Enneper-Weierstrass 表示，或简称Weierstrass 表示，(f,g)称为极小曲面M的Weierstrass 表示对，由(f,g)生成的极小曲面可记为M(f,g)。

此时，M上的度量定义为

3 定理2 的证明

对于任意的k∈N，令

每一个Rk都是一个宽度为的环，且对于充分大的k，每个环形Rk互不相交。

由式(3)可得，

另一方面，由定理2 的条件b 可得，存在k2∈N,k2≥k1，使得

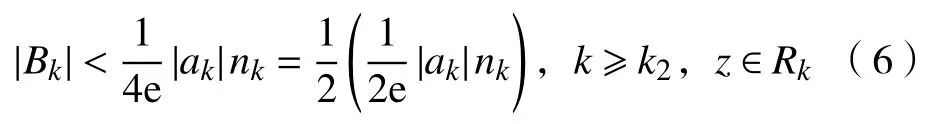
因为，当 0＜x＜1时，ln(1-x)＜-x，又根据定理2 的条件a 可得，

由定理2 的条件b 可知，对于充分大的k，nk+1＞2nk，又由于当x＞a时，函数xe-x/a是递减函数，故

再由定理2 的条件b 和式(7)可得，存在k3∈N,k3≥k2，使得

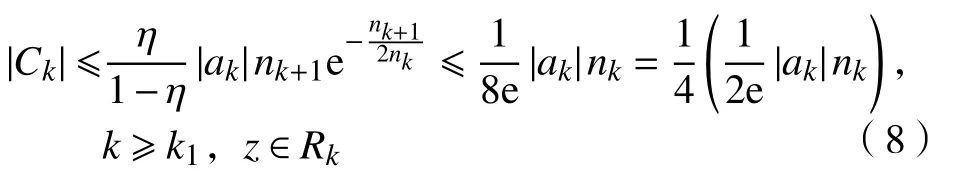
由式(4)～(6)和式(8)可得，存在k0∈N,k0≥k3，使得

取 Δ内的发散曲线 γ，对于任意的k≥l，l∈N，γ必定穿过Rk，则

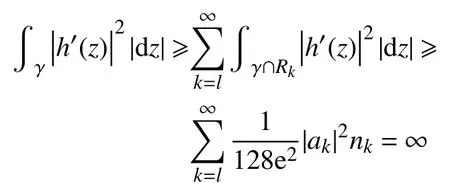
根据定理2 的条件c 可以得到最后的不等式。所以，定理2 得证。

设h(z)=，z∈C，其中，aj=,nj=(16e)j。易得h(z)满足定理2 的条件a～c，但不满足定理1 的条件b。

4 推论

设A(Δ)是由在单位圆盘 Δ内的解析的函数构成的集合。

推论1存在h∈A(Δ)，使h′是 R3中一个完备极小曲面M的Gauss 映射，其中，M位于 R3中的2 个平行平面之间。

证明设M为Weierstrass 表示中取f=1,g=h′所得的极小曲面，其中，h满 足定理2 的条件，则h∈A(Δ)。

由于 λ(z)|dz|=，由定理2 可以得出此度量是完备的，所以，h′是 R3中一个完备极小曲面M的Gauss 映射。又由于

所以，M位于 R3中的2 个平行平面之间。

推论1 的证明过程与Brito[4]的推论相同。