给水厂混凝剂智能投加模型构建与应用
刘洪波,黄剑虹,张国荣,吴 燕,刘丽梅
(1.上海理工大学 环境与建筑学院,上海 200093;2.昆山市自来水集团有限公司,昆山 215300;3.昆山汉元经水水务科技有限公司,昆山 215300)
在城市给水处理中,为去除天然水体中的微小悬浮物及胶体,混凝过程是处理工艺中必不可少的一步。其中混凝剂的用量不仅直接决定了给水厂出水水质的好坏,也影响着水厂生产运营成本。然而混凝过程中涉及许多复杂的反应,同时由于原水水质、水量的不断变化,对混凝剂投加量的判断与控制并不容易[1]。随着信息化与智能化的发展,神经网络已被广泛应用于工业生产过程中,基于神经网络的混凝剂智能投加模型在给水厂中也有所应用[2]。但传统的智能投加模型的建立缺乏大量数据支持,且对模型如何有效融入智慧水厂建设中的研究不足。本文以华东地区某给水厂为基础,对混凝剂智能投加模型的构建以及在给水厂混凝剂加药系统智慧化改造中的应用作了更深一步的研究。
1 水厂数据处理与分析
1.1 水厂大数据清洗
建模所用数据取自华东某给水处理厂的在线记录数据,原水指标共6 项,包括浊度、流量、溶解氧含量(DO)、pH、总磷(TP)和氨氮。混凝剂投加量数据取自投加泵的流量记录,所用混凝剂为液态PAC,氧化铝含量10.3%~10.8%。所有数据每5 min 测一次,时间跨度从2020 年1 月至2022 年11 月,总计约250 万个数据记录。水厂运行过程中,由于各种因素的影响,记录数据中包含了少量的误差、异常值以及缺失值,有必要在建模前对水厂积累的大量数据进行清洗。
由于测量设备故障、设备维护与清洗等原因,在数据记录中包含的远超常理范围的原水水质指标测量记录可以被认为是粗大误差,采用拉依达准则结合数据可视化图将这类误差剔除。拉依达准则通过假定数据为近似正态分布,将偏离均值3 倍标准差的观测值作为坏值剔除[3]。呈现非正态分布的部分数据则结合数据可视化图,划定最小与最大观测值,将不符合误差要求的数据按不合格数据进行选择性剔除。
同时在数据记录中,受测量设备不稳定与原水水质波动等随机因素的影响,存在大量不规律的随机误差。数据预处理中常用平滑滤波来消除随机误差[4],以波动较剧烈的2021 年9 月15 日的浊度数据为例,采用五点三次平滑滤波方法对数据进行处理。如图1(a)所示,经过平滑滤波处理后,波动较小的随机误差均得到了处理,但存在一些偏离较大的随机误差依然难以消除。对于这类随机误差,可以看作连续数据局部的异常值,使用基于密度的局部离群因子(local outlier factor,LOF)算法对其进行剔除,之后使用K最近邻插补(K-nearest neighbor imputation,KNN)算法对剔除后的空缺数据进行填补。LOF 算法是一种基于密度的无监督机器学习异常检测方法,它通过计算每个样本在给定的领域内相对于其临近点的密度局部偏差,对每个样本计算异常得分,密度远低于其临近点的样本,异常得分也高于正常点,即可辨别为异常的离群值[5]。KNN 算法则在给定的缺失样本K领域内,将距离缺失样本最近的K个样本的数值加权以估计缺失的数值[6]。

图1 随机误差处理示例Fig.1 Example of random error processing
将上述处理手段加以结合,形成一系列随机误差的组合处理方法,最终处理的步骤为:a.LOF 算法剔除异常值;b.KNN 算法填补剔除后出现的空值以及原始数据中的缺失值;c.对数据进行五点三次平滑滤波处理。对于水厂的一维数据,将每组数据按时间顺序编号,利用网格来做最近邻查询[7]。在LOF 算法与KNN 算法的计算中,均以样本点的5 个近邻为给定领域,同时LOF 的计算中将异常得分大于1.2 的样本识别为异常点加以剔除。处理前后数据对比如图1(b)所示。
由图1(b)可知,相比未经过处理的数据,经组合处理的数据中局部的异常值已经消失,随机噪声也大为减少。经过处理后,数据剩余220 万个,各项数据整合后为31 万组数据,相比250 万的原始数据,本研究数据清洗方式的数据损失量也在可接受的范围内,后续使用经过组合处理的数据建立的模型也有明显优势。
1.2 原水指标重要性分析
虽然对混凝剂投加后水体中的混凝与沉淀反应已有大量的理论分析,但在水厂实际的生产中,原水中各因素对混凝过程的影响非常复杂[8]。因此,混凝剂的投加过程实际是一个信息不清晰的灰色系统,使用灰色关联度分析的方法对原水指标与混凝剂投加量的联系进行评估。灰色关联度分析通过比较不同数列曲线的几何形状相似程度来判断数据间联系紧密程度,对数据分布规律与样本数量均无要求,在水环境指标的分析中已有应用先例[9]。
由于各项指标有不同的计量单位,存在量纲和数据尺度上的差异,不便于比较,在分析前使用标准化的方式对数据进行无量纲化处理[10],计算公式如下:

由极大值原理可知0
对无量纲化后的数据进行灰色关联度分析,计算各原水指标与加药量的灰色关联度R。R值越大代表关联程度越高,在对混凝剂加药量的分析中,即代表了原水指标的重要程度越高。混凝剂加药量的灰色关联度分析结果如表1 所示。
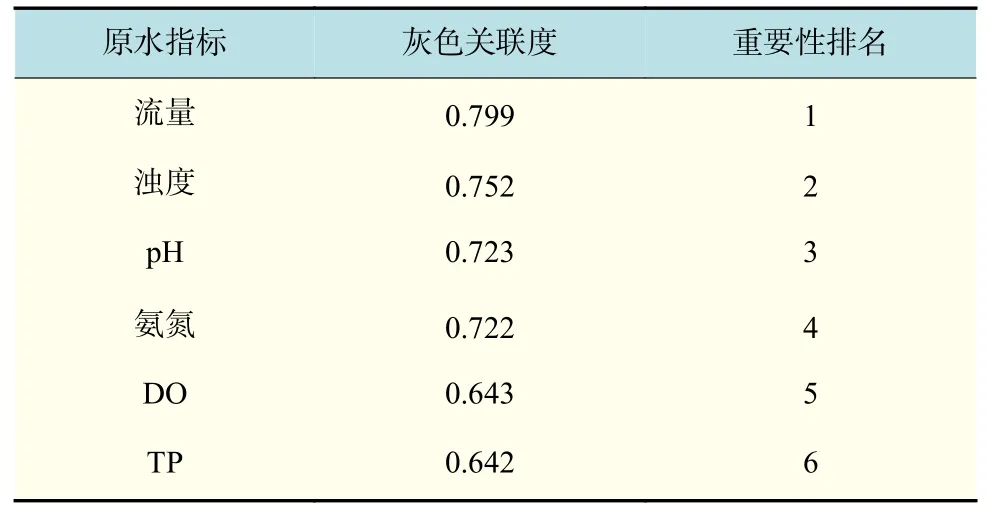
表1 原水指标与加药量灰色关联度分析结果Tab.1 Grey correlation degree analysis results of raw water indexes and dosing flow
图2 以矩阵热力图的形式展示各指标之间的灰色关联度,其中,x轴方向为比较序列,y轴方向为参考序列。

图2 灰色关联度矩阵热力图Fig.2 Heatmap of grey correlation degree matrix
通过灰色关联度结果的分析可知,与混凝剂加药量联系最紧密的原水指标为流量(R=0.799),其次为浊度(R=0.752),这之后是灰色关联度值接近pH 与氨氮(分别为0.723 与0.722),剩下的DO与TP 的灰色关联度值相较而言则大为降低(分别为0.643 与0.642),可以认为对加药量影响极小。这之中,原水流量改变后,生产中必然也会对混凝剂投加量进行相应调整,同时流量的改变也会带来反应池水流速度梯度的变化,对混凝效果的影响至关重要。浊度则是衡量混凝沉淀效果的指标,原水中的浊度作为混凝剂投加过程中需要削减的主要指标,与加药量有着相同的变化趋势。进水pH 较高时,部分铝盐转化为溶解性的Al(OH)4-,造成混凝剂吸附架桥与网捕卷扫能力下降[11]。考虑到华东某水厂原水pH 范围在6.8~8.6 之间,存在偏高的问题,pH 与混凝剂加药量的正相关关系应该取决于pH 升高时为保证混凝效果而增加的加药量。对于氨氮,在水体中氨氮大多以游离氨的形态存在,难以通过混凝沉淀反应去除,其对混凝沉淀过程的影响也很小[12]。由于水厂氨氮检测设备的最小示值较大而实际数值较小,造成氨氮的测量记录值在几个数值间变化,从而与加药量数列曲线的几何形状相似。
2 混凝剂加药量模型建立
2.1 BP 神经网络模型与贝叶斯优化
BP 神经网络是一种有多层神经元的前馈神经网络,数据从第一层的输入层进入网络,经过中间层为隐藏层,最后从输出层得到结果。在BP 神经网络的训练中,计算网络输出值与真实值之间的损失值,应用反向传播算法(back propagation,BP),将损失从输出层反向传播至输入层,调节各层连接间的权重值与偏置系数[13]。经过训练的神经网络损失值不断减少,最终可以近似于任意的复杂函数。然而在上述网络建立与训练过程中,有大量的参数需要预先人为设置,其值的大小对BP 神经网络的性能有决定性影响。常用的神经网络参数的估计方法如网格搜索与随机搜索十分耗时,为此有学者提出了贝叶斯优化等算法以提高优化效率。
贝叶斯优化是基于一种序贯的先验优化方式,在确定优化的目标函数以及函数定义域后,先在目标函数上随机取几个观测点进行观测。根据观测结果,使用概率代理模型对目标函数的分布进行估计,在估计的基础上计算采集函数以选择下次迭代过程中观测点的位置。由此迭代,直至找到目标函数值最优的点[14]。相比于传统的优化算法,贝叶斯优化能够以更少的迭代次数,准确快速地得到参数的最优解[15],在面对大数据建模时可节省大量时间。
本研究基于Python 语言,对经过预处理后的共31 万组数据进行建模与评估。在建模前,抽取部分数据使用贝叶斯优化算法对BP 神经网络的结构与参数进行优化,后利用优化参数建模以实现混凝剂投加量的预测。
2.2 模型训练
使用经过预处理的数据,共25 万组数据用于训练,将全部的6 项原水指标作为输入训练BP 神经网络。为加快训练时损失函数的收敛速度,使用经标准化处理的数据进行训练,同时使用贝叶斯优化算法对BP 神经网络的参数进行优化。优化的参数为:神经网络隐含层数量、隐含层神经元数量、正则化系数、随机批次大小、动量因子、学习率。
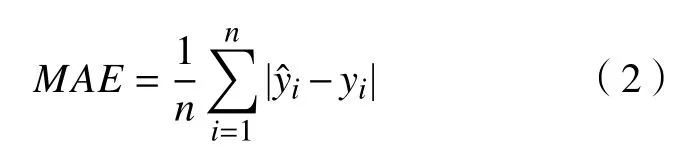
式中:n为用于预测数据的数量;与yi分别为预测值与真实值。
如图3 所示,随着迭代的进行,目标函数的最小值逐渐下降,经过50 次迭代后,贝叶斯优化得到最优的结果。此时模型对应的参数:隐含层为5 层;隐含层神经元数量为412;正则化系数为0.000 01;随机批次大小为75;动量因子为0.268;学习率为0.137。

图3 贝叶斯优化过程中最优目标函数值Fig.3 Optimal objective function value during Bayesian optimization
使用贝叶斯优化后的参数对神经网络进行训练,同时设置动态的学习率,在训练过程中划分2.5 万组数据作为验证集,训练中验证集数据预测的R2评估值若不能在10 次训练周期中上升0.000 1,即将现有学习率除以5,持续此过程直到学习率再也无法减小。训练过程中训练集损失、验证集R2与学习率的变化如图4 所示。
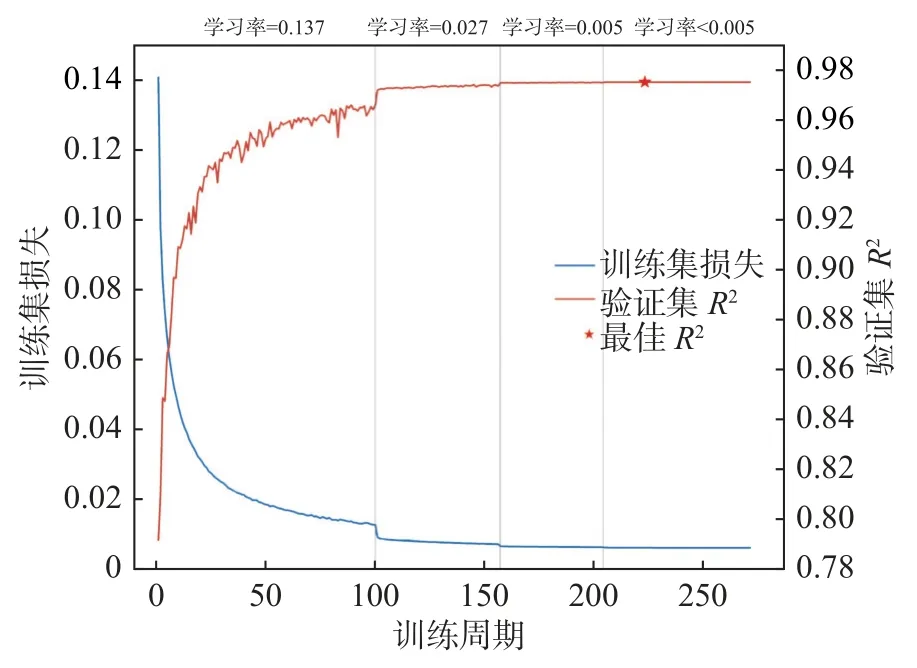
图4 BP 神经网络训练过程Fig.4 Training process of BP neural network
随着训练的进行,训练集损失逐渐下降,验证集R2逐渐上升,同时每当学习率改变时训练的效果会有突然的提升。第223 次训练周期后,验证集R2不再上升,而训练集损失仍逐渐下降。此时模型有过拟合的风险,于是设置训练在经过223 次训练周期后提前停止。
3 模型评估
使用测试集中数据对模型进行评估,其表现反映模型在新数据中的泛化能力,选取约6 万组未经过训练的数据对模型进行测试,占处理后总数据量的20%。评估模型预测性能的指标除MAE、R2外,还有平均绝对误差百分比(MAPE),模型评估中MAE与MAPE的值越低、R2的值越高,即代表模型的效果越好。MAPE计算公式如下:

式中:n为用于预测数据的数量;与yi分别为预测值与真实值。
除使用经过预处理的数据以及全部的6 项原水指标作为输入的模型A 外,以与模型A 相同的优化与训练方式,使用未经组合处理的数据训练模型B,以评估本研究提出的数据清洗方式对模型性能提升的表现;同时,使用在重要性分析中排名前4 的原水指标的数据训练模型C,探究在重要性分析中排名靠后的指标对加药量的影响。表2为对各模型预测性能的评估。

表2 不同模型预测性能比较Tab.2 Performance comparison of different models
比较不同模型预测效果的差异,其中模型A 的评估效果相较于模型B 有明显提升,如模型A 的MAE评估值相比模型B 提升了43.9%,MAPE提高了46.5%。这表明本文提出的随机误差组合处理手段有效地降低了原始数据集中的随机误差,极大改善了所建模型的性能。而对模型C 的评估显示,其建模效果相比另外两个模型差距较大,说明TP 与DO 两个原水指标对混凝剂投加量仍有一定影响,不能在建立模型时剔除。
对模型A 的预测误差进行进一步分析,同时在测试集数据中加入与原始数据中随机误差分布相同的随机噪声,以此测试模型预测效果的鲁棒性,如图5 所示。结果表明,加入噪声后R2的评估值为0.97,MAE的评估值为4.16 L/h,MAPE则均在3%以内,虽相比原测试集稍有降低,但总体效果与原测试集接近,模型具有较高的鲁棒性。同时可以看到,模型预测值与实际值的分布大体一致,预测值的偏离较小且呈现对称分布,可以认为模型有效地拟合了实际数据的信息。
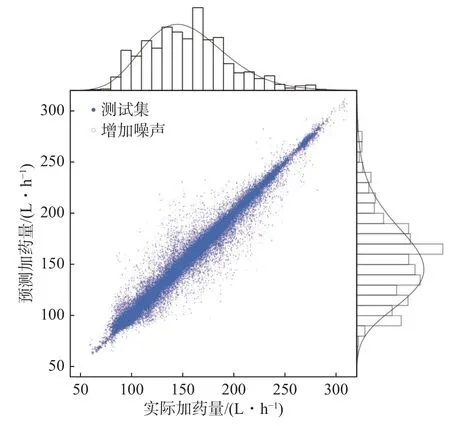
图5 模型A 预测误差分析Fig.5 Prediction error analysis of model A
经过综合评估,模型A 的性能满足水厂生产过程中对混凝剂投加的要求,其建立过程中数据处理与训练的方法有一定的参考价值。
4 模型应用展望
华东某饮用水处理厂的生产过程具有较为完善的自动化建设基础,但混凝剂投加量的决定依然基于人员的经验判断。为此,展望未来的水厂智慧化改造,将本文建立的BP 神经网络模型应用于水厂混凝剂智能投加控制中,智能加药在线控制系统的框架如图6 所示。智能加药系统在接收并处理水质在线检测设备传递的信息后,将信息向下传递,主要有混凝剂投加量预测与数据分析结果可视化两项功能。
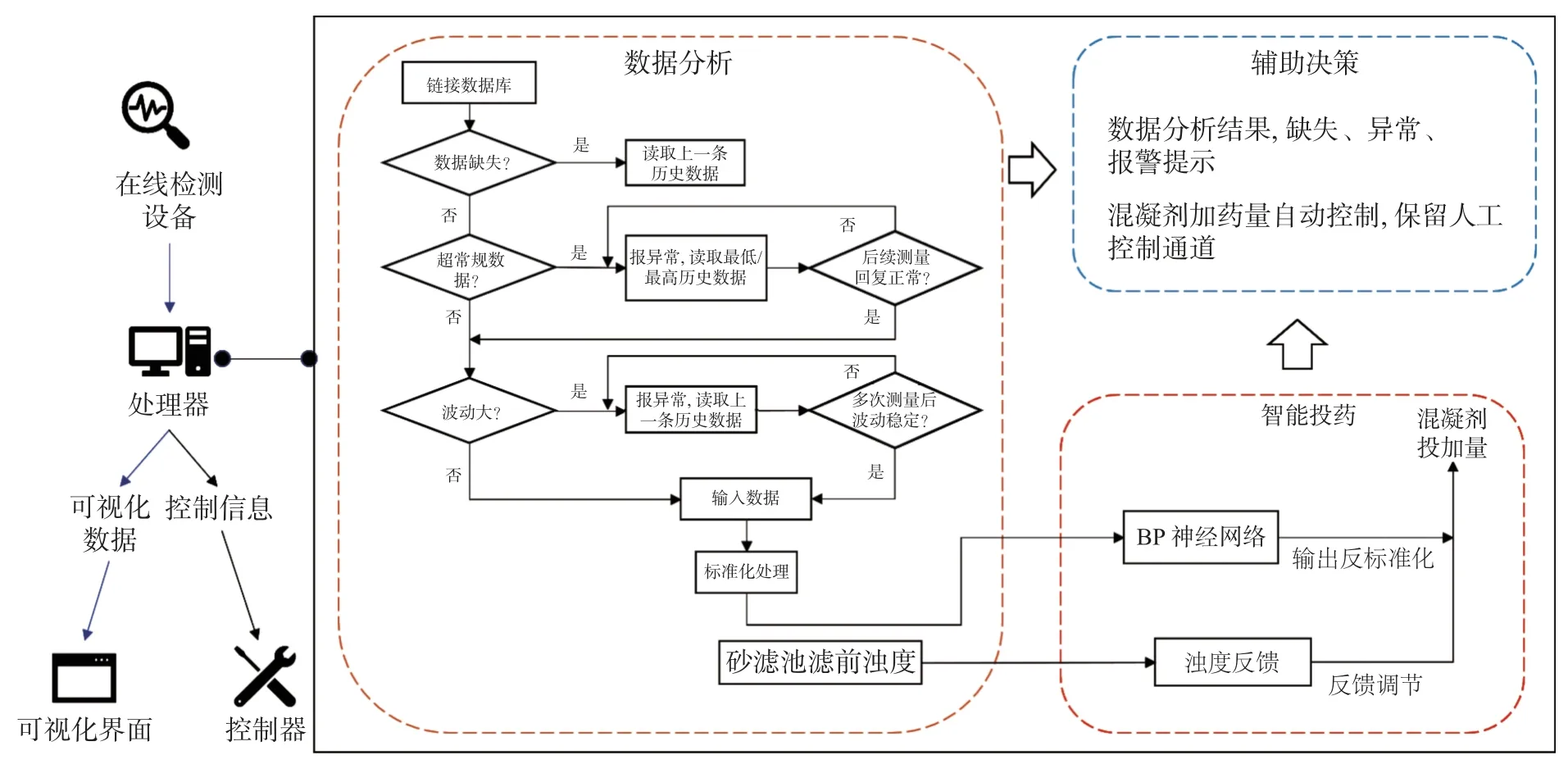
图6 智能加药在线控制系统框架Fig.6 Framework of intelligent dosing online control system
水质在线检测设备得到的原水水质信息是BP 神经网络模型预测加药量的依据,但由于检测设备故障或原水水质波动的原因,偶有出现缺失或异常检测数值。在数据分析中,先将此类数值识别并替换,再向下传递至神经网络模型中,使得混凝剂投加量的预测结果更为准确。另外,引入砂滤池滤前浊度作为反馈,对预测投加量进行微调,从而使出水水质更为稳定。同时,将数据分析与处理的过程实时地展示在可视化平台中,更好地辅助人员决策。
5 结束语
混凝是饮用水制水过程中最重要的工艺,准确的混凝剂投加量对制水成本与出水水质有着重要意义。本文使用多种方式对采集的水厂历史运行数据进行清洗,并对各原水指标与加药量的关系进行分析。使用BP 神经网络对浊度、流量、pH、溶解氧含量、总磷和氨氮建模以预测混凝剂的投加量,同时利用贝叶斯优化对BP 神经网络的超参数优化求解。评估结果显示所建模型能够满足水厂对混凝剂投加的要求,并在其基础上搭建一套智能加药在线控制系统的框架,以展望未来在水厂中的实际应用。但由于本研究条件的限制,收集的建模数据中缺少如温度、碱度与天然有机物等在混凝机理中也存在一定影响的因素。后续可改进研究条件,获取更多数据,探究更多影响因素与混凝剂加药量之间的联系,进一步提高模型精度。未来也可在水厂中进行实际部署,获得更多的数据与运行经验,并使用更加前沿的机器学习技术,在提高模型泛化能力的同时对控制系统加以优化。

