基于分层高阶四边形亚参元分析的PCG 法研究
肖映雄,谢凌洁
(湘潭大学 土木工程与力学学院,湖南 湘潭 411105)
在二维问题有限元分析中,采用四边形网格可以更好地反映变形体中的位移状态和应力状态.为了提高有限元计算精度,往往需要采用相应的高阶单元.这类单元因具有某些特殊的优点,例如,能解决弹性问题的闭锁现象(Poisson’s ratio locking),使其在实际计算中被广泛使用.但与线性元相比,高阶单元节点数多,单元分析复杂,相应离散化矩阵又具有病态性,利用通常的方法[1]求解有限元方程时其效率将大大降低.实际计算时,为了减少计算量,提高编程和计算效率,需要考虑采用阶谱单元技术[2-4],它在生成高阶单元特性矩阵时能够承袭低阶单元的特性矩阵.最近,文献[5]通过适当增加棱内“虚节点”和面内“虚节点”的方式设计了一类四边形升阶谱单元,并结合矩阵的一维稀疏存储技术(CSR 格式)实现了相应的分层四边形高阶亚参元方法.
为了提高这种分层有限元分析的整体效率,需要为其提供高效求解器(Solvers).代数多重网格(Algebraic MultiGrid,AMG)法是求解大规模有限元离散化线性系统最为有效的代数方法之一[6-9].在解决实际问题时,如果还能利用易于获取的某些几何或分析信息,如节点坐标、单元阶次及微分方程的类型等,则可设计出具有更好计算效率的AMG(简记GAMG)法[10-12].文献[13]针对椭圆型定解问题,建立和分析了二次四边形有限元方程的GAMG 法,但该方法需借助于节点基函数的紧支集性和能量极小来建立一系列代数判据,导致求解效率降低.对弹性力学问题,相应的GAMG 法研究也取得了很多成果[14-15].最近,文献[16]针对混凝土随机骨料模型的三角形分层二次元离散化系统,设计了2 种简单有效的预条件子,相应预条件共轭梯度(Preconditioned Conjugate Gradient,PCG)法具有很好的计算效率.
本文针对分层四边形高阶元离散化系统,通过利用其系数矩阵对角分块矩阵的代数性质和分层结构特性,设计了一种简单、有效的预条件子,获得了一种内迭代效率得到显著改善的PCG 法,从而提高了相应有限元分析的整体计算效率.所采用方法的基本思想是将分层高阶元离散化系统本质性地化归为Q4元离散化系统的快速求解,而对Q4元系统,目前已有很多高效的求解器,如GAMG 法.最后,通过对几类实际问题分层Q8元和分层Q12元离散化系统进行求解,验证了方法的有效性.
1 分层高阶四边形亚参元法
在实际四边形有限元分析中,为了提高有限元解精度,需要增加单元插值函数的次数.本节简单介绍文献[5]中通过适当增加棱内“虚节点”和面内“虚节点”方式设计的四边形升阶谱单元及其阶谱函数.
考虑如图1 左图所示的四边形单元.为叙述方便,不妨设Q4单元的四个顶点分别为当由Q4元升阶为Q8元时,需要分别在4 条棱内增加一个虚节点,记为依次下去,当Q8元升阶为Q12元时,需要分别在4 条棱内再增加一个虚节点,当由Q12元升阶为Q17元时,需要分别在4 条棱内再增加一个虚节点,在面内增加一个虚节点当由Q17元升阶为Q22元时,需要分别在4 条棱内再增加一个虚节点,需要在面内再增加一个虚节点这样,该单元当由Q4元升阶为Q22元时,在四条棱内增加的虚节点分别为面内增加的虚节点分别为如图1 中的左图所示,其对应的基本单元如右图所示.更高一阶单元新增棱内“虚节点”和面内“虚节点”均可类似得到.
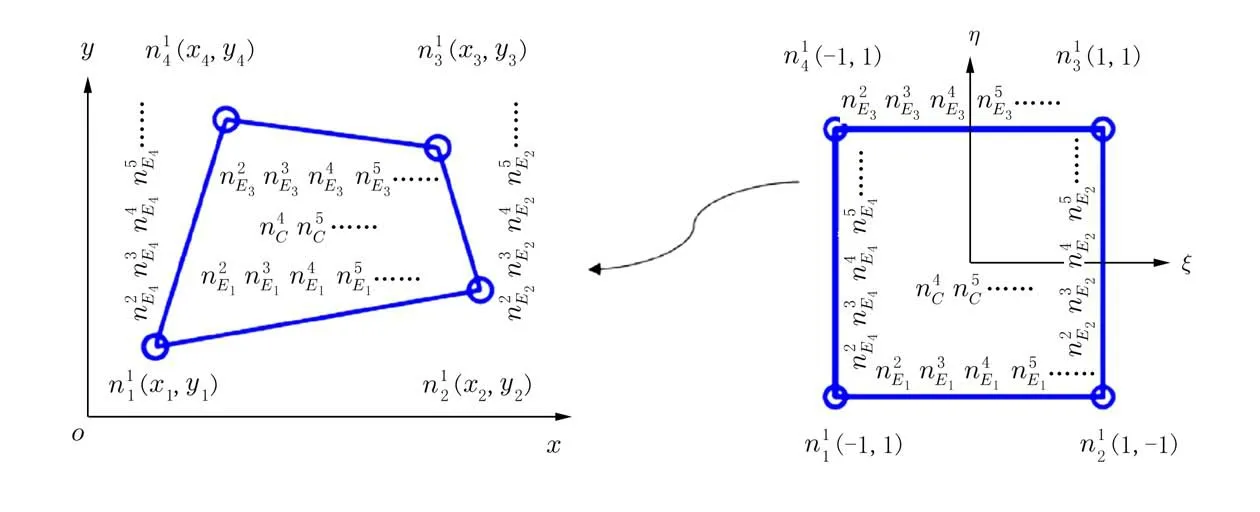
图1 任意四边形单元及对应的基本单元Fig.1 An arbitrary quadrilateral element and the corresponding basic element
设最终升阶后该单元的节点总数为Nn个,采用阶谱单元(Hierachical element)进行分析.二维四边形阶谱单元的形函数包括顶点形函数、虚节点(棱内点和面内点)形函数,利用其性质可在基本单元上构造阶谱函数,列出结果如下:
(1)顶点(p=1),这里,p为相应插值函数中完全多项式的最高次数,对应的阶谱函数即为形函数:
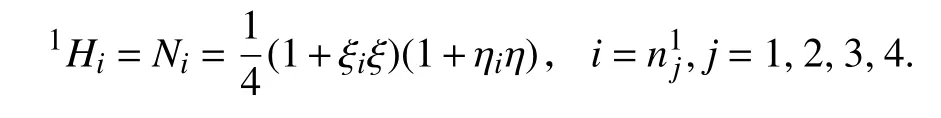
其中,(ξi,ηi)为i点在基本单元中的坐标.
(2)棱内虚节点(p≥2),对应的阶谱函数分别为:
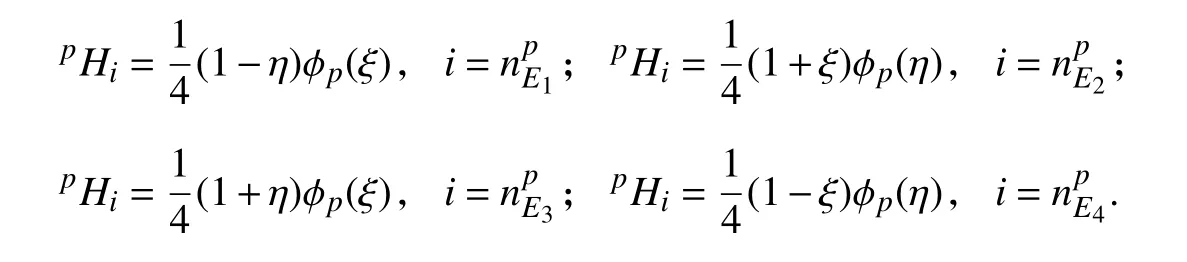
(3)面内虚节点(p≥4),对应的阶谱函数分别为:
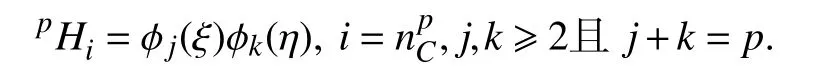
上述各式中,ϕt为一维阶谱单元中可行的阶谱基函数,其形式不唯一.一种常用取法为
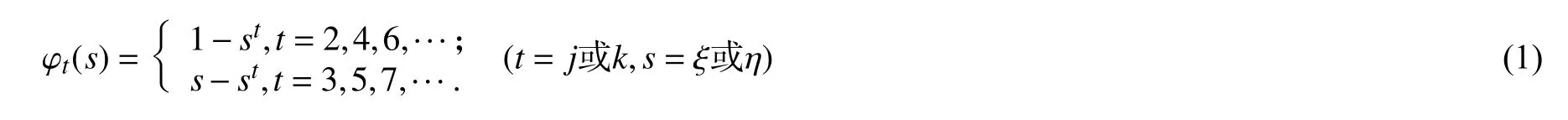
为了程序设计及叙述方便,我们将按以下顺序对各节点进行编号:
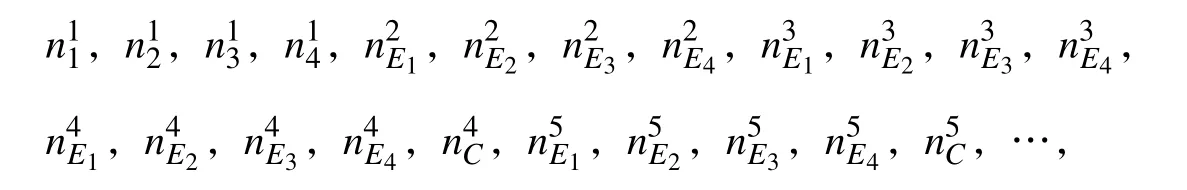
相应的阶谱函数简记为Hi,i=1,2,···,Nn.采用亚参元法进行分析,即单元位移函数采用的变换为

而坐标的插值采用变换:

设Q4元的单元刚度矩阵为

其中,Kij为2×2矩阵,i,j=1,2,3,4.
当Q4元升阶为Q8元时,相应的单元刚度矩阵为


在生成高阶单元刚度矩阵时始终能够承袭低阶单元的刚度矩阵,这样可减少计算量,大大提高编程和计算效率.按照通常等参元法将各单元刚度矩阵进行组集,可得到如下具有分层结构的整体刚度矩阵:

完全类似地,可得到具有分层结构的整体载荷向量FH,(p).最后,引入位移边界条件,修改整体刚度矩阵和整体载荷向量,可得相应的整体刚度方程分层有限元离散系统

其中,dH,(p)为分层p次四边形单元位移向量.上述方程组(7)又可写为


采用高阶“阶谱单元”亚参元分析的优点之一,是它可以为相应的分层有限元离散系统(7)或(8)设计快速求解方法带来更大方便,以提高相应有限元分析的整体计算效率.
2 分层有限元离散系统的PCG 法
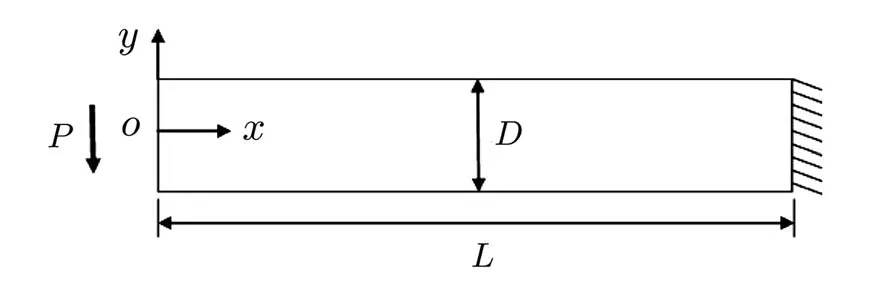
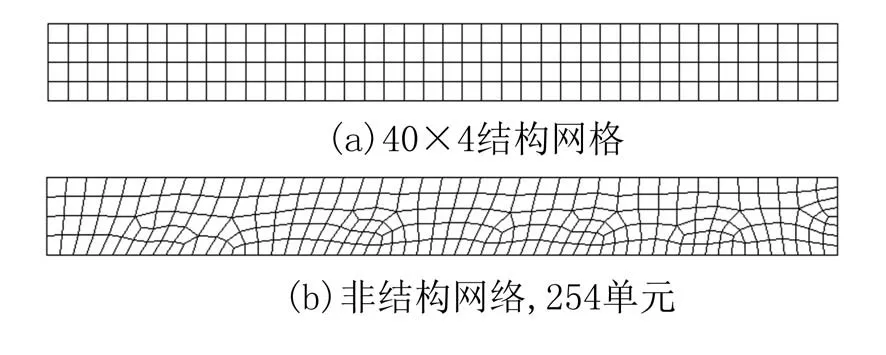
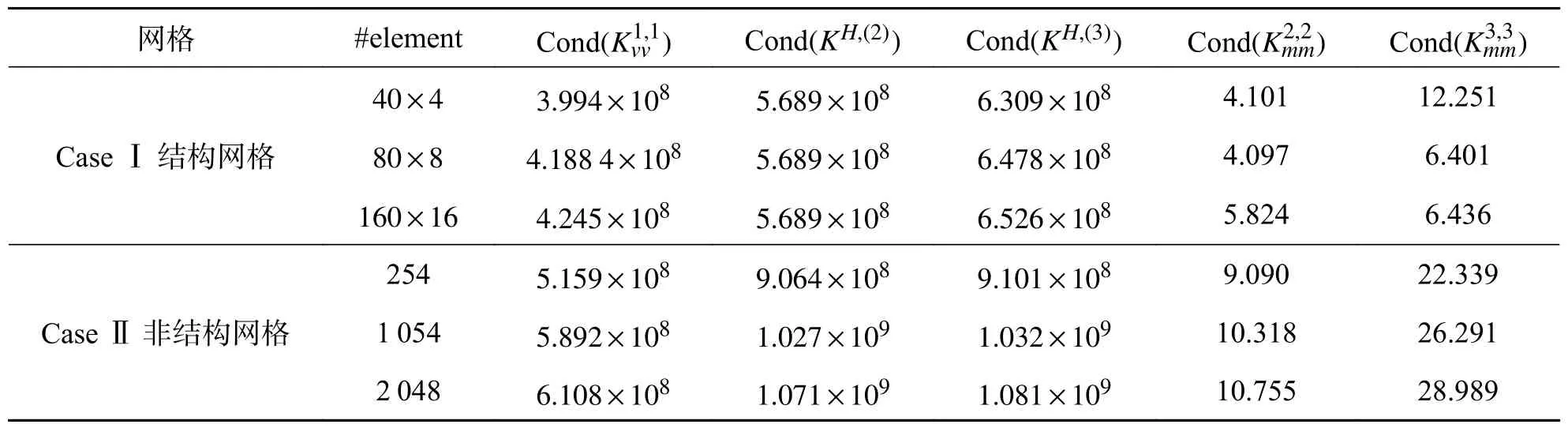
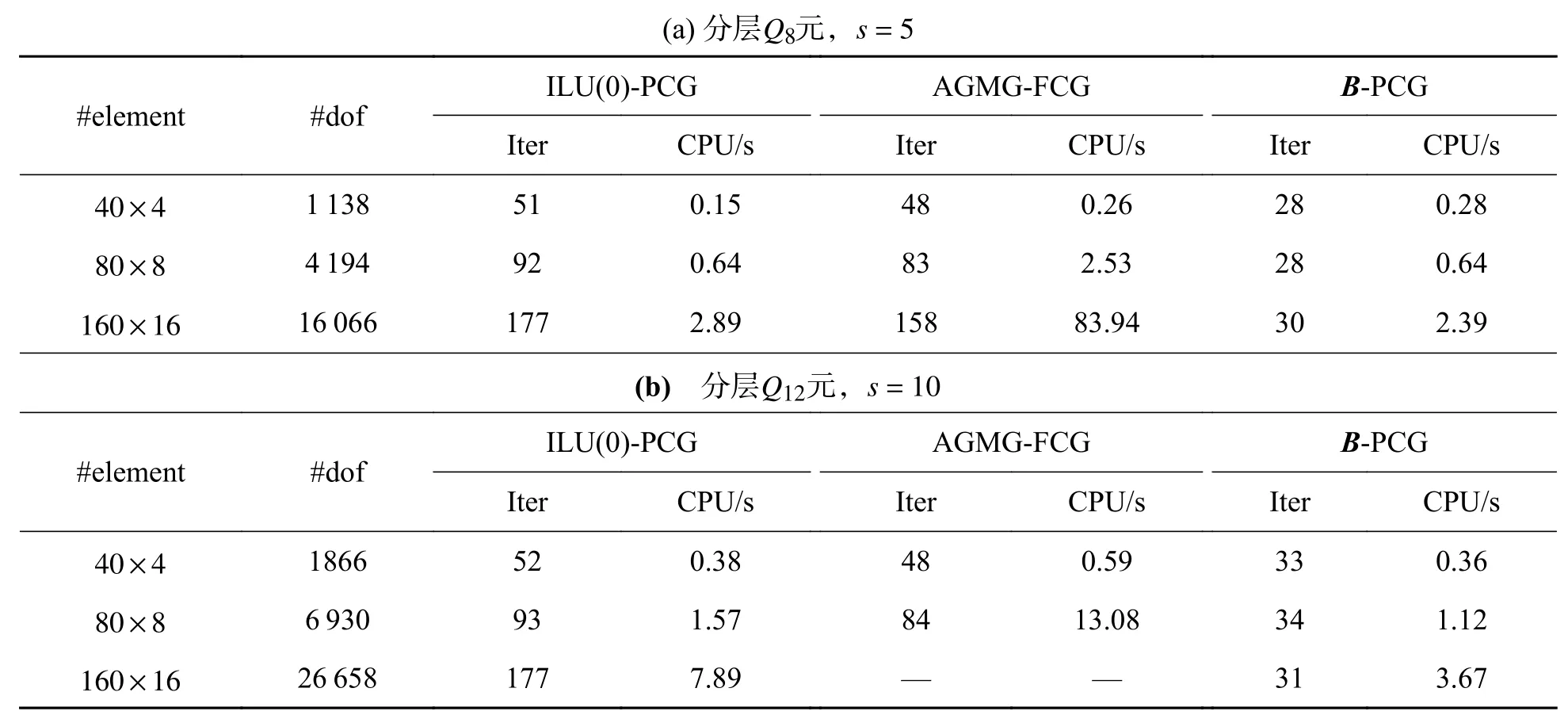
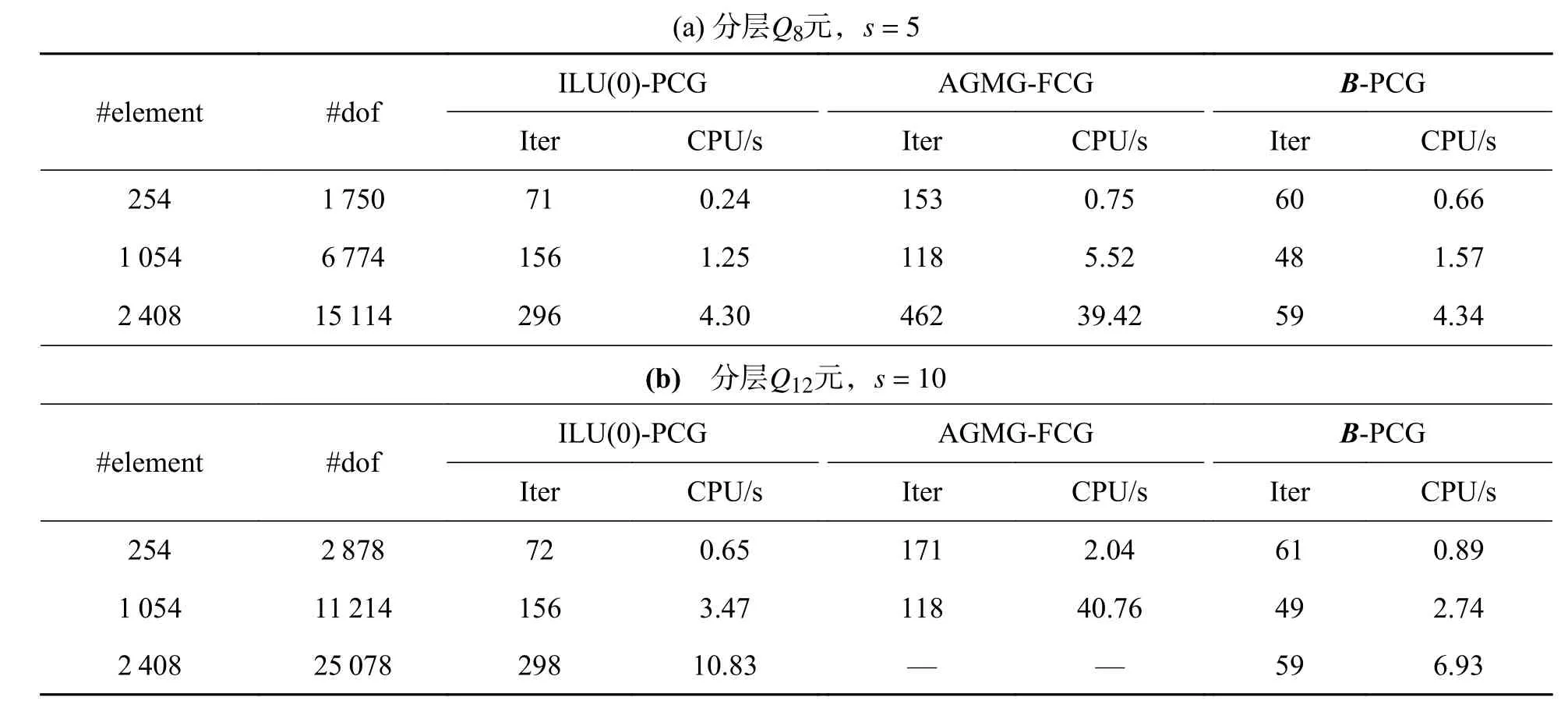
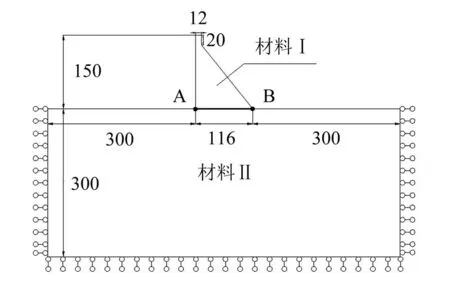
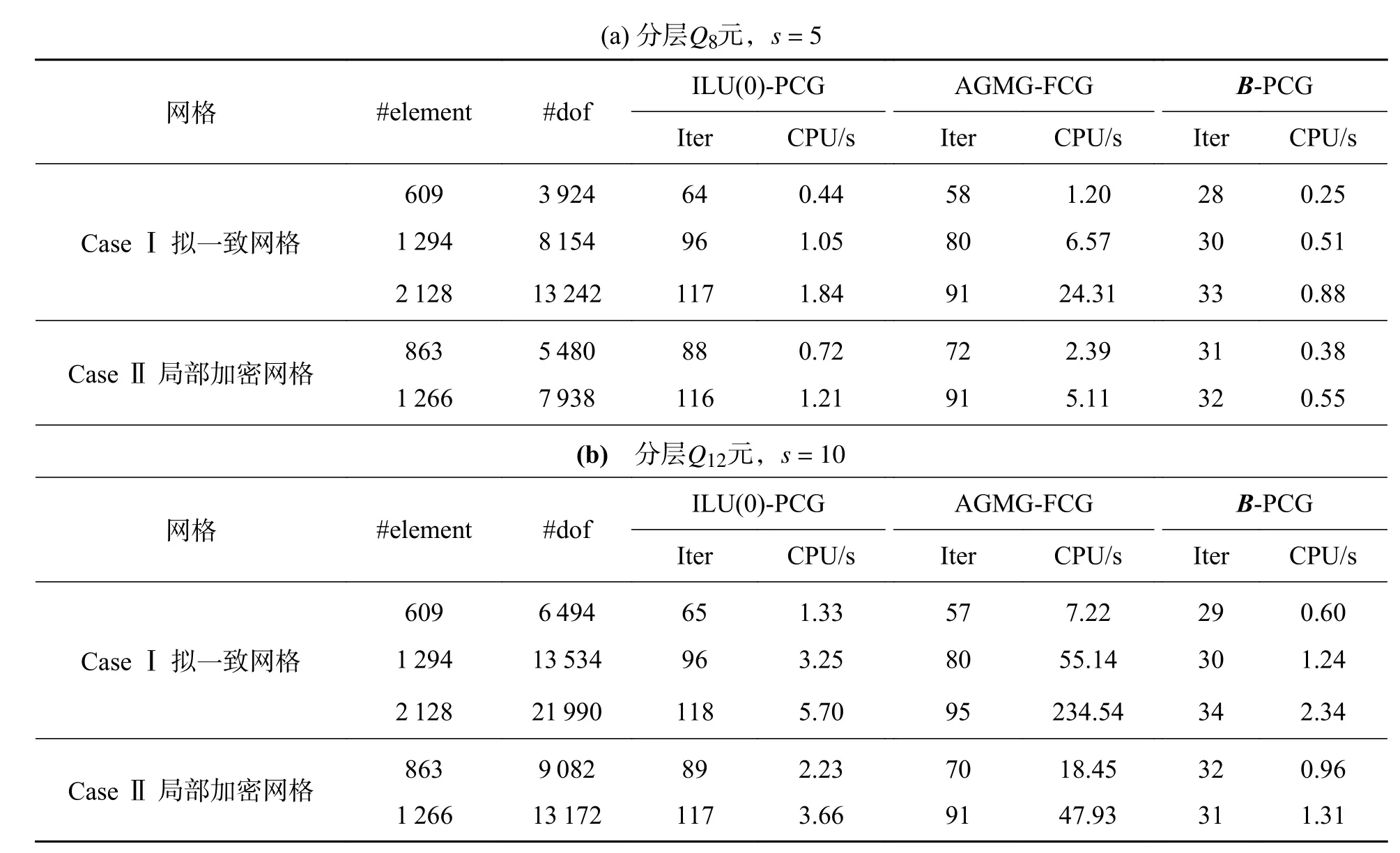
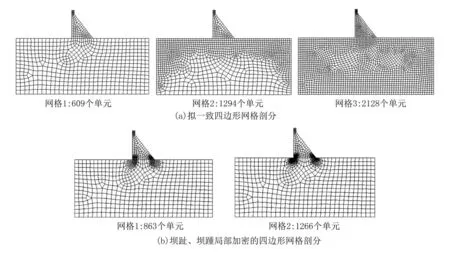
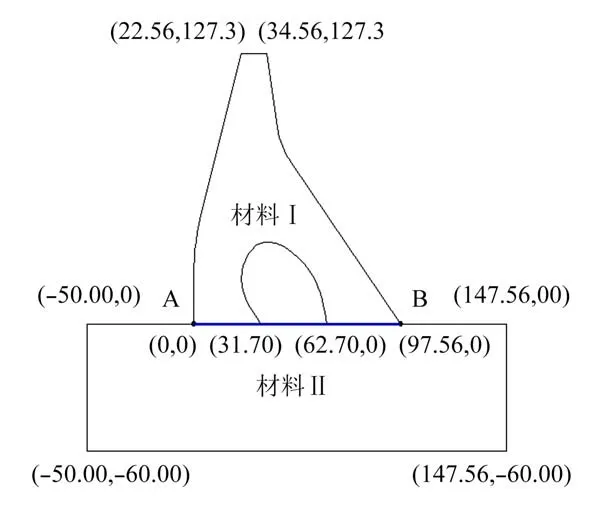
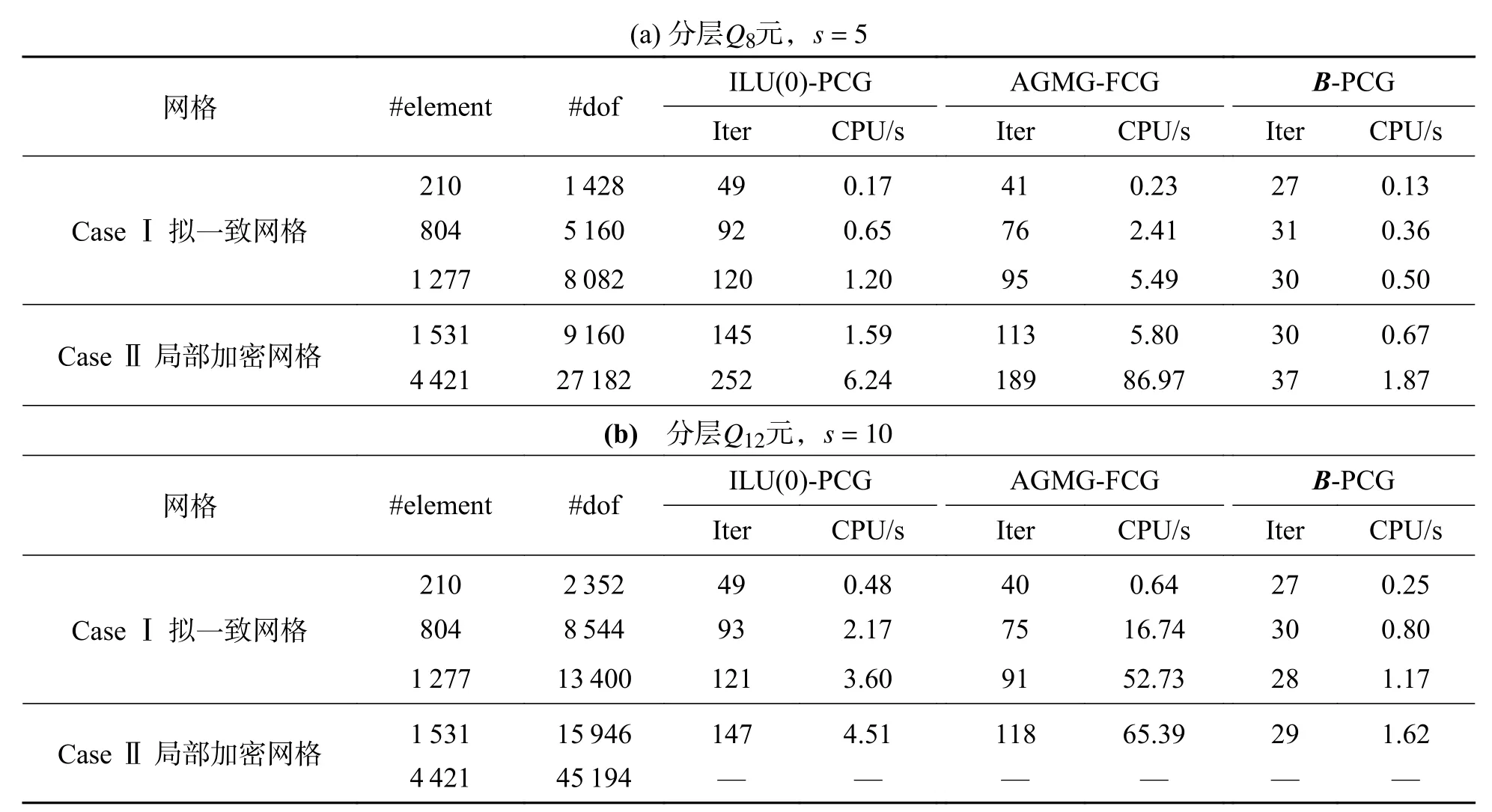
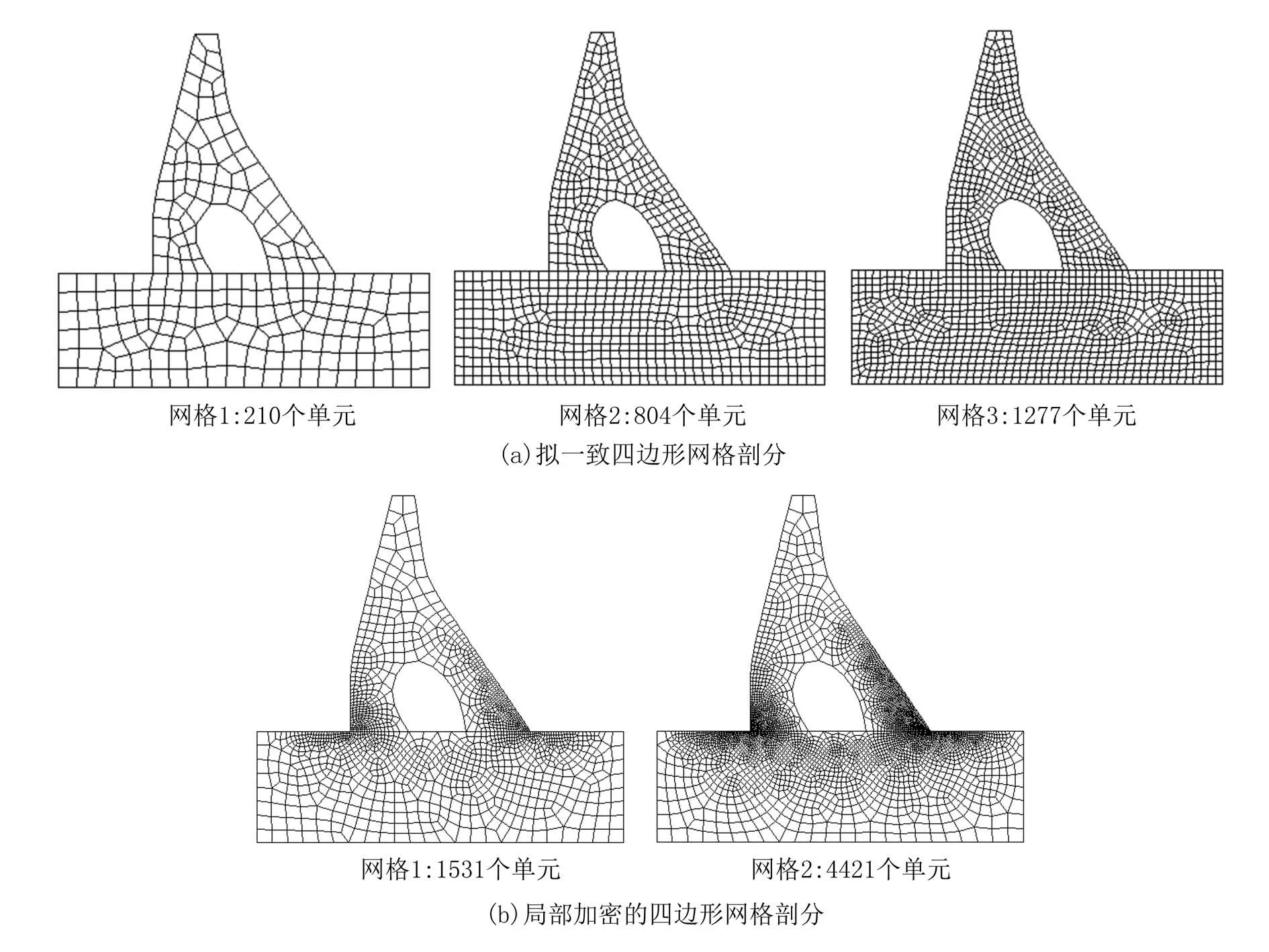
2.1 预条件子的构造分层有限元方程(7)的系数矩阵KH,(p)是对称正定的,在求解该线性代数系统时常常采用预条件共轭梯度(PCG)法.设预条件子为BH,(p),在PCG 算法中,最为关键的环节是给出z=BH,(p)r的快速计算方法,其中,r为给定的已知向量.一般而言,可从两个方面判别一个预条件子是不是一个好的预条件子:首先,BH,(p)r的计算复杂性是否远低于 (KH,(p))−1r;其次,Cond(BH,(p)KH,(p))< 下面,基于文献[16]中算法构造思想,将基于标量椭圆型问题AMG 的块对角预条件子应用于分层有限元离散系统(7)的求解.利用系数矩阵KH,(p)的分层结构特性,不妨取 即可获得相应整体插值算子,记为Pvv,再利用Galerkin方法构造下一个粗网格系数矩阵,即 然后,考虑(11)式中的第二个方程:Kmmzm=rm.通过计算条件数(参看后面的计算结果)可知矩阵Kmm是一个良态矩阵,因此,可直接调用共轭梯度(CG)法近似求解Kmmzm=rm,并设其解为,对应的预条件子简记为 相应的z=BH,(p)r的计算方法总结如下: 算法(计算z=BH,(p)r) 步骤1由Q4元矩阵Kvv得到对角子块,分别基于,并结合经典RS 粗化算法,获取GAMG 法所需的各网格层要素:插值算子与限制算子,粗网格矩阵,再通过选取合适的光滑算子,如Gauss-Seidel 迭代,建立GAMG 迭代方法; 步骤2给定初始迭代向量,调用一次GAMG 法求解Kvvzv=rv,近似解设为; 步骤3给定初始迭代值向量,调用s次CG 法求解Kmmzm=rm,近似解设为; 步骤4取,可得z=BH,(p)r≈. 注1本文所构造的预条件子,充分利用了分层高阶四边形亚参元分析中总刚度矩阵的分块结构特征,将预条件子的计算非常自然地转化为2 个解耦后的子系统的近似求解,这样可分别利用这些子系统矩阵的代数性质(例如,由所有“虚节点”构成的子矩阵的条件数不是很大,为标准的良态矩阵)来选取高效求解方法,以提高PCG 内迭代的计算效率. 2.2 算例及结果分析将基于上述预条件子的PCG(简记为B-PCG)法应用于几类典型问题分层高阶元离散系统(7)的求解,以验证算法的有效性和鲁棒性.在PCG 法中,控制精度取为ε=10−6.本文所有数值实验均在Inter(R) Xeon(R)CPU E3-1230V6 处理器的Windows 10环境下进行. 算例1(悬臂梁问题) 考虑如图2 所示的端部受剪力作用悬臂梁的弯曲问题.设其长为L=10 m,高为D=1 m,取单位厚度,弹性模量E=2.1×106Pa,泊松比ν=0.167,左端(x=0)剪 力P=1 000 N/m,不考虑自重.对区域分别进行结构和非结构四边形网格剖分,图3 分别给出了其中2 种不同类型的网格剖分样图. 图2 端部受剪力作用的悬臂梁Fig.2 Cantilever beam with shear force at the end 图3 2 种不同形式及规模的网格剖分样图Fig.3 Two samples of mesh with different types and sizes 首先,我们在上述2 类网格下计算了相应的分层刚度矩阵KH,(p)及其2 对角块矩阵的条件数,其中,p=2,3.总结如表1 所示,这里,Cond(A)表示给定矩阵A的 条件数,它可表述为,这里,λmax(A) 和λmin(A)分别为矩阵A的最大和最小特征值,A=KH,(p),p=2,3. 表1 分层刚度矩阵KH,(p)及其分块矩阵的条件数(p=2,3)Tab.1 Condition number of the matrices KH,(p),where p=2,3 表1 分层刚度矩阵KH,(p)及其分块矩阵的条件数(p=2,3)Tab.1 Condition number of the matrices KH,(p),where p=2,3 由此可见,对于分层高阶元离散化矩阵KH,(p),其条件数基本不随网格规模及单元阶次的增加而变化,但仍为病态矩阵.对于KH,(p)的两个块对角矩阵,一方面,由各单元顶点组成的Q4元矩阵虽然仍是病态矩阵,但对应条件数比KH,(p)的条件数要小得多,可利用已有的高效方法如GAMG 法进行求解;另一方面,由棱内“虚节点”和面内“虚节点”组成的矩阵则为一良态矩阵,其条件数基本不依赖于网格规模. 然后,将上述PCG 法应用于不同网格规模下悬臂梁问题分层Q8元和分层Q12元离散系统(7)的求解.为了说明本文方法的优越性,将利用工程中应用非常广泛的ILU(0)-PCG[19]和AGMG-FCG[20]进行对比实验,相应的数值试验结果总结如表2 和表3 所示,其中,“#element”表示单元数,“#dof”表示未知数总数,“Iter”表示迭代次数,“CPU/s”表示计算CPU 时间(单位为s). 表2 几种PCG 法求解结构网格下悬臂梁问题的迭代次数和计算CPU 时间Tab.2 Iteration counts and CPU time of several PCG methods for cantilever beam on structured meshes 表3 几种PCG 法求解非结构网格下悬臂梁问题的迭代次数和计算CPU 时间Tab.3 Iteration counts and CPU time of several PCG methods for cantilever beam on unstructured meshes 注2对悬臂梁问题,程序中采用的AMG 粗化算法在所有自由边界上不是标准粗化,在这些节点上所构造的插值算子不能重构刚体模式(rigid body modes),将会导致GAMG 法的收敛速度受到影响.因此,在实施算法中的步骤2 时,改为调用5 次GAMG法近似求解Q4元 离散系统Kvvzv=rv,以提高PCG法内迭代计算效率.在程序实现时,我们先将GAMG 迭代所需的各个要素一次性生成并保存好,所以整个迭代时间仍是很快的. 算例2(重力坝问题) 考虑某重力坝问题,其计算断面尺寸如图4 所示,作为平面应变问题进行有限元分析.假设坝体和坝基均为线弹性材料,其中,坝体的材料常数为E=20 GPa和 ν=0.167,密度为 γ=2 400 kg/m3,坝基的材料常数为E=20 GPa和 ν=0.25.边界条件如图4 所示,假设水位与坝顶齐平,计算时只考虑坝体自重和上游水压力. 图4 某重力坝截面尺寸及边界约束(单位:m)Fig.4 Section sizes of a gravity dam and the boundary conditions (unit: m) 对区域进行非结构四边形网格剖分,图5 分别给出了2 类不同类型及规模的网格剖分图.将上述PCG 法应用于不同网格规模下重力坝问题分层Q8元 和分层Q12元离散系统(7)的求解,相应的数值试验结果总结如表4 所示. 表4 几种PCG 法求解重力坝问题的迭代次数和计算CPU 时间Tab.4 Iteration counts and CPU time of several PCG methods for the gravity dam 图5 2 类不同类型的重力坝网格剖分图Fig.5 Two types of unstructured meshes with different elements for the gravity dam 算例3(腹拱坝问题) 考虑如图6 所示的腹拱坝,其中坝体和坝基均采用线弹性模型,坝体的弹性常数为E=23 GPa 和v=0.17,密度为2 400 kg/m3,坝基的弹性常数为E=15 GPa 和v=0.17,坝基底部为纵向约束,两侧均为横向约束.设上游水平面与坝顶齐平,计算时只考虑坝体自重和上游对坝体的水压. 图6 腹拱坝截面尺寸(单位:m)Fig.6 Section sizes of the arch-abdomen dam (unit: m) 对区域分别进行非结构拟一致四边形网格剖分和局部加密四边形网格剖分,图7 分别给出了不同规模的两类网格剖分图.两种PCG 法求解不同网格规模下腹拱坝问题分层Q8元 和分层Q12元离散系统(7)的数值结果总结如表5 所示. 表5 几种PCG 法求解腹拱坝问题的迭代次数和计算CPU 时间Tab.5 Iteration counts and CPU time of several PCG methods for the arch-abdomen dam 图7 2 类不同类型的腹拱坝网格剖分图Fig.7 Two types of unstructured meshes with different elements for the arch-abdomen dam 由上述数值结果可见,我们设计的B-PCG 法对求解分层Q8元 和Q12元离散化系统均具有很好的计算效率和鲁棒性,且随着单元阶次的增加和问题规模的不断增加,B-PCG 法的优势更明显.例如,对腹拱坝问题,当单元数为1 277 时,3 种方法求解分层Q8元离散系统的迭代次数和计算CPU 时间分别为:ILU(0)-PCG 法为120 次和1.20 s,AGMG-FCG 法为95 次和5.49 s,而B-PCG 法仅为30 次和0.50 s;求解分层Q12元离散系统的迭代次数和计算CPU 时间分别为:ILU(0)-PCG 法为121 次和3.60 s,AGMG-FCG 法为91 次和52.74 s,而B-PCG 法仅为28 次和1.17 s.在设计两水平PCG 法时,由于采用了分层有限元,不需构造网格转换算子和线性元矩阵.由于Kvv在PCG算法调用中保持不变,将基于Kvv的GAMG 法所需的各网格层信息,包括网格转移算子、粗网格系数矩阵等一次性生成好,再充分利用GAMG 法在求解非结构网格下Q4元离散系统所具的优势,能够显著提高内迭代的计算效率以及相应PCG 法的迭代效率. 四边形高阶单元是能有效提升二维问题有限元分析计算精度的一类常用单元.实际应用时,可通过适当增加虚节点的方式增加单元形函数的次数,从而提高有限元近似解的计算精度.这些虚节点仅要求设置在棱内部或面内部即可,不需要具体的几何坐标,处理非常灵活,相应的阶谱函数也易于构造,且其对应的有限元矩阵具有分层结构特性,易于为相应离散代数化系统的求解设计高效求解器. 本文通过利用分层高阶四边形元离散矩阵的分层结构特性及分块对角矩阵的性质,为相应离散系统的求解提供了一种简单有效的预条件子,所得到的两水平分层PCG 法具有很好的计算效率.这种预条件子的构造是通过将高次元离散系统方程的求解本质性地化归为Q4元离散系统的求解,再利用现有的高效GAMG 法求解Q4元离散系统,即可获得内迭代计算效率得到显著提高的PCG 法.本文方法也可以推广应用于三维问题及非线性有限元数值计算中,或者其它实际工程计算问题的数值模拟中,以提高相应有限元分析的整体效率.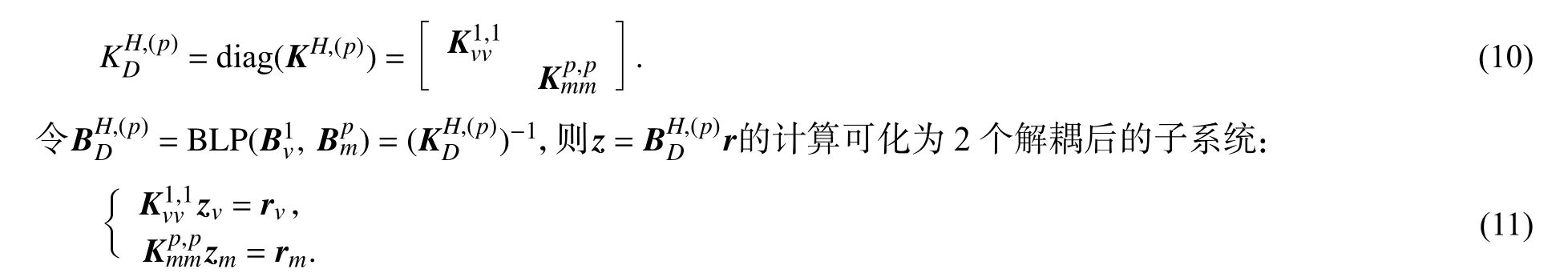



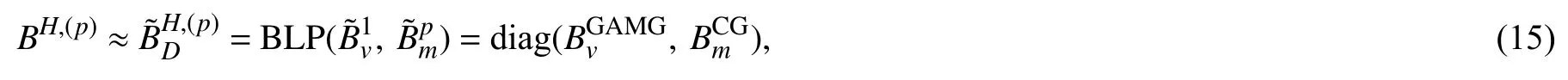
3 结语

