ISGW 有效相对介电常数的提取研究

陈剑培，申东娅

(1.云南大学 信息学院，云南 昆明 650500；2.云南民族大学 电气信息工程学院，云南 昆明 650500)

人工智能、物联网等技术的发展对未来6G 通信提出了更高的挑战，通信数据速率要求达到100 Gb/s 以上，能量效率比5G 提高100 倍以上，以实现通信高精度定位、高速移动、超大接入容量和超高可靠性等[1-2].作为未来通信系统的硬件基础，集成电路面临着高速度、低损耗、多功能的重大挑战，传统的传输线如微带线、带状线、金属矩形波导等，已无法满足未来通信系统的要求.微带线在毫米波电路中将产生更多的辐射波和表面波，而传统矩形波导虽然损耗低，但体积大、难集成.集成基片间隙波导（Integrated Substrate Gap Waveguide，ISGW）采用电路印刷板技术，利用3 层介质基板实现了对微带线的封装，降低了毫米波电路中的微带线辐射损耗，且容易电路集成，可以实现与其它微带电路的直接连接[3-4].

Shen 团队已经将ISGW 应用于毫米波器件研究[5-12].由于ISGW 的自封装特性，团队研究的ISGW 磁电偶极子天线、ISGW 缝隙天线、ISGW圆极化天线的单天线增益均在8 dB 以上，远远高于其他类型天线的增益性能[6-9].ISGW 滤波器同样具有很大的优势，其滤波耦合拓扑由于ISGW 的微带脊布线灵活而得到了双传输零点特性，提高了滤波器的性能[10-11].

作为非均匀介质传输线，有效相对介电常数可以计算ISGW 的电磁波波长，是滤波器、天线等电路设计的关键参数，但目前还没有ISGW 的有效相对介电常数理论可遵循.在ISGW 电路设计的文献中，电磁波波长的计算方法主要采用微带线有效相对介电常数理论进行估计或仿真软件ANSYS 反复实验获取[5-8].利用仿真软件ANSYS 对ISGW 进行建模仿真可以得到介电常数epsilon，该数据是ISGW 导带所处的上下两层介质板的相对介电常数综合，未考虑第三次层介电常数影响，存在着很大的误差.

介电常数作为重要的微波参数，与传输线的介质板材质、工作频率有关[13].电路在均匀介质中时，传输电磁波的波长可以通过均匀介质的相对介电常数计算[14]；而在非均匀介质中，波长则无法直接由介质板的相对介电常数获得，需要通过其他方法计算.如微带线属于一种简单的非均匀介质传输线，单层介质板结构中导带一侧是介质板，另一侧是空气，其工作波长通过有效相对介电常数计算.Sharma 已给出多种工作频段、多种介质板下，有效相对介电常数和介质板相对介电常数、介质板厚度和导带宽度的关系表达式，准确率较高[15].

传输线的介电常数可通过加工传输线模型、测量模型的频率特性得到.对于均匀介质，利用测量均匀介质的频率谐振特性计算相对介电常数，如谐振腔法[16]、开路微带线谐振法[17]、环形微带谐振法[18]等，方法简单.而对于超薄材料，基于开路谐振法的扰动法可以得到比较准确的介电常数[19]；基于反射系数和散射系数的同轴探头夹具系统，可以测量平面传输线介电常数测量[20]，方法准确，但只能对均匀介质进行计算；非均匀介质传输线的有效相对介电常数测量和计算非常困难，刘宏梅等总结了电路板介电常数的时域测量法，并提出开路微带线夹具测量的方法来计算非均匀介质传输线有效相对介电常数，但要以相同长度微带线的有效介电常数作为参考，带来了由于数据比对的计算误差[21].

本文针对ISGW 提出一种从反射系数S11数据中提取有效相对介电常数的半波长法.首先对ISGW 的结构和工作原理进行阐述；接着提出了半波长法来提取有效相对介电常数；最后对ISGW 模型进行仿真和有效相对介电常数提取，并与ANSYS软件中的仿真结果进行比较，证明了该方法的适用性.

1 ISGW 工作原理

ISGW 的结构和参数如图1 所示.图1（a）是ISGW 的三维视图，ISGW 由3 层介质基板组成，上层介质板的上表面为金属敷铜，下表面以微带脊作为导体，中层介质板的厚度小于工作波长的1/4，下层介质板是由电磁带隙结构（Electromagnetic Band Gap,EBG）和下表面金属敷铜构成.图1（b）是ISGW 的俯视图，标注了ISGW 的长度L、宽度Wi、微带脊的宽度为w和EBG的参数.图1（c）是ISGW 的侧视图，标注了3 层介质基板的相对介电常数 εr1、εr2、εr3和 高度h1、h2、h3.

电磁波沿着ISGW 的微带脊传输.周期性排列的EBG 作为人工磁导体结构，对微带脊传输的电磁波具有抑制作用，使电磁波只能沿着微带脊传播，防止能量向两边泄漏.ISGW 的中间层非常薄，使微带脊与EBG 分离，便于电路布线设计.

为了研究ISGW 的传播特性，我们建立了一个ISGW 模型，3 层介质板都采用罗杰斯公司Rogers-RT5880 的介质基板，相对介电常数为εr1=εr2=εr3=2.2，ISGW 模型的其他参数、含义和取值如表1 所示.

表1 ISGW 模型的参数Tab.1 Parameters of ISGW model

ISGW 的工作频段由周期性排列EBG 的禁带频率范围决定.首先利用ANSYS 仿真软件得到了EBG 的色散图，如图2 所示.图2 中给出了EBG 的两个传输模式Mode 1 和Mode 2 的传播传输频率特性，而在频率范围23.3～ 42.2 GHz 内无传播模式存在，即为EBG 的禁带范围.接着仿真了ISGW 的传输特性，包括散射参数S11和 传输参数S12，如图3所示，可以看出工作频段（S11<−10 dB 且S12>−3 dB）为25～45 GHz，几乎与EBG 的禁带重叠，且工作频段内传输参数S12的平均值为0.6 dB.而且，从图3 左下角ISGW 在32 GHz 处的电场分布可以看到，电场中心位于ISGW 的微带脊上，没有向两侧泄露，实现了平面电路的封装.

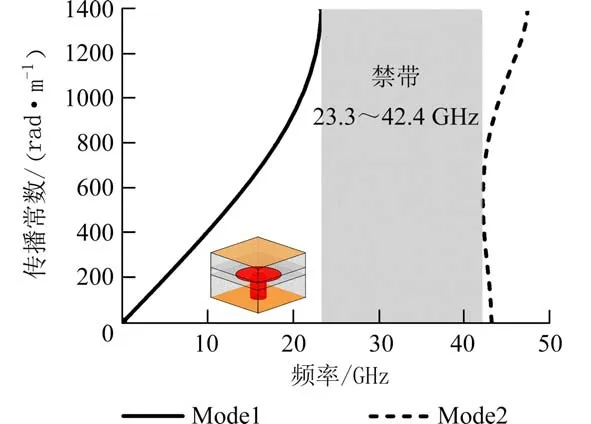
图2 EBG 的色散图Fig.2 Dispersion characteristics of EBG

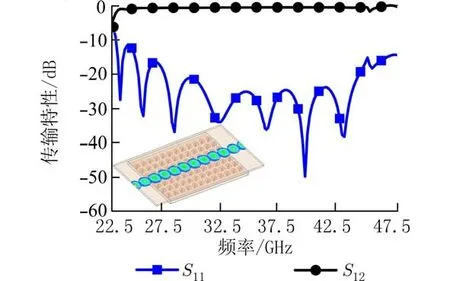
图3 ISGW 的S 参数及电场Fig.3 S-parameters and electric field of ISGW

ISGW 3 层介质板的相对介电常数可以相同，也可以不同，在图1 的ISGW 模型中3 层介质板的相对介电常数相同，取值为2.2.在ISGW 应用到滤波器、天线等器件设计的全波仿真中，利用相对介电常数 εr=2.2 计算ISGW 工作波长的公式λISGW=并不正确，只能通过参数优化来设计.原因是ISGW 的下层介质板包含了周期性结构EBG，EBG 是具有谐振特性的物理结构，因此，ISGW 的相对介电常数不能作为计算ISGW 工作波长的公式，应该修正为：

式中，λISGW是 ISGW 传播波长，c 是光速，f是工作频率，εe是ISGW 的有效相对介电常数.

在3 层介质板相同的ISGW 模型的工作频段内，EBG 对电磁波传输起到人工磁导体或者高阻抗表面的作用，可以在ISGW 的工作频段内等效为开路的电路模型.根据电动力学中利用分布电容计算相对介电常数的理论，由于3 层介质板的相对介电常数都为2.2，ISGW 的有效相对介电常数应该小于2.2；如果3 层介质板的相对介电常数不相同，ISGW 的有效相对介电常数应该小于ISGW 结构去掉EBG 后带状线的有效相对介电常数.

2 半波长法

半波长法是从ISGW 的S11结果中提取特定频率的有效相对介电常数.在这些频率下，ISGW 的长度是传播电磁波的半波长的整数倍，ISGW 的输入阻抗与负载阻抗相等.

对于长度为L的ISGW 模型，其输入阻抗Zin是L的函数，与负载阻抗ZL之间满足关系式：

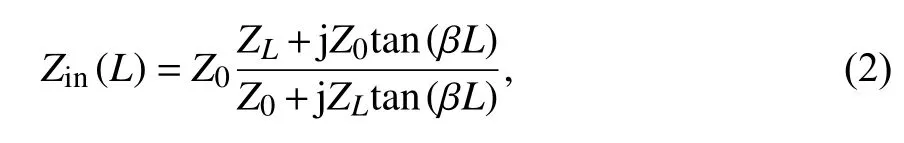
式中，Z0是ISGW 的特性阻抗，β是传播常数，可表示为 β=2π/λISGW.

在某些特定的工作频率fi（i=1，2，···）处，ISGW 的长度L是将频率fi代入式（1），求出的半波长的整数倍，表示为：

式中，n为一个实整数.将式（3）代入式（1），可以得到输入阻抗为：

此时，输入阻抗等于负载阻抗，且与ISGW 的特性阻抗Z0无关.对于ISGW 的反射系数S11，会在频率fi处出现一个极小值点.综合式（2）和式（3），提取ISGW 有效相对介电常数的表达式为：

以上是半波长法提取有效相对介电常数的原理.现在讨论n的取值，如果ISGW 的工作频段从0 GHz 开始，当fi=0 GHz 时，n=0，S11会出现一个极小值点.但是，ISGW 受到EBG 禁带的影响，其工作频段不是从0 GHz 开始，而是从某个频率开始，因此n也是从非零开始取值.

3 提取有效相对介电常数

基于半波长方法对上节的ISGW 模型进行了仿真，其中ISGW 的长度L=19.8 mm.从仿真S11结果中提取了有效相对介电常数，并与仿真软件中给出的有效相对介电常数结果epsilon 进行比较，验证了该方法的适用性.

3.1 仿真结果及提取使用高频电磁仿真软件ANSYS 对长度L为19.8 mm 的ISGW 模型进行仿真，得到S参数的仿真结果如图4 所示.可以看出，ISGW 的工作频段（S11<−10 dB 且S12>−3 dB）为25～45 GHz.在工作频段内包含了5 个极小值点，为了保证输入阻抗和负载阻抗的最佳匹配，我们选取在S12>−1 dB 情况下的4 个极小值点.图4 中标注出这4 个极小值点，对应的特定频率fi分别为f1=27.4 GHz、f2=31.7 GHz、f3=36.5 GHz 和f4=41.9 GHz.

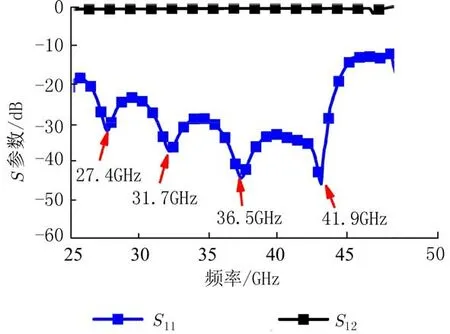
图4 ISGW 的仿真S 参数Fig.4 Simulated S-parameters of ISGW

为了获得ISGW 长度对应于半波长的整数倍n值，我们得到了4 个极小值点频率处的电场图，如图5 所示.在电场图中，通过电场周期性的强弱变化，可以判断出在f1、f2、f3和f4处，ISGW 长度分别对应于半波长的5、6、7 倍和8 倍，即n=5、6、7 和8.

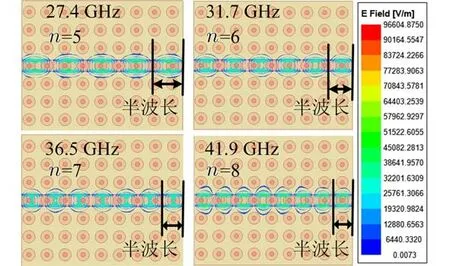
图5 S11的4 个极小值频率处的电场图Fig.5 Electric field at frequencies of four minimums of S11

利用公式（5），我们可以提取出ISGW 的有效相对介电常数，结果如表2 所示.

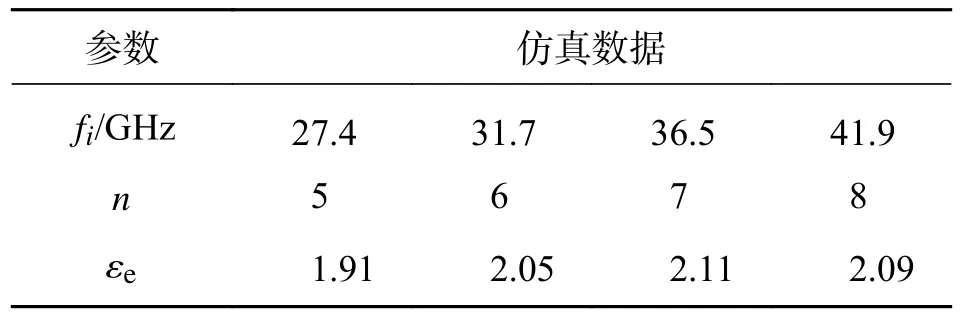
表2 仿真S11中提取的有效相对介电常数Tab.2 Effective relative permittivity extracted from simulated S11

可以看出，提取的有效相对介电常数随着频率的变化而变化，符合介电常数时随频率变化的基础理论，也符合本文对有效相对介电常数和介质板相对介电常数的推论，εe<2.2.

3.2 有效相对介电常数的插值与比较半波长法提取的有效相对介电常数（如表2）只有4 个频点，工作频段内其他频点的有效相对介电常数可以通过插值得到.通过Matlab 软件对数据进行了3 次样条插值，插值范围为ISGW 的工作频段25～45 GHz，插值的结果如图6 中的虚线所示.

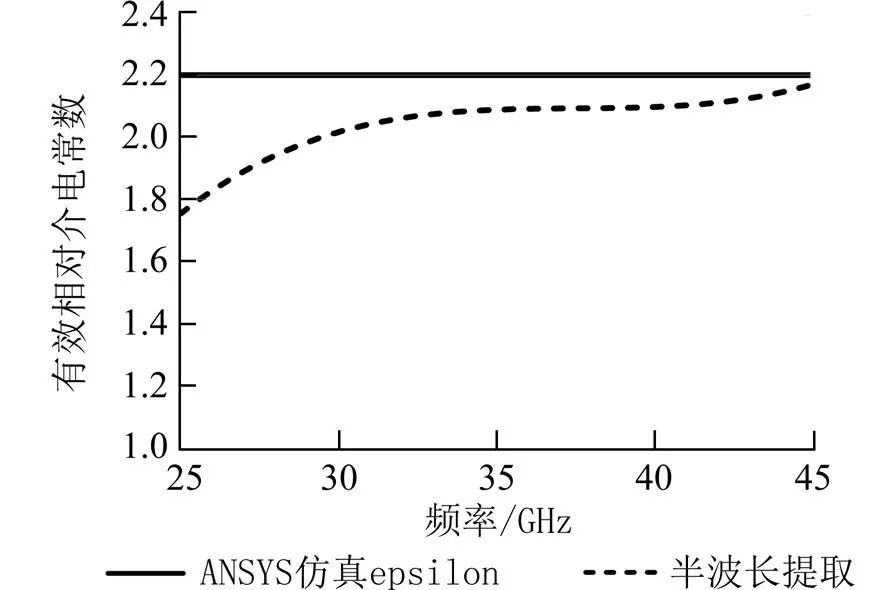
图6 半波长提取的有效相对介电常数与ANSYS 仿真epsilon 结果Fig.6 The relative permittivity extracted by half-wavelength method and epsilon results simulated by ANSYS

利用ANSYS 仿真软件的模式求解和波端口激励方式可以求解ISGW 的有效相对介电常数.本文建立的ISGW 模型的仿真有效相对介电常数结果epsilon 如图6 中的实线所示.与本文提出的半波长法提取的有效相对介电常数结果相比，epsilon取恒定值2.2，不随频率变化.这是因为微带脊的上下介质板的相对介电常数相等（εr1=εr2=2.2），仿真软件仅仅考虑了这两层的电特性，未考虑第三层介质板的EBG 对ISGW 输特性的影响.

为进一步说明ANSYS 仿真数据epsilon 的误差，本文比较了ISGW 3 层介质板不同时的仿真结果.当ISGW 微带脊的上下介质板的相对介电常数不相等时（εr1=2.2、εr2=3.66），ANSYS 仿真ISGW模型的epsilon 结果介于两者之间，随频率变化.该比较结果也证明了对ANSYS 仿真epsilon 数据的分析，ANSYS 软件仅考虑上下介质板两层的电特性，不适合对多层非均匀介质传输线进行仿真.因此，本文利用半波长法提取的有效相对介电常数可以修正ANSYS 的有效相对介电常数仿真结果.

4 结论

本文研究了ISGW 的有效相对介电常数的提取.ISGW 采用3 层介质板，利用EBG 使电磁能量集中在微带脊，不向两侧泄露，实现了电路的自封装，降低了传输线的损耗.首先研究了一个毫米波波段25～45 GHz 的ISGW 模型，提出基于阻抗匹配的半波长方法，当ISGW 模型的长度是半波长的整数倍时，ISGW 的输入阻抗和负载阻抗相等，模型的反射系数S11在工作频段内出现极小值.然后利用半波长法在S11取极小值的频率处提取ISGW的有效相对介电常数，并与电磁仿真软件ANSYS仿真的有效相对介电常数数据进行对比，验证了该方法的适用性，为ISGW 应用研究的工作波长计算提供了简单可行的方案.下一步的工作中我们将采用本文提取的有效相对介电常数计算ISGW 谐振器的工作波长，并进行实验验证.