Y形活塞杆密封动静态性能分析及结构优化

杜家熙 王 正 方 正 郑淏阳 刘刚军

(大连理工大学能源与动力学院，辽宁大连 116000)

液压缸作为液压传动装置中产生高压流体的主要设备，在现代工业的许多领域都起到了重要的作用，而液压缸中活塞杆的密封是保障液压装置和系统正常工作的关键部件[1]。Y形密封因具有静摩擦阻力小、启动平稳、耐压性好等特点而被广泛应用在液压缸的活塞杆往复密封系统中[2]。作为一种接触式动密封，Y形密封依靠往复运动过程中活塞杆与Y形圈之间的密封表面(主密封面)发挥密封作用，因此工作过程中主密封面的接触、润滑与磨损等问题对其密封性能有较大影响。

从20世纪中旬开始，国外学者针对往复密封系统的接触、润滑问题进行了一系列的理论研究[3]。WHITE和DENNY[4]通过实验研究了往复密封在不同压力、速度、温度等条件下的密封性能和失效机制。SALANT、YANG等[5-7]为更加准确地描述密封面上的接触、流动问题，建立了混合润滑理论，并以O形圈为研究对象，计算并试验验证了模型的准确性。近年来，国内的研究人员在这些理论的基础上对成型填料密封进行了许多分析及优化设计工作。黄乐等人[8]利用有限元方法对Y形圈进行分析，提出根部倒角的方法优化其抗挤出性能，并使用正交试验对关键结构参数进行优化，改善了Y形圈的摩擦性能。DONG、廉志刚、孙娟娟等[9-11]先后利用IHL、EHL、TEHL理论研究了摆动马达用组合密封的密封特性。高涵宇[12]利用正交试验方法研究蓄能弹簧密封圈的静密封特性并进行了结构优化，同时利用IHL方法分析了活塞杆速度、工况参数等对动密封性能的影响。

在以往的Y形圈优化设计研究中，优化的对象往往是接触压力、应力、摩擦力等结构力学分析结果，对于直接体现密封系统润滑性能的泄漏量等指标进行优化的研究较少。本文作者针对Y形往复密封系统进行有限元分析计算，并根据往复密封原理计算了不同压力下Y形密封的泄漏特性；使用Design Expert针对Y形密封泵回量进行优化设计，优化后活塞杆密封的动、静密封性能提升，磨损速度及被咬伤的风险下降，提高了密封的可靠性。

1 活塞杆密封原理

活塞杆密封作为一种接触式动密封，其密封性能由密封接触面的润滑状态所决定。在活塞杆往复运动的过程中，液压缸中的黏性流体会被带入密封面，并在密封面上形成较高的液体压力使密封圈与活塞杆间出现一层液压油膜，这就是所谓的动压润滑。通常来说，油膜越薄，密封圈与活塞杆在相对运动过程中接触的概率越大，磨损就越快；相反，较厚的油膜可以保证密封处于良好的润滑状态，延长密封工作寿命，但是密封面上的泄漏量会随之增加。

活塞杆密封在正常工况下存在外行程、内行程2种状态。在外行程中，缸内少量液压油会被拖入密封面中形成外泄；在内行程中，密封面上的液压油又会被泵回缸内，2个行程中流量的差值即是活塞杆密封在一个工作循环中的净泄漏量。外行程中，油膜的厚度、压力、速度分布如图1所示。

图1 活塞杆密封原理示意

密封面间流体的流动遵循一维雷诺方程：

(1)

式中：h为油膜厚度；p为油膜压力;μ为流体黏度；U为活塞杆与密封圈的相对运动速度；x为沿水平方向坐标。

对式(1)积分可得：

(2)

(3)

由式(3)可知，油膜厚度取决于压力梯度分布、活塞杆运动速度及流体黏度。油膜压力p(x)可由有限元求解的静态接触压力近似得到，进而可以得到油膜压力梯度分布。对式(3)取微分得：

(4)

(5)

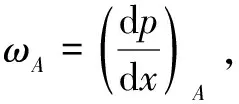
(6)

将式(6)代入式(3)中可得最大油膜压力处的油膜厚度：

(7)

根据动压润滑理论，在最大压力处，油膜的运动速度从uo线性减小至0，其中uo为活塞杆外行程运动速度。在靠近大气一侧，油膜具有均匀的运动速度uo。由于油膜分布具有连续性，在不同位置液体流量相等，因此大气侧油膜厚度是最大压力处油膜厚度的1/2，即：

(8)

同理，在内行程中，当活塞杆运动速度为ui时，假设点E为油膜压力梯度最大值点，则压力最大点的油膜厚度为

(9)

内行程中，界面外的液体侧，油膜具有均匀流速ui，油膜厚度为

(10)

由式(8)、(10)即可确定活塞杆每一往复循环中的净泄漏量[13]：

(11)

式中：d为活塞杆直径；L为活塞杆行程。

从式(11)中可以看出，活塞的泄漏量与活塞杆直径及行程长度成正比，且当括号内的值为0或负值时，活塞杆密封的往复密封性能较好。当密封面内侧接触压力梯度较大时，或内行程速度较大时，密封具有过剩的泵送能力，可以保证密封的可靠性。

综上，Y形圈密封特性计算流程如图2所示。

图2 密封特性计算流程

2 有限元分析模型

2.1 几何模型

GB/T 10108.1—2000《往复运动橡胶密封圈结构尺寸系列 第1部分：单向密封橡胶密封圈》[14]中规定的不等高唇Y形密封结构如图3所示。这种结构具有较好的防咬伤、防翻转的能力，同时对偏心轴具有较好的补偿作用。

图3 Y形密封系统示意

根据上述标准建立二维轴对称几何模型，并在建模时使Y形圈与活塞杆、密封沟槽分别产生初始干涉，以便于模拟过盈状态下密封系统的受力、变形情况。

2.2 材料模型

活塞杆及密封沟槽的材料属性使用线弹性模型进行定义，弹性模量E=210 GPa，泊松比ν=0.3。Y形密封圈材料为丁腈橡胶，使用Mooney-Rivlin两参数超弹性本构模型表征其非线性力学性能，其应变能密度函数[15]为

W=C10(I1-3)+C01(I2-3)+(J-1)2/d

(12)

式中：I1、I2为第一、第二应变不变量；C10、C01、d为材料常数；J为体积变化率。

d的计算式如式(13)所示，其中ν为材料的泊松比；取C01=0.202 MPa,C10=6.585 MPa[16],ν=0.495。

d=(1-2ν)/(C10+C01)

(13)

2.3 有限元模型

由于橡胶材料具有完全不可压缩或近似不可压缩性质，其泊松比接近0.5，对其进行有限元计算时可能出现由于单元刚度过大造成的体积锁定问题而导致计算发散，因此对Y形密封圈使用mixed u-P算法，以提高计算模型的收敛性。

接触设置如图4所示，模型中共设置三对非对称接触，接触单元和目标单元分别使用CONTA172和TARGE169单元，接触算法选择法向拉格朗日算法，以获得精确的接触计算结果。

图4 接触关系示意

为提高模型的收敛性，使用PLANE182单元对Y形密封圈划分四边形主导的面网格，并对Y形圈上A、B接触对的接触区域及介质侧受载区域进行局部网格加密；对于密封沟槽、活塞杆使用PLANE183单元划分映射网格。网格划分结果如图5所示。

图5 密封系统网格模型

分析中共设置4个载荷步，分别模拟安装工况、静密封、内行程、外行程中Y形密封系统的密封特性。其中，在第1个载荷步中施加空载荷，接触算法会将几何建模时形成的初始穿透量消除，以形成过盈配合状态；在第2个载荷步中通过迭代法将介质压力施加到靠近流体一侧且接触压力小于介质压力的节点上；第3、4载荷步分别使活塞杆水平向左、右移动，模拟内、外行程的运动状态。

如图6所示，通过迭代法[17]施加压力载荷时，首先选定Y形圈与介质接触一侧的部分节点组成节点组，在该节点组上施加介质压力进行求解，并将位于该节点组两侧的节点的接触压力与介质压力比较，若接触压力不大于介质压力，则将该节点加入节点组。重复上述操作，直到两侧节点的接触压力超过介质压力，说明已经得到了准确的载荷施加位置。

图6 介质压力作用节点组

3 Y形密封性能分析

3.1 静密封性能分析

Y形圈在不同介质压力作用下的变形云图如图7所示,其中实线代表Y形圈变形前的形状。

图7 不同压力作用下Y形密封总变形(mm)

从图7(a)中可以看出，安装工况下，Y形圈上半部分首先发生径向收缩，形成过盈配合。如图7(b)—(f)所示，介质压力作用后，Y形圈被轴向压缩，根部区域发生径向扩张，两侧分别向活塞杆外表面及密封沟槽内壁靠近；随着介质压力增大，接触对A、B的接触面积逐渐增大，Y形圈根部被挤入密封沟槽与活塞杆之间的密封间隙。

Y形圈根部靠近密封间隙区域在不同介质压力下的等效应力和Y方向变形量(即挤入长度)变化趋势如图8所示，其中趋势线下方为该区域的变形云图。

图8 Y形圈根部区域等效应力、Y方向变形量变化趋势

从图8可以看出，低压工况下，Y形圈根部不会被挤入密封间隙，根部等效应力随介质压力升高而快速增大；当介质压力超过12 MPa后，挤入长度和等效应力随介质压力近似线性增大；介质压力为18 MPa时，根部区域等效应力超过10 MPa。因此，对于在高压工况下使用的Y形密封，为防止其被挤入密封间隙而出现咬伤现象导致密封失效，应在密封圈根部增设倒角或增大Y形圈内径。

规定密封性能指数α(即主密封面最大接触压力与介质压力的比值)作为密封可靠性的评价指标。不同介质压力下，主密封面最大接触压力pcmax、密封性能指数α的变化趋势如图9所示，其中点线图下方为不同压力下的主密封面接触压力分布图。

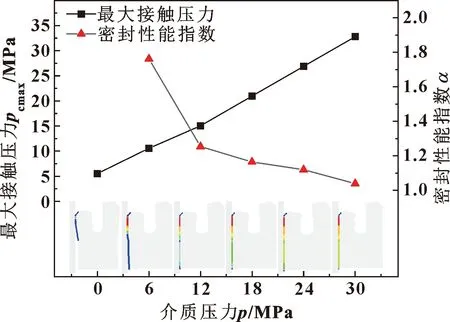
图9 主密封面最大接触压力、密封性能指数变化趋势

从图9可以看出，形成过盈配合后，主密封面最大接触压力仅有5.530 3 MPa，且有效接触区域很小，因此Y形密封抵抗压力冲击的能力较弱[18]；随着介质压力升高，主密封面最大接触压力近似线性增长，说明Y形密封在静密封状态下具有自紧密封特性。但是密封性能指数随介质压力升高而降低，说明密封的可靠性随之降低。当介质压力达到30 MPa时，密封性能指数降至1.093 1，最大接触压力接近介质压力。在实际工况下，为避免压力波动造成的静密封失效，应保证Y形圈工作压力小于30 MPa。

3.2 动密封性能分析

不同介质压力下，内、外行程中主密封面上的最大介质压力如图10所示。内、外行程最大接触压力均随介质压力增大而增大，且外行程最大接触压力大于内行程。当介质压力超过24 MPa时，内行程最大接触压力接近介质压力，这可能导致活塞杆密封在内、外行程转换及介质压力波动时出现宏观泄漏现象，因此在实际工作中，应使介质压力保持在24 MPa以下。

图10 不同介质压力下内、外行程主密封面最大接触压力

不同介质压力下，内、外行程接触压力分布如图11所示，其中横坐标为主密封面接触单元变形后的水平位置，左侧表示介质侧，右侧表示大气侧。该计算结果与文献[8]中的计算结果具有相近的分布规律，验证了数值模型的可靠性。介质压力超过6 MPa后，内、外行程接触压力分布趋势差别较大，但外行程中靠近介质一侧、内行程中靠近大气一侧均出现了压力梯度的拐点，通过对拐点附近压力进行拟合即可求出拐点处的压力梯度，代入式(8)、(10)可得ho、hi，进而得到不同压力下的泄漏量。

图11 不同介质压力下内、外行程主密封面接触压力分布

取介质动力黏度μ=0.035 Pa·s,活塞杆运动速度uo=250 mm/s,往复行程L=10 mm。不同介质压力下，活塞杆密封在外行程中的体积泄漏量、内行程中的体积泵回量如图12所示。

随着介质压力增大，体积泵回量呈线性下降趋势，体积泄漏量先减小后增大。往复过程中的净体积泵回量Q随着介质压力增大而减小，但始终为正值，这说明Y形密封在上述工况下的动密封性能较好。

4 Y形密封结构优化

根据Y形圈动、静密封状态下的性能分析可知，介质压力超过12 MPa后，Y形圈根部会被挤入密封间隙发生咬伤。为解决该问题，文中选用根部增设倒角的方法对Y形圈进行结构优化。同时，外行程中主密封面最大接触压力较大，这会提高Y形圈在运动过程中的磨损率[19]，降低Y形圈使用寿命；此外，虽然不同介质压力下活塞杆密封系统的净泵回量均为正值，但是由于活塞杆表面粗糙度的存在及压力波动等因素，仍会有部分液压油吸附在活塞杆表面而造成微观外泄，因此应尽量提高作为往复密封性能评价指标的净泵回量大小，以提高Y形密封的动密封能力，降低泄漏量。

为降低Y形圈的磨损率并减少其微观泄漏量，利用响应面优化方法，对倒角的形状参数H(与密封沟槽接触的直边段长度)、V(与活塞杆接触的直边段长度)进行最优化设计。以往复行程中的净泵回量作为目标函数，外行程中主密封面最大接触压力不大于16 MPa为约束条件建立响应面优化模型，所构建的响应面如图13所示。

图13 主密封面最大接触压力和体积响应面

响应面优化结果如表1所示，将响应面预测的最优解圆整后进行验证。优化后净泵回量提高8.66%，主密封面最大接触压力下降21.36%,Y形圈根部没有被挤入密封间隙;在提高Y形密封动密封性能的同时降低了磨损率，提高了密封系统的可靠性。

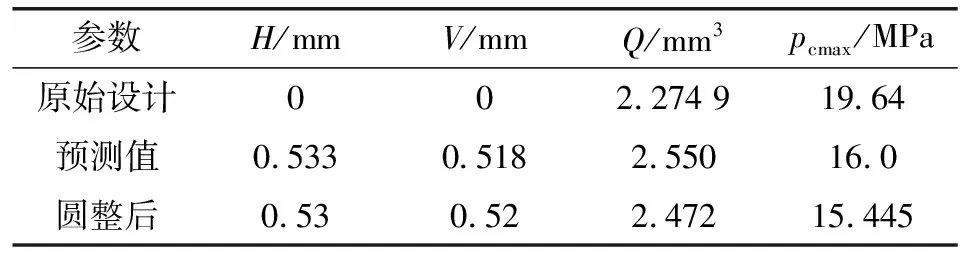
表1 优化前后密封性能

5 结论

(1)利用有限元方法及往复密封基本原理分析了不同工况下液压缸活塞杆用往复Y形密封的动、静密封性能，研究表明：Y形密封在安装工况下抵抗压力冲击的能力较弱；随着介质压力增大，Y形密封在静密封状态下的密封性能指数、动密封状态下的净泵回量均有所下降，防止泄漏的能力降低；高压工况下，Y形密封抗挤出能力降低，根部被挤入密封间隙，将出现咬伤现象导致密封系统失效。

(2)为提高Y形密封在高压工况下的往复密封性能，采用根部倒角的方法进行结构优化；针对以往Y形密封最优化设计中没有考虑的泵回量这一密封性能，使用Design Expert 建立响应面优化模型对倒角的几何参数进行最优化计算。优化后Y形密封的泵回量提高，磨损速度下降，咬伤现象消失，密封的可靠性提高。