基于灰色理论的尼龙/碳钢摩擦副磨损量预测*

管永强 王建梅 侯定邦

(太原科技大学重型机械教育部工程研究中心 山西太原 030024)

尼龙是一种种类多、用途广泛的工程塑料[1-2]。尼龙66常作为齿轮、轴 套、轴承保持架等基础传动连接件，实现转矩和轴向力的传递[3-4]。尼龙66制成的传动连接产品的失效一般包括疲劳失效和磨损失效，其中疲劳失效寿命可以根据材料的力学性能和应用工况进行优化设计，但是磨损失效缺乏完善的材料磨损量的指导，无法开展有效的“磨损量-使用寿命”的设计计算。

为有效提升尼龙产品设计应用水平，控制其机械制品的综合使用性能，通过优化尼龙材料的组成或添加特殊材料来提升其性能是一种常见的手段。陈保磊等[5]制备了浇铸(MC)尼龙、含油质量分数为5%的MC油尼龙、质量分数30% 的玻璃纤维增强MC尼龙及体积分数35%的碳纤维增强MC尼龙等4种尼龙复合材料，研究表明，干摩擦条件下摩擦因数由大到小依次为浇铸尼龙、玻璃纤维增强MC尼龙、碳纤维增强MC尼龙、MC油尼龙。蔡力锋等[6]通过熔融共混制备了热塑性聚氨酯/尼龙6(PA6)复合材料，发现制备的复合材料较PA6材料在高载荷下的耐磨性大幅度提高。张士华等[7]制备了玻璃纤维增强MC尼龙复合材料，并且定量研究玻璃纤维对尼龙材料摩擦磨损性能的影响，获得高耐磨性的玻璃纤维增强MC尼龙复合材料，并且针对尼龙材料的摩擦磨损机制进行了深入探究。李国禄等[8]针对玻璃纤维增强MC尼龙复合材料开展摩擦磨损试验，得出该复合材料的磨损机制主要表现为疲劳剥落和磨粒磨损。

虽然高性能材料能有效提升产品的使用性能，但是为高效地使用材料，需要在产品设计阶段充分认识材料的机械性能。在机械传动领域，尼龙66常被用来制作基础传动件，磨损是其主要的失效形式，所以在设计阶段考虑变载工况下磨损量对使用寿命的影响是必要的。磨损量的预测通常采用PLSR(偏最小二乘回归)[9]、BPNN(BP神经网络)[10]及灰色系统理论[11]等方法。

灰色系统理论是邓聚龙教授于1982年创立的，它从系统的角度出发结合数学方法来研究系统模型不准确、行为信息不完全、运行机制不清楚这类系统的建模、预测、决策(评价)和控制等问题[12-13]。国内外学者基于灰色预测法对相互运动的摩擦组件的磨损量进行预测，并取得可靠的效果。张晓南等[14]将灰色预测模型与BP网络相结合，建立了优化灰色神经网络预测模型，实例分析结果表明，优化模型能更精确地预测发动机气缸套的磨损量。LI等[15]基于磨损特征序列建立了代谢GM(1,1)灰色决策模型，预测了刀具磨损状态的变化趋势，从而为刀具更换提供依据。易怀军等[16]采用灰色模型对刀具的磨损进行预测，最终获得相对预测误差小于5%的预测模型。PRESTON[17]指出磨损深度的变化率与接触压力p和滑动速度v成正比。SUTTON等[18]根据磨损量的唯象定律，并考虑到部件几何形状的影响，从第一性原理推导出预测球和平面相互滑动时的磨损深度公式。LIN等[19]采用灰色理论建立刀具磨损量预测模型，并且采用磨损深度表征刀具的使用寿命，结果证明该灰色模型的相对预测误差小于5%。可见，以磨损深度为基准建立表面接触应力与磨损量的预测模型是可行的。

以尼龙66和45钢组成的摩擦副摩擦磨损试验，采样难度大、成本高、要求设备比较复杂；并且尼龙66相较于45钢的可塑性强、磨损状态不稳定，难以获得有效的磨损量预测模型，因此应采用包容性强的灰色理论进行磨损的预测[20-22]。

本文作者基于灰色理论，引入最小平衡系数，以磨损深度为基准建立了表面接触应力与磨损量的预测模型，并且通过磨损试验进行验证，证明了该预测模型的可靠性。表面接触应力-磨损量预测模型的建立，有效解决了不同工况作用下尼龙零部件磨损寿命的设计问题；该方法无需开展大量重复性的磨损试验，能够快速为尼龙零部件的产品设计提供磨损量的参数指标。

1 试验研究

采用WDW-200E型微机控制电子式万能试验机对试样进行单向拉伸试验，获得材料的载荷/位移关系，进而求出应力/应变曲线。试验试样采用尼龙材料制备，基于国家标准GB/T 1447—2005纤维增强塑料拉伸性能试验方法开展研究。文中试验制备3个标准试样(见图1)，试样试验区长度为50 mm，宽度为20 mm，厚度为5 mm。

图1 尼龙66的拉伸试样

拉伸试验试样的失效形式均为中部断裂，符合材料拉伸断裂标准特征，提取3组试验弹性变形到拉伸断裂阶段应力应变的数据并求取平均值作为尼龙66应力应变的标准取值。绘制尼龙66的应力/应变曲线,如图2所示，曲线规律符合材料拉伸断裂的基本趋势，证明拉伸试验结果可靠。通过曲线获得试验用尼龙66的屈服强度为94.651 MPa，拉伸强度为98.923 MPa。

图2 尼龙66的应力应变曲线

与尼龙66对磨的摩擦副采用45钢，45钢的硬度远远高于尼龙66，故45钢不发生磨损行为。查阅国家标准(GB 699—88)，获得45钢的屈服强度≥355 MPa，抗拉强度≥600 MPa。

采用MS-9000多功能腐蚀试验机(见图3)对尼龙66开展摩擦磨损试验，试验采用自动加载方式进行，上摩擦副采用45钢球，直径为6 mm，下摩擦副采用尼龙66，试样为长方体，规格为10 mm×5 mm×3 mm。试验加载过程中，下摩擦副保持静止，上摩擦副基于自动加载模块缓慢加载至试验值。加载完成后上摩擦副静止，下摩擦副进行往复运动。

图3 MS-9000多功能腐蚀试验机

在理想工况环境下，从设计角度分析，影响尼龙磨损量的关键因素是载荷。因此文中采用控制变量法，以载荷为自变量，控制温度、行程、运动形式不变，在5、10、15、20、25、30 N不同加载工况下进行干摩擦磨损试验，并采用Hertz接触理论计算各载荷作用下的表面接触应力。为了得到更为显著的试验结果，设置下摩擦副的运动频率为10 Hz，试验时间为30 min，试验温度为常温，摩擦形式为干摩擦，运动形式为往复运动。

2 试验结果及分析

摩擦磨损试验完成后，采用基恩士VHX-2000超景深显微镜对尼龙66试样的磨痕进行观测，获得磨痕的形貌及尺寸。如图4所示为6组载荷作用下尼龙66磨痕的显微形貌，发现各组试样磨痕均匀可靠。表1展示了5、10、15、20、25、30 N 6组载荷作用下的磨痕深度。为保障结果的可靠性，对每组载荷下3次试验的试样进行观测并求取平均值。

图4 不同载荷下尼龙66磨痕形貌

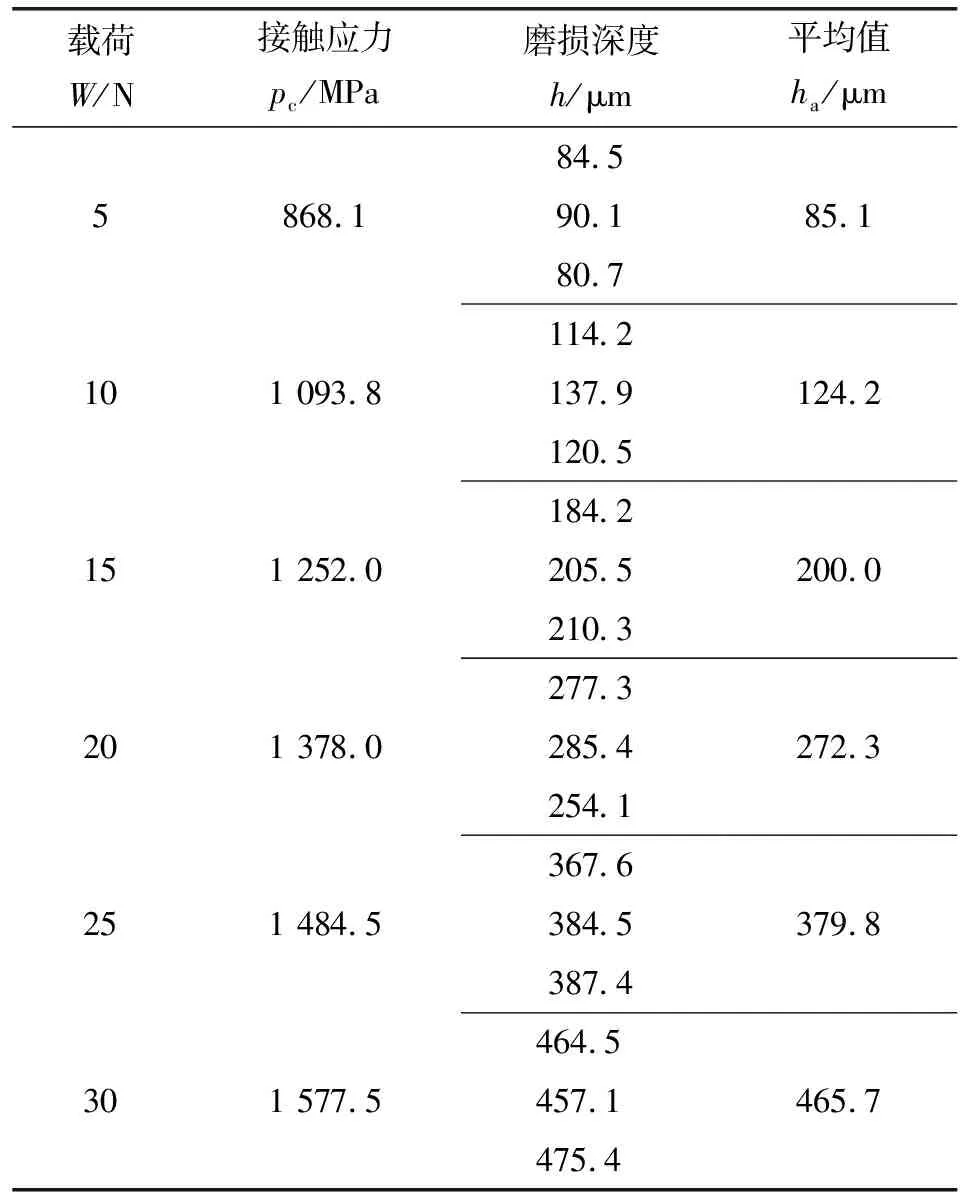
表1 各组摩擦磨损试验的磨痕深度

如图5所示为试验载荷、表面接触应力与磨损深度的关系曲线。可以看出，试验载荷和表面接触应力与磨损深度呈非线性正相关，所以无法直接采用线性函数获取磨损深度与载荷的函数关系。

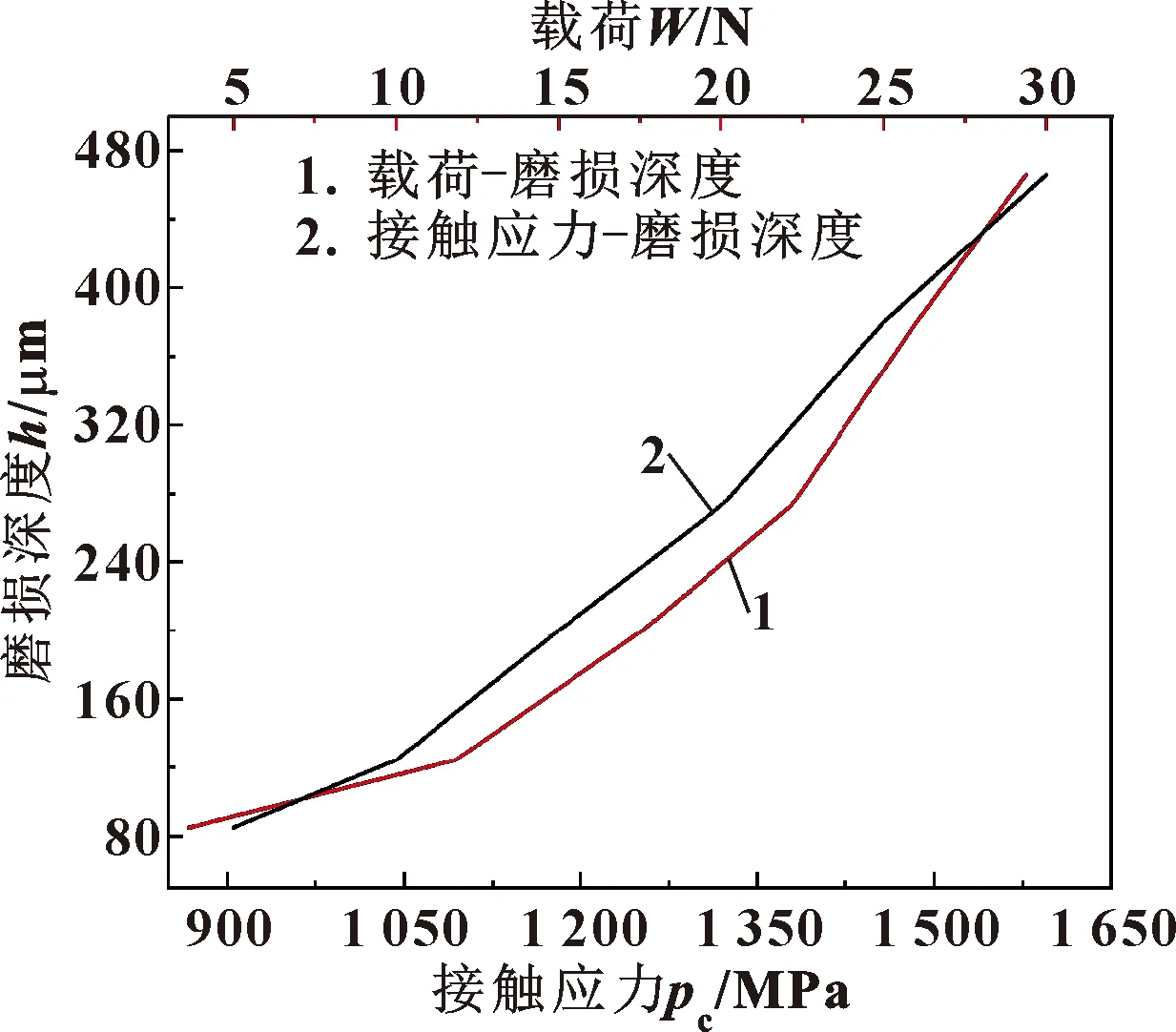
图5 磨损深度随载荷、表面接触应力的变化

3 灰色理论预测模型

为保障模型的可靠性，需要对数据做必要的检验处理，选取每组载荷下的磨损深度的平均值为原始数据，并记为

x(0)={x(0)(1),x(0)(2),…,x(0)(n)},n=1,2,…，6

(1)

将摩擦磨损试验测得的磨损深度代入式(1)，得到x(0)={85.1,124.2,200.0,272.3,379.8,465.7}，对原始数据进行级比检验，验证原始数据的可行性。级比计算公式如下：

(2)

采用式(2)计算得到原始试验数据的级比为：λ(0)={0.704,0.621,0.734,0.717,0.816}，级比的可容覆盖范围为λ=(0.751，1.284)。原始数据的级比不能全部落入可容范围，最低级比为0.621，无法有效建立灰色模型。所以引入平衡系数对数列x(0)进行变换处理，使其全部落入可容覆盖内。取常数c对数列x(0)进行平移变换：

y(0)(k)=x(0)(k)+c，k=1,2,…，n

(3)

使变换之后的数列y(0)(k)的级比都可以落入可容覆盖λ=(0.751，1.284)。通过式(3)不难发现数列y(0)(k)和x(0)(k)的级比呈一致性，所以只需找出数列x(0)(k)的最弱级比，并使数列y(0)(k)的相关数据满足可容覆盖范围即可，获得数列x(0)(k)的最弱级比为λ2=x(0)(2)/x(0)(3)=0.621，建立最低可容平衡方程，通过式(4)计算得到最小平衡系数c：

(4)

通过式(4)计算得到c≥118，考虑到对原始数据的保护，取平衡系数c=118，获得平移变换后的数列y(0)(k)为

y(0)(k)={203.1,242.2,318.0,390.3,497.8,583.7}

(5)

计算验证y(0)(k)数列均在可容覆盖范围。对原始数据进行积累，生成新的离散序列：

(6)

得到：x(1)={203.1,445.3,763.3,1 153.6,1 651.4,2 235.1}

建立灰微分方程：

(7)

计算得到微分方程的通解为

(8)

当t=1时，计算得到C：

(9)

将C代入通解：

(10)

使t=t+1，代入式(10)，得到：

(11)

将式(11)减去式(10)，得到：

(12)

已知y(0)(1)=x(1)(1)，可以得到：

(13)

采用线性回归求解a、b：

(14)

采用MatLab2016编程计算得到a=-0.211 8，b=184.792 9，代入式(13),得到：

e-0.211 8)

(15)

考虑最小平衡系数c，得到尼龙66与45钢摩擦副在不同载荷下的磨损量的灰色预测模型：

e-0.211 8)-c

(16)

通过式(16)的磨损量预测模型和表1的磨损深度试验值，绘制得到磨损深度的预测曲线和试验曲线如图6所示。可以发现试验值与预测值曲线重合度高，并且随着表面接触应力的增大，尼龙66的磨损深度曲线呈指数型增长，主要是因为45钢的硬度和强度远大于尼龙66，所以表面接触应力过大会直接导致尼龙66发生剧烈塑性变形，加剧磨损。

图6 灰色模型预测结果和试验结果比较

采用灰色预测模型分别计算5、10、15、20、25、30 N下的磨损深度，并分别计算各载荷作用下预测值与试验值的相对误差如表3所示。可见，载荷为10 N时的误差最大，相对误差为9.25%，载荷为20 N时的误差最小，相对误差为0.99%，平均相对误差为3.60%。

表3 灰色模型磨损深度预测值和误差

4 结论

(1)开展不同载荷作用下尼龙66与45钢配对的摩擦磨损试验，试验结果表明，磨损深度随表面接触应力呈指数型增长关系。

(2)采用灰色理论建立尼龙66与45钢摩擦副的磨损量预测模型，针对尼龙66与45钢配对试验的磨损深度不能完全适应灰色理论问题，引入平移变换概念，建立磨损量的最小平衡方程，获得在灰色理论可容覆盖范围的优化磨损深度。基于优化后的磨损深度，考虑表面接触应力与磨损深度的映射关系，建立了尼龙66磨损量的预测模型，该模型能够快速为尼龙零部件的产品设计提供磨损量的参数指标。

(3)建立的模型的预测值与试验值最大相对误差为9.26%，最小相对误差为0.99%，平均相对误差为3.60%，预测结果精度较高，预测模型可靠。