考虑粗糙度时不同衬层材料水润滑轴承润滑特性比较*
杜媛英 闵 为 刘晓艺 曹沁鑫 权 辉
(兰州理工大学能源与动力工程学院 甘肃兰州 730050)
水润滑轴承一般采用新型非金属材料作为衬层材料,赛龙、飞龙、丁腈橡胶(NBR)和超高分子量聚乙烯材料(UHMWPE)作为目前水润滑轴承中应用较广且备受关注的几种新型衬层材料,具有优异的物理学性能,相比于金属轴承而言,它们更容易形成弹流润滑水膜。然而,大多数的非金属材料,其弹性模量相对较低,在进行机械加工时一般很难达到与金属相同等级的表面粗糙度;同时,水润滑轴承在非稳定工况运行时,转子和轴承之间的间隙会变得极小,此时,其表面粗糙度对润滑特性的影响不能忽略。
国内外学者们对表面形貌和衬层材料等单一因素对水润滑轴承润滑特性的影响做了很多研究。例如在20世纪80年代,国外学者GOGLIA等[1]、ZHU和CHENG[2]分析了表面形貌对弹流润滑特性的影响。近年来,也有很多学者探讨分析了表面粗糙度对水润滑轴承润滑特性的影响。NADUVINAMANI等[3-4]研究了表面粗糙度对阶梯滑动轴承弹流润滑特性的影响,发现负偏斜的表面粗糙度增大了摩擦因数。王优强等[5]考虑固体颗粒和粗糙度的影响,分析了水润滑飞龙轴承热弹流润滑性能,发现粗糙度和固体颗粒的尺寸对飞龙轴承的润滑水膜厚度及水膜压力影响很大。LIN等[6]基于Eringen的微连续谱理论和Christensen的随机理论,研究了非牛顿流变学和表面粗糙度对滑动轴承动态特性的综合影响,结果表明,与用微极性流体润滑的光滑轴承相比,横向粗糙度的影响增大了承载能力和动态系数,而纵向粗糙度的影响正好相反。王家序等[7]利用摩擦试验机分析了载荷、速度、运行时间等因素对水润滑塑料轴承摩擦因数和磨损率的影响。WANG等[8]分析了UHMWPE、聚四氟乙烯以及其他复合材料在海水中的摩擦学特性。最近,杜媛英和李明[9-11]分析了考虑轴颈倾斜和表面粗糙度的水润滑橡胶轴承的润滑特性,发现轴颈倾角和表面粗糙度会使得水膜厚度和水膜压力呈锯齿状分布,同时采用数值模拟方法对不同衬层材料下的水润滑轴承特性进行了研究。崔旨桃等[12]探讨了尼龙自润滑性与表面织构协同作用对水润滑轴承摩擦磨损性能的影响。王亚兵等[13]针对船舶艉轴承轴颈受载倾斜产生的摩擦磨损问题进行了详细分析。
综上,目前对水润滑轴承的研究大多基于单一因素影响下其润滑特性的分析。为此,本文作者以水润滑轴承为研究对象,考虑表面粗糙度的影响,针对备受关注的几种新型非金属衬层材料,建立润滑数学模型,研究考虑实际表面粗糙度时,几种新型衬层材料的衬层变形、水膜厚度和水膜压力的变化规律。研究结果具有重要的工程实际意义。
1 水润滑橡胶轴承结构及基本参数
1.1 水润滑橡胶轴承结构及参数
水润滑橡胶轴承结构及坐标系如图1所示。其中转子绕轴颈中心Om转动,ns为转速,轴承中心为O,e为偏心距,φ为偏位角,h为水膜间隙,轴承半径为R0,轴颈半径为R,x为轴颈的旋转方向。轴颈旋转时,流体动压润滑在水润滑橡胶轴承的间隙中形成。水润滑橡胶轴承结构参数如表1所示。
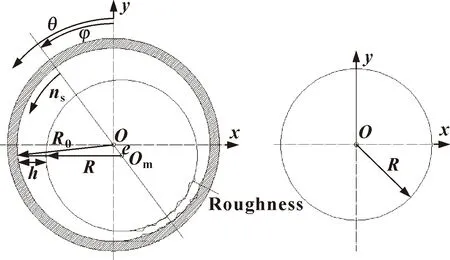
图1 全圆周水润滑轴承示意

表1 水润滑橡胶轴承结构参数
1.2 衬层材料及基本参数
选取性能优越且目前备受关注的4种新型衬层材料作为研究对象,分别是飞龙、赛龙、UHMWPE和NBR。4种衬层材料的基本参数如表2所示。
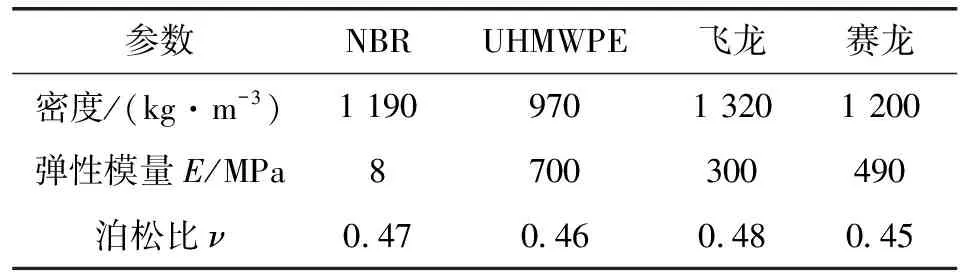
表2 不同衬层材料基本参数
2 表面粗糙度的测量
以某水润滑橡胶轴承为测量对象,如图2所示,利用TIME3230表面粗糙度测量仪对轴承表面粗糙度进行测量,得到橡胶轴承实际表面粗糙度分布的波幅和波长的原始数据,并进行去噪处理,发现去噪后的粗糙度分布由一系列的正弦波和余弦波组成。因此,为了数值计算方便,采用余弦函数来表征轴承表面粗糙度的分布。
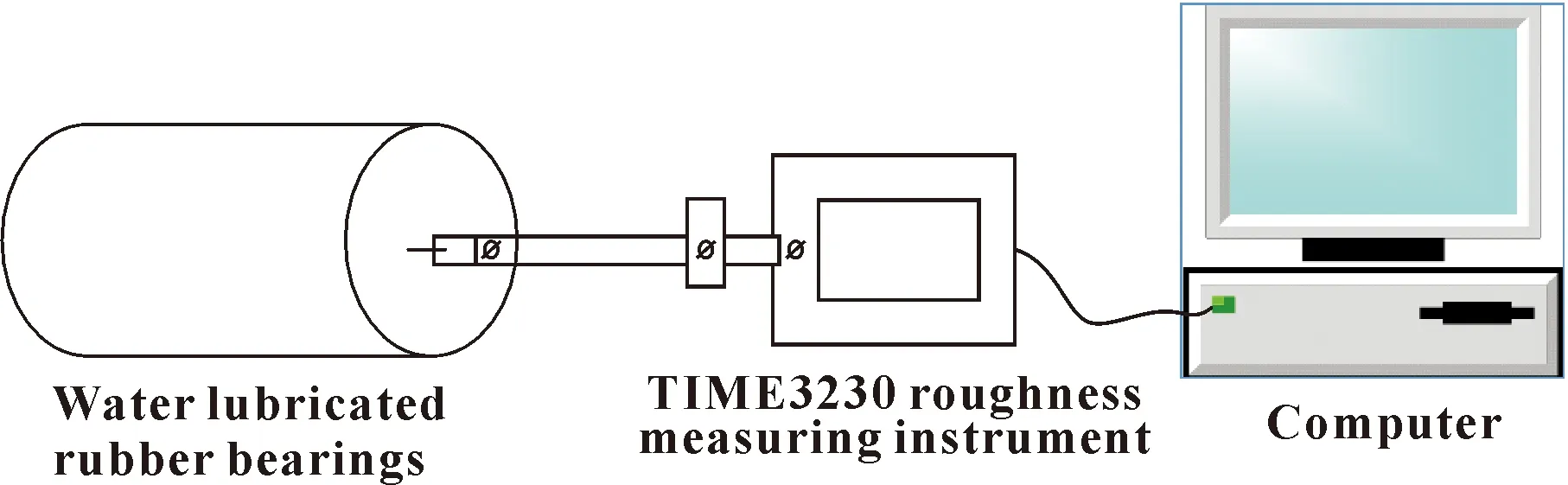
图2 水润滑橡胶轴承表面粗糙度的测量
由于粗糙度为纵向纹理,则其表面分布可以表示为
s=Acos(2πx/ls)
(1)
式中:A为表面粗糙度的幅值;ls为粗糙度的波长。
3 控制方程
3.1 润滑方程
水润滑橡胶轴承在实际运行时,由于橡胶衬层变形较大,水的黏度较低,其实际润滑水膜内多为层、湍流共存的混合流态,实际雷诺数不再是某一定值,而是随它的实际水膜厚度变化而变化的。因此采用混合流润滑条件下的润滑方程。
混合流润滑理论下水润滑橡胶轴承的润滑方程[9]为
(2)
式中:x、z为圆柱坐标系的2个坐标轴;p为润滑膜压力;μ为润滑剂动力黏度;ω为轴颈角速度;由于青木弘-原田正躬湍流润滑理论在水润滑轴承的实际应用中更具优越性,因此文中采用其作为湍流润滑时的润滑方程[14],其中kx、kz为湍流因子,kx=1+(0.013 92/12)Re0.916;kz=1+(0.014 4/12)Re0.854。
水膜压力的量纲一化形式可表示为
(3)
式中:θ为水润滑橡胶轴承的量纲一周向坐标;λ为量纲一轴向坐标;H为量纲一水膜厚度;P为量纲一水膜压力;L为轴承长度;d为轴颈直径。
量纲一化所用的特征量为
(4)
式中:c为轴承间隙。
3.2 水膜厚度
3.2.1 弹性变形
水润滑橡胶轴承衬层的弹性变形[15]为
(5)
式中:Δh为衬层变形量;p(ζ)为水膜压力;x-ζ为压力作用点与弹性变形计算点之间的距离。
3.2.2 水膜厚度方程
考虑粗糙度的水润滑轴承的水膜厚度包括轴承与转子间的间隙、非金属衬层材料的变形量及粗糙度。将表面粗糙度函数式(1)代入水膜厚度方程,可得到水润滑橡胶轴承量纲一化之后的方程为
H=1+εzcos(θ-φz)+ΔH-S
(6)
式中:ε为轴承的偏心率;θ为周向角度;φ为偏位角;ΔH为量纲一弹性变形量;S为量纲一化的粗糙度函数。
3.3 平衡方程
水膜压力与载荷达到平衡时,水膜压力在x轴和y轴上的分力为Wx和Wy,水膜承载力W为
(7)
4 数值计算方法及有效性分析
4.1 数值计算方法
采用有限差分法离散方程(2),将求解域沿轴向λ和周向θ划分为n和m个等距区间,求解域定义为0≤θ≤2π,-1≤λ≤1,计算网格的控制域为 120×120个等距的节点。利用半步长中心差分格式可求得水膜压力。图3所示为求解域的网格划分和差分格式示意图。
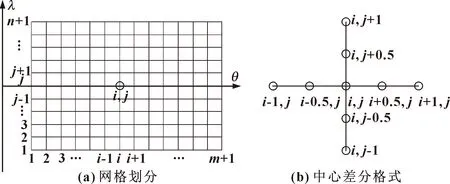
图3 网格划分和中心差分格式示意
边界条件为自然破裂,由式(3)可求得各节点的Pi,j。通过MATLAB编写相关分析程序,利用超松弛迭代方法提高计算的精度和效率,收敛精度均为0.000 01。
4.2 润滑模型的实验验证
采用与文献[16]水润滑橡胶轴承试验相同的几何和工况参数,将文中计算结果与文献[16]的试验结果进行比较分析,进行程序的有效性验证。图4所示为文中润滑模型计算的水膜压力与文献[16]试验获得的水膜压力沿轴向的变化曲线。
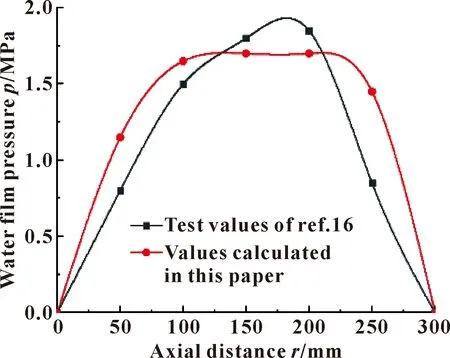
图4 文中模型计算的水膜压力与文献[16]试验获得的水膜压力比较
由图4可以看出,文中计算得到的平均水膜压力与试验获得的最大水膜压力误差在6%以内,沿轴向大约80%的区域为橡胶轴承的主要承压区。这证明文中模型可以有效进行水润滑轴承润滑特性的分析。
5 数值计算结果及分析
采用试验获得的实际表面粗糙度的幅值和波长,分析4种不同衬层材料下水润滑轴承的衬层变形、水膜厚度和水膜压力沿轴承周向和轴向的变化特点,探讨了不同转速下几种衬层材料的承载力和最大水膜压力变化规律;同时也比较分析了考虑粗糙度与表面光滑水润滑轴承的润滑特性。
5.1 衬层变形的变化规律
考虑表面粗糙度时,对NBR、飞龙、赛龙及UHMWPE材料水润滑轴承在转速ns=300 r/min、偏心率ε=0.6工况下的变形分布进行数值计算,并与表面光滑的NBR衬层材料进行对比,结果如图5所示。
由图5(a)(b)可以看出,考虑表面粗糙度的4种衬层材料沿轴向的衬层变形分布均呈“簸箕形”,在进出口变形速率较快,在中部变形最大。分析图5(a)可知,考虑表面粗糙度时NBR材料的轴向水膜厚度略小于表面光滑的NBR材料,同时受到粗糙度的影响,考虑表面粗糙度的NBR材料的水膜厚度呈连续的小波状分布。综合分析图 5(a)(b)可知,光滑NBR材料的衬层变形最大,最大变形量约为5×10-4,飞龙、赛龙和UHMWPE材料的衬层变形均在5×10-7~1.3×10-5之间;4种衬层材料变形量由大到小依次是NBR、赛龙、飞龙、UHMWPE。由图5(c)(d)可以看出,考虑表面粗糙度的4种衬层材料沿周向的变形呈“正弦波状”分布,且在周向角度为140°时达到最大,表面粗糙度使得衬层变形呈波状分布。分析图5(c)可以发现,表面粗糙度对最大衬层变形的影响不大。综合分析图5(c)(d)可知,NBR衬层材料的变形最大,最大变形约为1.3×10-3,飞龙、赛龙和UHMWPE材料的变形均在3.5×10-8~5×10-7之间;4种材料的变形量由大到小依次是NBR、赛龙、飞龙、UHMWPE。
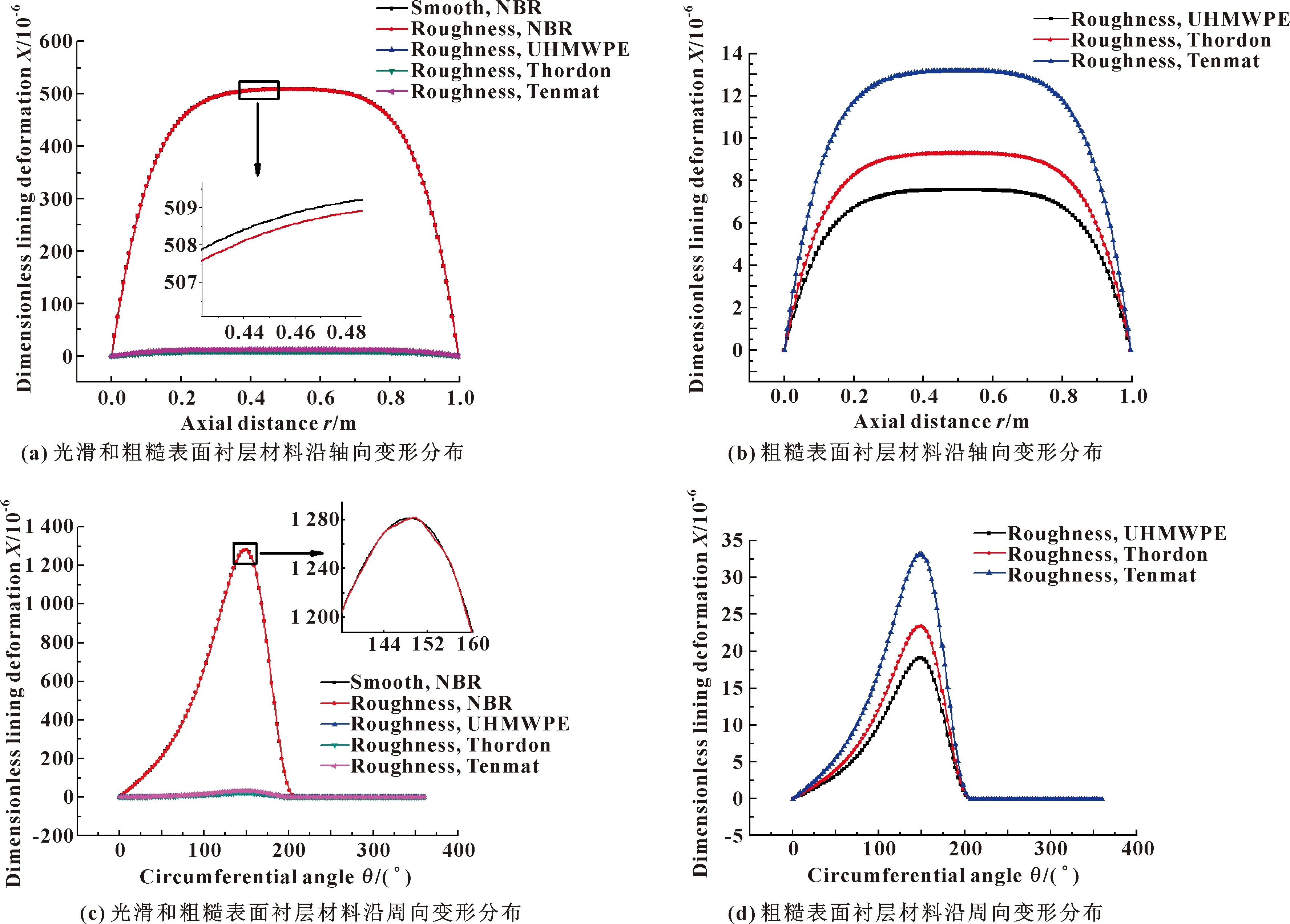
图5 不同衬层材料沿轴向和周向变形分布
5.2 水膜厚度分布
图6所示为光滑表面NBR和粗糙表面的NBR、飞龙、赛龙和UHMWPE 4种衬层材料沿轴向和周向的水膜厚度变化曲线。
由图6(a)(b)可以看出,粗糙表面的NBR衬层材料的水膜厚度明显小于光滑表面的NBR材料;4种衬层材料的轴向水膜厚度分布沿轴向均呈“簸箕形”,且在进出口变化速率快,在中部水膜厚度较厚,这说明在水润滑轴承内可以形成完整的润滑水膜。综合分析图6(a)(b)可知,表面光滑NBR衬层材料的水膜厚度最大,飞龙、赛龙和UHMWPE材料的水膜厚度在同一数量级,4种衬层材料沿轴向的最小水膜厚度由大到小依次是NBR、赛龙、飞龙、UHMWPE。由图6(c)可看出,4种衬层材料的变形沿周向均呈“正弦波”状分布,考虑衬层材料粗糙度时使得水膜厚度呈“锯齿状”分布。分析图6(c)可知,粗糙表面的NBR衬层材料的最小水膜厚度明显小于光滑表面的衬层材料,这说明粗糙度对最小水膜厚度有很明显的影响,它使得最小水膜厚度明显减小。4种衬层材料沿周向的最小水膜厚度总体相差不大,其中赛龙、飞龙和UHMWPE材料的水膜厚度在同一数量级,NBR材料的最小水膜厚度比其他3种衬层材料略大,这说明在相同的工况下,NBR衬层材料比其他几种衬层材料能更好地保持润滑水膜的完整性。

图6 不同衬层材料沿轴向和周向水膜厚度分布
5.3 水膜压力分布
对考虑表面粗糙度的4种不同衬层材料水润滑轴承的水膜压力进行了数值计算,并与光滑表面NBR衬层材料的水膜压力进行了对比分析。图7所示为表面粗糙度幅值A为4 μm、粗糙度波长ls为100 μm、转速ns为300 r/min、偏心率ε为0.6时,考虑表面粗糙度的NBR、飞龙、赛龙和UHMWPE材料以及光滑表面NBR材料沿轴向和周向的水膜压力变化曲线。
由图7可以看出,不同衬层材料的水膜压力沿轴向均呈现开口“簸箕形”,沿周向呈现类似“正弦波”状分布。分析图7(a)可知,NBR衬层材料的水膜压力比其他3种衬层材料小,同时粗糙表面的NBR材料的水膜压力小于光滑表面NBR衬层材料的水膜压力。UHMWPE、飞龙和赛龙材料的水膜压力基本处在同一数量级,且4种衬层材料水膜压力由大到小依次是UHMWPE、飞龙、赛龙、NBR。分析图7(b)可知,粗糙度使得几种衬层材料的水膜压力呈不规律的波状分布,而粗糙表面NBR衬层材料的水膜压力略小于光滑表面NBR衬层材料值。
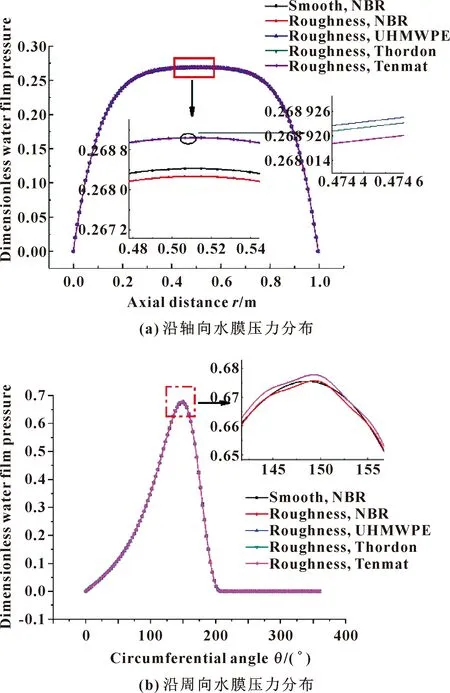
图7 不同衬层材料沿轴向和周向水膜压力分布
5.4 承载力和最大水膜压力随转速的变化
承载力和最大水膜压力是水润滑轴承性能优劣的重要指标。图8所示为偏心率ε=0.6时,不同转速ns下光滑表面NBR材料和考虑表面粗糙度的NBR、飞龙、赛龙及UHMWPE材料的承载力变化曲线。
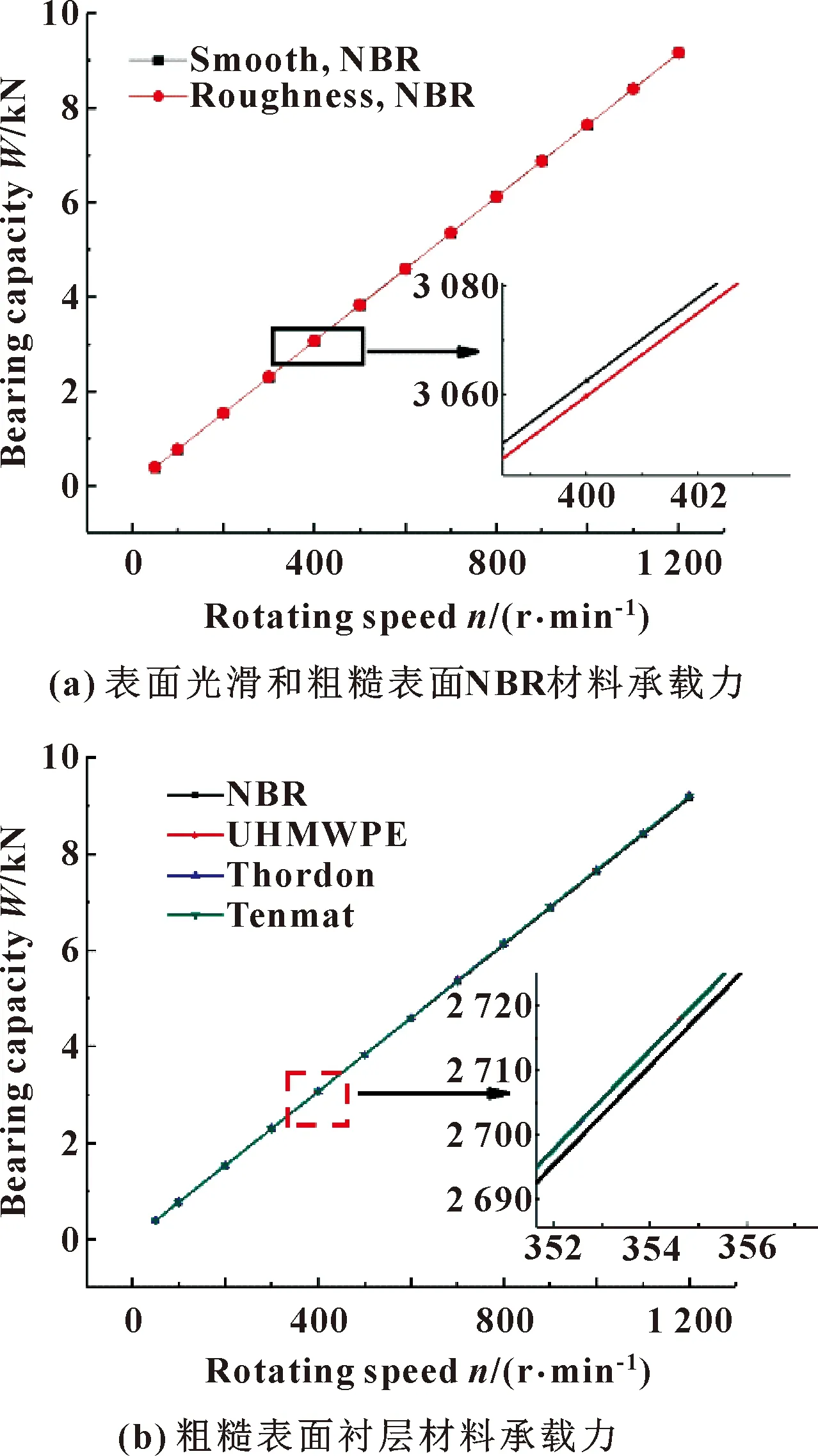
图8 不同衬层材料承载力随转速变化
由图8可看出,几种衬层材料水润滑轴承的承载力随转速ns的增大呈线性增大的趋势;NBR衬层材料的承载力最小,且光滑表面NBR衬层材料比粗糙表面NBR的承载力略大;飞龙、赛龙及UHMWPE材料的承载力大小在同一数量级。
图9所示为偏心率ε=0.6,不同转速下光滑表面NBR和考虑粗糙度的NBR、飞龙、赛龙及UHMWPE材料的最大水膜压力变化曲线。
由图9(a)可见,NBR衬层材料的最大膜压随转速ns的增大近似呈线性下降;光滑表面NBR衬层材料的最大水膜压力小于粗糙表面的NBR衬层材料。这是由于表面粗糙度会使得水润滑轴承的水膜压力出现一些局部的微小压力峰值。分析图9(b)可知,飞龙、赛龙及UHMWPE材料的最大水膜压力随着转速的增大变化较小,且处在同一数量级;而NBR材料的最大水膜压力随转速ns的增大呈近似线性减小,这是由于橡胶材料本身是高弹性体决定的。
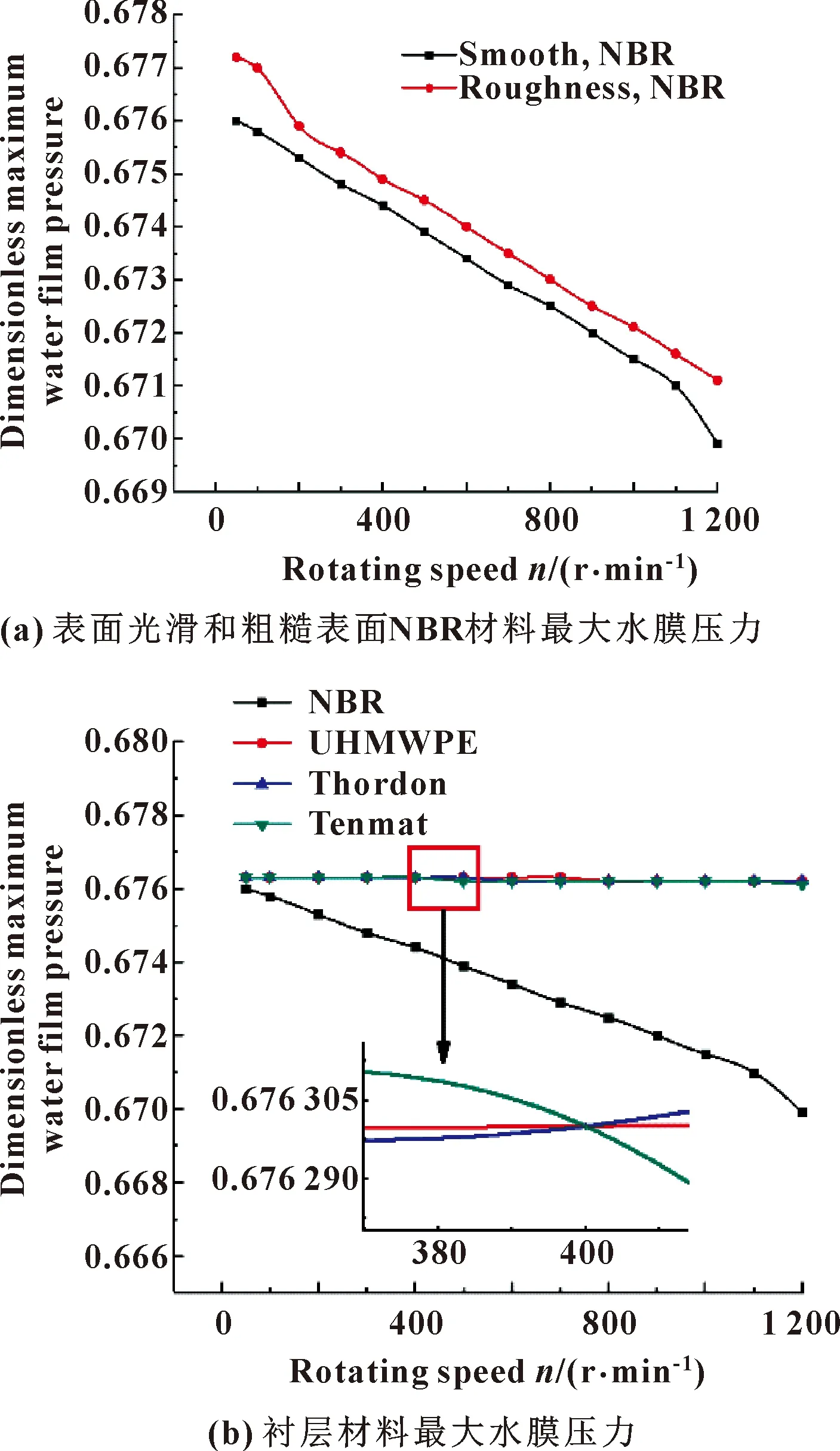
图9 不同衬层材料最大水膜压力随转速变化
6 结论
建立考虑粗糙度幅值和波长的几种不同衬层材料的水润滑轴承的润滑模型,利用混合流润滑模型研究表面粗糙度和不同衬层材料共同作用下水润滑轴承的润滑特性,并与表面光滑的衬层材料的水润滑轴承进行对比分析。主要结论如下:
(1)表面粗糙度使得水润滑轴承的衬层变形呈轻微波状分布,衬层变形减小;水膜厚度呈“锯齿状”分布,最小水膜厚度变薄;水膜压力有轻微的局部压力突变,最大水膜压力增大,承载力下降。因此,在进行轴承设计加工时,粗糙度的影响不可忽略。
(2)在相同工况下,NBR衬层材料相比飞龙、赛龙及UHMWPE衬层材料更容易形成润滑水膜,而UHMWPE衬层材料可以保证系统承受较大的承载力。
(3)4种衬层材料水润滑轴承的最小水膜厚度由大到小依次是丁腈橡胶、赛龙、飞龙、超高分子量聚乙烯,最大水膜压力由大到小依次是超高分子聚乙烯、飞龙、赛龙、丁腈橡胶;超高分子量聚乙烯、飞龙和赛龙衬层材料水润滑轴承的承载力在同一数量级,且明显大于丁腈橡胶衬层材料水润滑轴承的承载力;丁腈橡胶材料的最大水膜压力随转速的增加而减小。
上述研究对水润滑轴承的材料选型、结构设计、加工、装配有一定的参考意义,也可为后续分析水润滑橡胶轴承的动力学特性提供理论依据。

