钻井泵活塞缸套密封系统密封性能流-固耦合分析*

侯勇俊 都 磊 张芳芳 蒲宗珉 席建秋

(1.西南石油大学机电工程学院 四川成都 610500；2.宏华集团 四川成都 610036；3.宝鸡石油机械有限公司成都装备制造公司 四川成都 610052)

我国对石油天然气的开采随钻井工艺技术的进步而逐渐向深地层发展。随着钻井深度增加，地层情况越来越复杂，对钻井泵的工作压力要求也越来越高。在钻井泵液力端中，活塞缸套密封性能将直接影响到整个钻井生产的效率[1]。由于高压作业时，活塞的使用寿命和密封性能均急速下降，所以研究活塞的力学特性，不仅能分析出活塞失效的原因，还能为活塞后期的优化设计提供相应的指导依据。近年来，国内很多学者对活塞的使用性能进行了深入研究。王晓伟等[2]分析了活塞缸套的失效形式，并提出了合理使用缸套、活塞的方法。王新怡[3]通过有限元软件对活塞皮碗及连杆进行了力学分析，并针对其薄弱环节提出了改进措施。文献[4-6]通过观察生活中动植物形态，设计了多种仿生形活塞，并通过有限元软件ANSYS建立了仿生活塞三维轴对称结构，研究了仿生活塞受力特性。苑惠娟等[7]通过实验分析，对活塞的失效原因进行了归纳总结，并提出了提高活塞寿命的建议。

现有的相关研究大多都忽略了钻井泵工作过程中活塞缸套与钻井液的流-固耦合作用，得出的结论与实际的受力特性有一定的差别。本文作者以某2000HP型钻井泵活塞为研究对象，活塞缸套示意图如图1所示，基于Workbench下FSI流-固耦合分析模块，研究活塞在吸排液过程中不同工作压力下活塞缸套与钻井液流-固耦合作用的力学特征，同时探究过盈量和皮碗唇角等参数对活塞缸套密封性能的影响。

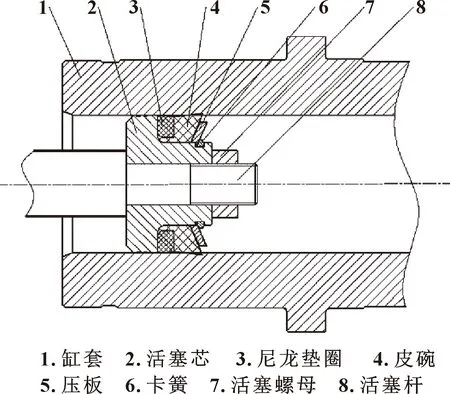
图1 2000HP型活塞缸套示意

1 数学模型

1.1 丁腈橡胶本构方程

活塞皮碗材料为丁腈橡胶，是一种高度非线性、不可压缩的超弹性体，一般的弹塑性理论不能准确地描述其力学特性[8]。当前针对橡胶材料的模型多样，文中选用Mooey-Rivlin模型来描述橡胶的力学特性[9-11]。超弹性本构模型通过应变能密度函数来定义，关系如下：

(1)

式中：W为应变能密度；Cij为材料常数；I1、I2、I3为变形张量；D为材料不可压缩参数，J为弹性体积比。

通过主伸长比λ1、λ2、λ3可得到I1、I2、I3，具体如下：

(2)

在橡胶材料单轴拉伸实验过程中，主伸长比λ1、λ2、λ3的关系如下：

(3)

式中：λμ为沿载荷方向上的主拉伸比；λ2、λ3为垂直于载荷方向上的主伸长比。

文中皮碗橡胶材料的本构模型采用两参数Mooey-Rivlin模型，则有：

W=C10(I1-3)+C01(I2-3)

(4)

式中的C10、C01通过橡胶材料的拉伸实验数据及ANSYS仿真软件拟合得到，最终得到C10=2.688 MPa，C01=4.021 MPa。

1.2 流-固耦合有限元理论

流-固耦合除遵循最基本的守恒原则，满足流体控制方程(质量、动量守恒方程)和结构域控制方程，还需在流固耦合交界面处，应满足流体和固体应力(τ)、位移(d)、热流量(q)、温度(T)等变量相等或守恒。但文中未考虑温度对活塞缸套的影响，因此在未考虑能量传递情况下的流-固耦合在交界处的控制方程应满足以下条件[12-13]：

(5)

式中：d为耦合边界位移；τ为应力边界(下标f、s分别代表流体和固体)。

2 模型及设置

2.1 几何模型及参数

根据2000HP型钻井泵活塞缸套尺寸，在三维建模软件中建立活塞缸套的几何模型，其中皮碗唇角θ=20°，过盈量λ=1.5 mm，缸套内径为114 mm。由于在钻井液的压力作用下，活塞缸套密封系统中卡簧和压板只是起到传递载荷的作用，对密封性能的影响较小，为避免模型过于复杂导致结果不收敛，将结构中非关键部位进行简化，其最终模型结构如图2所示。

图2 几何模型

皮碗材料为丁腈橡胶，垫圈材料为MC尼龙，其余结构材料采用结构钢，具体材料参数如表1。

表1 材料参数

2.2 网格划分及无关性分析

根据建立的活塞缸套模型提取的流体域模型采用四面体网格划分，并合理地分布网格的疏密，如图3(a)所示；固体域模型网格划分采用以四面体网格为主的方式，并对皮碗、垫圈、缸套内表面等重要的部位进行网格细化，如图3(b)所示。

图3 几何模型网格

为保证仿真结果的准确性和稳定性，需验证仿真模型的网格无关性。采用相同的物理参数和边界条件对整个耦合区域进行网格无关性验证，选取5组不同网格，计算得到皮碗在最大钻井液压力51.7 MPa作用下皮碗最大变形量，如表2所示。根据表2，最终选择网格节点为29 518，其中皮碗网格为2 574，此时最大变形量变化较小，满足计算精度和时间成本要求。

表2 网格无关性验证

2.3 边界条件

由于分析的是活塞在排吸液过程中，钻井液压力变化过程中不同压力下的活塞缸套的力学特征，而缸套内钻井液压力变化过程中，在不同压力值的各个瞬时状态下，活塞在缸套中都是处于平衡状态,故采用单向流-固耦合方法，流体计算采用稳态分析，结构计算采用静力学分析。

稳态流体分析：选定钻井液作为流体域材料，活塞排液过程中无入口边界条件，出口选用压力出口，由参考文献[14]通过理论计算和实验测试得到钻井泵缸套内压力变化规律，如图4所示。根据图4分别选取工作压力为0、10、20、30、40和51.7 MPa进行计算；选用k-ω湍流模型[15-16]；采用分离式求解器，压力速度耦合方式选用simple算法，采用二阶迎风格式进行求解；通过设置计算残差等参数来判断计算是否收敛。初始化后，迭代次数设置为2 000次，计算时间为1 s；计算完成后，将钻井液产生载荷导入固体域作为活塞受到的外载。

图4 缸套内压力变化曲线

稳态静力学分析：为得到正确的活塞缸套受力情况，文中根据钻井泵活塞缸套实际运行状态来设置接触和约束。由于皮碗和垫圈在钻井液压力作用下会沿轴向发生移动变形，所以将皮碗和缸套接触面、垫圈和缸套接触面都设置为摩擦接触(Frictional)，摩擦因数为0.124[17]；由于讨论的是活塞某一时刻静态受力特性，所以钢芯与缸套之间设置为固定约束(Fix Support)；活塞皮碗和钢芯接触面、垫圈和钢芯接触面之间没有间隙，同时又允许相互滑动，所以将其接触类型设置为不分离接触(No Separate)；活塞皮碗与垫圈是整体硫化黏结而成，皮碗与垫圈之间的接触面之间不允许相互滑动，所以将其接触类型设置为绑定接触(Bonded)。定义缸套固定不动，设置皮碗端面和缸套内表面为流-固耦合面。

3 结果分析与讨论

3.1 一个周期内皮碗受力变化趋势

根据缸套内压力变化规律，分别选取缸套内压力节点0、10、20、30、40和51.7 MPa为耦合计算压力，再根据凸轮转角所对应的缸套内压力绘制一个周期内各压力下皮碗与缸套接触面之间的最大等效应力、接触压力和摩擦应力曲线。

图5所示是皮碗与缸套接触面之间的最大等效应力、接触压力和摩擦应力随凸轮转角的变化曲线。可以看出，其变化规律同缸套内压力变化曲线相似，在凸轮转角0°～22°范围内，也就是排液阶段，皮碗与缸套间的最大等效应力、接触压力以及摩擦应力都随缸套内压力增大而增大；在凸轮转角为22°时，压力达到最大51.7 MPa，最大等效应力、接触压力和摩擦应力也达到最大；在凸轮转角为180°～202°时，此时进入吸液阶段，皮碗受力也随缸套内压力减小而减小；在凸轮转角为202°时，缸套内压力减小为0后，皮碗与缸套间的受力也减小到最小。

图5 一个周期内皮碗最大受力曲线

3.2 最大钻井液压力下活塞缸套受力情况

通过分析发现工作压力越大皮碗受力也越大，因此研究活塞缸套的密封性能时，需重点分析活塞缸套在51.7 MPa最大钻井液作用下的受力情况。通过计算得到在51.7 MPa钻井液作用下，缸套与活塞接触内表面、垫圈表面、活塞皮碗与缸套接触面的等效应力、接触压力和摩擦应力等。

缸套与活塞接触内表面等效应力分布如图6所示。可以看出，缸套内表面等效应力分布分为3个区域，活塞左端既没有与活塞接触，也不受钻井液压力作用，等效应力较小，为40～45 MPa；缸套与活塞接触处即为等效应力最大的区域，其变化规律与活塞皮碗尺寸的变化规律相同，由皮碗根部接触处至唇部逐渐增大，为60～109 MPa，在皮碗的唇部接触处等效应力最大；在活塞右端，仅有钻井液压力作用，等效应力分布较均匀，为55～60 MPa。总体来看，缸套内表面最大等效应力小于结构钢的屈服应力，表明缸套在51.7 MPa钻井液作用下，不会产生明显的变形，能够正常工作。

图6 缸套内表面等效应力分布

图7所示为垫圈表面等效应力分布。可以看出，由于皮碗属于非线性材料，所以垫圈的等效应力为非均匀分布。垫圈的等效应力主要集中在与皮碗接触的内圈表面，这是由于通过皮碗传递的钻井液压力首先作用在垫圈与皮碗接触的表面，同时皮碗受压会使其径向体积增加，导致与皮碗接触的垫圈内圈受到的等效应力大于外圈，为100～138 MPa。但由于垫圈材料为MC尼龙，综合性能良好，垫圈也不易失效。

图7 垫圈表面等效应力分布

活塞皮碗，相较于缸套和垫圈是活塞密封中最易失效的部位，也是文中研究的重点对象。皮碗上等效应力大小反映了皮碗表面各主应力的差值。当等效应力增大时，会加剧皮碗橡胶材料的松弛程度，降低其刚度，因而皮碗容易产生裂纹。由于橡胶材料的松弛程度和裂纹对活塞的密封性能有很大的影响，所以等效应力可间接反映活塞的密封性能[19]。图8(a)所示为活塞皮碗与缸套接触面的等效应力云图，图8(b)所示为皮碗沿轴向取一定间隔点绘制的等效应力曲线。可以看出，由于活塞皮碗是非线性材料，其等效应力是非均匀分布的。在皮碗的唇部和根部与垫圈接触的位置等效应力值较大，且唇部等效应力大于根部，为9～12 MPa。这是由于活塞在唇口处为过盈配合，在压力作用下橡胶产生形变使活塞达到密封效果；由于活塞皮碗直径从根部逐渐向唇部增大，其背部等效应力也由根部到唇部逐渐增大，为1～9 MPa；同时皮碗根部会出现挤入垫圈与缸套之间的趋势，所以皮碗根部与垫圈接触位置应力较大，为6～8 MPa。

图8 皮碗等效应力分布

活塞缸套密封为接触型密封，靠外部压力作用紧贴在密封面上，密封介质压力小于弹性体对表面的接触压力时就能形成良好的密封，所以接触压力的大小一定程度上能反映其密封性能。图9所示为活塞皮碗与缸套接触面间接触压力云图和曲线图。可以看出，2000HP型往复泵活塞皮碗接触压力从皮碗根部至唇部逐渐增大，这正与皮碗尺寸的变化规律相吻合。活塞皮碗表面接触压力也是非均匀分布的，皮碗唇部过盈量最大，所以此处的接触压力也最大，为60～72 MPa，且大于钻井液压力值。该仿真结果表明活塞在钻井液工作压力作用下密封性良好；皮碗背部接触压力值变化较为平缓，为25～45 MPa；而由于皮碗根部会挤入垫圈与缸套之间的间隙中，但根部径向变形后不足以与缸套接触，所以此处的接触压力为0。

图9 皮碗接触压力分布

图10所示为活塞皮碗与缸套接触面间摩擦应力云图和曲线图。可以看出，摩擦应力和接触压力的变化规律相似。摩擦应力最大值也出现在皮碗唇部边缘，为6～7 MPa，这是由于在皮碗唇部过盈量较大，皮碗唇部体积会被挤压，促使唇部边缘橡胶在有限距离内径向体积增大，而周围的直径会相应减小，导致皮碗唇部向其中心弯曲，边缘的摩擦应力变大，也在一定程度上反映了活塞皮碗存在向心效应。皮碗唇部由于存在向心效应，钻井液中磨粒会进入缸套与皮碗的接触面，可能发生磨损失效。

图10 皮碗摩擦应力分布

3.3 验证

为验证数值模拟方法的可行性，将图9中的仿真模拟结果与文献[18]实验结果进行对比，发现接触压力模拟结果与实验结果变化规律基本吻合。由于模型尺寸和压力大小有一定差别，所以实验结果与仿真结果有一定的误差，但总体的变化趋势是一致的，表明数值模拟方法的可行。

4 皮碗尺寸对接触压力的影响

接触压力作为判断密封性能的重要指标，接触压力越大，活塞能密封的介质压力越大。图11和图12分别示出了活塞皮碗在不同唇部过盈量λ和不同唇角θ下皮碗与缸套之间接触压力沿轴向的变化情况。

在51.7 MPa钻井液压力作用下，活塞唇部过盈量λ从0.5 mm增大到2.0 mm时，活塞皮碗与缸套接触面间接触压力的变化情况如图11所示。可以看出，当过盈量λ≤1.0 mm时，皮碗唇部接触压力从根部至唇部逐渐增大；过盈量λ>1.0 mm时，由于唇部过盈量大，变形量也更大，橡胶的松弛程度也会加剧，唇部橡胶将向中心弯曲，产生向心效应，导致唇部边缘后部橡胶在有限距离内径向体积增大，唇部边缘的接触压力也大于唇部接触压力。但总的来说，过盈量λ≤1.0 mm时，沿轴向的接触压力变化不大，对密封性能影响也不大；当λ>1.0 mm时，由于皮碗唇部存在向心效应，发生磨损失效的可能性增大，皮碗缸套的密封性能也会受到影响。

图11 不同过盈量时的接触压力曲线

图12显示了在51.7 MPa钻井液压力作用下皮碗唇角θ为15°～30°时，活塞皮碗与缸套接触面间接触压力变化情况。可以看出，唇角的变化会影响向心效应，当唇角θ≤15°时皮碗唇部不会产生向心效应，密封性能最好；当θ>15°时，皮碗唇部橡胶将向中心弯曲，产生向心效应，进而影响皮碗的密封性能。

图12 不同唇角时的接触压力曲线

5 结论

(1)一个周期内皮碗与缸套接触面之间的最大等效应力、接触压力和摩擦应力曲线变化规律同缸套内压力变化曲线相似，都随钻井液压力增大而增大，随压力的减小而减小。

(2)在最大钻井液压力作用下，缸套内表面和垫圈表面与皮碗接触部位等效应力都较大。后期改进设计时应重点考虑强化受力较大的部位。

(3)在最大钻井液压力作用下，皮碗受到应力都主要集中在活塞皮碗唇部和根部与垫圈接触的位置，也是皮碗易发生失效的2个部位，所以加强皮碗这2个部位将有助于活塞寿命的提高。

(4)当皮碗与缸套之间过盈量λ≤1.0 mm时，接触压力沿皮碗轴向分布规律相似，对密封性能影响不大；当过盈量λ>1.0 mm时，会导致皮碗唇部的接触压力小于皮碗唇部边缘处，产生向心效应，发生磨损失效的可能性增大，皮碗缸套的密封性能也会受到影响。

(5)当皮碗的唇角θ≤15°时，皮碗唇部不会产生向心效应，密封性能最好；当唇角θ>15°时，皮碗唇部橡胶将向中心弯曲，产生向心效应，进而影响皮碗的密封性能。