两类图的2-距离和可区别边染色

刘 欢，强会英*，白 羽，王洪申

（1.兰州交通大学 数理学院，兰州 730070；2.兰州理工大学 机电工程学院，兰州 730050）

图的可区别染色问题是图染色理论的一个分支，具有重要的理论意义和应用背景.2013年，Flandrin等［1］考虑了相邻顶点色集合的元素之和，首次提出图的邻和可区别边染色的概念，并给出一些特殊图的邻和可区别边色数.文献［2-5］在此基础上，研究了一些简单图的邻和可区别边染色问题.2021年，强会英等［6］在邻和可区别边染色的基础上进行了2-距离和可区别边染色的研究，得到无K4-子式图的2-距离和可区别边色数的一个上界.近几年，不少图论方向研究人员对蛛形图［7-8］和蛛网图［9-11］的各类染色问题做了大量的研究.本文在上述研究的基础上讨论了蛛形图和蛛网图的2-距离和可区别边染色问题，得到蛛形图、蛛网图的2-距离和可区别边色数.

文中讨论的图都是有限、无向的简单连通图，V（G）和E（G）分别表示图G的顶点集和边集，Δ（G）表示图G的最大度．令C=｛1，2，…，k｝为k-色集（k是正整数），C（vij）表示点vij的色集合，符号｛x1，x2，…，xn｝→｛a1，a2，…，an｝表示用颜色序列a1，a2，…，an去染元素序列x1，x2，…，xn，其它未加说明的术语，请参考文献［12-14］．

1 预备知识

定义1令f是图G的一个正常［k］-边染色，若对任意uv∈E（G），有S*（u）≠S*（v），其中S*（u）=则称f为图G的邻和可区别边染色［2］．染色中用到的最小k值称为G的邻和可区别边色数，记为

定义2令f是图G的一个正常［k］-边染色，若对任意u，v∈V（G），dG（u，v）≤2，都有S（u）≠S（v），其中，则称f为图G的2-距离和可区别边染色［6］．染色中用到的最小值k称为G的2-距离和可区别边色数，记为

定义3从v0出发有k（k≥3）条路，除v0外，每条路有k个点，共有n（n=k2+1）个点的图称为蛛形图［7］，记为Sk，它的头点用v0表示，删去v0后，这k条路分别记为pi=vi1vi2…vik（1≤i≤k），eij表示边vi（j-1）vij（1≤i≤k，1≤j≤k）．

定义4在蛛形图Sk中添加边v1jv2j，v2jv3j，v3jv4j，…，v（k-1）jvkj，vkjv1j（1≤j≤k-1）所得到的图称为蛛网图［9］，记为wk．

引理1对于简单图Δ（G）．若图G有相邻最大度点，则

引理2若简单图G在2-距离内有两个最大度点，则

2 主要结论

定理1对于蛛形图

证明根据蛛形图的结构，下面分两种情形去讨论．

情形1当k=3时，不存在相邻的最大度点，根据引理1知，．假设存在S3的2-距离和可区别3-边染色，设色集合C=｛1，2，3｝，则C（v0）=｛1，2，3｝，要满足正常的边染色且距离小于2的色集合和值不同，令f（v0v11）=1，f（v11v12）=2，则f（v12v13）=3，否则S（v11）=S（v12），又由边v11v12和边v12v13的色数不同且分别属于C（v11）和C（v13），此时S（v11）=S（v13）=3，出现矛盾，故不存在S3的2-距离和可区别3-边染色．

下面给出蛛形图S3的一个2-距离和可区别4-边染色：

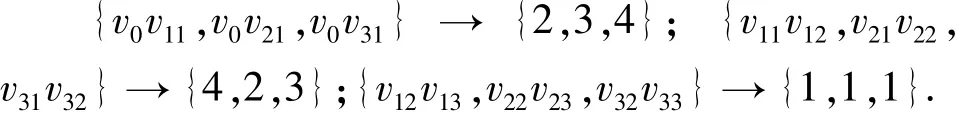
按上述染色法各点色集合与色数和如表1所列.

表1 图S3各点色集合C（vij）和色数和S（vij）的情况Tab．1 Sets of colors C（vij）and the chromatic number sum S（vij）of each vertex in Graph S3

从表1易见f是图S3的2-距离和可区别4-边染色.

情形2当k≥4时，不存在相邻的最大度点，根据引理1知

当k=4、5时，图S4、S5不适合下述染色方法，现给出S4、S5具体染色方法，如图1和图2所示．

图1 蛛形图S4Fig．1 Spider graph of S4

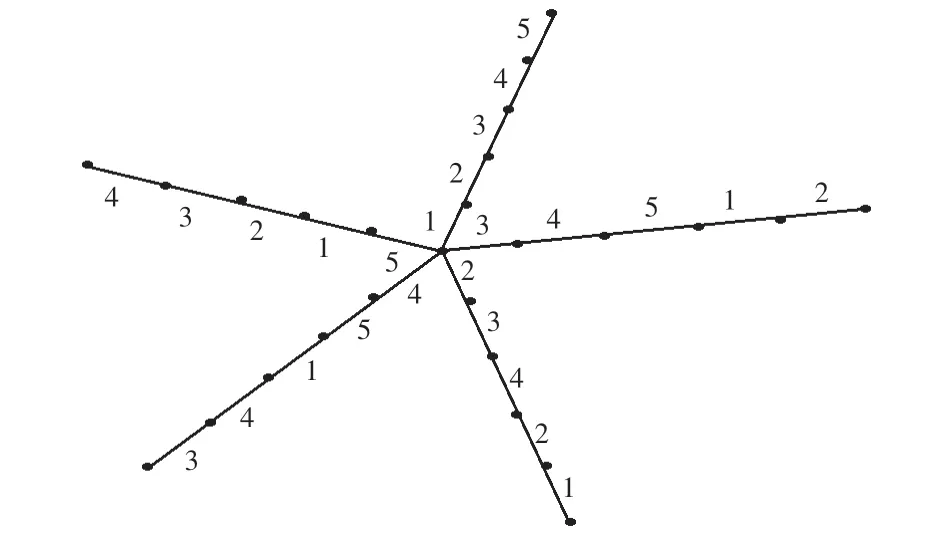
图2 蛛形图S5Fig．2 Spider graph of S5

当k≥6时，下面给出图Sk的一个2-距离和可区别k-边染色：

如下定义一个从E（Sk）→｛1，2，3，…，k｝的映射f，f（ei1）=i（1≤i≤k）；f（v11v12）=k-1；f（vi1vi2）=k（2≤i≤k-1）；f（vk1vk2）=1．

此时，C（v0）=｛1，2，3，4，…，k｝；C（v11）=｛1，k-1｝；C（vi1）=｛i，k｝（2≤i≤k-1）；C（vk1）=｛1，k｝．得到i+k；S（vk1）=k+1．

其它的边vijvi（j+1）（j≥2）分成如下两种情形讨论：

1）当k≡1（mod 3）时，各边染色情况分组讨论：

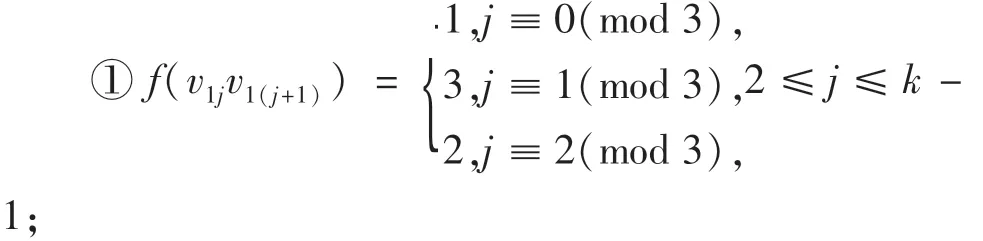
C（v12）=｛2，k-1｝；C（v1k）=｛1｝；C（v1j）依次按照｛1，2｝、｛1，3｝、｛2，3｝循环（3≤j≤k-1）．得到S（v12）=k+1；S（v1k）=1；S（v1j）按照3，4，5循环出现．

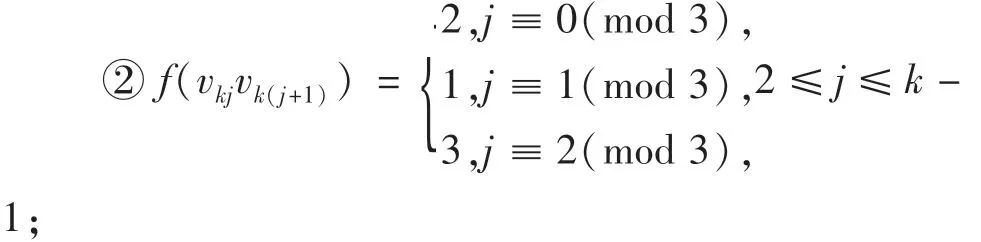
C（vk2）=｛1，3｝；C（vkk）=｛2｝；C（vkj）依次按照｛3，2｝、｛2，1｝、｛1，3｝循环（3≤j≤k-1）．得到S（vk2）=4；S（vkk）=2；S（vkj）按照5，3，4循环出现．

C（vi2）=｛1，k｝（2≤i≤k-1）；C（vik）=｛2｝（2≤i≤k-1）；C（vij）依次按照｛1，2｝、｛2，3｝、｛3，1｝循环（2≤i≤k-1，3≤j≤k-1）．得到S（vi2）=k+1（2≤i≤k-1）；S（vik）=2；S（vij）按照3，5，4循环出现．

由①②③知f是图Sk的2-距离和可区别k-边染色．

2）当k≠1（mod 3）时，各边染色情况分组讨论：

此时C（v12）=｛2，k-1｝；C（vk2）=｛1，2｝；C（vij）依次按照｛2，3｝、｛1，3｝、｛1，2｝循环（i=1，k；3≤得到S（v12）=k+1；S（vk2）=3；S（v1j）、S（vkj）按照5，4，3循环出现（3≤j≤k-1）；S（v1k）=S（vkk）=

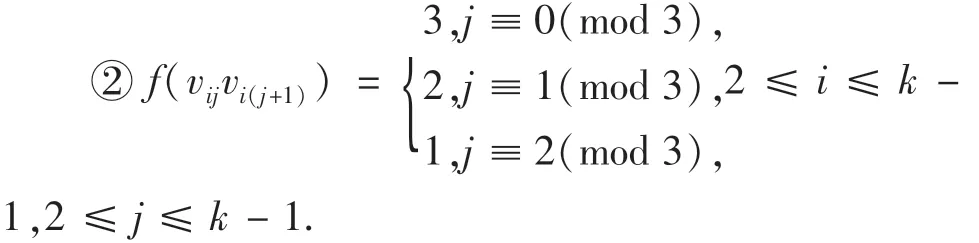
此时C（vi2）=｛1，k｝（2≤i≤k-1），C（vij）依次按照｛1，3｝、｛2，3｝、｛2，1｝循环（2≤i≤k-1，3≤得到S（vi2）=k+1（2≤i≤k-1）；S（vij）按照4，5，3循环出现

由①②知f是图Sk的2-距离和可区别k-边染色．

综上所述，此定理成立．

定理2对于蛛网图Wk（k≥3），则

证明根据蛛网图的结构，下面分3种情形去讨论．

情形1当k=3时，存在相邻的最大度点，根据引理2知，χ′2-∑（G）≥χ′∑（G）≥Δ（G）+1=5．

假设存在W3的2-距离和可区别5-边染色，设色集合C=｛1，2，3，4，5｝，以点v11为例，要满足正常的边染色且距离小于2的色集合和值不同，需与点v11相邻的点v12、v31、v21达到色集合和值不同，与点v11达到2-距离的点v22和v32，同样需要保证其2-距离和可区别边染色．由于C45=5，而蛛网图W3中存在6个4度顶点需要达到色集合和值不同．故不存在W3的2-距离和可区别5-边染色．

下面给出蛛网图W3的一个2-距离和可区别6-边染色f．

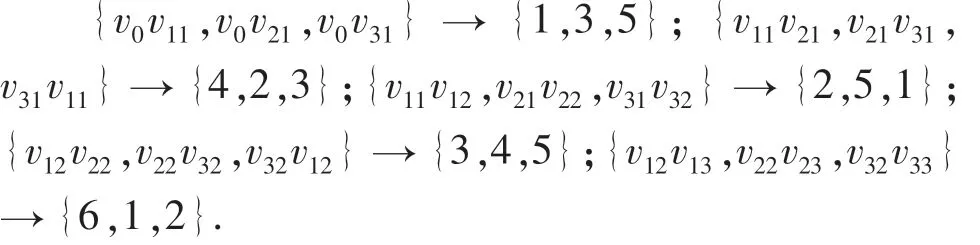
按上述染法各点色集合与色数和如表2所列.

表2 图W3各点色集合C（vij）和色数和S（vij）的情况Tab．2 Sets of colors C（vij）and the chromatic number sum S（vij）of each vertex in Graph W3

从表2易见f是图W3的2-距离和可区别6-边染色．

情形2当4≤k≤6时，分以下两种情况讨论：

①当k=4时，存在相邻的最大度点，根据引理2知根据情形1当k=3时可知，不存在W4的2-距离和可区别5-边染色．假设存在W4的2-距离和可区别6-边染色，设色集合C=｛1，2，3，4，5，6｝，以点v12为例，要满足正常的边染色且距离小于2的色集合和值不同，需保证与点v122-距离内的11个4度顶点色集合和值不同．由于色中选取4种元素其色集合和值有10，11，…，18共9种情况．蛛网图W4中2-距离内最多存在11个4度顶点需要达到色集合和值不同，9＜11．故不存在W4的2-距离和可区别6-边染色．

下面给出图W4的一个2-距离和可区别7-边染色f，如图3所示.

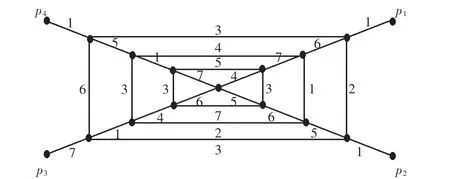
图3 蛛网图W4Fig．3 Spider web of graph W4

此时C（v0）=｛4，5，6，7｝，S（v0）=22．其余各点情况如表3所列，易见f是图W4的2-距离和可区别7-边染色．

表3 图W4各点色数和S（vij）的情况Tab．3 Chromatic number sum in Graph W4

②k=5，6时，图W5和W6均不存在2-距离和可区别6-边染色，理由同①k=4的情况，图W5和W6的一个2-距离和可区别7-边染色f如图4和图5所示．

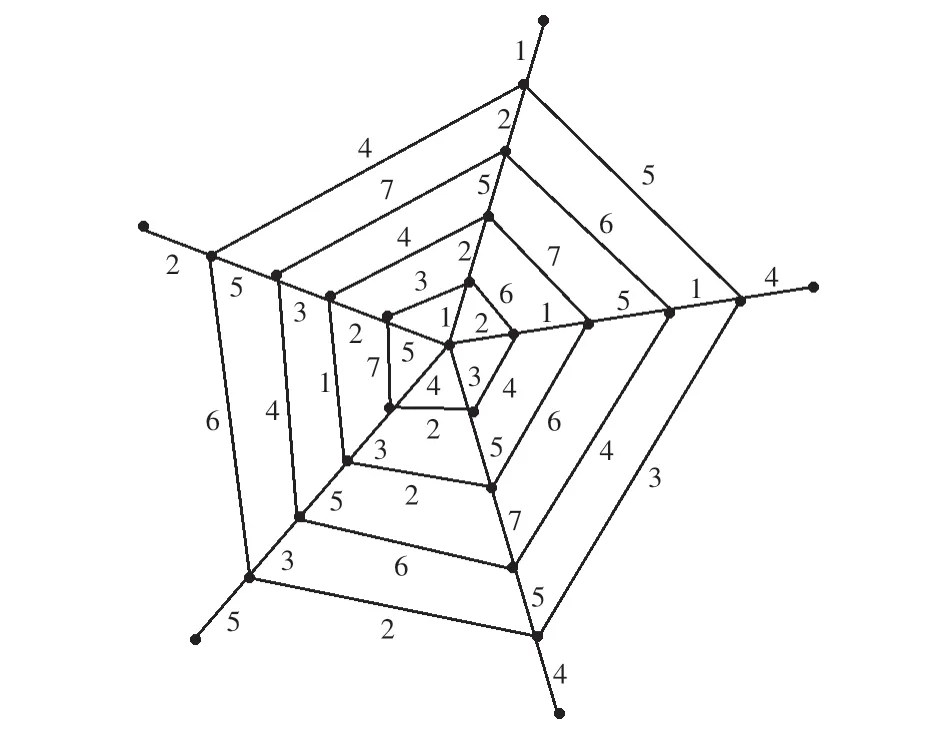
图4 蛛网图W5Fig．4 Spider web of graph W5

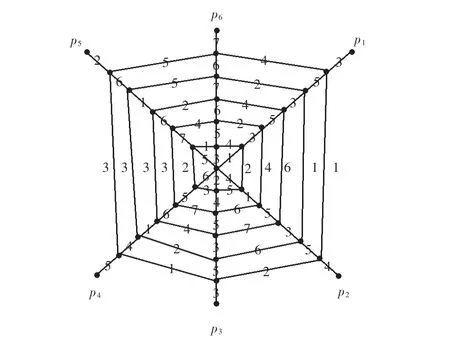
图5 蛛网图W6Fig．5 Spider web of graph W6

按上述染法蛛网图W5有C（v0）=｛1，2，3，4，5｝，S（v0）=15．蛛网图W6有C（v0）=｛1，2，3，4，5，6｝，S（v0）=21.其余各点情况如表4及表5所列.

从表4和表5易见f是图W5和W6的2-距离和可区别7-边染色.

表4 图W5各点S（vij）的情况Tab．4 Chromatic number sum in Graph W5

表5 图W6各点S（vij）的情况Tab．5 Chromatic number sum in Graph W6

情形3当k≥7时，不存在相邻的最大度点，根据引理1得．设色集合为｛1，2，3，…，k｝，图Wk中除叶子点vik（1≤i≤k）以及点v0之外，均为4度顶点，从色集合中选取4种元素其和值可能出现的数值为1+2+3+4=10，至k+（k-1）+（k-2）+（k-3）=4k-6，共有（4k-15）种和值情况．接下来对蛛网图Wk的路数k做归纳．

当k=7时，以点v12为例，要满足正常的边染色且距离小于2的色集合和值不同，需保证点v12与2-距离内相关联的共13个顶点色集合和值不同．其中v0点色集合为｛1，2，3，…，k｝，与其它4度顶点已保持不同．

图6 蛛网图W7Fig．6 Spider web of graph W7

假设对路数小于等于k-1的蛛网图Wk-1上述结论成立.

下证对于k条路的蛛网图，此结论依然成立．由归纳假设知，Wk-1存在2-距离和可区别（k-1）边染色φ．根据蛛网图Wk-1到Wk的结构特点，分成以下四种情况去讨论.

1）增加点v1k，v2k，…，vkk及边v1，k-1v1k，v2，k-1v2k，…，vk，k-1vkk．这些点全是叶子点，与其它4度顶点可达到2-距离和可区别边染色，且这些叶子点两两之间距离大于2，不妨令这些边色数分别从f（vi，k-1vi，k）=｛1，2，3，…，k｝-f（vi，k-2vi，k-1）中取得，故k色可满足这些叶子点2-距离和可区别边染色．

2）增加k条边v1，k-1v2，k-1，v2，k-1v3，k-1，…，vk-1，k-1vk，k-1，vk，k-1v1，k-1．以点v3，k-1为例，需保证与点v3，k-2，v3，k-3，v4，k-1，v4，k-2，v5，k-1，v2，k-1，v2，k-2，v1，k-1达到2-距离和可区别边染色．根据路数等于k-1的蛛网图Wk-1染色情况分析，v3，k-2，v3，k-3，v4，k-2，v2，k-2已达到2-距离和可区别边染色，去掉｛S（v3，k-2），S（v3，k-3），S（v4，k-2），S（v2，k-2）｝这4种和数情况下，并添加k色的基础上，使其余点达到2-距离和可区别边染色，共有（4k-15）种情况，在（C4k-4）种可能性中，使用k色足够使得蛛网图Wk达到2-距离和可区别边染色．

3）增加路pk上边v0vk1，vk1vk2，…，vk，k-1vk，k．在情况1、2的染色基础上，仅需考虑v0vk1，vk1vk2，…，vk，k-2vk，k-1，根据计算得，（k-1）色和k色相差（4k-15）-［4（k-1）-15］=4种．故可给pk路上点色集合和值赋予该4种情况，让该4种和值情况以一定顺序循环，不妨可以让S（vk1）=4k-9，S（vk2）=4k-8，S（vk3）=4k-7，S（vk4）=4k-6，…，与Wk-1的染色情况可达到和值不同，故达到2-距离和可区别边染色．

4）对于图Wk-1至图Wk中，因增加pk路造成pk-1和p1路间需重新染色，把Wk-1中pk路与p1路间相连的边颜色赋予给Wk中pk-1路和pk路间相连的对应边，对于pk路与p1路间的连边，①以点v12为例，与点v12相关联的4条边，在φ染色下有3条边色数已确定，现从k种色中去掉这3种颜色，给第4条边进行染色，在中有（k-3）种情况，故存在（k-3）种和值情况，点v12有12个4度点需要达到2-距离和可区别边染色，12+（k-3）≤4k-15，使用k色可达到2-距离和可区别边染色．②对于p1路上其他点，最多有13个4度点需要达到2-距离和可区别边染色，存在（4k-15）-13种和值染法，用k色可达到2-距离和可区别边染色．③其中当k≥10时，点v11为特例，有（k+4）个点需要达到2-距离和可区别边染色，（k+4）+（k-3）=2k-1，远小于（4k-15）种和值情况，从而达到2-距离和可区别边染色．

综上所述，图Wk满足2-距离和可区别k-边染色，定理成立．