独立不同分布的n中取（n-k+1）系统存活元件的剩余寿命

温九红

（兰州交通大学 数理学院，兰州 730070）

n中取（n-k+1）系统作为一种重要的冗余系统被广泛地应用于航空工业、武器制造和电气工程等领域．一个系统被称为n中取（n-k+1）系统当且仅当n个元件中至少有（n-k+1）个元件工作，所以n中取（n-k+1）系统的寿命可以用元件寿命的第k个顺序统计量来表示．最近几十年，国内外关于n中取（n-k+1）系统剩余寿命和休止时间的研究有很多［1-7］.

然而在实际生活应用中，大多数的n中取（n-k+1）系统都是由独立但不同分布的元件构成，这样的系统的结构和分布函数表达都较为复杂．2001年David［8］利用permanent函数给出了独立但不同分布元件的寿命可靠度函数，为研究独立但不同分布元件的剩余寿命和平均剩余寿命提供了一个非常有用的工具．近些年许多学者开始关注独立但不同分布元件构成的n中取（n-k+1）系统，并得到很多有用的结论．Sadegh［9］在元件是独立但不同分布情形下讨论了并联系统的条件剩余寿命（Xn∶n-t｜Xr∶n＞t）（r=1，…，n）；Zhao等［10］在元件是独立但不同分布情形下考虑了n中取（n-k+1）系统的剩余寿命（Xk∶n-t｜Xl∶n＜t＜Xl+1∶n）（1≤l＜k≤n）；Gurler等［11］在元件是独立但不同分布情形下研究了n中取（n-k+1）系统的剩余寿命（Xk∶n-t｜X1∶n＞t）（k=1，…，n）；Sadegh［12］在元件是独立但不同分布情形下讨论了n中取（n-k+1）系统的剩余寿命（Xk∶n-t｜Xr∶n＞t）（r=1，…，n）；Zhang等［13］在元件是独立但不同分布情形下考虑了有两个时间监控的条件下并联系统的剩余寿命（Xn∶n-t2｜Xr∶n＜t1＜Xr+1∶n，Xn∶n＞t2）（1≤r≤n）．

本文将研究由n个独立但不同分布元件构成的n中取（n-k+1）系统中可存活元件的剩余寿命（Xk∶n-t｜Xj∶n＜t）（1≤j＜k≤n）得到了该剩余寿命可靠度函数和平均剩余寿命函数的混合表达，并对可存活元件的剩余寿命进行了普通随机序比较．

1 可存活元件剩余寿命的混合表达

定理1．1对任意的1≤j＜k≤n和0＜x＜t有：

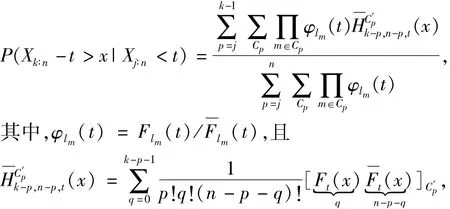
而集合Cp表示集合｛1，2，…，n｝中由p个元素构成的子集，集合为Cp的补集．

证明：对任意的1≤j＜k≤n和0＜x＜t有：

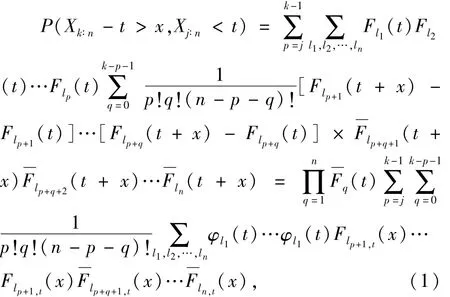
其中，l1，l2，…，ln是从1，2，…，n的所有排列，因此l1＜l2＜…＜lp，lp+1＜lp+2＜…＜lp+q，并且lp+q+1＜lp+q+2＜…＜ln．

再根据Permanent函数可将式（1）化简为联立式（2）～（3）可得到

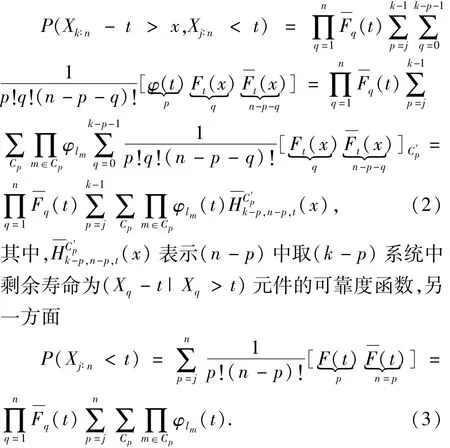
接下来将给出（Xk∶n-t｜Xj∶n＜t）的平均剩余寿命函数的混合表达．

定理1．2对任意的1≤j＜k≤n和0＜x＜t，则（Xk∶n-t｜Xj∶n＜t）的平均剩余寿命函数混合表达为

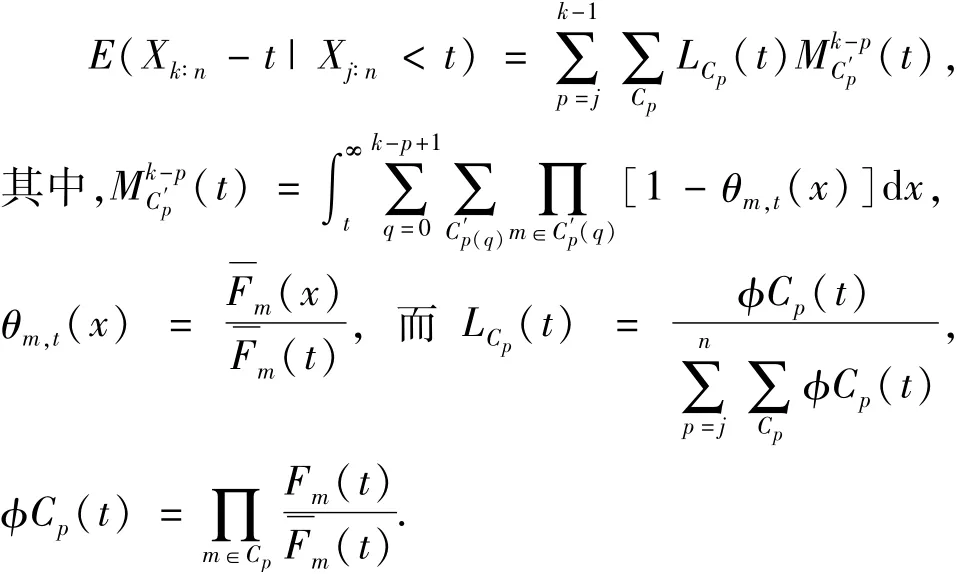
另外集合Cp表示集合｛1，2，…，n｝中由p个元素构成的子集，集合为Cp的补集，且集合表示基数为q的集合的子集．

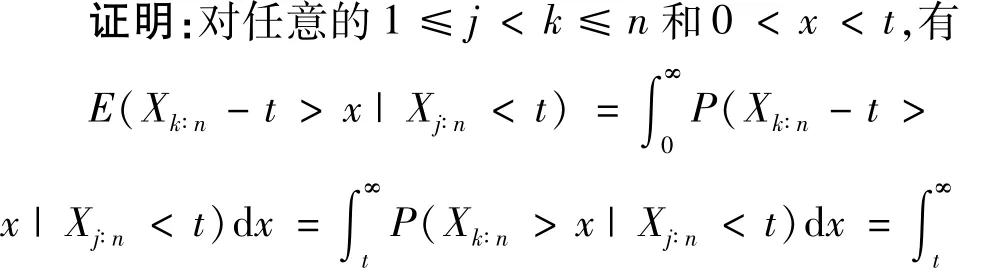
根据文献［9］有

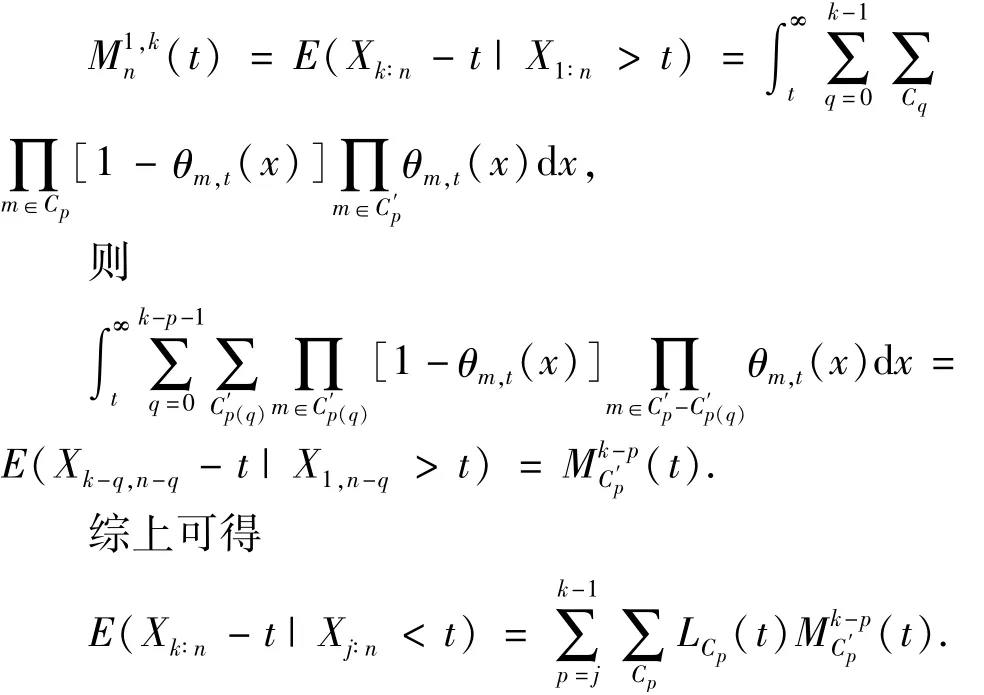
2 可存活元件剩余寿命的随机比较

引理2．1假设X1，X2，…，Xm和Y1，Y2，…，Yn是两组独立但并不一定同分布的随机变量．对任意的m，n和所有的i，如果Xi≤stYi，那么Xi∶m≤stYj∶n，其中i≤j，m-i≥n-j［14］．

定理2．2对任意的1≤j＜k≤n和0＜x＜t，有P（Xk∶n-t＞x｜Xj∶n＜t）≤stP（Xk+1∶n-t＞x｜Xj∶n＜t）．

证明：对于0＜x＜t和任意的1≤j＜k≤n，有式（4）分子等价于

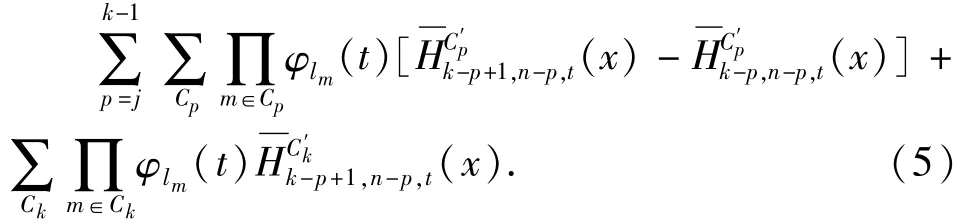
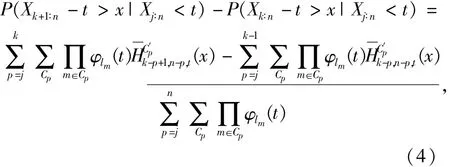
集合Cp的序列为（l1，l2，…，lp），补集相对应的序列为（lp+1，lp+2，…，ln）．根据引理2．1则有则式（5）大于零，故得证．

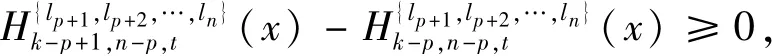
定理2．3对任意的1≤j＜k≤n和0＜x＜t，有

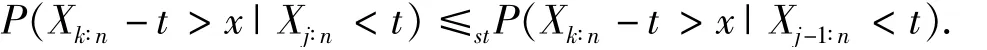
证明：对于0＜x＜t和任意的1≤j＜k≤n，有

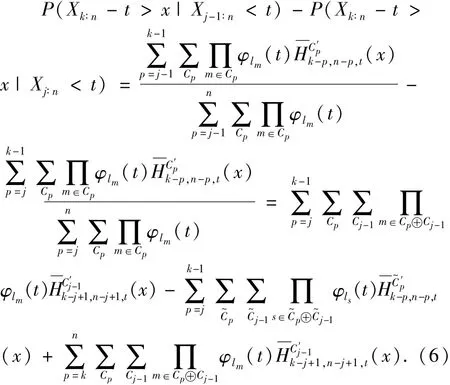
定理2．4对任意的1≤j＜k≤n和0＜x＜t，有

P（Xk∶n-t＞x｜Xj∶n＜t）≤stP（Xk∶n-1-t＞x｜Xj∶n-1＜t）．

证明：对于0＜x＜t和任意的1≤j＜k≤n，有

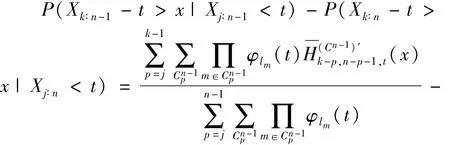
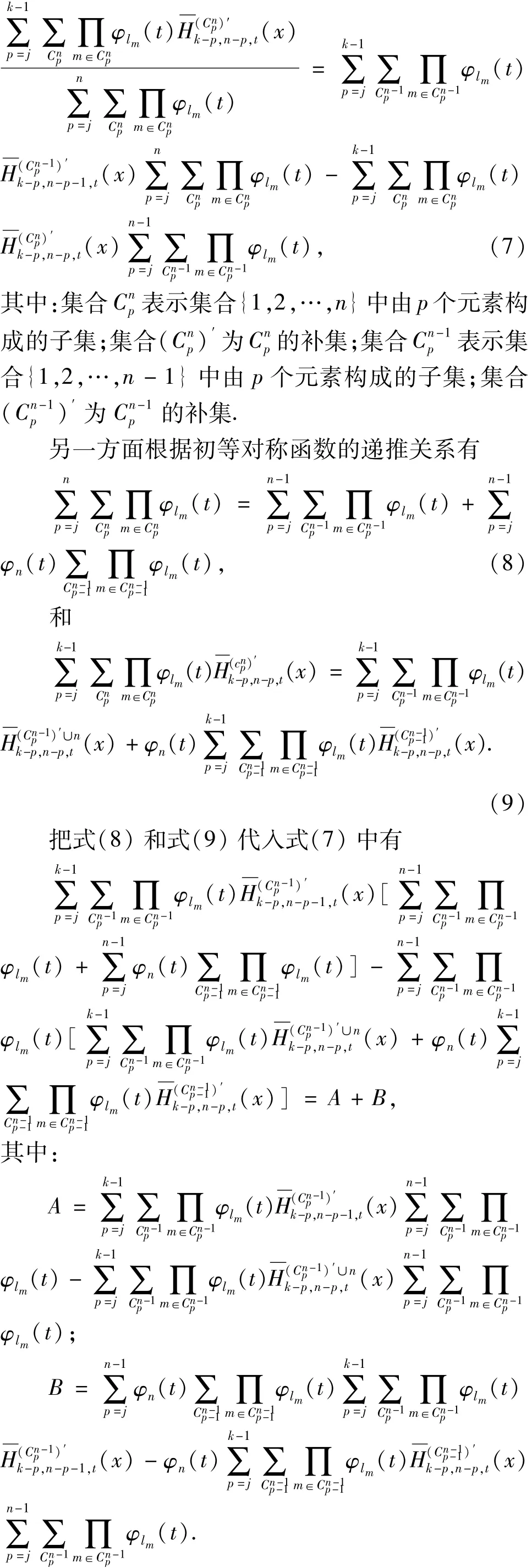
而A式又等价于

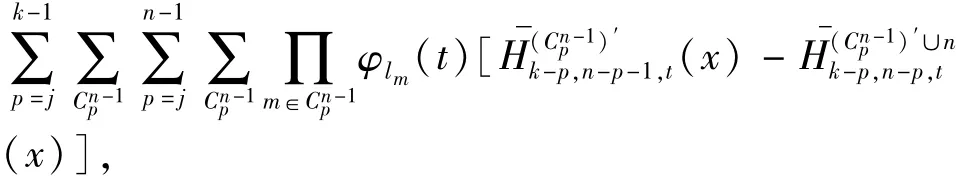
另一方面B式等价于

所以B式也非负，故得证．