基于张量奇异值分解的鲁棒视频水印算法

黄江涛 ,孙辛烨 ,马叶灵* ,杜 萌

（1.宁波大学科学技术学院,浙江 宁波 315300;2.宁波大学 信息科学与工程学院,浙江 宁波 315211）

随着互联网和计算机技术的快速发展,数字多媒体得到了广泛应用.为满足人们娱乐活动的需求,网上视频越来越多,内容也越来越丰富.然而,随之而来的安全隐患也越来越多,例如视频被非法篡改、下载以及复制等.如何有效地保护视频的版权成为了一个亟待解决的问题[1-2],而数字水印技术为视频的版权保护提供了有效途径[3-6].

视频水印根据变换域可分为基于空域的水印和基于频域的水印.基于空域的视频水印直接修改图像的像素值来实现水印的嵌入[7-8].空域视频水印计算简单,但是较容易在图像攻击下丢失水印信息,鲁棒性较差,主要用于篡改检测.相比基于空域的视频水印,基于频域的视频水印可以抵抗各种恶意攻击,具有较好的鲁棒性[9-10].该类算法通常首先将视频转换为频域,然后通过修改频域中的系数嵌入水印,常见的频域变换方式有离散余弦变换(Discrete Cosine Transform,DCT)、离散小波变换(Discrete Wavelet Transform,DWT)、奇异值分解(Singular Value Decomposition,SVD)等[11-12].Nguyen等[13]提出了一种基于DCT的视频水印算法,该算法将灰度水印分解为位平面,然后利用奇偶量化将水印嵌入到视频帧亮度分量的DCT 低频系数.Thanh 等[14]将水印图像嵌入到DCT 系数,并利用KAZE 特征自适应检测嵌入和提取的水印区域.Preda 等[15]将水印嵌入到视频帧的高频子带(HH)和中频子带(HL、LH)的小波系数中,从而实现水印鲁棒性.此外,在此基础上,Preda 等[16]通过扩频和量化相结合,将水印嵌入DWT 中频子带的小波系数,以提高水印鲁棒性.Bhardwaj 等[17]利用原始视频帧数、块的大小和嵌入容量之间的关系来确定关键帧的帧数,并对关键帧进行提升小波变换(Lifting Wavelet Transform,LWT),最后将水印嵌入低频子带(LL),从而实现鲁棒性.相比单变换,混合变换更能够提取视频的主要特征,从而增强水印的鲁棒性.Faragallah等[18]提出了一种基于SVD和DWT的视频水印算法,首先将视频帧进行DWT 变换,并将提取的HH、HL 和LH 进行SVD,最后将水印嵌入到相应的对角矩阵.熊祥光等[19]提出了混合整数小波变换和SVD 的视频水印算法,将水印嵌入最大奇异值.Sathya 等[20]利用场景变换检测提取视频的关键帧,进行DWT和SVD 的混合变换提取鲁棒特征,并嵌入水印.除了鲁棒性,郑秋梅等[21]则提出一种均衡特征的动态视频水印算法来提高水印的嵌入容量.

上述视频水印算法只是将视频当作连续的静止图像,并没有考虑到视频时域的相关性.视频既具有多维度特点,时域间又具有强相关性,因此若只是对某一帧提取特征,则将忽略视频帧间的强相关性,导致不能较好地抵抗视频特有的攻击,例如帧丢失、帧交换、H.264 和MPEG-2 等.Zhang等[22]提出了一种基于张量分解的视频水印的算法,该算法将视频看作一个三阶张量,然后对视频进行张量分解,利用奇偶量化实现水印的嵌入,但该算法对H.264 和MPEG-2 等攻击鲁棒性较差.

为了更好地保护视频的版权,多个连续帧将被看作高阶张量.由于张量奇异值分解(Tensor-Singular Value Decomposition,T-SVD)能够较好保留视频帧内的相关性和时域的相关性,本文由此提出一种结合T-SVD 的鲁棒视频水印算法,利用T-SVD 将视频分为2 个正交张量和1 个对角张量,对图像进行分块,并对每块进行T-SVD 分解,计算得到的对角张量.最后,将彩色图像水印的对角张量嵌入到视频的对角张量,从而实现水印嵌入.

1 背景知识

1.1 张量

1.1.1 张量的定义

随着互联网的发展,多媒体数据正朝着多维的方向发展.张量是多维数据的一种表现形式,它能够存储大量的信息.设P阶张量表示为:

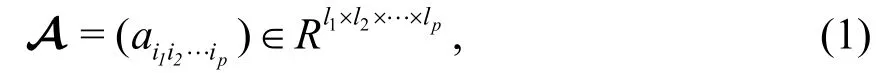
其中,l1,l2,…,l p∈Z代表每个维度元素的数量.采用一组矩阵表示为高阶张量,例如,三阶张量分为前向切片、水平切片和横向切片,分别表示为,其中k∈ {1,2,3}.

1.1.2 张量相关操作

首先为循环矩阵的计算.当向量的第一列被指定时,该向量能够被转换为循环矩阵[23].设向量,则转换的循环矩阵为:

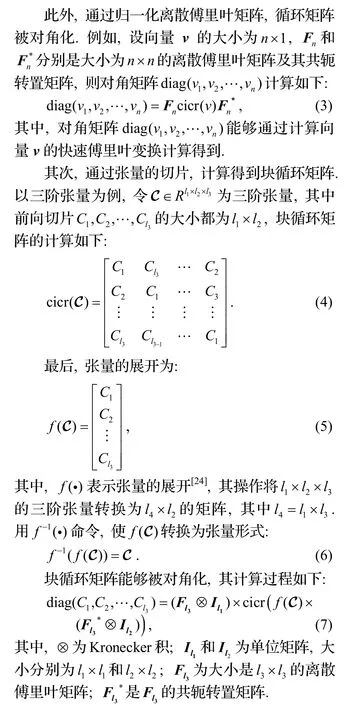
1.2 从SVD 到T-SVD

SVD 是线性代数中一种重要的分解技术,将1个二阶矩阵分解成2 个正交矩阵和1 个对角矩阵.

设B∈Rm×n为图像矩阵,进行SVD 运算,将B进行分解:

其中,U∈Rm×m和V∈Rn×n为正交矩阵,S∈Rm×n为对角矩阵,其对角线上的值为B的奇异值.

二阶矩阵被认为二阶张量,而高阶矩阵则被认为高阶张量,则需要高阶奇异值分解.T-SVD 是一种比较有效的高阶奇异值分解方法.以三阶为例,令为三阶张量,定义为:

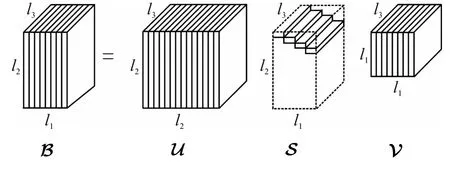
图1 T-SVD 结构图

2 基于张量奇异值分解的视频水印算法

将视频进行T-SVD,计算得到2 个正交张量和1 个对角张量.由于对角张量的奇异值包含了视频的主要能量,因此将其进行修改,进而嵌入鲁棒水印.如图2 所示,首先,确定选择视频的帧数,并提取视频帧.其次,对视频帧分别进行DWT 变换,并提取每帧的低频子带(LL).然后,为保留视频时域之间的强相关性,将每3 帧的LL 看作一个三阶张量,并进行分块.最后,对每视频块进行T-SVD变换,得到对角张量,并嵌入水印.水印的提取则为水印嵌入的逆过程(图3).

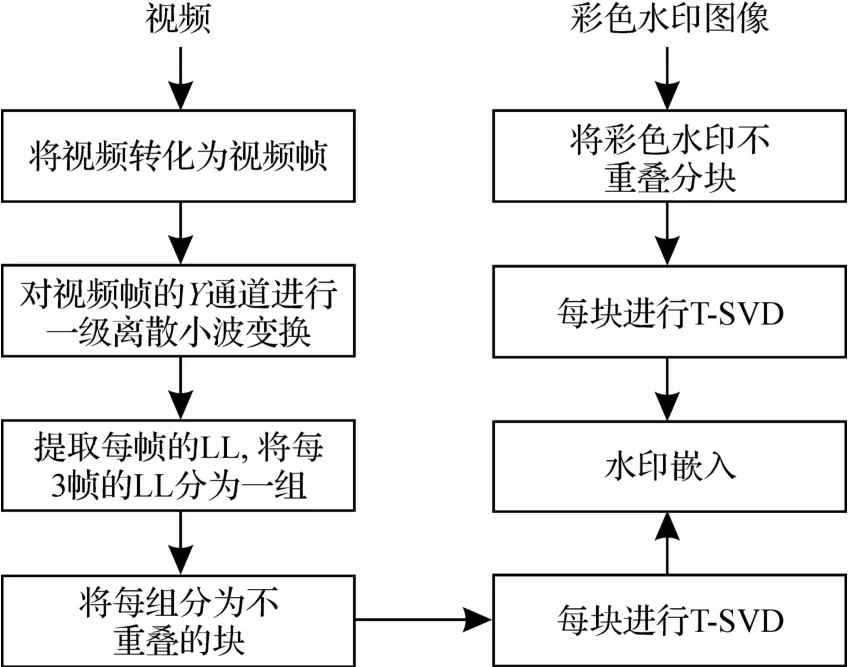
图2 水印嵌入

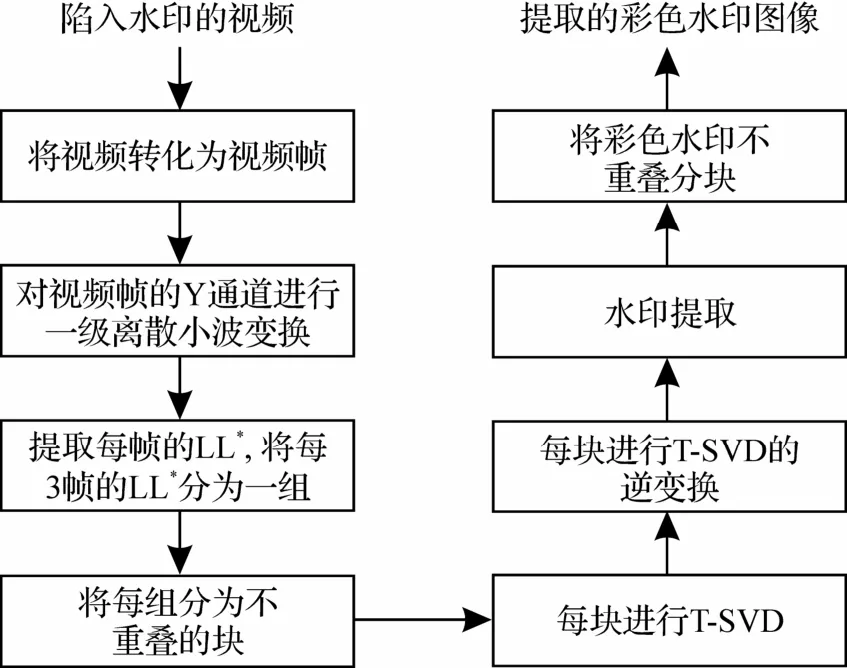
图3 水印提取

2.1 水印嵌入过程

设视频的大小为M×N× 3,彩色图像水印的大小为m×n× 3,水印的嵌入过程具体如下:

步骤1根据原始视频帧数、块的大小和嵌入容量之间的关系计算用于嵌入水印的视频帧数.

其中,Fs为M×N,Ws为m×n,Bs为a×b.

步骤2为了水印安全性,采用秘钥k随机提取RNF个视频帧用于嵌入水印,这些视频帧被命名为嵌入帧.提取嵌入帧的Y通道,并对Y通道进行一级DWT 变换.

步骤3提取每个嵌入帧的LL,并将每3 帧的LL 分为一组,当作一个三阶张量K,其大小为(M/2) ×(N/2) × 3.

步骤4将K 分为大小为a×b× 3的不重叠块Yj,并对每块进行T-SVD 分解.

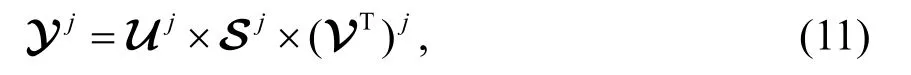
其中,j为每块的索引.

步骤5将彩色水印分成大小为r×t× 3的不重叠分块 Qj,其中a=r,b=t.

步骤6将第j块彩色水印 Qj嵌入到 Sj中.

其中,∂为嵌入强度.

步骤7对 Tj进行T-SVD 分解:

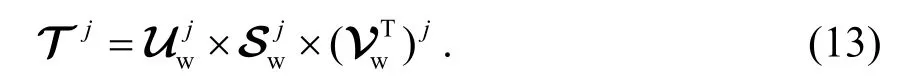
步骤8进行T-SVD 的逆变换,得到含水印的块:

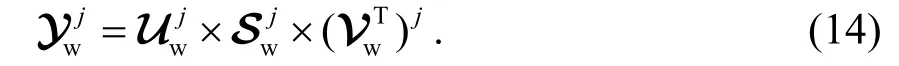
步骤9得到含水印的LL,并进行一级DWT逆变换,从而得到含水印的视频帧.重复步骤,直至所有视频块被嵌入水印.

2.2 水印提取过程

步骤1提取含水印帧的Y通道,并对Y通道进行一级DWT 变化.

步骤2提取每帧的低频子带LL*,并将每3 帧的LL*分为一组,当作一个三阶张量 K*.

步骤3将 K*分为不重叠的块 Y*j,大小为a×b× 3,并对每块进行T-SVD 分解.

步骤4进行T-SVD 逆变换得到 T*j:

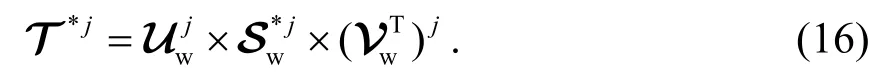
步骤5计算得到彩色图像水印块 Q＊j:

步骤6将彩色图像块组合在一起,提取彩色图像水印,从而确认视频版权.

3 实验结果与讨论

使用Freman、Akiyo、Mother and Daughter 和Mobile 视频序列对本文算法进行测试,其大小为352×288×3,共计300 帧,块的大小为8×6×3.彩色水印Candy 和Tree 的大小为176×144×3,选择视频帧数为24 帧.图4 和图5 分别显示了测试视频序列和彩色水印图像.归一化相关系数(NC,变量名RNC)用于评估提取的原始水印与原始水印之间的相似性,即鲁棒性为:

图4 测试视频序列

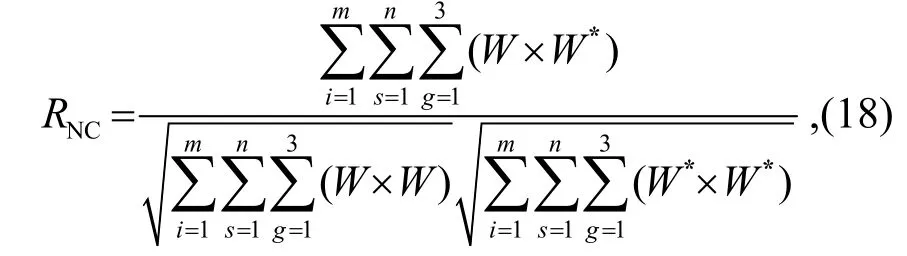
图5 彩色水印

其中,W和W*分别为原始水印图像大小和提取的水印图像大小,m×n为水印图像的大小.采用峰值信噪比(Peak Signal to Noise Ratio,PSNR)用于评估原始视频和含水印的视频之间的相似性,以及检测水印不可感知性.

3.1 不可感知和鲁棒性

彩色水印Candy 嵌入到视频序列Freman 和Mother and Daughter,它们的PSNR 分别为38.22 dB和38.91 dB,彩色水印图像Tree 嵌入到视频序列Akiyo 和Mobile,它们的PSNR 分别为38.31 dB 和37.56 dB.图6 显示了视频在没有任何攻击下提取的彩色水印,相应的NC 值都接近于0.99.因此,显示了算法的有效性.

图6 从不同视频提取的彩色水印

为证明所提出视频水印算法的鲁棒性,对视频序列进行不同攻击,例如椒盐噪声、高斯噪声、JPEG 压缩、滤波、帧交换等.在不同的攻击下,提取水印的NC 值实验结果见表1,由表中数据可见,提取水印的NC 值都高于0.8,证明水印具有较高的鲁棒性,从而可以有效地保护视频版权.其主要原因是本算法采用的T-SVD 能保留视频帧间的相关性,从而增强水印的鲁棒性.

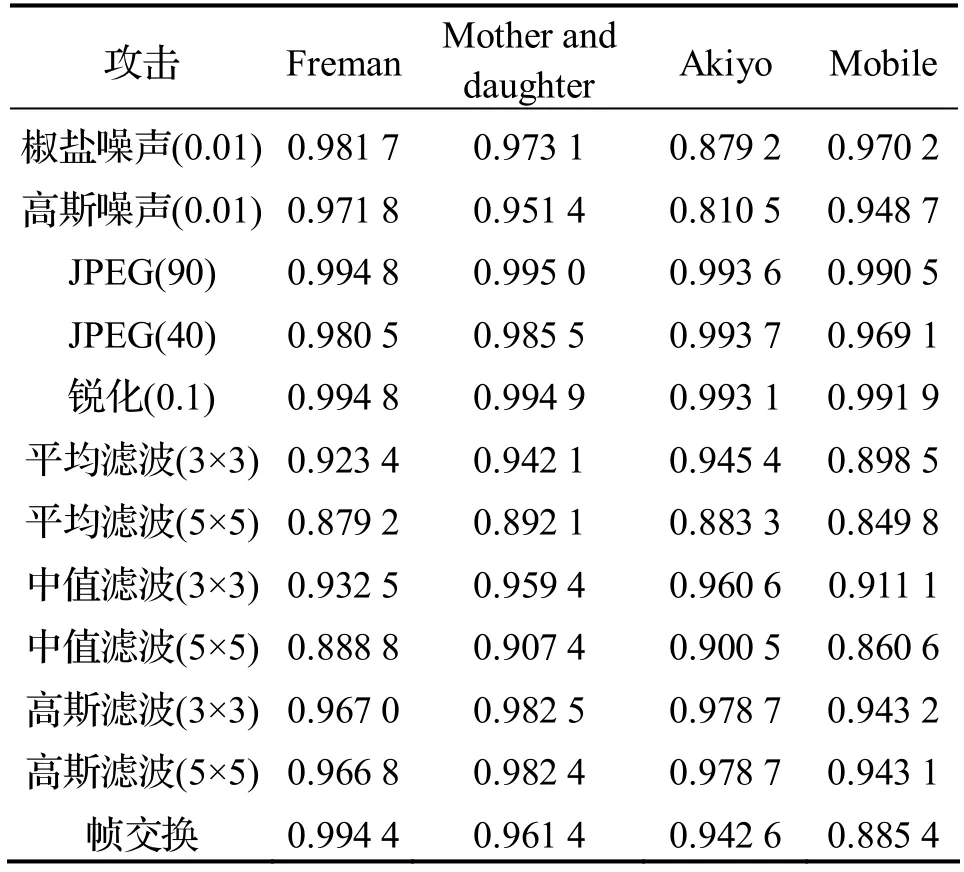
表1 不同攻击下,彩色水印图像嵌入到视频序列的NC 值

3.2 对比实验

为证明本文算法的鲁棒性,分别与文献[9]和文献[20]进行比较.从表2可知,大部分本文算法提取的NC 值优于文献[9]和文献[20],尤其是高斯噪声(0.01)、平均滤波(3×3)以及平均滤波(5×5).例如,在高斯噪声(0.01)攻击后,提取的NC值要比文献[9]的NC 值高0.2,并比文献[20]的NC 值高0.1.尽管当视频受到中值滤波(3×3)攻击后,本文算法提取的NC 值要比文献[9]的NC 值低0.1,但是在受到H.264 攻击后,本算法提取的NC 值明显高于文献[9]和文献[20].从表2 中还可以看出,本算法提取水印的NC 平均值要高于文献[9]和文献[20].因此,实验结果证明本文算法的鲁棒性优于文献[9]和文献[20].

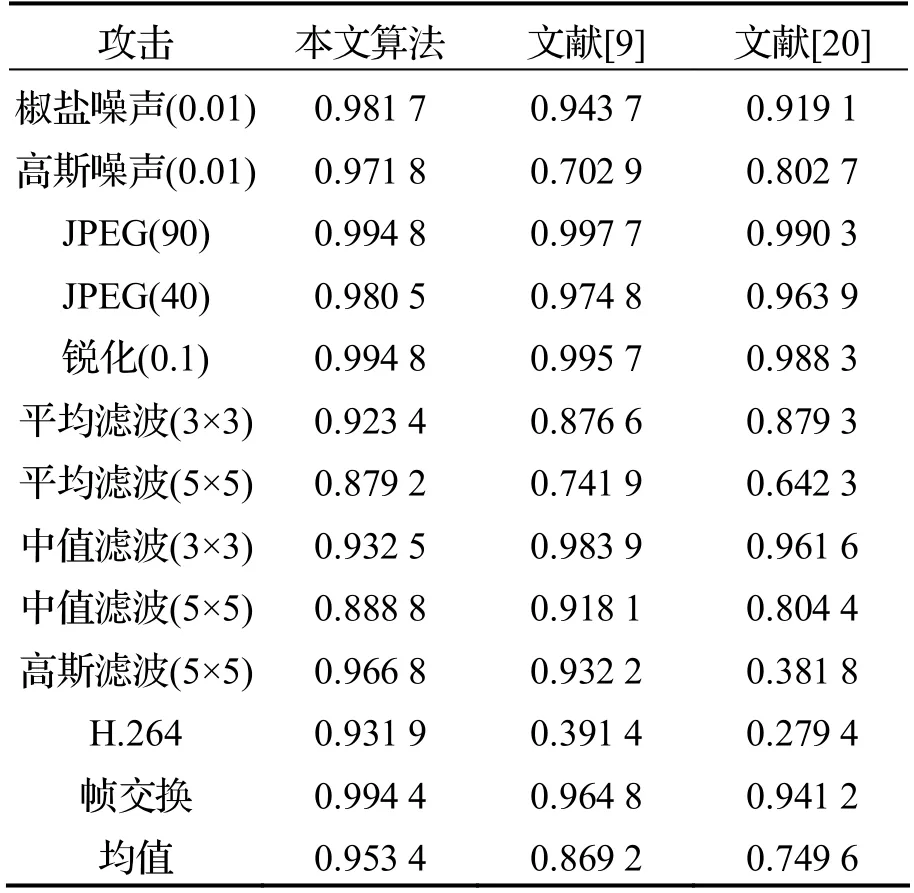
表2 受攻击视频序列Freman 中提取彩色水印图像Candy 的NC 值

图7 显示了从受到不同攻击的Freman 中提取的彩色水印图像Candy.从图可知,提取的水印图像可全部被识别,并具有较高的NC 值.

图7 从受攻击视频序列Freman 提取彩色水印图像Candy

图8 显示了从受攻击的Akiyo中提取的彩色图像水印Tree.从图可知,提取的水印能表明视频的版权信息,能够较好地保护视频的版权,该实验进一步证明本算法的鲁棒性.

图8 从受攻击视频序列Akiyo 提取彩色水印图像Tree

表3 为在Akiyo 提取的水印,当视频受到平均滤波(5×5)攻击下,本文算法提取的NC 值比文献[20]高0.3.虽然在泊松噪声和乘性噪声攻击后,本文算法提取的NC 值略低于文献[9]和文献[20],但考虑在不同攻击下的NC 平均值,本文算法明显高于文献[9]和文献[20].因此,综合以上实验结果,本文算法具有较高的鲁棒性,也具有较好的版权保护性能.

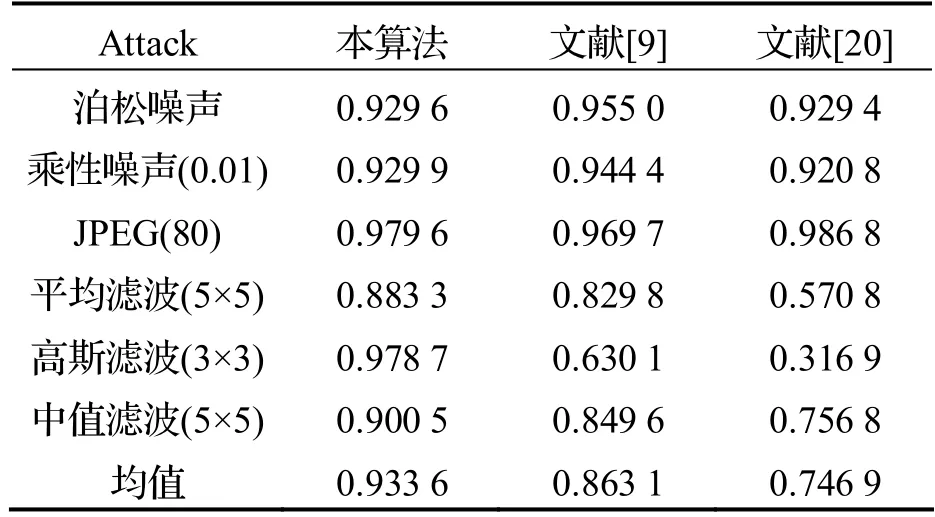
表3 从受到攻击视频序列Akiyo 中提取彩色水印图像Tree

4 结论

本文提出一种基于张量奇异值分解(T-SVD)的视频水印算法.利用视频多维度的特点,将视频看作一个高阶张量,通过T-SVD 保留视频帧之间的强相关性,从而保证水印的鲁棒性.由于对角奇异值包含了视频的主要能量,因此通过修改张量对角奇异值进行水印嵌入,提高了水印鲁棒性.此外,为了提高水印安全性,采用秘钥获取视频帧.实验结果表明,本文算法鲁棒性好于现有算法.然而对于平均滤波,本文算法相应的水印提取方法仍具有一定局限性,在将来的工作还需进一步改进.