探究“四维度”教学法培养小学生数学高阶思维能力

谢惠密

探究“四维度”教学法培养小学生数学高阶思维能力

谢惠密

（福建省厦门市海沧区芸美小学，福建厦门361026）

本文基于核心素养培养视角，笔者结合个人教学案例，从改进教学过程、突破教学环节、丰富学生经验三个维度进行逐一探究，仅供参考。

小学数学；高阶思维；教学法

在素质教育理念下，不仅要培养学生的综合品质，同时通过对深度学习理念的开发进一步发展学生的高阶思维拓展，培养学生的数学学科素养。笔者结合个人教学实践，以三个教学案例为例，从改进教学过程、突破教学环节、丰富学生经验三个维度入手，为“以深度学习助力学生高阶思维能力培养”的教学提供实践参考。

一、“三个明白”，改进教学过程

一是“活明白”，生活经验生长概念。以人教版四年级上册《速度、时间和路程》为例，通过“片段1：2分钟，小狗跑30米，小猫跑20米。”“片段2：小狗2分钟跑30米，小猪3分钟跑30米。”可以有效唤醒学生关于游戏、赛跑等生活经验，让学生在“活明白”的经验中熟悉“路程”“时间”等概念，并通过引导学生感悟赛跑的快慢即速度，以及速度与路程和时间的关系，实现学生生活经验到学生新知识概念的生长。

二是“想明白”，改造经验发展概念。“想明白”就是学生主体将其原有生活经验或已有的知识经验与新知识进行融合的过程。在片段1-2的基础上，通过“片段3：小狗2分钟中跑30米，小牛4分钟跑40米。”的呈现，让学生在“活明白”的基础上继续寻找生长点，通过知识的自主迁移、思维拓展，并对经验进行改造成功实现“想明白”，理解“先把时间和路程按比例改成时间相同时、再比较路程”，以及按比例改写路程、时间的必要性，还能初步感知公倍数与公因数的相关知识，实现新旧知识的无缝链接。板书设计如下图：

三是“学明白”，总结经验建构模型。杜威指出：教育就是经验的改造或改组。在学生明白“相同时间比较路程或相同路程比较时间”“按比例的把不同时间或路程改写成相同时间比较路程或按比例改写成相同路程比较时间”的基础上，教师可以通过“片段4：这么多种比法，你会选择哪种方法来比较？”引导学生想明白“比较1个时间单位的路程更方便”这个道理，进而实现将“1个时间单位的路程进行改造成‘速度’”的建模过程，并将建模过程总结如下：1分钟、1小时、1秒钟这样的1个时间单位的路程，叫速度。速度可以用路程除以时间求出来，公式：路程÷时间=速度。常用的速度单位有“米/秒”“米/分”“千米/时”等。

二、“三个针对”，突破教学环节

一是前置学习，打造真课堂。以人教版三年级下册《年、月、日》为例。教师通过设置课前预习单，引导学生养成自主学习习惯，也为实现高效课堂、打造真学习课堂奠定坚实基础。

二是基于困惑，开展真学习。学生的困惑处即为学生能力生长点。教师要营造轻松的教学氛围，让学生敢于提问、大胆质疑，展现已知、暴露未知，提出困惑。课上，在学生汇报交流并梳理出年、月、日的有关知识后，教师有意识地引导学生提出困惑：“为什么一年有时365天，有时366天？”“为什么一个月有28天、29天、30天，还有31天？”通过学生的小组学习、交流讨论，解决真困惑，实现真学习。

三是经历过程，实现真发展。《新课标》指出，学生要积极参与到学习活动中，亲身经历知识的形成和发展的过程，才能在掌握知识技能的同时，获得经验的积累和能力的发展。本节课学生通过课前自学，了解新知识，通过课中交流分享，形成知识网络。在学生问题解困环节，教师要耐得住性子，等得到花开，可以通过微课视频介绍“一年大约有365天5时48分46秒”展示年历，揭示平年、闰年规律，动手计算明白“四年一闰”等多种方式，让学生充分经历知识的形成和发展过程，完成知识建构，积累活动经验，实现自学能力、合作能力、表达能力、探究能力等全面发展意义上的真发展。

三、“三个改造”，丰富学生经验

一是唤醒和激活初始的经验。学生的学习是在现有经验的基础上，通过活动与体验不断形成新的知识经验。学生的现有经验是学生开始学习的现实基础，更是教师实施教学的重要资源。以人教版三年级下册《认识面积》为例，教师从中国地图入手，让学生找出青海省与福建省，并说说有什么发现。大部分学生发现“青海省的面积比福建省大”。通过让学生对面积的定义进行探索发现，唤醒、激活学生的现实体验，形成自然、合理的知识勾连，进而生成新的认知经验。

通过教师的引导和点醒，让大部分学生顺利地将面积的定义转化成新知识的“明白”。学习《认识面积》这节课之前，相信学生会有自己的“明白”。他们在生活经验中会听说过“面积”这个词，但在教学前测时，学生对面积的定义是模糊的，多数学生认为面积是东西的大小。但是学生对“面”是熟悉的，因为他们每天都接触“面”，每天都能摸到“面”，这些是学生的“明白”。教师把学生的这些“明白”唤醒与激活：这些面的大小是就面积。把学生的“明白”与新知识进行联系，新教学的知识就会扎根于学生的已有认识，自然生长。

二是区别与排除干扰的经验。以二年级上册《角的初步认识》为例，教师通过从“1角、牛角、羊角、桌角……”等生活化的“角”的概念入手，让学生找角、画角、认知角、定义角，学会区分“牛角、羊角”及“元、角、分”等角的日常概念与数学概念，经历对比、分析过程，辨析错误概念、排除干扰信息，实现知识与生活的畅享联通，构建正确的数学概念。

教学二年级上册《角的初步认识》一课时，学生对角并不陌生，课堂开始，学生的角是生活日常概念：1角、牛角、羊角、桌角……

师：请大家找一找，剪刀、时钟、红领巾上面的角（见下图）。

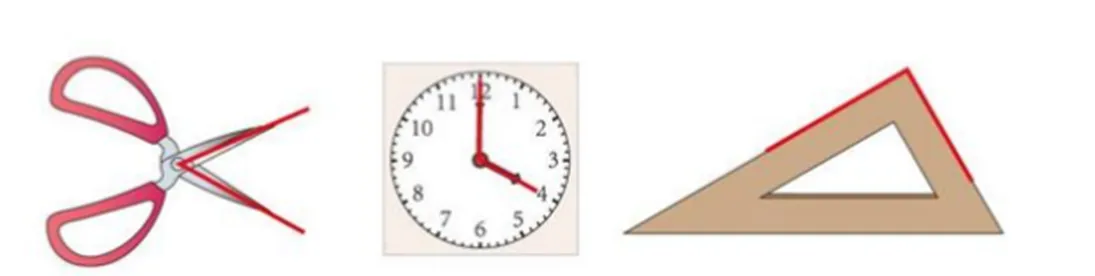
师：在学习单上，画出你找到的角。

师：比一比，哪个角画得好？

师：用什么词说说你画的角有什么特点？

……

让学生通过师生互动、生生互动，结合生活器具的对比、认知及课堂实操，进一步明晰“角”的概念。

学生对角的“明白”是“元、角、分”的“角”，“牛角”“羊角”，他们的“明白”与数学概念的“角”这个数学知识存在不一致，甚至干扰新知识的建构。“桌角”这个生活概念也起到干扰作用，多数学生认为桌角不是角，因为桌角的四个角都是弯弯的，而数学概念的“角”的顶点部分是尖尖的。在这里，教师要把桌角的“角”与数学概念的“角”进行对比与分析，让学生进行思辨，把学生的“明白”与教师的“明白”进行区别与联通，使学生的新的数学知识强于已有的生活经验，最后构建正确的数学概念。

三是改造与利用负面的经验。学生现有的生活经验、知识经验，有时会促进学习，有时会阻碍学习。教师如何合理运用、妥善解决显得尤为重要。以六年级上册《比的认识》为例，学生认识的“比”主要是比赛的比分，是差比关系，而本节的重点是数的倍比关系。学生旧经验对课堂新内容产生负面效应，需要教师正视问题，充分准备，巧妙应对，才能达到科学改造、高效利用的教学效果。

教学六年级上册《比的认识》一课，学生的“明白”是比赛的“比”，这个“明白”会对新知识的掌握起到负面作用。数学的“比”是倍比关系，而比赛的“比”是差比关系，学生的这个理解会对“比”的知识内涵起到副作用。但是教师不能绕过学生的理解，直接教学新知识，而是要利用学生的理解与新知识的理解进行充分对比，让学生深刻感受两种“比”的内在与区别，这样对学生的知识结构起到有益作用。

学生的学习是对已有的经验通过各种活动和体验改造成新的知识经验。而教师在教学新知前，不仅要备学习的知识内容，还要备学生的理解，并能甄别和筛选学生的这些理解，以这些理解为基础，找到学生接受新知识的一个突破口，巧妙地把学生的理解改造成新知识的理解，最后构建正确的数学概念。

四、三个“聚焦”，促进教学生成

一是聚焦知识结构化。结构化学习致力于寻找知识之间的连接点，将碎片化的知识连成线、结成网、筑成块、构成体，让学生整体感悟学习内容、学习进程，帮助学生建构整体的结构思维，建构学生的思维体系和认知结构。也就是说教师要对离散的、断裂的、散点的知识点进行梳理和整合，从而使知识呈现整体结构和体系。从人教版的教材编排来看，“图形的面积”集中在三年级、五年级和六年级，虽然一二四年级没有面积知识内容，但是一年级的立体图形，二年级的平面图形和四年级的多边形的认识是“图形的面积”的相关知识的前沿知识，也是关联的知识，为“图形的面积”的学习奠定基础。另外，教材对“图形的面积”编排具有层次性，体现螺旋上升的认识策略。三年级下册“认识面积”“长方形和正方形的面积”知识，这是对“图形的面积”的后续教学铺下垫脚石；五年级上册学习“平行四边形的面积”“三角形的面积”“梯形的面积”“组合图形的面积”和“不规则图形的面积”的估算，这部分知识教材编排上相对集中学习多种图形的面积；五年级下册和六年级下册学习“立体图形的表面积”；六年级上册学习“圆的面积”，还有扇形，为今后学习扇形的面积奠定基础。教师在教学活动中必须具备整体相关知识的教学思维。在知识的大概念下，理解教材编写的逻辑、教材编排的内容、教材教育原理、教材的应用技术和创作空间的专业化能力。

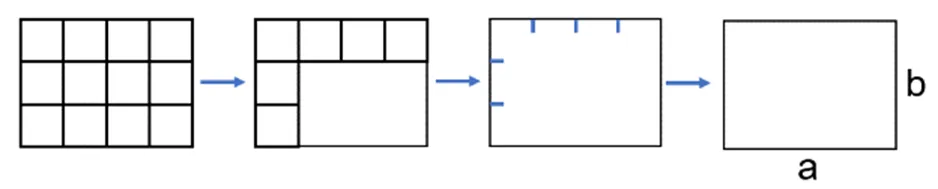
二是聚焦目标结构化。结构化学习应注重追求教学目标，无论是一课时还是单元的教学，都应以知识点的核心目标为中心，核心目标具有连续性和统领性。小学数学学习内容是整体性的，涉及小学数学知识核心要素的结构，这就引发学习目标的整体构建，包括对学习内容、学习原因、学习方式、学习程度的整体把握。比如教学三年级下册“长方形和正方形的面积”和五年级上册“多边形的面积”时，教师确定如何推导出各种图形的面积计算公式为每一课时的教学目标：长方形和正方形面积公式的推导、平行四行面积公式的推导、三角形面积公式的推导、梯形面积公式的推导。每一课时都隐含着对面积公式的推导过程。比如教学“长方形和正方形的面积”时，引导学生从面积单位的测量到长度单位的测量，从而推导了如下图的长方形面积计算公式。

三是聚焦方法结构化。小学数学结构化教学是以知识体系和学生的现有认知为基础，以整体结构为抓手，形成知识自主建设过程中的方法结构。方法结构的形成遵循学科整体结构的本质特征，遵循数学知识内在的逻辑机理，通过结构化、模块化重构、递进教学，逐步帮助学生建立清晰的知识结构，以及获取知识的方法结构。比如人教版三年级下册“长方形的面积”和五年级上册“多边形的面积”这个知识结构依次探究“长方形和正方形的面积”“平行四边形的面积”“三角形的面积”“梯形的面积”和“组合图形的面积”，每个课时的教学目标是公式的推导，但是每个课时的推导方法是不同的，每节课的立足点也是不同的。

“长方形的面积”的公式推导方法是替换，从面积单位的测量到长度单位测量的过程，用长度的计算替换面积单位的计算；“平行四边形面积”公式推导的立足点是长方形的面积，推导的方法是等积变形，通过剪、移、拼把平行四边形等积变形成长方形；“三角形面积”公式推导的立足点是平行四边形的面积公式，推导的方法是建立关系，把平行四边形切割成两个完全一样的三角形，建立三角形的面积等于平行四边形面积的一半的关系，再建立同底等高的三角形和平行四边形的面积关系；“梯形面积”公式推导的立足点是平行四边形的面积及三角形的面积，推导方法是工具的运用，会用学过的替换、等积变形和建立关系等多种方法进行推导。当学生有了这些方法结构，再研究组合图形、不规则图形和圆的面积时，学生可以自主运用类似的方法解决问题。这些方法结构一旦形成，就会有很强的迁移能力和运用能力，为他们未来探究未知的世界积累丰富的数学活动经验。

五、结语

概而言之，“四维度”教学法核心是通过课堂教学让学生深度建构数学知识，凸显小学数学课堂“转识成智”的价值意蕴，并着力培养创造性解决复杂问题的高阶思维能力，全面提升学生素养。

[1] 张敏.培养小学生高层次数学思维的研究[D].苏州:苏州大学,2020.

[2] 李素娜.立足数学本质,培养学生高阶思维能力[J].天津教育,2021(14):20-21.

[3] 陆晓明.高阶思维:学生数学思维培育的应然诉求[J].数学教学通讯,2021(19):21-22.

[4] 王小波.小学生数学高阶思维能力培养的教学探索——以基于学力单的“五环教学法”为例[J].教育科学论坛,2021(08):63-67.

G424

A

1002-7661(2022)22-0010-03