精细复合多尺度模糊熵在电机轴承损伤检测中的应用

苏晓燕，刘学申

（1.国家知识产权局专利局专利审查协作河南中心，河南 郑州 450046；2.郑州航空工业管理学院 航空宇航学院，河南 郑州 450046）

轴承作为电机的主要旋转部件，运行环境复杂且承受较大的负载，容易发生不同程度的损伤[1-2]，对传动系统的安全运行构成威胁. 因此，发展稳定可靠的轴承损伤识别方法极为重要. 电机轴承损伤检测常见的方法有基于图像的故障诊断方法[3]、基于模型的故障诊断[4]和基于声发射的故障诊断方法[5]. 目前，多数轴承损伤检测技术主要依托其振动信号. 随着非线性分析技术的发展，条件熵、样本熵和模糊熵等一系列复杂度度量方法也应用在电机轴承损伤检测中，如Chen等人[6]通过建立模糊函数替代固定容限，提出了模糊熵算法（Fuzzy Entropy，FuzEn）. 该方法模糊了向量间距的计算标准，有效克服了样本熵（Sample Entropy，SampEn）的不足，并在滚动轴承的特征提取中取得了良好效果[7-8]. 样本熵和模糊熵等方法在单一尺度下部分信息会被忽略，为此，Costa等人[9]提出了多尺度熵理论，郑近德[10]则把多尺度模糊熵（Multiscale Fuzzy Entropy，MFE）应用于轴承故障诊断. 但是，由于尺度因数的不断增加会导致原始信号长度急剧减小，从而使得熵值波动增大、误差增高，影响特征识别效果.

为此，本文提出精细复合多尺度模糊熵（Refined Composite Mutiscale Fuzzy Entropy，RCMFE）以克服传统算法的不足. 通过无限特征选择算法（Infinite Feature Selection，Inf-FS）[11-12]进行特征评估，构建诊断向量；最后，利用最小二乘支持向量机（Least Squares Support Vector Machine，LS-SVM）[13-14]完成分类，实现电机轴承的智能故障辨识.

1 理论背景

1.1 多尺度模糊熵

假定一组长度为N的振动信号：x j(j= 1,2,···,N)，通过模糊熵计算可得单一尺度的模糊熵值，为从多维时间尺度挖掘信号的动态特征，需对原始序列x j(j= 1,2,···,N)，进行粗粒化处理得新的时间序列，其计算原理可见图1，公式如下：

图1 粗粒化过程原理图

式（1）中，τ为尺度因数，表示小于b的最大整数. 之后，依次计算所有新序列的熵值可得多尺度模糊熵：

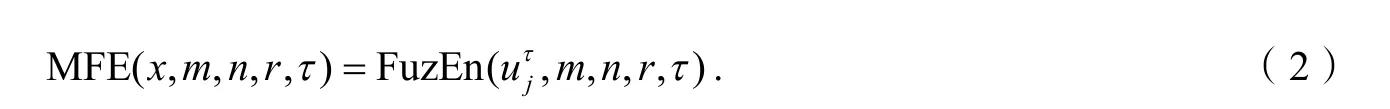
1.2 精细复合多尺度模糊熵

由前文分析可知，粗粒化程度的加深必然造成样本长度减少，从而导致熵值产生不规则波动，增加误差. 为克服这一缺点，本文将粗粒化过程进行优化（原理见图2），然后与模糊熵算法组合得到精细复合多尺度模糊熵，其具体计算步骤如下[15]：

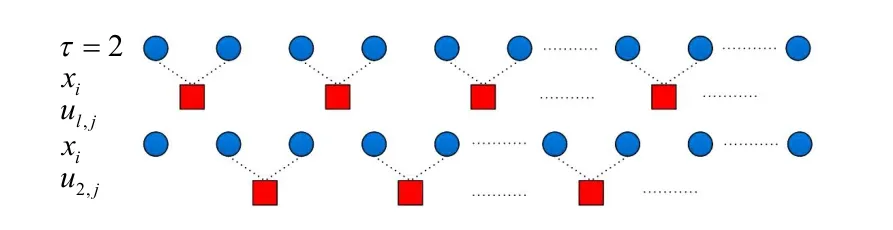
图2 改进粗粒化过程原理图

将粗粒化过程的首个点逐次位移，共位移τ-1次，使得同尺度下产生τ组粗粒化序列：

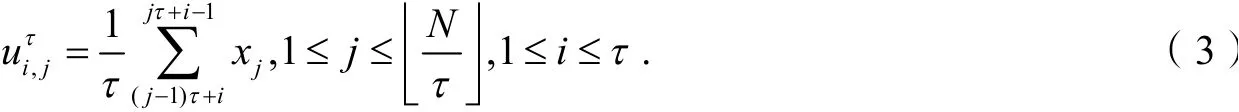
分别计算所对应的向量平均概率 ，则精细复合多尺度模糊熵可定义为：

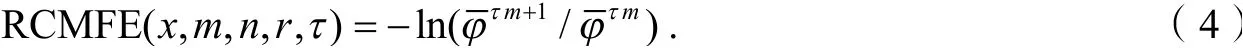
比较图1、2及算法原理可知，相较于MFE，RCMFE通过粗粒化首个点递推在同尺度下构建了多组新序列，使得粗粒化过程覆盖到每组相邻点，随后，每组粗粒化序列对应的条件概率相互补充特征信息，最终达到了校正误差和增强熵值一致性的目的.

2 对比分析

本节选用高斯白噪声（WGN）和粉噪声（1/fnoise）作为输入信号，分别计算不同数据长度下噪声信号的熵值，进而比较两类算法的具体性能.

参考文献[8]设定MFE、RCMFE的参数为：m=2，n=2，r= 0.15·SD，τ=20. 计算长度N= 512 ～ 8192信号的各50组熵值，求其均值和标准差，计算结果如图3所示. 由图可知，对于长度N=512的信号，MFE和RCMFE的熵值均表现出明显的波动，且随尺度因数增大误差递增. 之后，随着数据长度增加，15～20等大尺度下的熵值波动被有效抑制，直至N= 8192时，MFE和RCMFE才获得误差最小的熵值. 由此可知，两类算法的计算结果稳定性与数据长度成正比，样本量越大则相应熵值的鲁棒性越强. 而具体比较1/f噪声信号熵值可知，当N= 2 048时，MFE、RCMFE所得熵值曲线已趋于稳定，且随数据长度继续增加数据波动愈加微弱，整体稳定性有所提升但增幅较小，而过多信号样本将会极大增加计算负荷，因此，为平衡熵值鲁棒性与计算效率的关系，综合考量，选取N= 2 048作为MFE和RCMFE的标准数据，以完成后续实验.

对比图3和图4可知，对于相同长度的信号，RCMFE所得熵值无论其曲线平滑度还是分布一致性均优于MFE，该现象在N=512时尤为明显. 因此可得，对于短时间序列，RCMFE具有更好的自适应性，能有效克服传统算法对数据长度的依赖. 综上所述，数据长度对MFE的稳定性有显著影响，但RCMFE一定程度上削弱了该现象，使其整体稳定性强于MFE，性能更优.

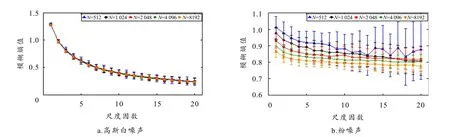
图3 不同数据长度下的MFE熵值图

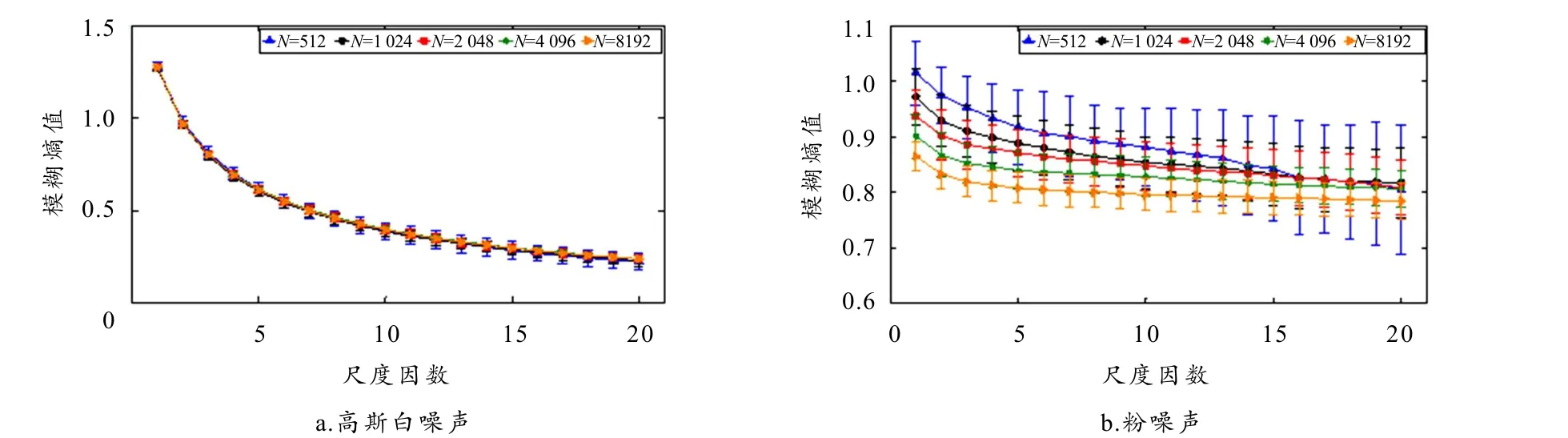
图4 不同数据长度下的RCMFE熵值图

3 实验验证

3.1 实验介绍

本节选用凯斯西储大学（Case Western Reserve University，CWRU）的轴承振动信号作为实验数据[16]，试验台示意图如图5所示，该实验平台主要由一台1.5 kW的异步电机、功率测试机、加速度传感器、转矩传感器/译码器组成，驱动端轴承型号为SKF6205，内圈直径25 mm；外圈直径52 mm；滚子直径8.18 mm. 其不同工况的损伤由电火花加工，状态数据可见表1，时域波形示于图6.

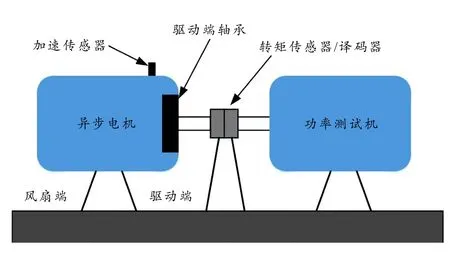
图5 轴承试验台

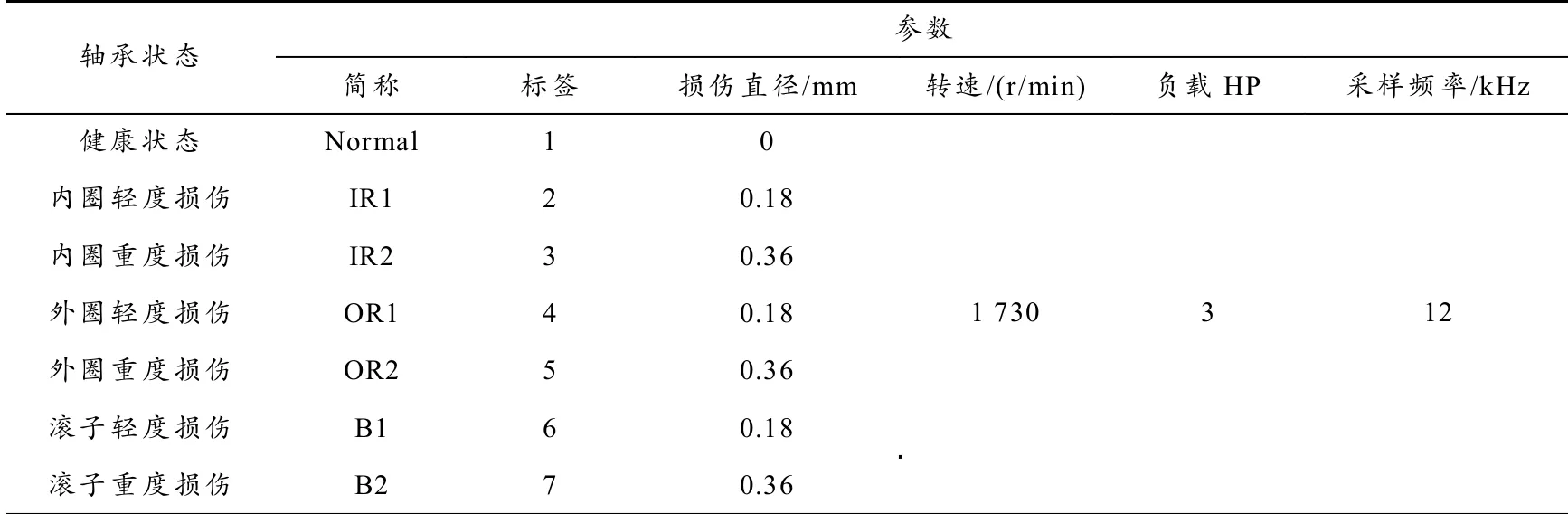
表1 轴承参数

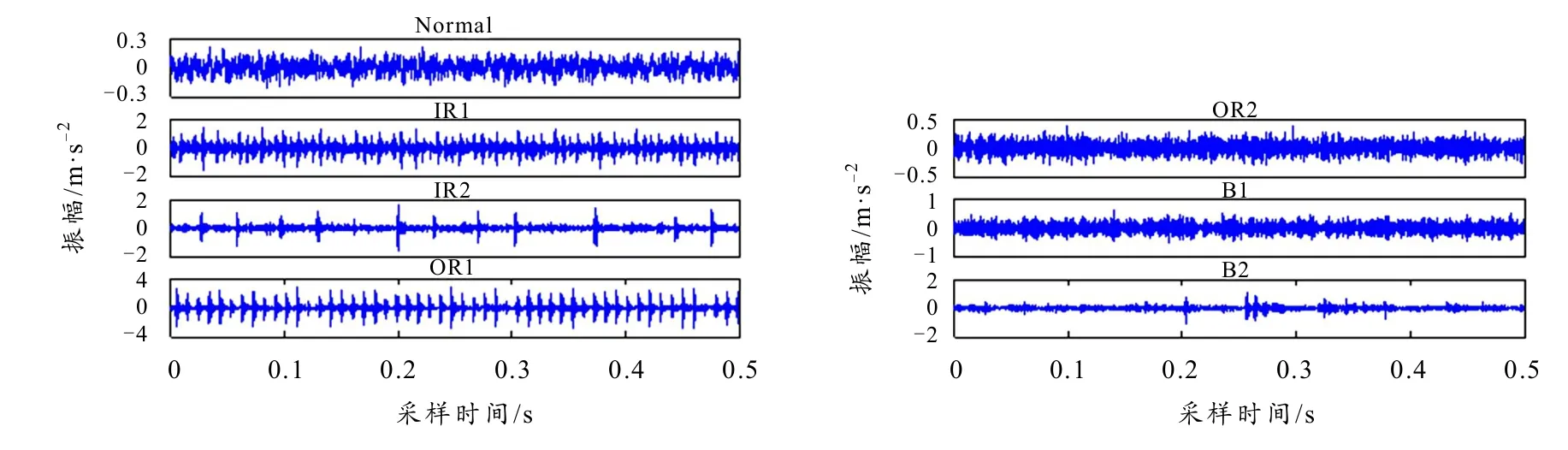
图6 不同运行工况下的轴承振动信号波形

3.2 特征提取

以第2节分析为基础，设定两类算法的参数为：m=2，n=2，r= 0.15·SD，τ=20. 分别采集N= 2 048的轴承信号各50组，并计算其熵值和误差，计算结果如图7所示. 由图可知，两类算法的熵值分布较为类似，其中，轴承健康状态的熵值在多数时间尺度下均大于其他故障状态. 结合图5可知，健康状态的振动信号具有明显的非稳定特征，因而其不规则度更高，所得熵值最大. 相较而言，OR1信号的振动规律呈周期性变化，故其熵值最小且远小于其他状态. 上述现象表明RCMFE、MFE所得熵值大小与时域波形的振动特性相契合，能够有效表征轴承的运行工况.

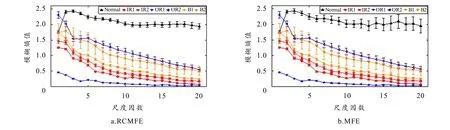
图7 轴承不同工况的RCMFE与MFE分布图

同时可知，相较于MFE，RCMFE有效抑制了熵值浮动，使得同类特征紧密分布，不同特征界限清晰. 该现象在轴承各类状态均有体现，而在健康状态最为明显. 充分证明对于实测信号，RCMFE亦展示出较强的性能优势，适用于轴承信号的特征提取.

4 结果分析与讨论

结合前文分析及图7可知，两类熵值在不同时间尺度下的分布情况各异，因此，仅靠单一尺度特征无法准确刻画轴承信号的动态变化. 为有效区别期间差异，本节选用Inf-FS算法评估不同尺度的熵值冗余性，冗余程度越高则证明轴承不同工况熵值分布越混乱，从而权重占比越低，以此为基础甄选最优尺度的特征构建诊断向量. 最后，利用LS-SVM完成特征分类，通过比较分类精度，进一步讨论RCMFE优势所在.

RCMFE与MFE的Inf-FS权重如图8所示，根据图中所得结果，分别挑选两类算法权重值最大的前5个尺度熵值构建诊断向量. 之后，随机抽取该向量中轴承每种状态10组数据共70×5组作为训练组，剩余40组数据共280×5组作为测试组，依次放入LS-SVM中进行训练和分类，并将该随机实验重复30次，所得结果如图9.

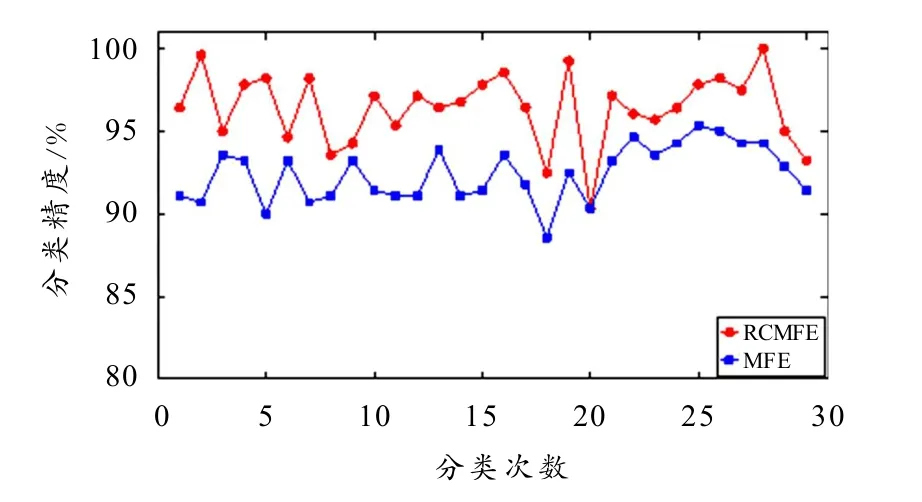
图9 随机实验分类精度

由图8可知，在30次实验中，RCMFE仅有第20次实验的分类精度与MFE相等，其余实验结果均大于MFE. 为了展现本算法的优越性，与多尺度样本熵（Multi-scale sample entropy，MSE）[17]、多尺度Lempel-Ziv（Multi-scale Lemple-Ziv，MLZ）[18]方法进行对比. MSE的参数设置为m=2，r= 0.15·SD，τ=5，MLZ参数设置为τ=5，特征分类设置与上述一致. 其分类精度见表2. 由表2可知RCMFE方法的均值高于MFE、MLZ、MSE. RCMFE的最大值、最小值和均值都比MFE多1%～5%，虽误差略高但整体精度更好，损伤识别结果更为可靠，印证了RCMFE的优化过程有效抑制了熵值波动，对诊断精度的提高起到了较为积极的影响.

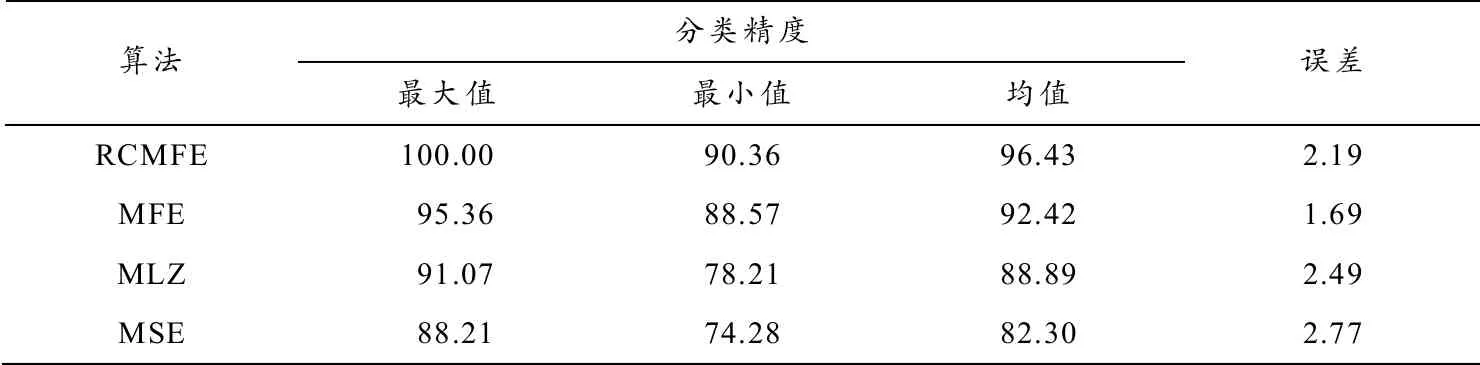
表2 随机实验统计数据 %

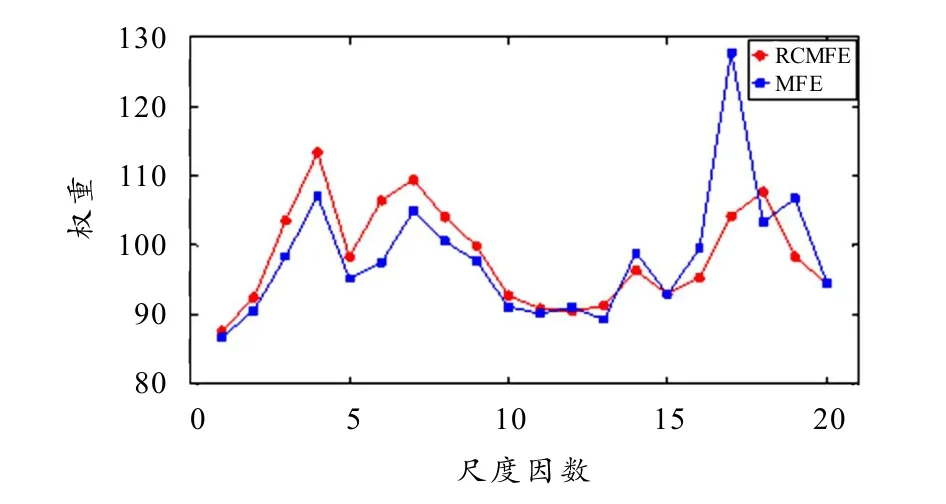
图8 Inf-FS特征评估结果

为获得详细损伤识别结果，依托上述条件完成第31次随机实验，分类结果如图10所示. 由图可知，RCMFE于IR2、B2发生了一定程度的误判，280组样本中共有6组未能正确分类，整体精度为97.86%. 反观MFE、MLZ、MSE，除健康状态和内圈轻度损伤被完整识别，轴承其余状态均出现误判样本，整体精度分别为92.50%、88.89%、82.30%. 对比可知，MFE、MLZ、MSE的误判范围及概率均大于RCMFE，与30次随机实验的结果具有较高的相似性，充分证明MFE、MLZ、MSE对关键特征的约束力小于RCMFE，致使诊断向量中各类特征的一致性较差，从而影响了特征识别效果.

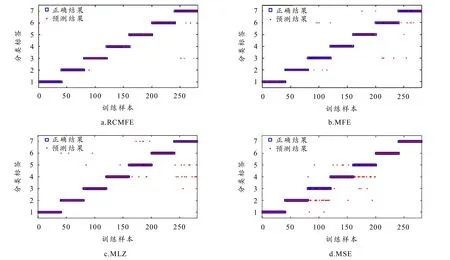
图10 4种算法的分类结果

5 结 论

通过对传统多尺度模糊熵的优化，提出了精细复合多尺度模糊熵算法，并将其应用于电机轴承的损伤检测中，通过实验分析可得出如下结论：

1）RCMFE能有效缓解粗粒化过程中的降采样现象，通过构建多组时间序列补充连续性特征信息，降低了MFE对数据长度的依赖性.

2）对于噪声信号和实测信号，同等条件下，RCMFE所得熵值相较于MFE误差更小、稳定性更强.

3）最后，利用CWRU轴承数据完成了实验验证，结果表明RCMFE取得了更高的诊断精度.

尽管该方法能有效表征轴承运行状态，但由于加入了模糊函数并计算了同尺度下多组粗粒化序列的条件概率，可能导致其计算耗时过高. 为此，笔者将继续深入研究，优化 RCMFE的特征提取效率，以满足对电机轴承状态实时监测的需求.