飞机液压裂纹管路动力学分析及其泄漏故障诊断
权凌霄,何顺君,温锐杰,魏坤池,郭长虹
(1.燕山大学机械工程学院,河北秦皇岛 066004;2.河北省重型机械流体动力传输与控制实验室,河北秦皇岛 066004)
0 前言
飞机液压管路系统具有“多散乱长杂”的特点。以C919飞机为例,全机液压管路共有1 186根,管路总长为884 m,而且其空间构型复杂,连接形式多样,管路系统遍布机身各个部位;此外,飞机液压管路系统在服役过程中承受五大适航载荷,包括介质压力、温度、机体变形、振动及加速度,而且在机身不同部位,这些载荷按照相应的规则相互叠加耦合。液压管路系统故障在飞机元件类故障中占比最高,是飞机故障的主要形式之一。循环压力冲击是液压管路系统泄漏的主要原因之一。当管路表面存在一定的缺陷时,循环压力会不断冲击缺陷,最终形成贯穿性裂纹,导致管路系统发生泄漏故障。据统计,设备外泄漏中管路的泄漏量占44.5%。
液压冲击会引起管路的流固耦合振动,进而降低系统元件的寿命,甚至造成管路系统结构破坏,导致事故发生。在研究裂纹管路动力学特性时,飞机液压管路流固耦合振动问题也不容忽视。
目前研究裂纹管路流固耦合振动的方法主要是通过牛顿法建立裂纹管路运动方程,并对其进行数值求解,分析管路动力学特。秦雷基于Euler-Bernoulli梁理论,在GREGORY和PAIDOUSSIS基础上,考虑航空发动机机匣激励,建立固支约束下管路运动方程,并通过数值方法进行求解,分析质量比、流体压力等对其固有频率的影响。杜林森、盛叶舟等基于Euler-Bernoulli梁理论,分别建立考虑航空发动机机匣激励的卡箍连接的双管耦合振动运动方程和Winkler地基约束裂纹管路的横向运动方程,并通过数值方法进行求解,分析质量比、流体压力、环向裂纹位置、裂纹深度等对管路固有频率的影响。包日东、梁峰基于GREGORY和PAIDOUSSIS推导的输流管路非线性运动方程,建立了自激励和外激励下一般支撑含圆周裂纹管路运动方程,采用Galerkin法进行求解,分析了裂纹位置、裂纹深度等对管路固有频率、失稳临界流速的影响。
本文作者建立两端固支约束的液压管路流固耦合振动方程,在无裂痕管路模态函数中加入三次多项式构造裂纹管路的模态函数,分析了裂纹圆周角、裂纹位置对管路动力学特性的影响;考虑在循环冲击作用下管路裂纹会扩展成贯穿性裂纹情况下,对循环压力冲击作用下飞机液压管路泄漏故障进行模拟,通过小波变换和负压波法检测及定位管路泄漏位置,最后开展管路泄漏实验,验证检测方法的精确性。
1 建立管路流固耦合振动方程
1.1 前提与假设
以两端固支约束直管路为研究对象,建立的管路模型如图1所示。
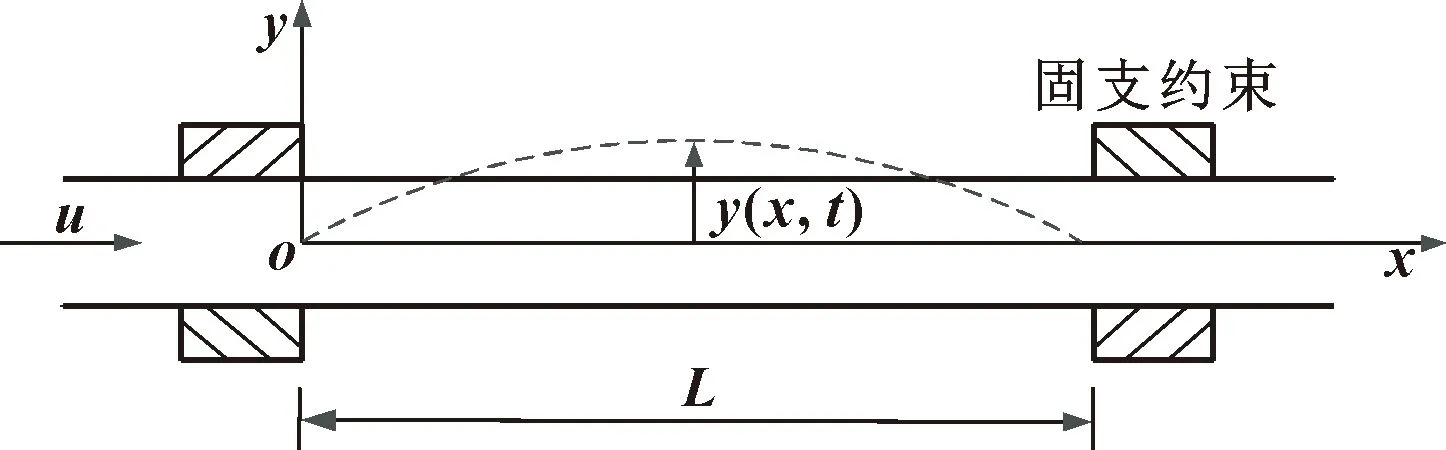
图1 两端固支约束管路模型
其中:为流体流速;为管路长度;(,)为时刻管路截面处距平衡位置的距离。建立飞机液压管路流固耦合振动方程需做以下假设:
(1)在低频振动时忽略剪切变形以及截面绕中性轴转动惯量的影响;
(2)管路在平面内作微幅弯曲振动;
(3)管路材料为Kelvin-Voigt黏弹性材料。
1.2 建立管路振动方程
如图2所示,对流体微元和管路微元进行受力分析。流体微元和管路微元长度均为δ。
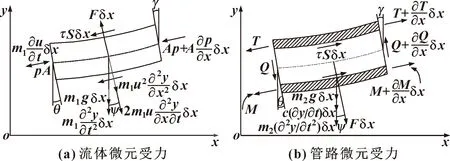
图2 流体与管路微元力学模型
其中:(,)为流体压力;为流体流过的面积;为管路截面所受弯矩;为流体单元垂直方向的压力;为管路中横向剪切应力;为流体流过的面周长;为纵向拉应力;为管路内表面的剪切应力;为流体微元的质量;为管路微元的质量;为管路的黏性阻尼系数;(∂∂)δ为离心惯性力; 2(∂∂∂)δ为科氏惯性力;(∂∂)δ为横向惯性力。为流体微元和管路微元的左端截面转角;为中间横向截面转角;为右端横向截面转角。本文作者仅考虑管路小变形下的情况,流体微元和管路微元截面转角很小,即=sin=tan=∂∂, cos≈1,=sin=tan=∂∂+(∂2∂)δ, cos≈1,=sin=tan=∂∂+(∂∂)δ, cos≈1。
流体微元在方向的平衡方程为

(1)
流体微元在方向的平衡方程为

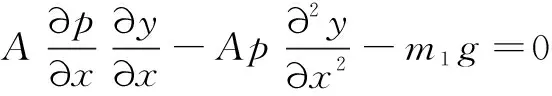
(2)
管路微元在方向的平衡方程为
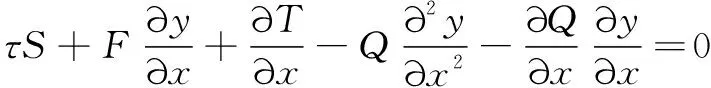
(3)
管路微元在方向的平衡方程为
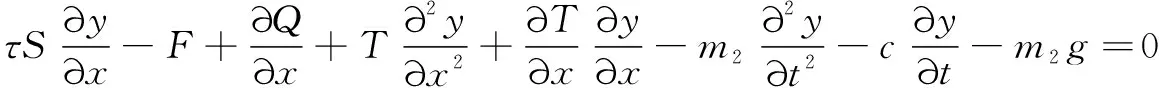
(4)
整理得
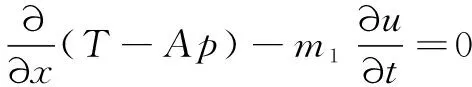
(5)
对上式在[,]上积分得

(6)

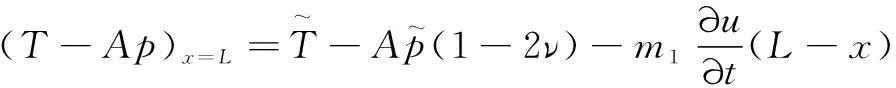
(7)
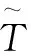


(8)
式(8)是完善后的输液管路流固耦合横向振动的线性方程。飞机液压管路材料多为合金材料,因此取=0。在小变形的条件下考虑定常流,即∂∂=0,忽略重力及管路外阻尼影响。则上述方程简化为
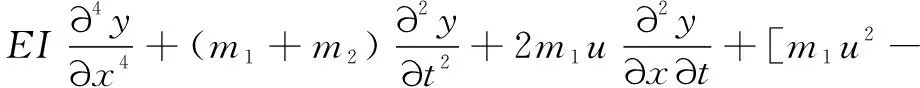
(9)


(10)
2 确定裂纹管路模态函数
2.1 固支约束无裂纹管路模态函数与频率方程
飞机的液压管路通常是通过卡箍将管路约束到飞机机体的机架上,所以将管路边界条件设置为两端固支。其表达式为
(0)=()=0,(0)′=()′=0
(11)
其中:为管路长度。令边界条件下的模态函数中值为1。
在Euler-Bernoulli梁理论的基础上建立两端固支约束的管路横向弯曲振动模态函数
()=sin+cos+sinh+cosh
(12)
其中:(=1,2,3,4)为未知量。将式(12)代入式(11)就可以解得。

(13)
式(13)是关于的线性方程组,当其系数行列式为零时,存在非零解。对行列式求解可以得到两端固支约束直管路的频率方程为
1-coscosh=0
(14)
求解可得管路前两阶特征值,分别为4.73和7.85。
两端固支约束下直管路模态函数为
()=cosh()-cos()+

(15)
其中:为管路特征值。不同的管路特征值对应不同的管路模态函数。
2.2 裂纹管路局部柔度系数
假设管路裂纹尖端的应力在弹性范围内,在单裂纹直管路上,将裂纹区域划分为无限的矩形区域(如图3),可认为各个微小裂纹矩形区域的应力强度因子与无限长裂纹矩形区域应力强度因子相等,通过计算可得到裂纹处的柔度系数。在纯弯矩的作用下,裂纹管路由外壁部分圆周裂纹带来的局部柔度系数为

图3 环向裂纹的管路模型

(16)
其中:=(1+)4;=(1-)2;′=(1-),为管路材料的弹性模量,为管路材料的泊松比;为管路外径;为管路内径;=。()的具体表达式为
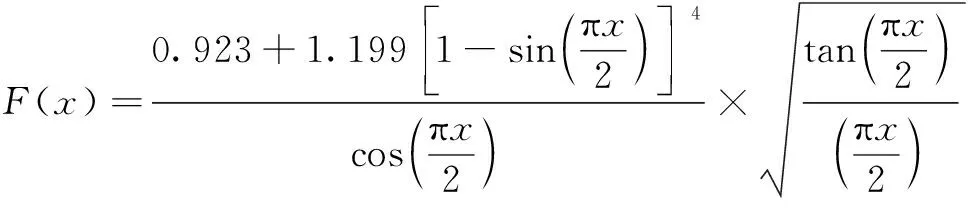
(17)
其中:为管路长度;为裂纹位置距管路左端距离;为裂纹深度;为管路壁厚;为管路外径;2为裂纹圆周角。
2.3 裂纹管路模态函数
对管路流固耦合振动方程进行求解时,需要确定裂纹管路的模态函数。一般是在无裂纹管路模态函数中加入3次多项式,构建裂纹管路的模态函数。根据无裂纹管路模态函数()推导得出裂纹管路的模态函数:
()=()++++(0≤≤)
(18)
()=()++++(≤≤)
(19)
其中:()为无裂纹管路模态函数;,,…,为未知量,且相应于各阶模态会有不同的值。
两端固支管路应满足固支约束的边界条件。此外,在裂纹位置处,还应同时满足横向位移连续性条件、弯矩连续性条件、剪力连续性条件和斜率条件。
横向位移连续性条件为
()=()
(20)
弯矩连续性条件为

(21)
剪力连续性条件为
‴()=‴()
(22)
斜率条件为

(23)
其中:为管路材料的弹性模量;为管路截面模量;为管路外壁圆周裂纹的局部柔度系数。
根据4个固支约束的边界条件、3个连续性条件和1个斜率条件联立方程求解式(18)和式(19)中的8个未知量(,,…,)。

(24)
求解式(24)方程组可以确定未知数。将结果代入式(18)和式(19),可得裂纹管路模态函数()和()。
2.4 裂纹管路振动方程离散化
采用Galerkin法对式(10)进行离散,无量纲的模态函数为

(25)
将式(25)代入式(10),整理得

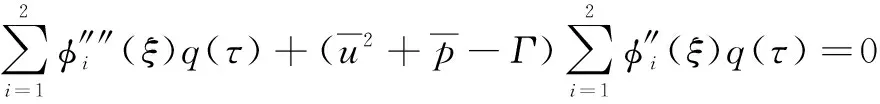
(26)
式(26)两边同时乘以()(=1,2),对其在区间(0,1)上进行积分,整理得

(27)
其中,矩阵、和的表达式分别为

(28)

(29)

(30)
式(27)和式(28)中矩阵、和的表示式分别为


(31)


(32)
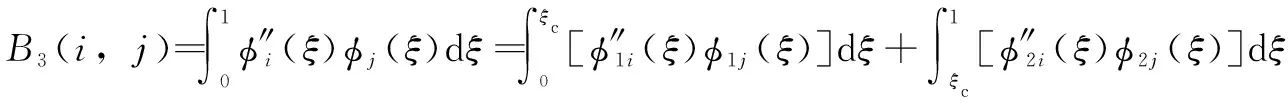
(33)
将式(27)进一步简化为

(34)
其中,矩阵和分别表示为
=-,=-
(35)
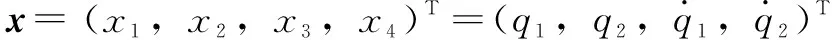
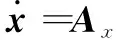
(36)
其中,矩阵的表达式为

(37)
矩阵的特征方程为
++++=0
(38)
2.5 裂纹管路固有频率分析
管路的无量纲固有频率和衰减系数分别表现在特征方程(38)求解结果的虚部和实部。
定常流会使两端固支的管路出现静力屈服,管路发生发散失稳(静态失稳)现象。当矩阵的特征方程(38)中为零时,特征方程的解会出现为零的特征值,管路发生发散失稳现象,此时管路中定常流的流速为静态失稳临界流速。在上述约束条件和定常流激励下管路的静态失稳现象可用一阶微分方程进行解释。设线性齐次方程为

(39)
式(39)解的形式表示为

(40)
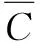
管路的状体与式(40)中的解有关,设其为实数,当>0时,随着的不断变大趋于无穷,此时式(40)的解失稳;当<0,随着的不断变大逐渐趋于0,此时式(40)的解稳定;当=0时,是失稳的临界值,这种条件下的失稳属于发散失稳。
裂纹位置、裂纹圆周角、流体流速、流体压力和质量比等参数均影响特征方程(38)的解。为探究上述参数对裂纹管路动力学特性的影响规律,给出液压管路工作参数如表1所示,并选取仿真参数。
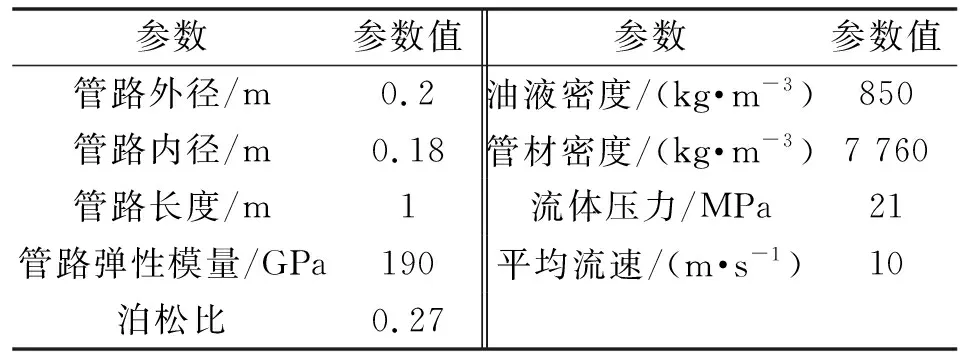
表1 管路工作参数

以裂纹相对位置为变量,对式(38)进行求解,得到管路固有频率随裂纹相对位置的变化曲线,如图4所示。
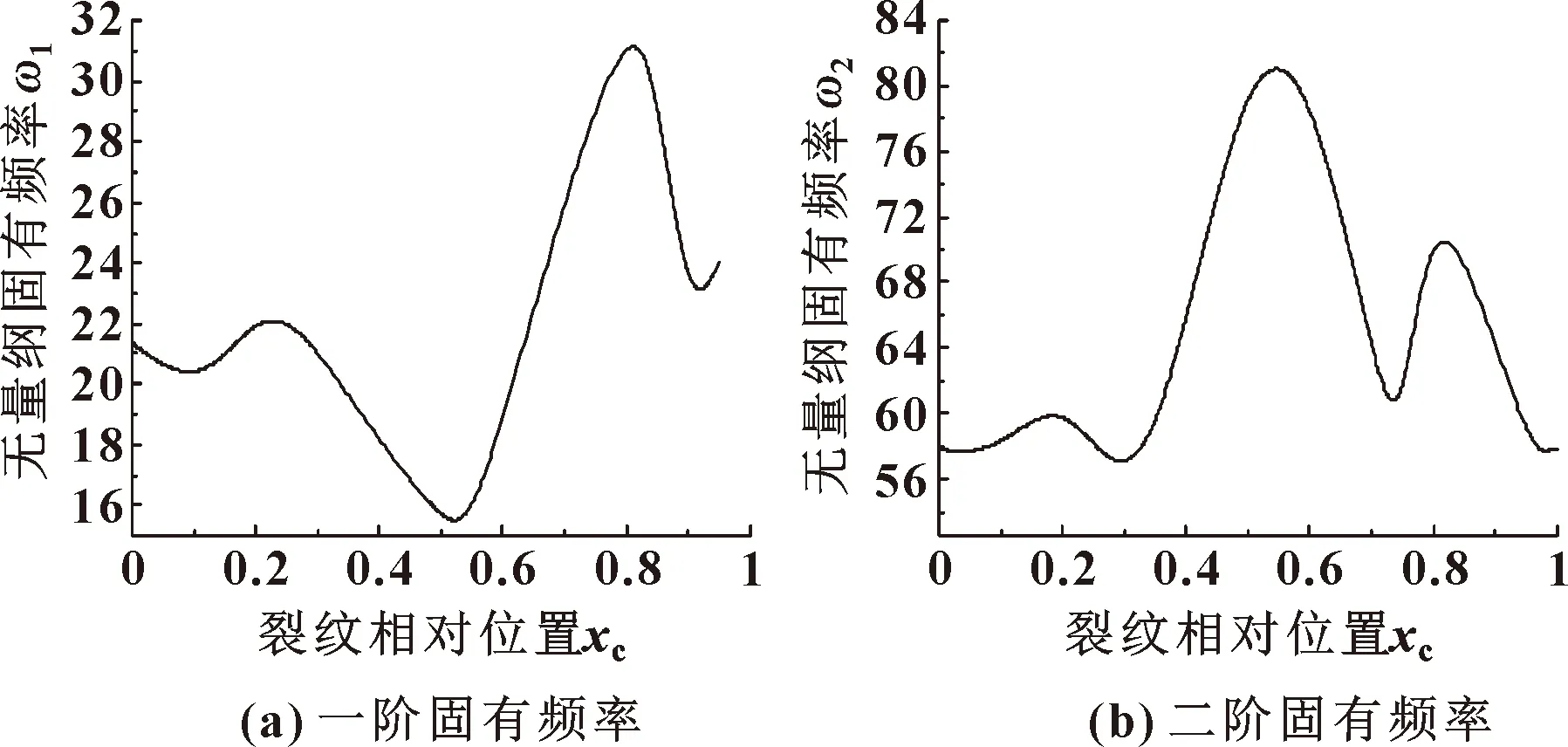
图4 管路固有频率随裂纹相对位置的变化曲线
分析图4中管路的前两阶固有频率随裂纹相对位置的变化趋势可以得出:当裂纹相对位置为0.5和0.8左右时,管路一阶固有频率和二阶固有频率均有极值。
将裂纹圆周角作为变量,对式(38)求解,得到管路固有频率随裂纹圆周角的变化曲线,如图5所示。

图5 管路固有频率随裂纹圆周角的变化曲线
分析图5两条曲线可以得出:管路前两阶固有频率随裂纹圆周角加大在较小范围内呈不同变化趋势,管路一阶固有频率随裂纹圆周角加大而逐渐减小,并最后趋于稳定;管路二阶固有频率随裂纹圆周角加大而逐渐增大,并最后趋于稳定;随着裂纹圆周角的增大,管路一阶固有频率逐渐下降,而二阶固有频率逐渐上升。
综上所述:裂纹位置和裂纹圆周角的变化均会影响管路的固有频率,管路固有频率受裂纹位置的影响更为明显。
2.6 裂纹管路静态失稳临界流速分析
通过控制变量法分析不同裂纹深度下裂纹位置和裂纹圆周角对管路静态失稳临界流速的变化规律。
对式(38)进行求解,得到不同裂纹深度下管路静态失稳临界流速随裂纹相对位置的变化曲线,如图6所示。
分析图6可发现:不同裂纹深度下管路的静态失稳流速随裂纹相对位置均出现先增大后减小的变化趋势,且变化剧烈程度随着裂纹相对深度的加大而增加。
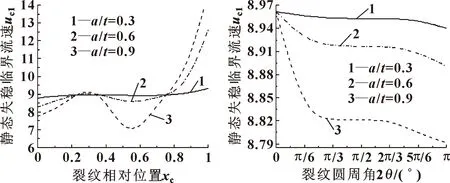
图6 管路静态失稳临界流速随裂纹位置的变化曲线
以裂纹圆周角和裂纹相对深度为变量,对式(38)进行求解,得到不同裂纹深度下管路静态失稳临界流速随裂纹圆周角的变化曲线,如图7所示。
分析图7可发现:不同裂纹深度管路的静态失稳临界流速随裂纹圆周角的加大而减小,当裂纹圆周角在[0,π/3]及[2π/3,π]区间内时,静态失稳流速随裂纹圆周角增加而显著减小;在[π/3,2π/3]区间时,静态失稳流速几乎不随裂纹圆周角增加而变化;在裂纹圆周角相同时,管路静态失稳临界流速的变化幅值随裂纹相对深度的加大而增加。
综上所述:裂纹位置、裂纹深度和裂纹圆周角的变化均会引起管路静态失稳临界流速的变化,裂纹位置的变化会对管路静态失稳临界流速产生较大影响。
3 循环压力冲击作用下管路泄漏故障分析
加工制造及现场装配会导致飞机液压管路外表面产生微缺陷,管路中的流体介质以循环压力冲击的形式作用到管路内壁,会导致缺陷逐渐加深加大甚至贯穿管壁,进而使管路系统发生泄漏。管路泄漏位置通过负压波法检测。
3.1 循环压力冲击作用下管路泄漏故障仿真分析
以正弦压力波模拟管路中的循环压力冲击,在AMESim中对不同泄漏情况下的管路故障进行分析。
仿真参数设置:时长10 s,步长0.001 s,泄漏位置距管左右两侧压力传感器分别为1.76 m和1.3 m,以节流阀模拟裂纹,节流阀在6.5 s受到阶跃信号控制。其开口直径为1、1.5 mm时,管路中压力曲线如图8所示。

图8 不同泄漏情况下管路压力曲线
分析压力曲线发现,管路在出现泄漏时,压力信号会表现出奇异性。选择合适小波函数对信号奇异性进行检测,通过对比得到,节流阀开口直径为1.5 mm时,采用db5小波函数检测压力曲线中的奇异性效果最好,可以清楚地看出奇异点的位置,其幅值较大而且很窄,如图9所示。
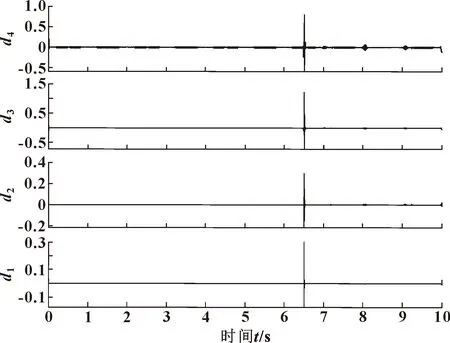
图9 压力曲线经db5小波函数分解细节
利用MATLAB对分解细节进行处理,确定各层细节信号的模极大值点,模极大值坐标信息如图10所示。
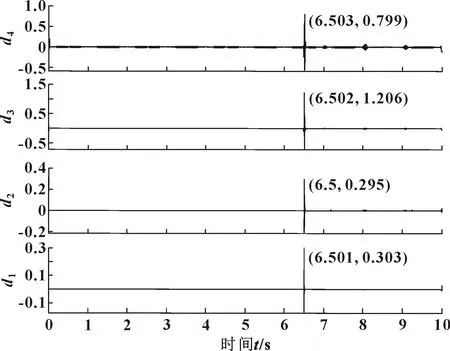
图10 模极大值点坐标信息
根据细节信号的4个模极大值点进一步计算可确定压力信号中奇异点发生时间在6.501 5 s。发现小波函数可精准检测泄漏情况下管路中压力曲线的奇异性,并能精准定位信号奇异点的位置。
3.2 循环压力冲击作用下管路泄漏故障实验研究
管路、截止阀以及压力变送器等在试验台上的安装方式如图11所示。
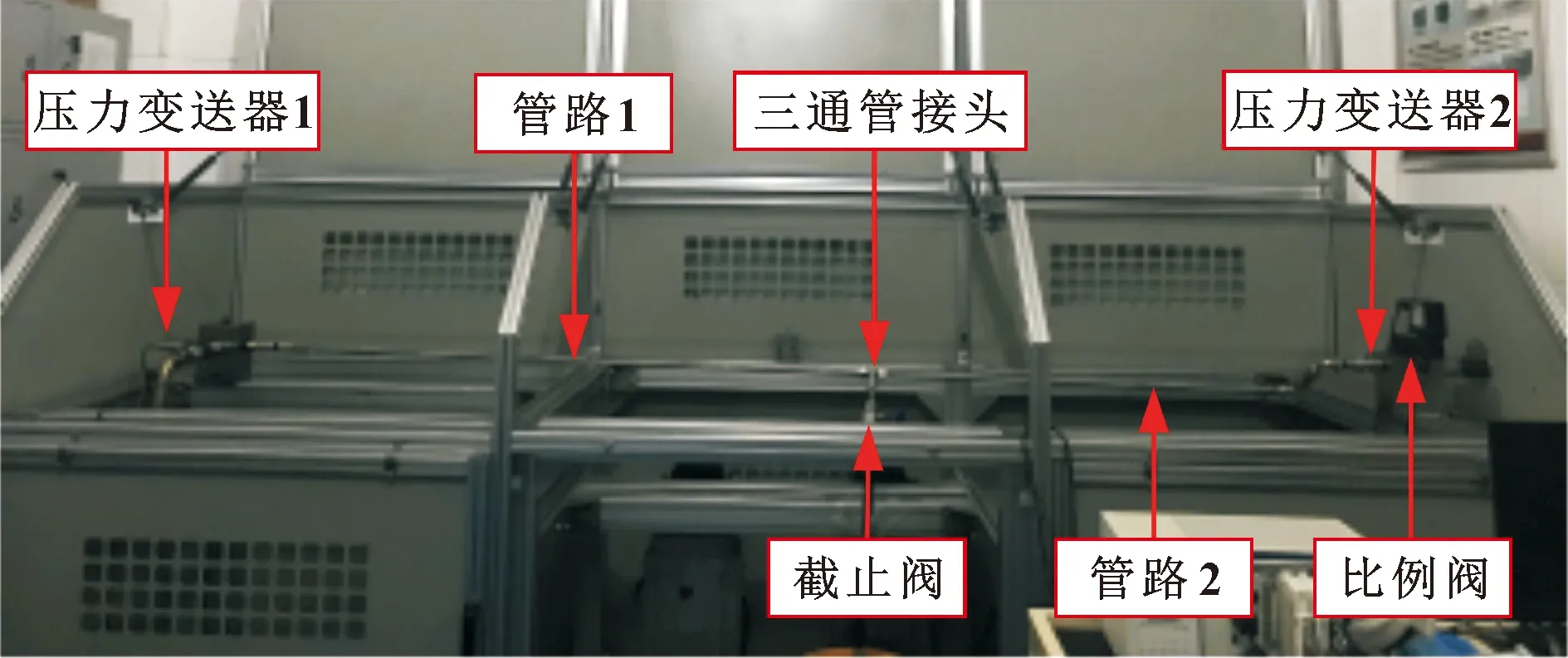
图11 实验管路及压力变送器安装
3.3 管路泄漏实验结果分析
输入信号为最大压力3.5 MPa、最小压力0.5 MPa、波形频率为0.5 Hz的正弦波,采样时间为10 s,采样频率为1 000 Hz。将压力变送器检测到的信号通过软阈值算法进行降噪处理,经降噪处理后的压力变送器1的压力曲线1如图12所示。
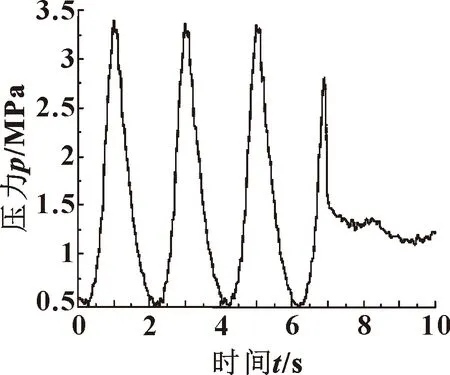
图12 压力曲线1
通过图12可以看出,第7 s时曲线会出现较大的奇异性。以db5小波函数对压力曲线进行分解,计算负压波从泄漏位置传播到压力变送器1的时间,分解结果如图13所示。

图13 压力曲线1 db5经小波函数分解细节图
分解细节图中的模极大值点坐标信息如图14所示。
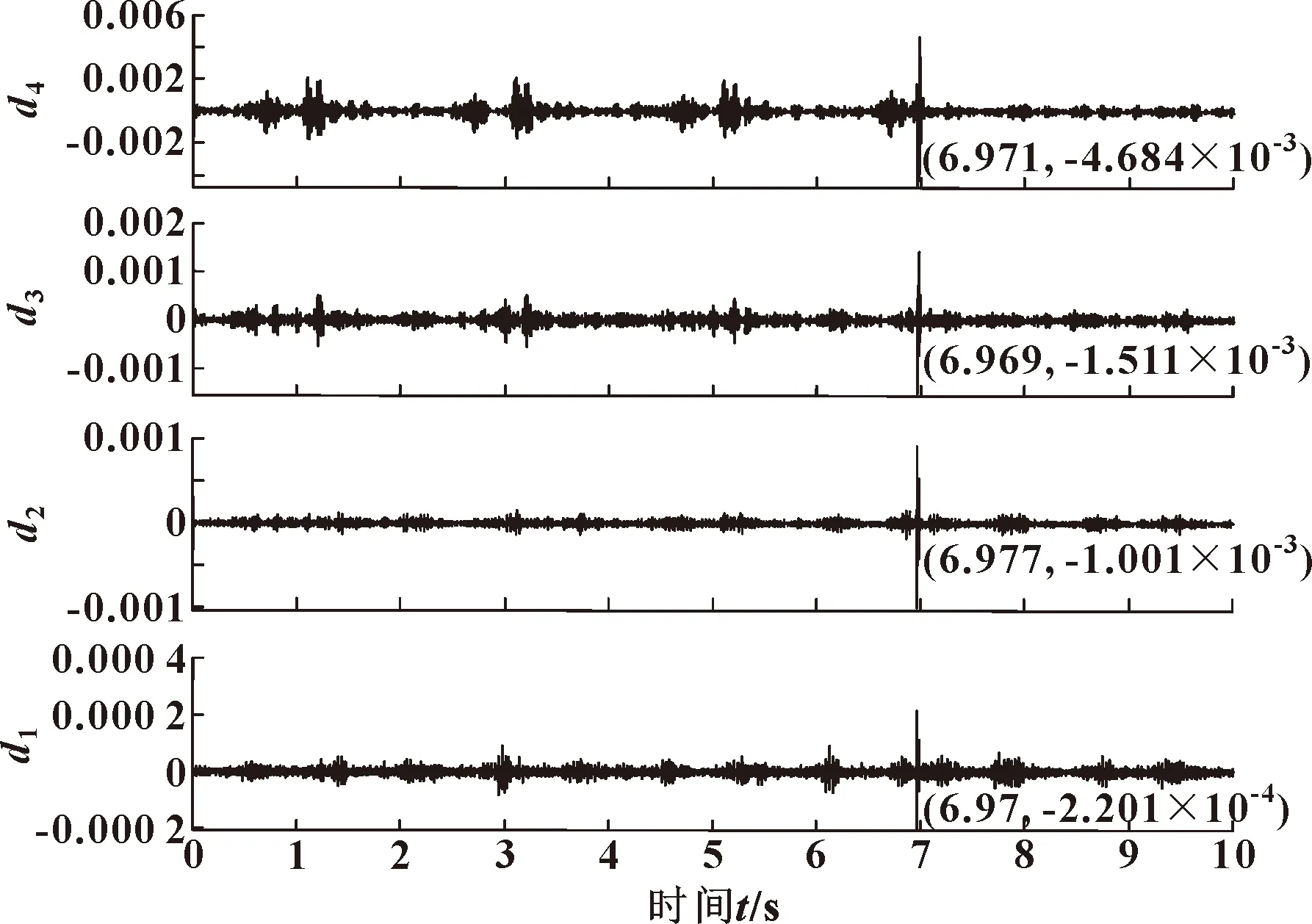
图14 模极大值点坐标信息
计算得到负压波从泄漏位置传播到压力变送器1的时间为6.971 75 s。
经降噪处理后的压力变送器2的压力曲线2如图15所示。

图15 压力曲线2
选取db5小波函数对压力曲线2进行小波分解,如图16所示。

图16 压力曲线2经db5小波函数分解细节图
计算得到负压波从泄漏位置传播到压力变送器2的时间为6.971 s。
两压力变送器间距为3.06 m,二者检测到的负压波信号时间差为0.000 75 s,负压波速1 073.8 m/s,根据负压波定位公式计算得泄漏位置距压力变送器1的距离为1.9 m,对比实际距离1.76 m,定位误差约为8%。
4 结论
通过建立飞机液压管路流固耦合振动方程以及两端固支约束裂纹管路模态函数方程,研究裂纹位置、裂纹圆周角对管路动力学特性影响规律;最后,考虑在循环冲击作用下管路裂纹会扩展成贯穿性裂纹情况下,对循环压力冲击作用下飞机液压管路泄漏故障进行模拟,通过小波变换和负压波法检测及定位管路泄漏位置,并开展管路泄漏故障实验,验证了检测方法的精确性。结论如下:
(1)裂纹位置和裂纹圆周角的变化均会影响管路的固有频率和静态失稳流速,且裂纹位置变化对二者的影响更为明显。
(2)管路裂纹的开口越大,发生泄漏故障时,管路中压力信号的奇异性越显著,利用负压波法可以精准检测泄漏发生位置。

