风机齿轮箱轴承应力及疲劳寿命分析
白浩宇, 穆塔里夫·阿赫迈德,2,白云松,鞠增鑫
(1.新疆大学机械工程学院,新疆乌鲁木齐 830047;2.新疆大学电气工程学院,新疆乌鲁木齐 830047)
0 前言
在风力发电机组中,增速齿轮箱是重要的部件之一,其运行状况的好坏与风力发电机运转密切相关。由于齿轮箱的工作环境十分恶劣,导致齿轮箱中输出轴端轴承受到复杂的载荷及剧烈的振动。根据数据统计,风电机组故障中齿轮箱失效占12%,而其中约50%为滚动轴承失效。由于密封差、润滑不足及变载荷,齿轮箱中滚动轴承各部件会出现疲劳点蚀、剥落等故障。因此,研究具有一定缺陷故障轴承的应力与疲劳寿命,对滚动轴承稳定运行和故障检测具有重要意义。
针对局部剥落缺陷轴承的动力学研究,国内外学者都进行了大量的相关工作。LIU等总结出一种改进的角接触球轴承动力学模型,研究了速度、负载和缺陷尺寸对角接触球轴承声学特性的影响。SINGH等采用显式动力学软件LS-DYNA对具有局部外滚道线剥落的滚动轴承的振动响应进行了数值模拟,并验证了轴承显式有限元模拟结果的正确性。剡昌锋等在考虑弹流润滑和滑动作用的前提下,建立有局部故障的轴承系统模型,进行动力学数值分析,并通过试验与仿真结果进行对比。张慧玲和吕福玲对带有点蚀缺陷的轴承的振动信号进行了数值模拟,并分析了其缺陷特征。涂文兵等建立了缺陷存在于轴承各部件上的数值模型,分析获得了滚子与其他部件的接触应力变化曲线,总结出缺陷对轴承各部件之间接触规律的影响。
研究者们通过仿真及试验对轴承疲劳寿命进行研究及预测。HE等在ABAQUS中建立了回转轴承的有限元模型,得到了球与滚道之间的接触应力,联合轴承数值分析结果和FE-SAFE计算了疲劳寿命和损伤。ZHANG等提出了一种准动态动力学模型来研究角接触球轴承在任意预紧力作用下的载荷分布,在此基础上,计算了该轴承在运转状态下的疲劳寿命。赵斗生等建立关于柔性轴承及波发生器多体动力学的接触模型,在数值分析出模型应力及变形的基础上,用nCode-DesignLife分析其寿命。耿民等人基于高速列车中牵引电机的轴承实际工况,用ANSYS建立了轴承的接触模型,考虑轴承各部件之间游隙变化引起的受载变化和应力集中,并提出了新的计算轴承寿命的方法。
本文作者以5 MW风力发电机齿轮箱输出轴端的轴承为研究对象,建立无缺陷轴承和不同尺寸局部剥落缺陷的轴承数值模型。利用显式动力学分析滚子进入外圈缺陷和退出外圈缺陷的应力变化;将各轴承应力结果导入疲劳软件进行寿命计算,从而得出局部剥落缺陷尺寸扩展对轴承应力和疲劳寿命的影响规律。
1 轴承模型及边界条件
1.1 几何与数值建模
选为圆柱滚子轴承(NU2232E),其几何参数如表1所示。针对风机齿轮箱轴承的实际工况,对轴承模型进行一些简化:不考虑轴承内圈、外圈的倒角,可以避免对轴承应力分布的影响;不考虑轴承径向和轴向的游隙。
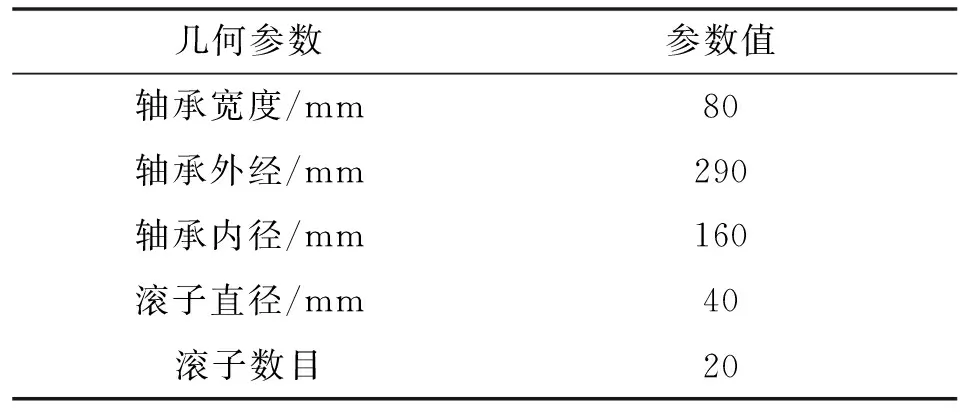
表1 NU2232E轴承参数
对模型进行有限元分析,先进行网格划分,文中应用HyperMesh对圆柱滚子轴承进行网格划分。轴承各部件均采用六面体网格,共计77 760个单元,如图1所示。轴承各部件材料均采用轴承钢,其材料参数:密度为7 820 kg/m,弹性模量为2.16×10MPa,抗拉强度为1 813 MPa,屈服强度为1 323 MPa。

图1 NU2232E轴承数值模型
1.2 边界条件
依据5 MW风机齿轮箱输出轴端轴承的实际工况,限制外圈、、方向的移动和旋转自由度,限制内圈方向的移动自由度和、方向的旋转自由度。对内圈施加50 kN的径向载荷和5种转速(800、1 200、1 600、1 800、2 000 r/min)。滚子与内圈、外圈采用面与面接触;不考虑保持架对轴承滚子的影响,将保持架设为刚体。为使轴承在开始时能够稳定运转,径向载荷先作用,0.01 s后转速和载荷同时作用,0.2 s时结束运转。
2 轴承数值分析
2.1 局部缺陷建模
在实际中,轴承外圈局部剥落缺陷的形状不规则,为方便划分网格进行仿真,将外圈缺陷理想化为矩形,轴承未运转之前,缺陷位于外圈上19号滚子与20号滚子之间,如图2所示。
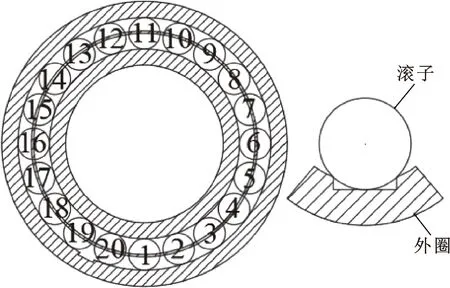
图2 滚子与外圈局部剥落缺陷示意
矩形缺陷长度40 mm,深度0.3 mm,选取不同宽度尺寸1、3、4、6和7 mm,模拟缺陷扩展对轴承各部件动力性能的影响。
2.2 应力分析
有局部剥落缺陷(宽度、深度分别为7、0.3 mm)的轴承运转过程中,滚子滚入外圈的缺陷和滚出外圈缺陷。选取无缺陷轴承和有缺陷轴承的1号滚子上与外圈接触面中间的节点,提取节点应力曲线,进行应力分析。
在转速800 r/min的情况下,轴承内圈受到径向载荷和转速的作用,有缺陷轴承和无缺陷轴承在0.12 s时的等效应力如图3所示,其各部件最大等效应力如表2所示。在整个轴承运转过程中,径向载荷和转速都是平滑加载,随着径向载荷和转速随时间不断加大,有缺陷轴承的等效应力大于无缺陷轴承的等效应力,这是因为缺陷轴承在运转到0.12 s时,滚子还未滚入缺陷,距离缺陷的边缘较近。提取两轴承1号滚子节点的等效应力曲线,如图4所示。可以看出:运转到0.12 s时,缺陷轴承滚子节点应力波动较大,这是由于其他滚子经过缺陷造成内圈受力偏载过大,1号滚子与内圈接触发生偏移,从而使得有缺陷轴承滚子节点应力大于无缺陷轴承节点应力。

图3 0.12 s时各轴承的等效应力云图

表2 轴承各部件在0.12 s时最大等效应力 单位:MPa

图4 滚子节点在0.11~0.12 s时等效应力
图5所示为有缺陷轴承和无缺陷轴承在0.13 s时的等效应力云图。可以看出:等效应力较大的是有缺陷的轴承。这是由于有缺陷轴承运转到0.13 s时,1号滚子准备滚入缺陷,与缺陷边缘接触,缺陷左边缘出现应力集中(如图6(a)所示),0.14 s时滚子滚出缺陷,与缺陷右边缘接触,右边缘出现应力集中(如图6(b)所示),使得载荷力无法作用在该滚子上,所以造成局部剥落缺陷轴承应力大的原因是缺少1号滚子来承受径向载荷的作用,使得内圈受力不均。图7所示为两轴承的1号滚子节点等效应力曲线,可以看出1号滚子滚入和退出缺陷的应力变化过程,3次应力幅值波动分别对应滚入缺陷、在缺陷里和滚出缺陷这3个事件。

图5 0.13 s时各轴承的等效应力云图

图6 缺陷边缘等效应力云图

图7 滚子节点在0.13~0.14 s时等效应力
不同转速下无缺陷轴承和有缺陷轴承各部件的最大等效应力分别如图8—图10所示。可知:径向载荷相同时,转速越大,轴承各部件的等效应力越大,其中内圈应力变化趋势最大,其次是滚子、外圈。随着缺陷尺寸的扩大,外圈的应力也逐渐增大。在实际中,齿轮箱输出轴端受到径向载荷的作用传递给轴承内圈,由于外圈存在局部剥落缺陷,每个滚子在滚入和滚出缺陷时,使内圈出现偏载过大,造成内圈应力集中。
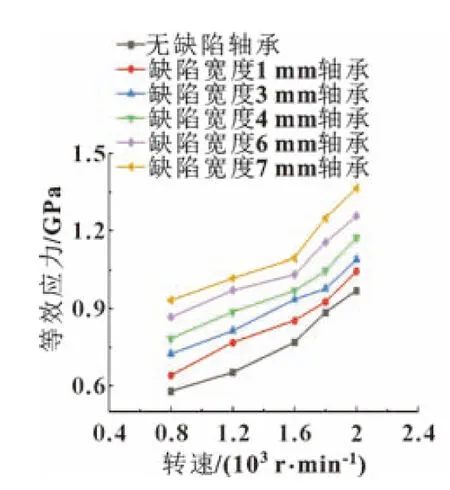
图8 各轴承内圈最大等效应力

图9 各轴承滚子最大等效应力

图10 各轴承外圈最大等效应力
3 疲劳寿命分析
3.1 疲劳损伤机制
疲劳损坏是指零件在运行过程中受到载荷的冲击从而发生损坏。在循环载荷施加于零件的作用过程中,零件上会产生应力集中区域,还会引起局部变形,从而使零件永久性损坏。另外,机构的运转使循环次数逐渐上升,机构发生故障的可能性也会增加。当循环次数到了一定数值后,该机构就不能工作了,也就是失效。
3.2 疲劳损伤理论
为更加准确地分析风机齿轮箱输出轴端轴承疲劳寿命,选用Palmgren-Miner累积损伤准则进行计算。在实际工况中,由于循环载荷对零件整体起作用,会引起零件材料损伤,而损伤的累积最终会使零件发生疲劳破坏。此理论中,损伤的大小与载荷的循环作用次数呈线性关系,而且零件失效时吸收的净功和负载历程都与零件的损伤无关。因此,可以推导出零件长期运转后发生疲劳失效时的应力循环次数和吸收的净功的关系为
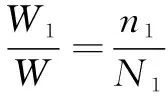
(1)
零件因次循环载荷作用产生各种应力,进而引起损伤,即:

(2)
式中:为零件在级别应力循环加载的次数;为零件在级别循环负载引起疲劳失效时的次数。因循环负载的冲击导致零件损伤大于等于1时(≥1),认为该零件已被破坏。
3.3 结果分析
前人通过试验总结出轴承疲劳寿命计算方法,分别是应变疲劳(E-N)和应力疲劳(S-N)。根据风电齿轮箱输出轴端轴承实际运转工况,轴承的运转属于高循环疲劳,所以采用名义应力法计算轴承疲劳寿命。仿真得到无缺陷轴承和局部剥落缺陷(宽度、深度分别为7、0.3 mm)轴承在转速为800 r/min时的疲劳寿命和损伤云图。
3.3.1 内圈疲劳分析
无缺陷轴承和有缺陷轴承内圈的疲劳寿命和损伤云图分别如图11、图12所示。

图11 内圈损伤云图

图12 内圈疲劳寿命云图
由图11、图12可知:无缺陷轴承内圈在节点N1764435处发生损伤,其最大损伤为2.240 86×10,在该节点处最小寿命为4.463×10次,而多数损伤在4.280×10~1.832×10,与之对应的疲劳寿命为2.336×10~5.460×10次;有缺陷轴承内圈在节点N1756404处发生损伤,其最大损伤为5.376×10,在该节点处最小疲劳寿命为1.860×10次,而多数损伤在3.107×10~4.087×10,与之对应的疲劳寿命为3.219×10~2.447×10次。轴承内圈内表面处发生损伤,从而可以获知该区域会出现故障,因为内圈受到径向载荷的作用,会出现应力集中,这与轴承动力学仿真结果内圈出现应力集中相符合。
由图11、图12还可以看出:在载荷和转速的作用下,有缺陷轴承内圈的最大损伤比无缺陷轴承内圈的最大损伤大,而且有缺陷轴承内圈的疲劳寿命比无缺陷轴承的疲劳寿命小。这是由于缺陷轴承运转时,滚子滚入和滚出外圈缺陷时,轴承内圈会出现偏载受力过大,造成内圈应力集中,导致发生损伤。
3.3.2 圆柱滚子疲劳分析
图13、14所示分别为无缺陷轴承和有缺陷轴承圆柱滚子的损伤和疲劳寿命云图。
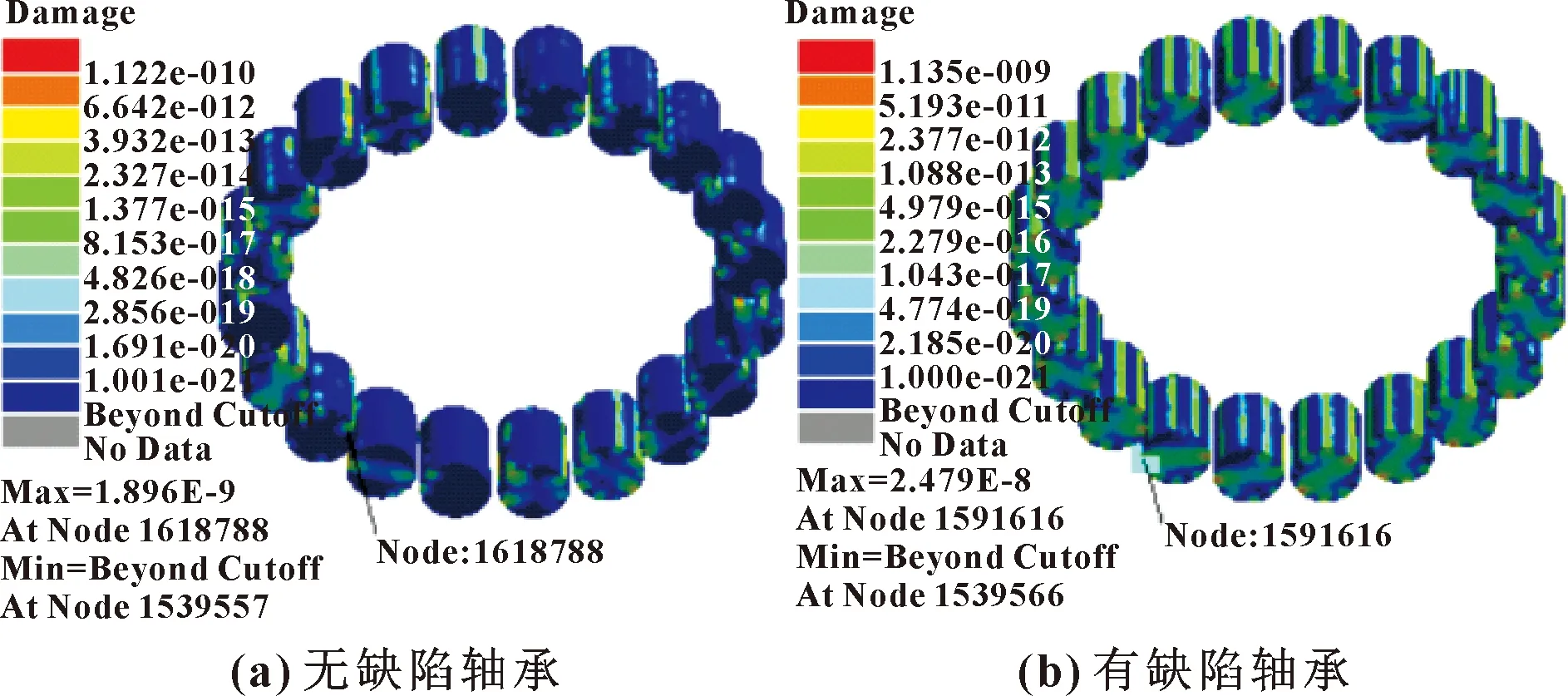
图13 圆柱滚子损伤云图
由图13、图14可知:无缺陷轴承的圆柱滚子在节点N1618788处发生损伤,其最大损伤为1.896×10,在该节点处最小寿命为5.274×10次,而多数损伤在4.826×10~2.327×10,与之对应的疲劳寿命为2.072×10~4.297×10次;有缺陷轴承的圆柱滚子在节点N1591616处发生损伤,其最大损伤为2.479×10,在该节点处最小疲劳寿命为4.034×10次,而多数损伤在1.043×10~1.088×10,与之对应的疲劳寿命为9.587×10~9.192×10次。可知大多数损伤发生在两轴承的圆柱滚子与内、外圈接触面上,与动力学仿真轴承的圆柱滚子受到的等效应力集中的位置相符合,进一步可以推测出轴承失效的区域。

图14 圆柱滚子寿命云图
3.3.3 外圈疲劳分析
图15、图16所示分别为无缺陷轴承和有缺陷轴承外圈的损伤和疲劳寿命云图。
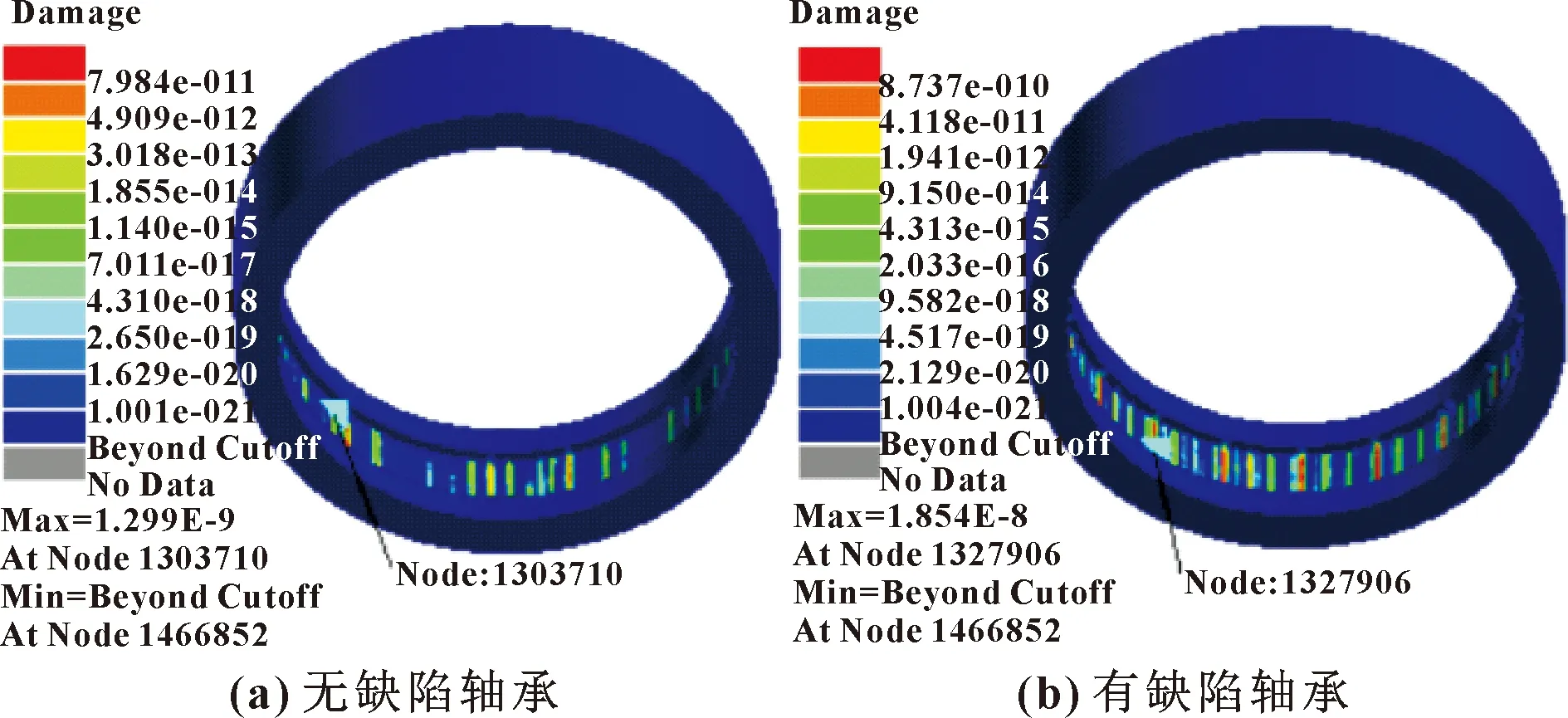
图15 外圈损伤云图

图16 外圈寿命云图
由图15、图16可知:无缺陷轴承的外圈节点N1303710处发生损伤,其最大损伤为1.299×10,该节点处最小寿命为7.700×10次,而多数损伤在4.310×10~1.855×10,与之对应的寿命为2.320×10~5.390×10次;有缺陷轴承的圆柱滚子在节点N1327906处发生损伤,其最大损伤为1.854×10,在该节点处最小寿命为5.395×10次,而多数损伤为9.582×10~9.150×10,与之对应的疲劳寿命为1.044×10~1.093×10次;外圈大多数损伤发生在与滚子的接触面上,这与动力学仿真结果相符合。根据圆柱滚子和外圈疲劳分析,轴承失效发生在滚子的内、外圈滚道上。根据外圈的疲劳寿命云图还可以看出,外圈有缺陷的轴承使用寿命比无缺陷轴承的寿命小。
3.3.4 不同转速时轴承寿命分析
基于所建立的不同局部剥落缺陷轴承的模型,分别进行动力学仿真疲劳、寿命计算,得到各轴承部件在不同转速下的疲劳寿命,分别如图17—图19所示。可知:随着转速增加,各轴承部件的疲劳寿命逐渐下降;随外圈局部缺陷尺寸不断增加,轴承各部件疲劳寿命呈下降趋势。

4 总结
对有局部剥落缺陷轴承和无缺陷轴承进行显式动力学和疲劳寿命分析,得出以下结论:
(1)无缺陷轴承滚子节点应力波动较小,而有局部剥落缺陷轴承滚子经过外圈缺陷时,与外圈缺陷边缘接触,节点应力会有剧烈的波动;
(2)转速不断增加时,两类轴承各部件的等效应力均呈上升趋势,有缺陷轴承各部件的等效应力均比无缺陷轴承的等效应力大,随着缺陷尺寸不断增加,缺陷轴承各部件的等效应力也逐渐增大,从而缩短了疲劳寿命;
(3)在相同转速时,无缺陷轴承的各部件寿命均比有局部剥落缺陷轴承长;转速不断增加时,两种轴承的各部件疲劳寿命均呈不同程度的下降趋势;由于外圈存在局部剥落缺陷,随缺陷尺寸不断增加,外圈疲劳寿命急剧下降。

