基于相似性与GA-RF的航空发动机剩余寿命预测
赵洪利,魏凯
(中国民航大学航空工程学院,天津 300300)
0 前言
航空发动机是飞机中高度复杂的部件之一,且一般工作在高温、高压、高转速、高负荷等严苛条件下,其可靠性与安全性一直备受关注。对于发动机机队的管理,航空公司既想保证发动机在役的安全性、可靠性,又想降低发动机的维修成本,而预测与健康管理(Prognostics and Health Management, PHM)是一个有效的解决方案。PHM结合了传感器性能参数监测、数据采集、故障诊断以及寿命预测等方法实现设备的视情维修,提高系统的安全性与可靠性。
大多数学者都采用单参数来表征发动机性能退化过程,或将发动机所有的传感器测量参数进行融合构建健康指数,但难以准确表征发动机真实的衰退过程,且大多利用传统的智能模型进行建模,相比而言集成模型具有较好的非线性逼近能力,能处理复杂度较高的问题。因此,本文作者提出一种融合数据构建发动机健康指数,结合多模型相似性匹配与集成模型进行发动机剩余寿命预测的方法。首先,结合层次聚类和轮廓系数,选择发动机部分传感器测量参数,融合发动机健康指数来表征其性能退化过程,这样既解决了单一参数不能准确表征发动机性能退化过程的问题,又降低了利用所有传感器参数进行数据融合带来的高维度运算;其次,采用遗传算法优化随机森林训练发动机性能退化模型,并结合多模型相似性匹配优化发动机剩余寿命预测结果,提高预测精度;最后,在某涡扇发动机仿真数据集中,验证所提出方法的有效性。
1 发动机健康指数构建
由于发动机性能衰退模式不尽相同,单一参数不能准确表征发动机性能退化过程,本文作者采用融合数据构建发动机健康指数,并对选择的特征参数进行卡尔曼滤波、平滑与归一化处理。
1.1 融合特征选择
层次聚类(Hierarchical Clustering)是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在树状图中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法。对数据进行层次聚类,通常要使用欧几里德距离作为度量。在进行层次聚类之前,应对所有的特征参数进行规范化处理,以消除量纲不同而产生的影响。文中也使用欧几里德距离作为度量,其公式如下:

(1)
其中:为维空间中点(1,2,…,)和点(1,2,…,)之间的欧几里德距离。层次聚类不需要预先设定数据分类数目,它能按照不同的距离将数据进行最优分类,相比其他的聚类算法,它更适合发动机数据集分类及特征选择。
1.2 构建健康指数
在所选择的发动机传感器测量参数滤波与平滑后,通过实时数据与失效数据作差,将数据处理为增量Δ:
Δ=-
(2)
式中:表示实时特征数据;表示失效特征数据;为融合特征的个数。将数据进行整体归一化处理,以消除数据量纲和量级的影响,其基本公式如下:
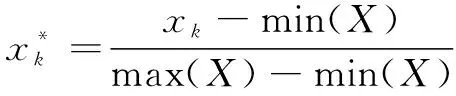
(3)
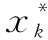

(4)
式中:为健康指数的时间序列长度;为每个特征所占的权重值,融合的权重值为单个特征参数所占总方差大小,公式如下所示:
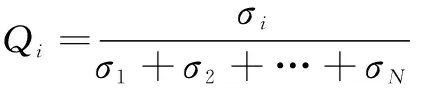
(5)
其中:为第个特征参数的方差,1≤≤。
2 剩余寿命预测模型
在发动机剩余寿命建模中,大多数研究者仅使用一个模型训练发动机性能衰退过程,但这样的模型难以准确拟合发动机的衰退过程。鉴于发动机由多个不同的单元体组成,不同工作状态下单元体的状态各不相同,即使同型号的发动机,其性能衰退模式也不尽相同,所以本文作者选用集成模型随机森林训练发动机性能退化过程。
2.1 随机森林模型
随机森林是将自举汇聚法(Bagging)与随机子空间方法相结合的一种集成学习模型,并在Bagging的基础上引入了随机性,能更加准确地表征发动机之间的差异性。作为集成学习模型,随机森林使用了两种集成策略:Bagging策略和改变输入特征策略。Bagging策略使用Bootstrap采样方法,集成每个基础学习模型。对于每一个基础学习模型,采用有放回抽样获得其训练样本,由于采样的随机性,各个基础学习机的训练样本集合不尽相同,每个基础学习模型同时训练,最后将所有基础学习机的结果集成后,作为集成学习模型的输出。因此,每个基础学习机在Bagging策略中是并联关系,其流程如图1所示。
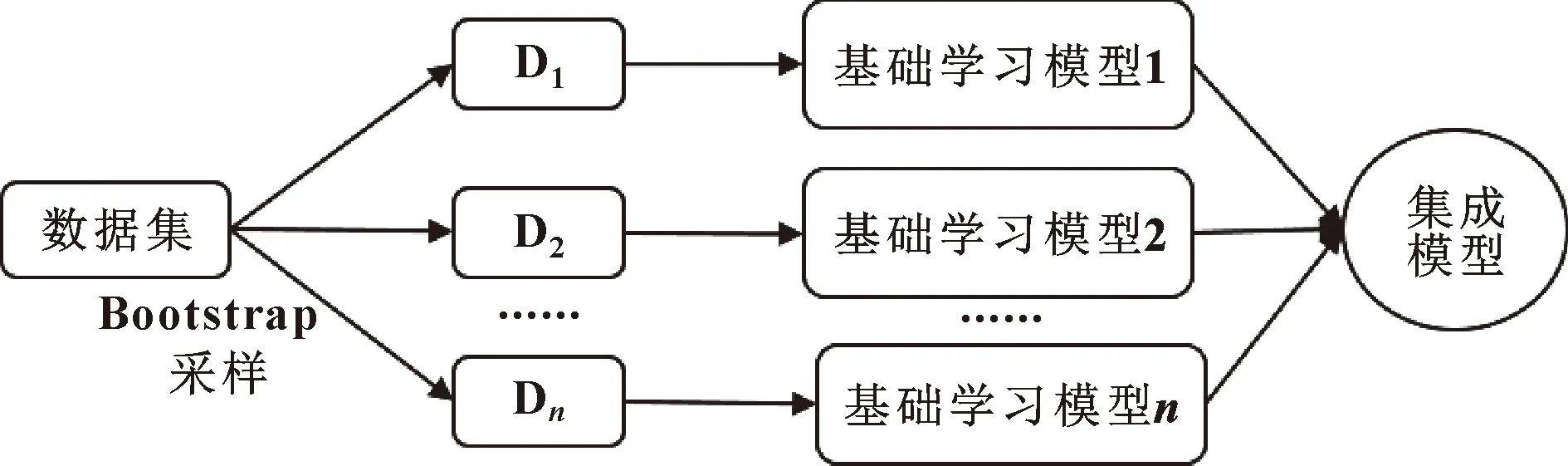
图1 Bagging集成策略
随机森林模型的基础学习模型为决策树,或称为分类树或回归树(Classification and Regression Tree,CART),在文中发动机剩余寿命预测是回归问题,所以图中基础学习模型特指回归树,其流程如图2所示。对航空发动机剩余寿命进行预测时,将当前发动机健康指数同时输入到个回归树中,便得到个剩余寿命预测值,即每个回归树对当前发动机剩余寿命进行了估计,然后取个输出值的平均值作为随机森林模型的最终输出值,便得到随机森林模型对当前发动机剩余寿命的估计。
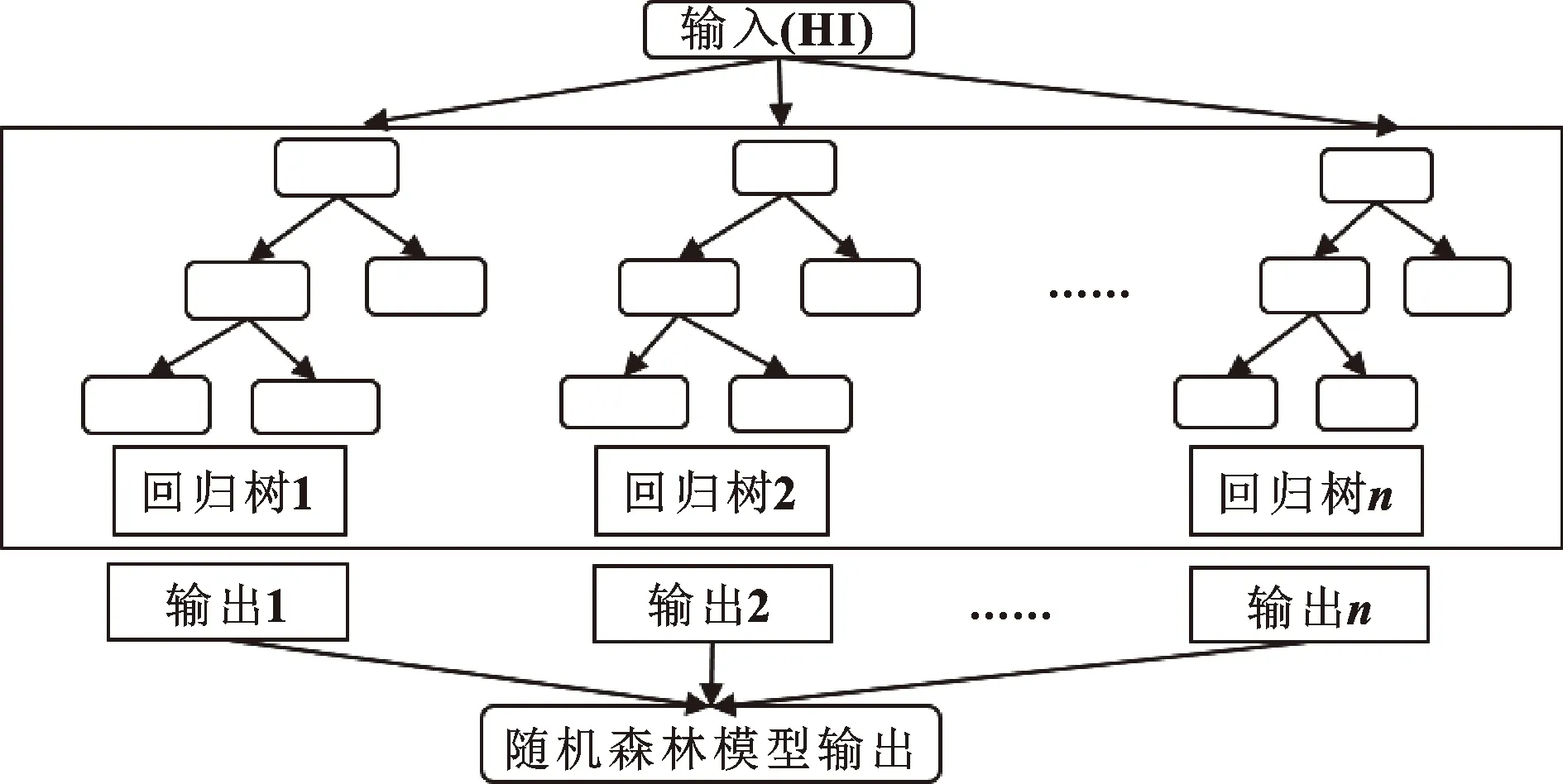
图2 随机森林模型
2.2 GA-RF模型
随机森林算法中需调整的参数较少,本文作者选择4个重要参数进行寻优,分别为回归树的数目、每个节点处的特征数目、树的最大深度、节点信息增益大小。随机森林模型对这4个参数的取值并不敏感,而且一般不会过拟合,这也是本文作者选择随机森林模型进行优化的原因。超参数寻优迭代过程如下:
(1)设定目标函数及优化超参数的取值范围,文中选择预测值与真实值的均方根误差(RMSE)作为目标函数;
(2)设定遗传算法最大遗传次数、染色体选择方法、重组方法、交叉方法、变异方法以及重组概率、交叉概率、变异概率;
(3)初始化遗传算法种群,生成种群染色体矩阵,计算种群个体的目标函数值,根据目标函数值的大小为每条染色体分配适应度,记录当代最优个体;
(4)对染色体种群进行选择、重组、交叉、变异等进化处理,再将进化后的新一代个体代入随机森林模型进行训练,计算个体目标函数值,根据公式分配适应度,记录当代最优个体;
(5)设置迭代终止条件,如果在迭代过程中满足条件,则停止计算并获得最优染色体,否则返回步骤(4)并继续该过程。
2.3 相似性与GA-RF模型
传统的发动机剩余寿命预测方法通常直接将数据代入回归模型,或通过相似性公式计算当前发动机与历史发动机的距离,来计算发动机的剩余寿命。文中则采用多模型相似性匹配与回归建模相结合的方法预测发动机剩余寿命,利用多模型相似性匹配优化回归模型的预测结果,与之不同的是本文作者将相似性用于回归模型,找出与当前发动机性能退化最匹配的若干模型,预测当前发动机的剩余寿命。通常大多数研究者将相似性用于回归建模前,通过相似度在历史样本中找出与当前发动机最相似的某些发动机进行实例重用。但是,此方法常会出现当前预测发动机的运行循环超出历史发动机总循环的情况,降低模型匹配的精确性。将相似性用于回归建模后可以避免出现上述情况,从而提高发动机剩余寿命预测精度。发动机剩余寿命预测模型如图3所示。

图3 发动机剩余寿命预测模型
预测具体步骤如下:首先,利用GA-RF算法对历史发动机进行性能退化模型训练;然后,根据当前循环预测值与真实值误差选择若干匹配的模型,即误差小的相似度大,误差大的相似度小。其中,误差公式为

(6)
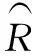

(7)
式中:、为所选样本序号,且1≤、≤;为所选模型数量。计算预测发动机的剩余寿命,公式如下:
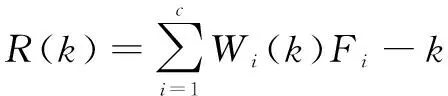
(8)
式中:为第台历史发动机的全寿命;为第台发动机所占的权重;()为预测发动机第循环时的剩余寿命。
3 实例验证
3.1 数据集描述
选用某涡扇发动机公用测试数据集对所提出的预测方法进行验证,其仿真数据集由NASA使用Commercial Modular Aero-Propulsion System Simulation软件模拟生成,一共包含4组数据集,每组数据包含训练集与测试集。文中使用第1组FD001数据集来预测发动机剩余寿命。该数据集是在单一工况和单一故障模式下生成的,包含100台全寿命训练数据,每台发动机包含24个监控参数,其中21个为含噪声的性能退化数据,3个为工况数据。21个发动机性能监控数据主要为温度、压力、转速、燃油流量等;3个工况数据为飞行高度(Altitude)、飞行马赫数(Mach)以及油门杆解算角度(TRA)。发动机结构如图4所示。
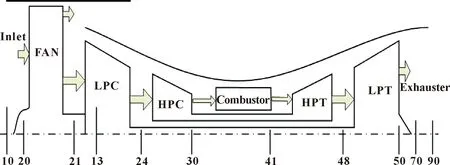
图4 C-MPASS发动机结构示意
3.2 发动机健康指标构建
本文作者先从发动机21个传感器数据中,利用方差过滤选出有变化的14个传感器测量参数,并在这14个有变化的参数中选择部分参数进行融合。首先,对14个有变化的发动机参数进行层次聚类,结果如图5所示。
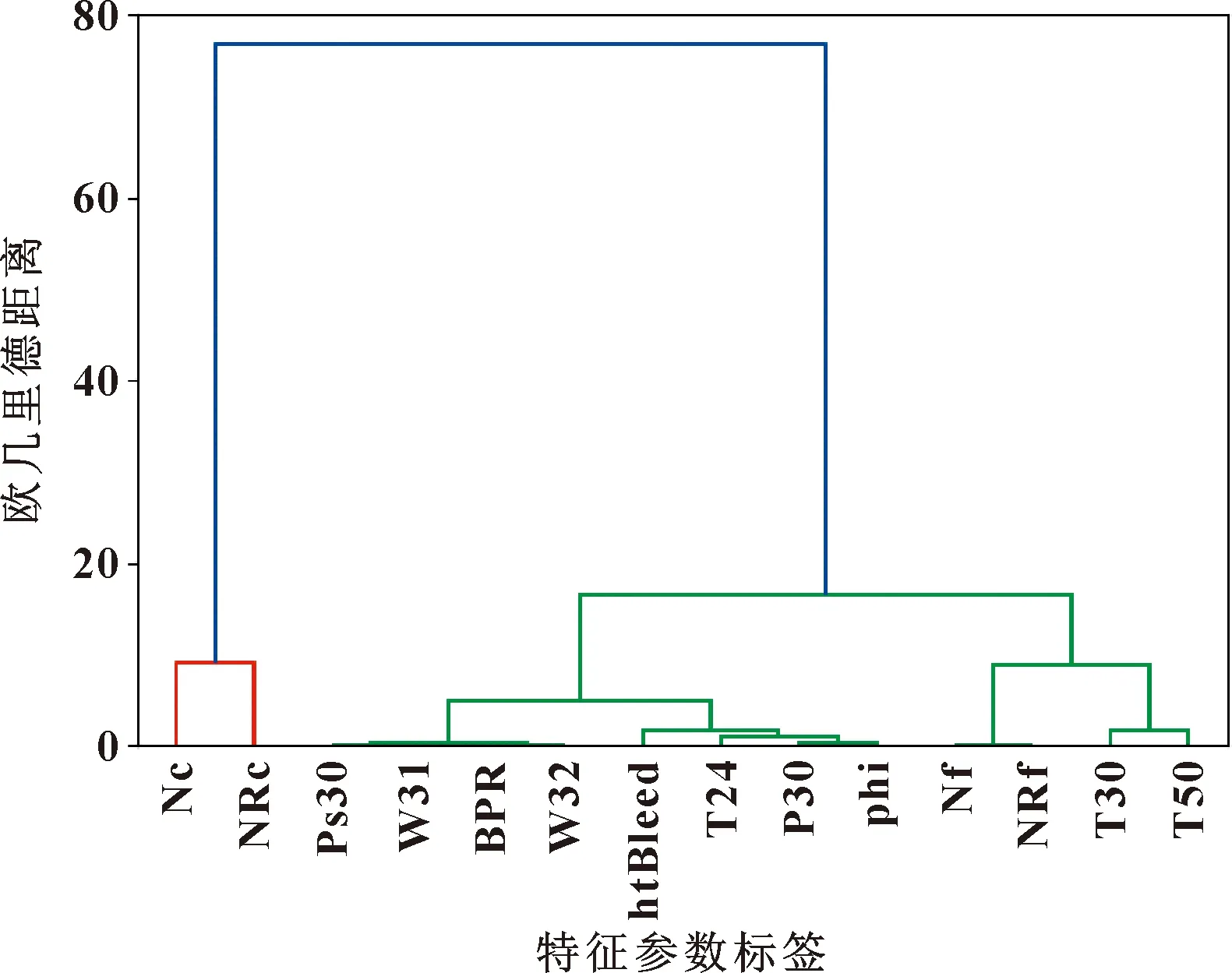
图5 特征参数层次聚类
从图5可知,在不同距离下,数据被聚为不同的类。为精确聚类最佳的数目,引入轮廓系数:
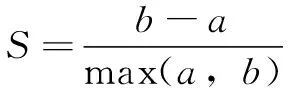
(9)
式中:为特征与其自身所在簇中其他特征的相似度;为特征与其他簇中特征的相似度。由公式(9)可知,的取值范围为(-1,1),其值越接近1说明聚类的效果越好。在分别将数据聚类为2~13簇的情况下,分别求其对应的轮廓系数。对比发现,在数据被分为5簇时,轮廓系数均值最高为0.86。图6所示为数据被分为5簇时,簇内特征的轮廓系数,其中虚线为轮廓系数平均值0.86。可见:将数据分为5簇时,每簇特征的轮廓系数均非常接近平均值,聚类效果最佳。
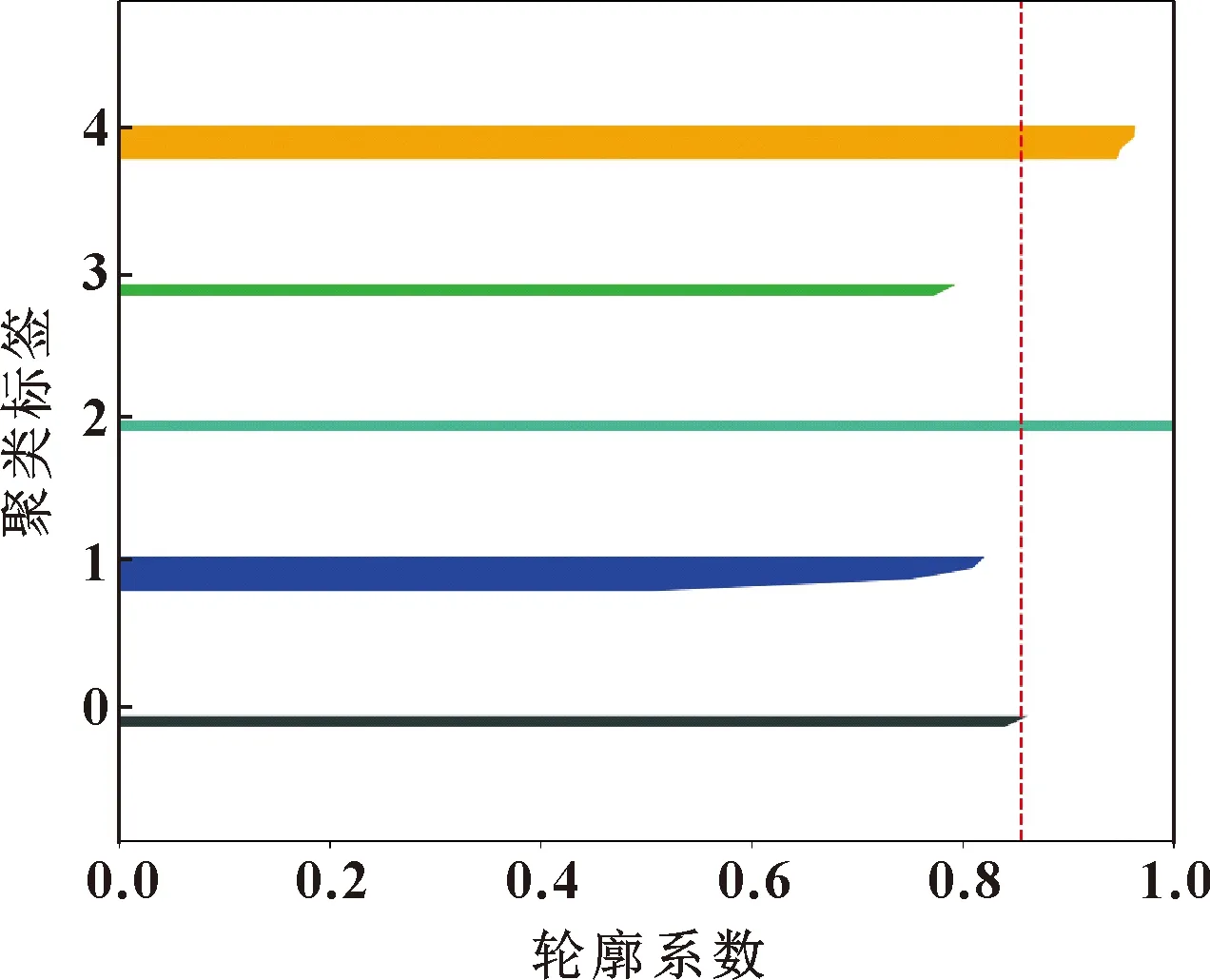
图6 聚类特征轮廓系数
由于聚类算法会使得同组之间的数据相似度大,而不同组之间的数据相似度小,所以从每组中选择一个特征进行融合,结合对航空发动机专业知识以及文献[16]的相关研究,最终选择5个发动机性能退化数据进行融合。所选融合参数如表1所示。

表1 发动机融合特征参数标签
为减少数据噪声的波动提高训练效率,本文作者采用卡尔曼滤波与平滑对所选的特征参数进行消除噪声处理,使得数据更加真实。以发动机EGT特征为例,进行原始数据、数据滤波与平滑前后的可视化,结果如图7所示。其中,圆点数据为传感器测量数据,虚线是滤波后的发动机排气温度,实线是对滤波后的数据进行平滑。由此可见,对特征进行卡尔曼滤波与平滑后极大地消除了数据的噪声,使得数据更接近真实值。
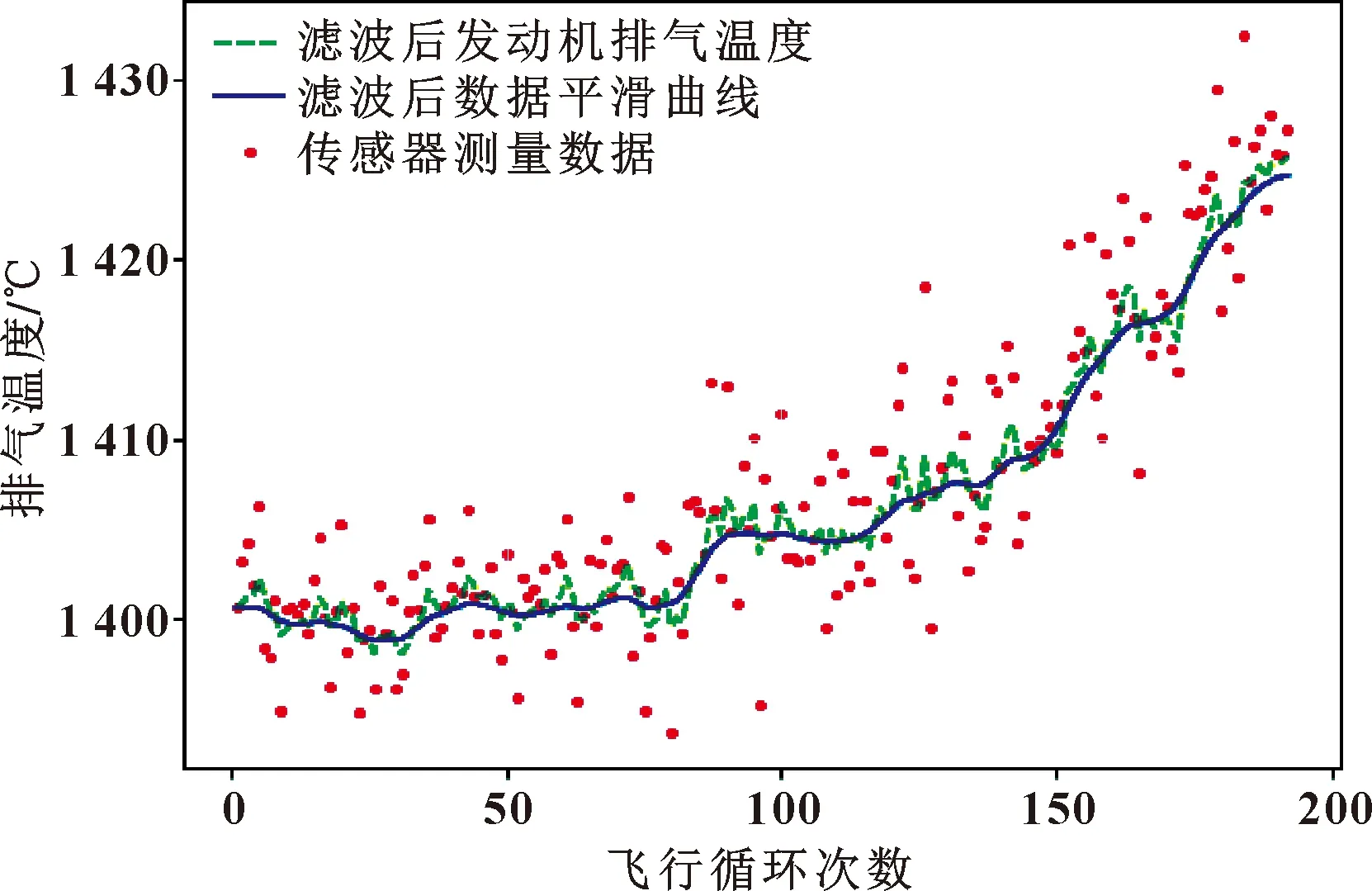
图7 发动机排气温度特征滤波与平滑
滤波平滑后对所选的特征进行增量与归一化处理,消除数据间的量纲影响。选取前80台发动机数据作为训练集,后20台作为测试集。并选取所有训练集中此特征最后一位数据的均值作为其失效值,按公式(4)计算出80台训练集的健康指数,HI变化趋势如图8所示,它直观地表示出了发动机的性能退化过程。可知:发动机在前期没有发生故障,健康指数保持相对恒定,说明发动机性能在早期保持在稳定水平,性能退化并不明显;然而,随着发动机的运行和高压压气机性能衰退,发动机性能开始出现衰退,在运行到大约120次循环后发动机性能开始出现明显的衰退,健康指数下降明显。

图8 发动机健康指数
3.3 实验预测结果与分析
发动机的性能衰退状态与其剩余寿命具有一定的映射关系,由于发动机前120次循环健康指数变化不大,对发动机运行前期的剩余寿命预测意义不大。因此,从120次循环开始预测发动机剩余寿命。将80台发动机训练数据集代入GA-RF模型进行训练,其中遗传算法优化的部分模型的最优参数如表2所示。

表2 模型参数寻优结果
在模型训练后,以第100台发动机为例进行预测结果可视化。在预测结果评价方面,选用均方根误差(RMSE)、绝对误差(MAE)、预测误差率(Prediction Error Rate,PRE)对发动机剩余寿命预测结果进行评价,公式如下:

(10)
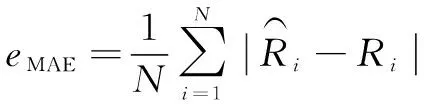
(11)

(12)
其中:为样本序号,1≤≤;为发动机当前循环数。以发动机运行到第180次循环时为例,通过相似度排序选择相似度最高的8台发动机作为加权样本,即选择第43、1、72、4、26、44、55、76号发动机作为加权样本。通过误差加权公式(7)计算得到第100台发动机180次循环时,相似样本权重如表3所示。

表3 发动机下发寿命预测权重
该发动机实际下发时间为200次循环,剩余寿命为20次循环,通过剩余寿命预测公式(8)计算得到剩余寿命为15.65次循环,预测误差率为2.41%,总的预测均方根误差为6.508 8。同样,将相似性与GA-RF相结合,计算当前发动机120~200次循环的和误差率。图9和图10所示分别为第100台发动机120次循环后的剩余寿命预测值与真实值的对比以及误差率。

图9 第100台发动机剩余寿命预测结果 图10 第100台发动机剩余寿命预测误差率
由图9可知:在预测早期阶段,由于数据量较少及发动机性能退化不大预测误差较大,但随着发动机运行数据的增多,在发动机运行后期预测误差逐渐减小,越来越接近真实值。由图10也可以看出:在此发动机140次循环后预测误差率逐渐下降,且整体均稳定在0~0.1之间。其余部分发动机预测结果如表4所示。为验证所提出的多参数融合健康指数比单一参数能更准确表征发动机的性能衰退过程,表4中还随机给出了5台发动机单参数多模型(EGT)预测与融合健康指数(HI)后多模型预测发动机剩余寿命结果对比,以及融合健康指数后多模型预测与单模型预测发动机剩余寿命结果对比。可知:基于单参数多模型匹配预测发动机剩余寿命均值为9.194、均值为8.765;基于融合健康指数单模型预测发动机剩余寿命均值为7.793;均值为6.431,基于融合健康指数多模型匹配预测发动机剩余寿命均值为6.128、均值为4.901,可见所提出的数据融合的方法是有效的,且融合健康指数和多模型相似匹配极大地提高了发动机剩余寿命预测精度。
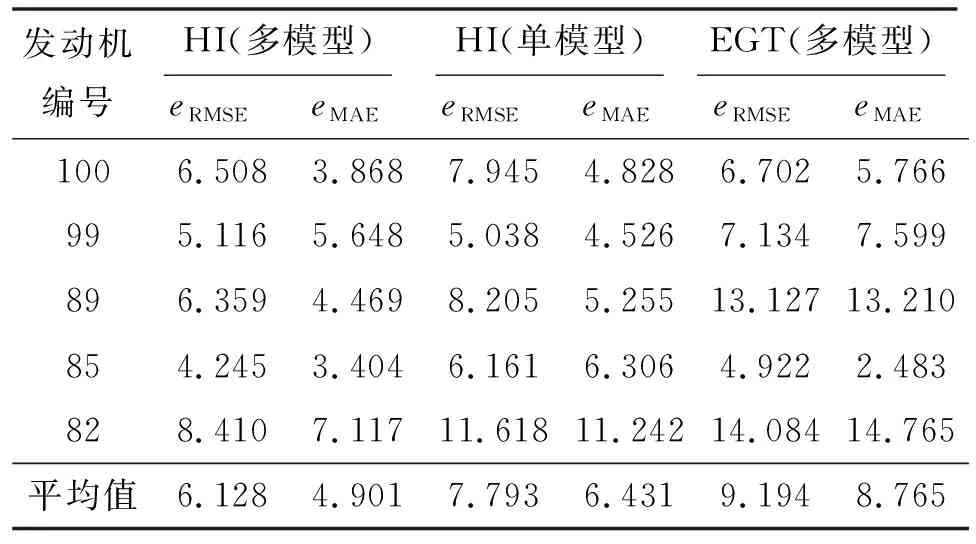
表4 剩余寿命预测结果对比
4 结论
(1)本文作者采用层次聚类等方法筛选出需要融合的参数,实现性能数据的高效、综合利用。再将单个特征占总方差比为权重,将选定的特征参数进行融合,有效地构建了发动机健康指标,克服了利用单一参数不能准确表征发动机性能退化等问题。
(2)采用集成模型随机森林训练发动机性能衰退模型,能更好地拟合航空发动机的实际退化过程;引入遗传算法对模型的超参数寻优,并将多模型相似性匹配与GA-RF模型相结合,对回归模型的预测结果进行优化,极大地提高了发动机剩余寿命预测精度。
(3)所提方法在C-MPASS数据集的训练与预测中取得了较好的结果,均值为6.128、均值为4.901。研究结果为利用同类型发动机数据进行剩余寿命预测提供了参考。

