GeoGebra在高中回归模型教学活动中的应用探究

◎王新爱 李伟斌 （兰州市第四中学，甘肃 兰州 730050）

一、GeoGebra在高中回归模型教学中的应用价值

1.数学建模活动的概念

在高中阶段数学课程中，数学建模活动是用数学的眼光发现问题现实生活中的实际问题，用数学语言概括抽象出问题，并用数学符号、语言表达问题，再用数学方法分析问题，构建模型解决问题的过程.数学建模活动的主要环节大致可以概括为：了解问题的实际背景，提炼出数学问题；对问题进行合理假设和简化，找准建模的核心问题；辨别问题类型，构建数学模型；选择恰当的数学工具进行推理运算，求解模型；分析检验结果，改进模型；最终解决实际问题（图1）.因此，数学建模活动是学生综合运用所学知识、技能，以数学模型为载体，解决实际问题的一类综合实践活动，是高中阶段数学课程的重要内容.

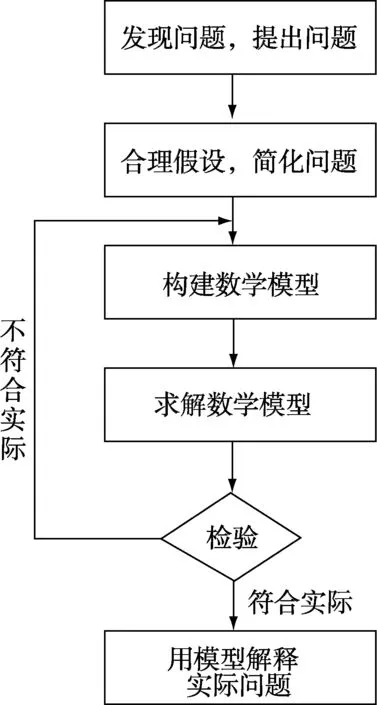
图1

高中数学建模活动中的数学模型，从课程内容的角度划分可以分为很多类型，包括函数模型、方程（组）模型、不等式（组）模型、数列模型、立体几何模型、解析几何模型、向量模型、概率模型、统计模型等.本文所论述的回归模型可以看作是函数模型与统计模型结合的一类综合模型，建立回归模型的方法是回归分析，其基本步骤为：确定研究对象，明确解释变量和预报变量；画出两个变量的散点图，观察它们之间是否具有相关关系（线性相关或非线性相关）；依据数学经验选定回归方程的类型；运用恰当的数学方法估计回归方程中的参数；用残差图和相关指数分析模型，选定拟合效果最好的回归模型类型，并运用回归模型进行变量预测.

2.数学建模活动在高中阶段数学课程中的地位

新一轮基础教育课程改革对于高中数学课程内容进行了安排，已将数学建模活动与数学探究活动单独设为一个主题，凸显了数学建模课程的重要地位.具体来看，新课标课程的结构安排，不仅在必修课程和选择性必修课程中分别设置了数学建模活动与数学探究活动主题，而且在其他主题内容中也相应穿插了适应于内容的数学建模活动专题.《普通高中数学课程标准（2017年版2020年修订）》中指出，数学学科核心素养包括以下六个方面内容：数学抽象、数学建模、逻辑推理、数学运算、直观想象和数据分析.在这六个学科核心素养中，数学建模素养是其他数学核心素养的综合体现，具体表现在：在建模准备阶段，学生需要运用数学抽象、直观想象素养以数学的眼光发现实际问题，抽象提炼出数学问题，抓住核心问题完成模型的分析，确立模型类型；在建模建立阶段，学生需要具备数据分析的素养，完成必要资料数据的收集与整理；在模型求解和检验阶段，学生要具备良好的逻辑推理素养，用于探究和表述论证过程，完成相应数学运算求解数学问题.因此数学建模问题往往具有综合性强、系统性强、实践性强、多学科融合等特点，是高中阶段数学课程中发展学生数学学科核心素养的重要途径.

3.GeoGebra在高中回归模型教学中的应用价值

高中阶段，数学建模活动以课题研究的形式开展，其难度大、周期长、要求高的特点，对教师的教学方法提出了新的要求，也对学生的学习能力提出了极高的要求.因此，教师将GeoGebra软件创新性地运用于教学活动中，用以解决高中回归模型教与学的困境，在这一环节中GeoGebra软件就显得很有价值.

GeoGebra是一款功能强大的数学教学软件，教师在高中回归模型的教学过程中，一方面可借助GeoGebra强大的运算功能，将教学过程中的一些非核心的问题，例如，整理数据、绘制图形、逻辑运算等问题，交由软件进行辅助处理，可有效解决建模活动周期过长、学生计算量过大的痛点，增强教学活动的连贯性，提高课堂教学效率和学生学习效率.另一方面，GeoGebra使用简单，交互性强，学生经过简单学习就可以完成大部分操作.因此，教师将其作为学生学习活动中认知、探究数学问题的一种工具，可以有效解决数学建模课程中部分学生参与度不高，兴趣不强的问题，还有助于培养学生的数学应用意识，提升动手实践能力，增强创新意识和科学精神.

二、GeoGebra在回归模型教学活动中的应用举例

“水温变化”问题是高中函数模型教学过程中的一个经典问题，在人教版新旧两个版本教材中都有不同形式的呈现.在旧版教材中该问题作为一个开放性的探究内容，放置于信息技术应用板块，而在新版教材中，该问题加入了中国茶文化的背景，介绍了建立函数模型的详细过程.对比发现，两版教材中所建立的函数模型是不同的.因此，教师可将该问题稍加改编，得到一个回归模型教学的绝佳案例.

中国茶文化博大精深.茶水的口感与茶叶类型和水的温度有关.经验表明，某种绿茶用85℃的水泡制，再等到茶水温度降至60℃时饮用，可以产生最佳口感.那么在25℃室温下，刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感

我们直接利用教材提供的数据：

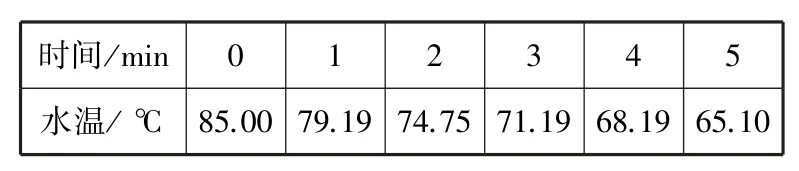
时间／min 0 1 2 3 4 5水温／℃85.00 79.19 74.75 71.19 68.19 65.10

设茶水温度从85℃开始，经过min后的温度为℃.新版教材建立的函数模型（后简称模型一）为＝60×0.9227+25（≥0），该函数模型本文不再加以详细论述，后文将直接引用.本文将以旧版教材选择的函数模型（后简称模型二）＝e+（≥0）的建立过程为例，具体探讨一下GeoGebra在回归模型教学活动中的应用.

1.GeoGebra在模型准备过程中的应用

学生会有这样的生活常识：一杯热茶放置于室温中，其温度变化程度与放置时间有关.在建模活动中，教师辅助学生利用计算机、数据收集器、温度传感器等信息技术工具收集水温变化数据，利用GeoGebra绘制时间和茶水温度的散点图（图2），可以发现，时间和茶水温度具有非线性相关关系.现实生活中，影响茶水温度的变量有很多，为简化模型，做出如下两点假设：假设室温一直保持不变为25℃；假设茶水置于室温空气中，任一时刻茶水温度（℃）对时间（min）的变化率只与该时刻茶水和室温成正比，与其他因素无关.

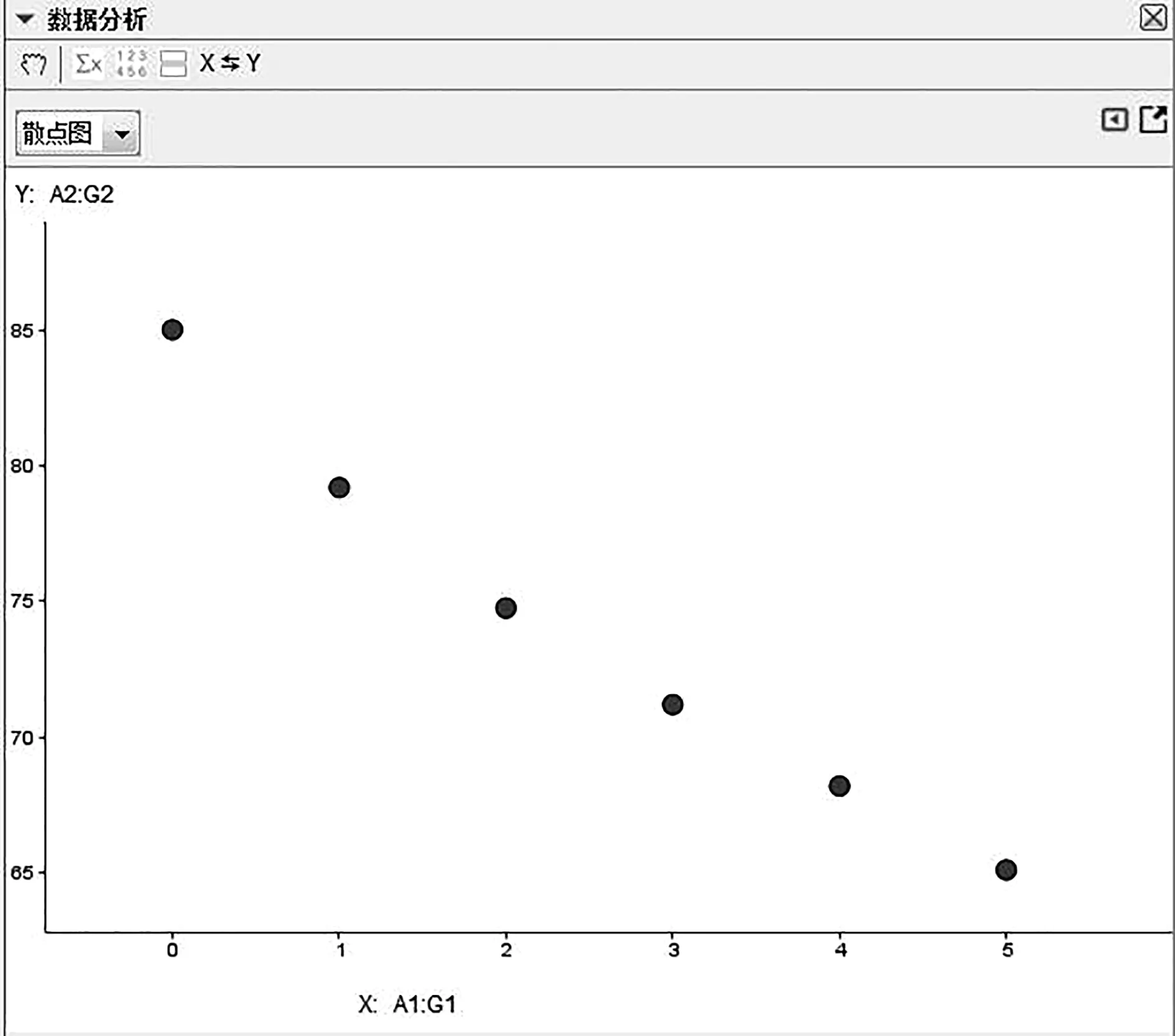
图2

图3

2.GeoGebra在模型建立过程中的应用

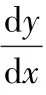
将上式变形为ln（-25）＝+ln，利用GeoGebra绘制以和ln（-25）为坐标的散点图（图3）.可以看出，数据取对数以后基本满足线性关系，因此得到时间和温度的对数线性模型.

3.GeoGebra在模型求解过程中的应用

在GeoGebra中选择双变量回归分析，在回归模型中选择线性，对上述对数线性模型求解得ln（-25）＝-0.0791+4.0784（图4），变形即可解得函数模型为＝e+25（≥0）.在此过程中，如还有必要提升学生的数学运算素养，教师也可给学生提供关键数据，让学生练习运用最小二乘法计算求解相关参数.

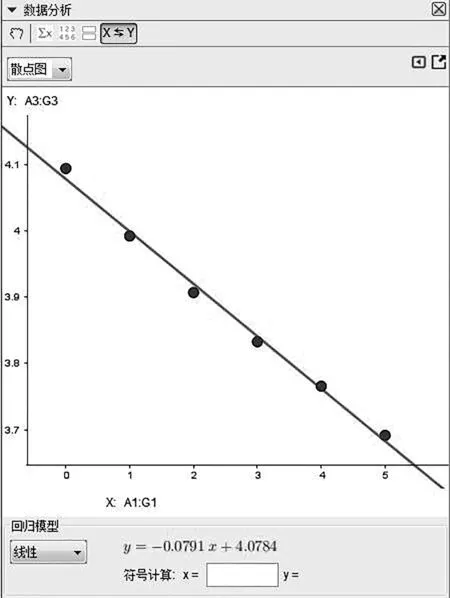
图4

4.GeoGebra在模型检验过程中的应用

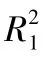
图5

通过上述过程可以看出，教师借助GeoGebra解决回归模型问题非常简便高效，学生可直观详细地观察建立回归模型活动的各个环节.

三、GeoGebra在回归模型教学活动中的应用思考

在传统的回归模型教学活动中，学生不仅要快速学习理解诸多新概念，还要进行大量的作图与计算工作，使得学生在学习过程中总感觉“被牵着鼻子走”，学习不够深入，参与感不强.GeoGebra的引入，完全可以解决学生在学习活动中遇到的这些难题，让学生将更多精力放到教学活动的主线内容，去繁就简，把握教学内容的本质.教师可采取翻转课堂、对分课堂等多种教学模式，让学生在GeoGebra平台上进行数学实验，主动参与到建模活动的各个环节，引领学生完成深度学习，获得有意义的学习过程，促进学生学习能力和实践能力的发展.

高中数学教学要注重信息技术和课程内容的深度整合，应用信息技术实现知识生活化，提高教学效率，在数学建模活动中，也应当鼓励学生多使用信息技术完成课堂探究活动.同时，教师在教学中也要注意教学过程不可本末倒置，过于重视信息技术，而丢失了教学内容的本质.上述回归模型教学的教学目标是使学生经历建立回归模型活动的全过程，在此过程中提升学生的数学建模、数据分析、数学运算等素养.而借助GeoGebra等教学软件，有些学生可能会不经过任何分析与运算就能直接给出拟合函数，这显然不符合本节课的教学目的，因此在实际教学过程中，教师要多加以引导.

回归模型活动要达到较好的预期效果，前期的准备工作一定要充分.以上述案例为例，学生需要花一点时间进一步理解一些物理学概念，了解一点高等数学的内容，与同学合作完成数据的收集，也要熟悉一下GeoGebra软件的相关操作方法.因此在活动准备阶段，教师要看实际情况给予学生足够的帮助.