Jacobi 四次曲线的快速差分加法公式*

吴宏锋， 宋贞贞

北方工业大学 理学院， 北京 100144

1 引言

域K上的椭圆曲线定义为域K上的一维阿贝尔簇. 一般把椭圆曲线的方程写成Weierstrass 方程

其中a1，a3，a2，a4，a6∈K. 椭圆曲线的点乘或标量乘运算， 就是给定椭圆曲线上一个点P和一个正整数k， 计算k个点P的和[k]P， 它是所有基于椭圆曲线的各类密码协议中的核心运算. 改进点乘的运算效率有多种途径， 其一就是在不同的曲线模型上构造更加快速的计算公式. 有很多种椭圆曲线的表示模型， 诸如Edwards 曲线[1]、Jacobi 四次曲线[2]或Jacobi 相交曲线[3]等等. 不同的曲线模型有各自的优点和特殊应用.

早在Jacobi 时代， 人们就研究过形如y2= (1-x2)(1-k2x2) 的椭圆曲线， 其中k/= 0，±1. 该类型的椭圆曲线可由Jacobi 椭圆函数参数化， 一个点P= (x，y) 可以参数化表示为(sn(u)，cn(u)dn(u))，因此易于得到它上的加法公式. Jacobi 四次曲线在密码学相关领域中的研究始自Chudnovsky 和Chudnovsky[4]. 他们首先在曲线y2=x4+ax2+b上使用权射影坐标提出不使用逆运算的点加和倍乘公式. Billet 和Joye[2]则在一般的Jacobi 四次曲线Y2=dX4+2aX2Z2+Z4上提出了更加快速的统一(unified) 点乘公式， 也就是说， 该运算公式不区分两个点是不是相同. Duquesne[5]则进一步改进了该点乘公式的效率. Hisil 等人[6-8]则引入了一系列的不同坐标表示和快速的倍乘和统一加法公式. 关于Jacobi 四次曲线的发展历史可以参考文献[2，6].

Montgomery[9]最早提出了一种简单的被称为Montgomery 阶梯(ladder)的Montgomery 算法. 在Montgomery 算法的每一步中， 都需要计算点加和倍乘运算， 因此该算法还抵抗简单的能量攻击. Montgomery 算法使用差分加法(differential addition) 和倍乘公式， 能有效地提高点乘运算的效率. 该算法的关键是在计算过程中始终保持两个点的差不变.

提高点乘运算效率是通过缩减点乘运算中基本的有限域运算的次数实现的. 表示有限域运算花费多少的基本运算包括有限域上元素的乘法运算(记作M)， 平方运算(记作S) 及一个常数和其它有限域元素的运算(记作D). 在Montgomery 曲线上执行差分加法运算， 不需要所有的坐标都参与， 在仿射情形下只需要使用点的x-坐标即可完成整个运算， 当然， 如果需要可以在最后的时候恢复最终计算结果的其它坐标. 在射影坐标下， 可以使用(X:Z) 两个坐标而不引入Y坐标参与计算， 从而达到不使用计算消耗很大的有限域元素求逆运算的目的. 这种使用部分坐标参与计算的技巧不仅减小了空间存储规模， 更有利于资源受限环境下的实际应用， 而且提高了点乘运算的效率. 正是基于此， 人们也研究其它曲线模型上的快速Montgomery 差分加法算法. 诸如扭Edwards 曲线上的差分算法[10]、Jacobi 四次曲线上的差分算法[11]. Jacobi 四次曲线上的混合加法和倍乘运算的最快记录是由Hisil[6]获得的， 加法和倍乘运算的花费分别是6M+3S+1D和2M+5S. 但这些公式需要六个坐标参与表示一个点. 顾海华等人[11]首先研究了Jacobi 四次曲线y2=k2x4+2ax2+1 上的差分加法公式， 在计算过程中只需要点的(X:Z) 坐标， 而且混合加法和倍乘运算的总花费只需要5M+4S+5D.

本文主要研究形如Wa，b:y2=b2(a2- 4)x4- 2abx2+ 1 的Jacobi 四次曲线， 该类曲线在所有Jacobi 四次曲线中的比例接近二分之一， 且具有很好的密码学属性. 通过构造新的双有理等价变换， 本文得到了非常快速的差分加法和倍乘公式. 在射影w-坐标系统下， 混合加法和倍乘运算的总花费仅需要5M+4S+1D或者3M+6S+3D. 相较于Jacobi 四次曲线上的已有结果， 本文提出的公式是目前最有效的.

本文的组织结构如下， 第2 节回顾并总结了Jacobi 四次曲线的基本知识和差分加法公式的基本内容，第3 节研究了Wa，b曲线的一般性质， 第4 节构造快速的差分加法公式并给出快速算法. 最后第5 节总结全文并和以前的研究作简要的对比.

在整个文章中， 如果不加说明， 总是假定域K和有限域Fq的特征大于3.χ表示有限域Fq上的二次特征，u是有限域Fq上的平方元当且仅当χ(u)=1.

2 预备知识

2.1 Jacobi 四次曲线

设K是特征不等于2 的域.K上的Jacobi 四次曲线定义为

注意点(0，-1) 是一个2 阶点，Ed，a上没有其它的仿射二阶点. 退奇异性产生两个二阶无穷远点， 这两个点定义在K上当且仅当d是K上的平方元. 通过简单的代数运算可知， 2-y21+ax21=1-dx41， 且2-y21+ax21= 0 当且仅当[2]P是无穷远点. 使得[2]P是无穷远点的P是使得公式(1) 不成立的仅有的点， 因此公式(1) 不是完全的， 完全的含义是指公式对任意点都成立.

在射影坐标下， 单位元表示为(0 : 1 : 1). 点(X:Y:Z) 的逆是(-X:Y:Z). 在射影坐标下， 倍乘公式表示为[2](X1:Y1:Z1)=(X3:Y3:Z3)， 其中

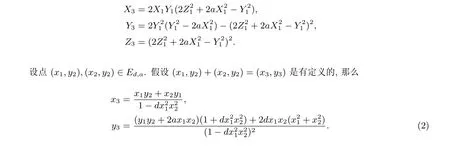
加法公式(2) 是统一的， 即它不要求两个点不一定不同， 但一般来说该公式不是完全的. 对任意的d，x1，x2∈K， 如果d是非平方元， 那么dx21x22/=1. 如果d是平方元， 但d(a2-d)/=0， 且点P=(x1，y1)和Q=(x2，y2) 是奇数阶点， 则dx21x22/=1. 关于更多的讨论公式的完全性的内容可见文献[6].

2.2 Differential addition

1987 年， Montgomery[9]提出了一个能抵抗边信道攻击的Montgomery 算法(见算法1). 在该算法的每一步都执行加法和倍乘运算， 因此可以认为在循环体中每一步循环所消耗的能量或计算时间都是无差异的， 因此可以抵抗简单能量分析攻击. 在Montgomery 算法中， 如果采用射影坐标， 则在中间的计算过程中只需要点的X和Z坐标， 而不需要Y坐标参与计算. 在算法结束时， 如果需要恢复Y坐标， 这可以通过公式由X和Z坐标计算得到.

算法1 Montgomery 算法Input: P ∈E(Fq)， k = ∑t-1 i=0 ki2i， where ki ∈{0，1}， kt-1 /= 0.Output: kP ∈E(Fq).1 P1 ←P，P2 ←2P;2 for i = t-2 down to 0 do 3 if ki = 0 then P2 ←P1 +P2， P1 ←2P1;5 end 6 else 4 P1 ←P1 +P2， P2 ←2P2;8 end 9 end 10 return P1 7

给定点P， 要计算[k]P. 在算法的主要执行过程中， 主要的中间参数是点P1和P2. 在初始化过程中，分别把P和2P赋给P1和P2. 迭代过程中，如果ki=0，把(2P1，P1+P2)赋给(P1，P2). 如果ki=1，把(P1+P2，2P2) 赋给(P1，P2). 算法最关键的地方在于， 任何时候总有关系式P2-P1=P成立. 这是该算法可以忽略掉Y坐标参与其中的关键. 当迭代结束时， 返回P1=[k]P. 例如， 计算[49]P=(110001)2P，得到链

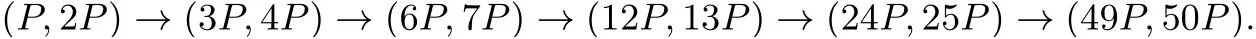
用x(P) 表示点P的x-坐标(在射影坐标系统下， 表示X和Z坐标对(X:Z)). 如果知道{x(P)，x(Q)，x(P+Q)，x(P-Q)}中的任意三个都可以确定第四个的值. 我们用xADD 和xDBL 表示Montgomery 算法中的差分加法和倍乘， 这个技巧称为Montgomery ladder， 算法2 展示了该过程， 该算法由x(P) 计算x([k]P). 最后的值x1=x([k]P). 最后的值x2可以用来恢复点[k]P的y-坐标.

算法2 Montgomery ladder Input: x(P) where P ∈E(Fq)， k = ∑t-1 i=0 ki2i with kt-1 /= 0.Output: x([k]P) ∈Fq.1 (x1，x2) ←(x(P)，xDBL([2]P);2 for i = t-2 down to 0 do 3 if ki = 0 then(x1，x2) ←(xDBL([2]P1)，xADD(P1 +P2));5 end 6 else 4(x1，x2) ←(xADD(P1 +P2)，xDBL([2]P2));8 end 9 end 10 return x1(and optionally x2 to recover [k]P from (P，x1，x2))7

3 Jacobi 四次曲线Wa，b 及其性质

本文主要考虑具有如下参数表示的Jacobi 四次曲线Wa，b， 其定义为在点(0，-1) 处是正则的. 点(0，1) 对应Montgomery 曲线上的无穷远点. 同理，φ-1在点(0，0) 处是正则的， 因为等价表示

由公式(3) 可知， 若b是一个平方元， 则Wa，b与Wa，1:y2=(a2-4)x4-2ax2+1 Fq-同构.

Jacobi 四次曲线Wa，b的j-不变量为256(a2-3)3/(a2-4). 因此，j(Wa，b)=0 当且仅当a2=3. 又3 是Fq中的平方元当且仅当q ≡1，11 (mod 12)， 因此， 若q不满足此条件则j-不变量不为0.j(Wa，b)=1728 当且仅当2a3= 9a， 即a= 0 或2 = (3/a)2. 2 是Fq中的平方元当且仅当(-1)(q2-1)/8= 1， 即q ≡±1 (mod 8). 作为密码学应用， 一般要求Jacobi 四次曲线满足j-不变量不等于0 和1728. 因此， 参数a应满足a2/=0，3，4，9/2.

熟知， 在有限域Fq上， 与一个给定的椭圆曲线E同构的椭圆曲线的个数为(q-1)/|Aut(E)|[13]， 由此， 以及上面的讨论可得如下引理.

引理3 给定Fq上一Jacobi 四次曲线Wa，b:y2=b2(a2-4)x4-2abx2+1. 则与它Fq-同构的椭圆曲线的个数为

在曲线Wa，b的两个参数a和b中，a基本上决定了曲线的几何属性. 假设a2/= 0，3，4，9/2. 由公式(3) 可知，Wa，b与Wa，¯b是Fq-同构的当且仅当存在u ∈F*q使得¯b=u2b. 同理， 取¯a=-a， 则Wa，b与W-a，¯b是Fq-同构的当且仅当存在u ∈F*q使得¯b=-u2b.

假设a2/=0，3，4，9/2，a2/=¯a2， 且Wa，b与W¯a，¯b是Fq-同构. 则由公式(3) 可得

因为Wa，b与W¯a，¯b同构， 所以¯a2/= 4. 上述关于¯a2的二次方程在Fq中有解， 因此(a2-4)2(a2-9)2+4(a2-4)(2a2-9)2= (a2-4)a2(a2-3)2为Fq中的平方元， 知a2-4 是Fq中的平方元. 同理¯a2-4 也是Fq中的平方元. 以上论述表明， 当j(Wa，b)/=0，1728 且a2-4 不是Fq中的平方元时， 则不存在¯a2/=a2的Jacobi 四次曲线W¯a，¯b与Wa，b同构. 这些为安全曲线选择提供了依据.

4 Jacobi 四次曲线Wa，b 上的差分加法公式

这节讨论推导Jacobi 四次曲线Wa，b上的点差分公式. 对Jacobi 四次曲线Wa，b上的点P=(x，y)，定义它的w-坐标为

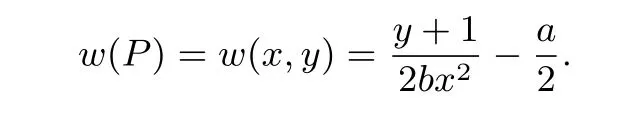
该函数对除了二阶点以外的所有仿射点都有定义. 在密码学应用上， 一般要求点的阶是奇数， 所以不影响其合理性. 双有理等价保持椭圆曲线间的点运算法则， 由引理1 和Montgomery 曲线的点差分公式，可以得到如下定理.

定理2 设P= (xP，yP) 和Q= (xQ，yQ) 是Wa，b上的点. 那么P，Q，P+Q和P-Q的w-坐标满足如下关系

由算法公式(5) 可知， 差分加法和倍乘的运算花费分别是3M+2S和2M+2S+1D， 所以总的混合射影w-坐标差分公式的计算代价是5M+4S+1D.

当域的乘法和倍乘计算的花费满足2M ＞3S时， 下述算法更有效， 它的混合射影w-坐标差分公式的计算代价是3M+7S+1D.

在上面的算法中， 差分加法和倍乘的的花费分别为3M+2S和4S+3D. 三个常数乘法中的两个常数乘法是被α乘， 另一个是被1/α乘.

5 总结

本文提出了一般Jacobi 四次曲线上的快速差分加法公式. 在射影坐标系统下， 本文提出的混合加法和倍乘运算的总花费只需要5M+4S+1D或者3M+6S+3D， 是目前Jacobi 四次曲线上最快的运算公式. 相比其他模型的椭圆曲线， 这也是最具竞争优势的记录. 文献[11] 中的差分加法公式， 使用(x2:Z2)坐标、混合加法和倍乘运算的总花费为5M+4S+5D， 比较可知本文的公式更有效. 结合Montgomery算法的差分加法公式在计算点乘方面非常有效， 而且能有效地抵抗简单能量分析. Jacobi 四次曲线相较于其它模型的椭圆曲线有很多的优势， 它上面的基本点加和倍乘运算非常高效， 本文构造的快速差分加法公式进一步增强了它在椭圆曲线模型选择中的竞争优势， 未来可进一步探索该类型椭圆曲线的有效算法和其它性质.