基于模格MLWR 的密钥封装方案优化与高效实现*

郝世迪， 孙冬旎， 梁志闯， 郑婕妤， 沈诗羽， 赵运磊

1. 复旦大学 计算机科学技术学院， 上海 200433

2. 复旦大学 软件学院， 上海 200433

1 引言

公钥密码学由Whitfield Diffie 与Martin Hellman 于1976 年首次提出[1]， 现已有各种基于不同困难问题的公钥密码体制. 目前应用广泛的公钥密码RSA (基于大整数分解问题) 和ECC (基于椭圆曲线离散对数问题)， 能被Shor 量子算法[2]在量子计算机上多项式时间内攻破. 为了应对量子计算的迅速发展， 能够抵抗量子攻击的密码—后量子密码成为国内外研究的热点.

基于标准格的方案中耗时的运算是有限域上的矩阵乘法， 而基于理想格和模格的方案中基础且耗时的运算是多项式的乘法. 数论变换(NTT) 因为其出色的拟线性复杂度O(nlogn)， 成为计算多项式乘法最高效的算法. 另外， NTT 在算法和实现上还有诸多的优点: (1) 计算向量-向量多项式乘法时能利用NTT的线性性减少逆向NTT 个数; (2) 用户存储多项式的NTT 的结果不需要额外的内存开销， 并能够多次使用多项式的NTT 结果; (3) NTT 能够进行即位运算(指的是一对数据经过一个蝴蝶操作的结果仍存放在原来这对数据的内存地址中)， 并利于高度向量化实现. 这些优点使得那些能够使用NTT 的方案的计算效率更优.

美国国家标准技术研究院(NIST) 于2016 年开始面向全球发起后量子密码标准化的算法征集工作，征集范围主要是PKE、KEM 和数字签名. 目前， NIST 公布了进入第三轮的15 个算法[5]， 其中， 七个决赛算法会作为通用算法， 未来得到更深入的研究和更广泛的应用; 此外还有八个算法作为备选， 可用来进一步优化提升或服务于具体的应用. 在七个候选决赛算法中有五个是基于格构造的. 其中基于MLWE 的Kyber[6]和基于MLWR 的Saber[7]被认为是非常有前途的KEM 方案. 特别地， Saber 其所有模数均为2 的方幂， 这带来以下优势: 避免使用较为复杂的拒绝采样; 不需要显式的模约减模块， 可直接通过移位操作完成模约减. 但是， 另外一方面， 其不是NTT 友好素数， 因此不能使用NTT 来加速多项式乘法.Saber 转向使用Karatsuba/Toom-Cook 算法， 但它们在实现效率方面明显劣于NTT. 然而， 近期工作[8]表明， 结合中国剩余定理(CRT)， Saber 也能使用NTT 计算多项式乘法， 进而提高其计算效率.

如今NIST 后量子密码标准算法竞赛已进行到了第三轮， 制定标准算法需要兼顾安全性、实现效率等性能. 而对格密码的研究虽然热度非常高但尚不成熟， 考虑到Saber 在NIST 后量子密码标准征集中的出色表现， 对其进行优化实现是十分重要的. 本文主要对Saber 进行优化， 提出了对Saber 进行改进的一种方案: 结合CRT， 选取最优参数对Saber 使用NTT 加速多项式乘法. 本文工作对后量子密码标准算法的优化和实际应用具有重要现实意义.

1.1 主要贡献

本文的主要贡献有以下3 个方面:

(1) 本文对Saber 提出一套新参数集， 相比原参数， 新参数集可以更好的平衡错误率、安全强度和通信带宽的关系.l= 2 时， 通信带宽节省了96 字节， 约6.8%， 量子安全强度由2107提高为2111;l= 3，4 时， 新参数可以在相近的安全强度下(172 对比170， 236 对比228)， 拥有更低的错误率(分别从2-136， 2-165降低为2-138， 2-187) 和更小的通信带宽(分别节省192 字节， 约9.2% 和64 字节， 约2.3%).

(2) 本文应用NTT 与CRT 结合的方式计算多项式乘法， 为了给该方案选定两个NTT 友好素数， 本文根据新参数(向量维数、多项式维度、模数和中心二项分布参数) 的具体取值， 并考虑到16 位之内的素数适合于NTT 的AVX2 实现， 最终选取NTT 友好素数为q1= 7681 和q2= 3329.选取这两个素数有如下几点好处: ①选取的素数3329 有利于正向NTT 使用延迟约减的策略; ②选取素数3329 能够降低本文方案私钥的尺寸; ③本文使用了跟Aigis-512/768 相同的模数7681，以及跟Kyber Round3 相同的模数3329， 这便于在软件实现上复用它们的代码， 硬件实现上共享它们的NTT 模块.

(3) 本文针对Saber 的新参数进行了AVX2 优化实现. 具体而言， 对算法中的约减模块、多项式运算模块、中心二项分布模块、私钥序列化模块、并行压缩模块以及并行编码/解码模块等进行AXV2优化实现. 实验结果表明， 本文在多项式乘法模块方面相比于Saber Round3 使用的Toom-Cook算法，算法性能平均提升约37%. 其中，向量与向量乘法的性能平均提升47%，矩阵与向量乘法平均提升27%. 另外， 本文的AVX2 优化实现相比于C 参考实现， 密钥生成算法性能提升约86%，密钥封装算法提升约88%， 密钥解封装算法提升约90%; 相比于Saber Round3 的AVX2 实现，密钥生成算法性能提升约21%， 密钥封装算法提升约23%， 密钥解封装算法提升约23%.

1.2 相关工作

在NIST 后量子密码标准化的算法征集第三轮中， Saber 是唯一的基于MLWR 的密钥封装方案.Saber 首先基于MLWR 困难问题构造一个IND-CPA 安全的公钥加密方案; 接着通过Fujisaki-Okamoto转换[9]得到IND-CCA 安全的密钥封装方案. Saber 使用Karatusba/Toom-Cook 计算多项式乘法. 现阶段对Saber 的优化主要分为两部分: 一是对多项式乘法的算法进行优化， 二是多平台的软硬件优化实现. 文献[10] 对Saber 使用了时间-内存平衡的Toom-Cook 算法. 文献[11] 将NTT 应用于Saber 的多项式乘法， 提升算法效率. 文献[12] 对Saber 使用AVX2 指令来并行批处理， 包括使用SHAKE-128 生成伪随机数， 使用SHA3 进行哈希以及多项式乘法三部分. 除此之外， 文献[13] 在ARM Cortex-M 上实现了Saber， 并在速度和内存占用方面进行了优化. 文献[14] 采用CRT 与NTT 结合的方式， 设计了可应用于Saber 的加速模块， 文中针对n= 256 的情况， 选取q1= 12289，q2= 13313，q3= 15361. 文献[15]提出了一种基于NTT 的快速多项式算法的通用硬件体系结构. 即便是Saber 参数均为二次幂， 也能直接应用NTT 通用组件， 无需更改硬件设计， 并且在此基础上提出了Saber 的首个掩码HW/SW 协同设计.

2 预备知识

本节主要介绍一些预备知识， 包括基本定义与符号表示、Saber 算法、数论变换以及AVX2 指令集.

2.1 基本定义与符号表示

2.2 Saber

Saber 是文献[7] 基于MLWR 设计的IND-CCA 安全的密钥封装方案. Saber 的构造分以下两步:第一步， 构造得到IND-CPA 安全的公钥加密方案(PKE); 第二步， 通过Fujisaki-Okamoto 转换[9]得到IND-CCA 安全的密钥封装方案(KEM). 为方便读者能够直观地理解， Saber 的IND-CPA 安全的公钥加密方案的伪代码见算法1-3， IND-CCA 安全的密钥封装方案KEM 详细伪代码见附录. 其中， gen 为某输出伪随机的扩展函数， 在Saber 中使用的是SHAKE-128.h1和h2是两个常数多项式:h1= 2ϵq-ϵp-1，h2= 2ϵp-2-2ϵp-ϵT-1+2ϵq-ϵp-1. 其模约减操作和乘等操作可直接通过移位来完成. 另外， 不需要拒绝采样生成A ∈Rl×lq. Saber 选择的参数如p，q均为2 的方幂， 详细参数见表1. 其中|pk|、|ct|、|B| 分别表示公钥长度、密文长度以及总带宽， 单位为字节，δ表示错误率， Classical Core-SVP 表示Core-SVP的经典安全强度， Quantum Core-SVP 表示Core-SVP 的量子安全强度.

表1 Saber 原参数表Table 1 Parameters of Saber

算法1 Saber.PKE.KeyGen Input: None Output: pk := (seedA，b)，s 1 seedA$←- {0，1}n 2 A = gen(seedA) ∈Rl×l q 3 s ←βl μ 4 b = ((ATs+h) mod q) ≫(ϵq -ϵp) ∈Rl×1 p 5 return (pk := (seedA，b)，s)

算法2 Saber.PKE.Enc Input: pk := (seedA，b)，m ∈R2 Output: c := (cm，b′)1 A = gen(seedA) ∈Rl×lq 2 s′ ←βl μ 3 b′ = ((As′ +h) mod q) ≫(ϵq -ϵp) ∈Rl×1p 4 v′ = bT(s′ mod p) ∈Rp 5 cm = (v′ +h1 -2ϵp-1m mod p) ≫(ϵp -ϵT) ∈RT 6 return c := (cm，b′)算法3 Saber.PKE.Dec Input: s，c = (cm，b′)Output: m′1 v = b′(sT mod p) ∈Rp 2 m′ = ((v-2ϵp-ϵT cm +h2) mod p) ≫(ϵp -1) ∈R2 3 return m′

2.3 数论变换

数论变换(NTT) 是离散傅立叶变换(DFT) 在有限域上的特殊情形. 标准的基于负折叠卷积[16，17]的n点NTT 需要参数满足q ≡1 (mod 2n)， 其中n是2 的方幂，q是素数. 正向NTT 为ˆf=NTT(f)，详细地:

Rq中多项式乘法h=fg ∈Rq能够通过h= INTT(NTT(f)°NTT(g)) 计算， 其中°表示点乘.FFT-trick[18]是计算NTT 的快速算法， 其复杂度为O(nlogn)， 而直接计算NTT 的复杂度为O(n2).由于ζn=-1 (modq)， 则有xn+1=(xn/2-ζn/2)(xn/2+ζn/2)， 正向FFT-trick 使用中国剩余定理表示为:

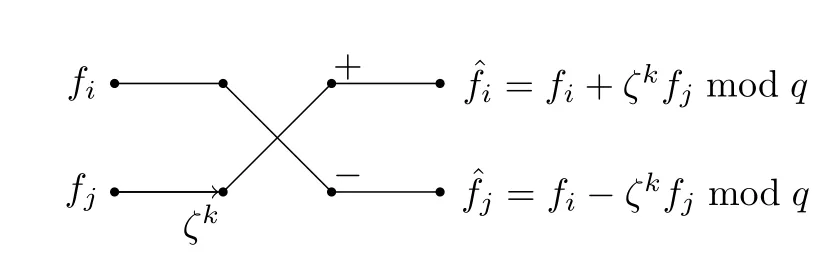
图1 Cooley-Turkey 蝴蝶Figure 1 Cooley-Turkey butterfly

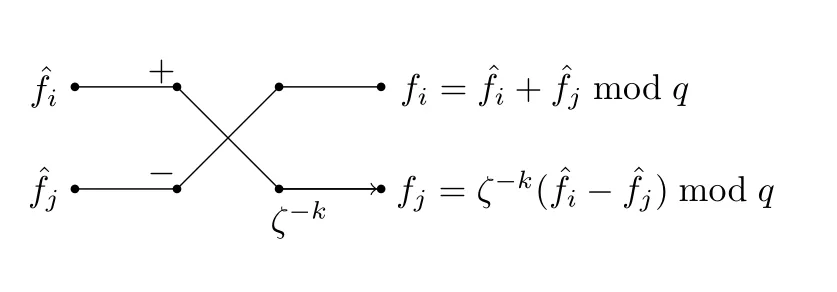
图2 Gentleman-Sande 蝴蝶Figure 2 Gentleman-Sande butterfly

FFT-trick 计算NTT 的伪代码见文献[19]. 完整的FFT-trick 过程能够表示为:

其中br(i) 表示无符号整数i的比特翻转值. 完整的FFT-trick 树形图表示见图3:

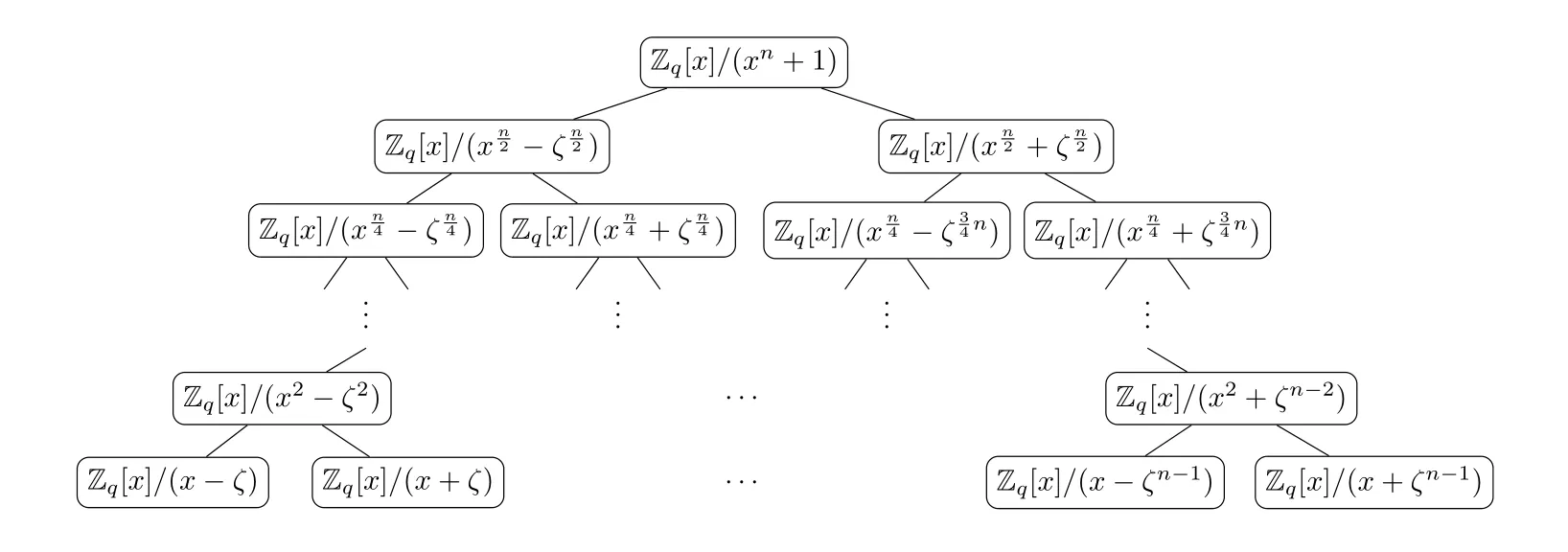
图3 完整的FFT-trick 树形图Figure 3 Complete FFT-trick tree diagram

FFT-trick 的计算过程并非必须进行到线性多项式项. 在文献[6] 中， 正向FFT-trick 只进行到:

得到NTT 域中的n/2 个线性多项式， 其中只需要Zq中n次本原单位根ω存在. 点乘是对应线性多项式的乘法. 然后再做逆向FFT-trick. 这种NTT 称为“不完整的NTT”[8]， 或者“裁剪的NTT”[20]， 它能弱化NTT 的参数限制条件到q ≡1 (modn). “裁剪NTT” 的FFT-trick 树形图见图4.

图4 “裁剪NTT” 的FFT-trick 树形图Figure 4 FFT-trick tree diagram of truncated NTT

其中，mi=(q1q2···qi-1)-1mod±qi.

文献[8] 利用这种方法计算Saber 的Rq中的多项式乘法h=fg ∈Rq， 因为Saber 的q不是NTT友好素数， 即q=2eq′+1 的形式， 无法在Rq中直接使用NTT. 简单来说， 文献[13] 考虑到Saber 中多项式的系数取值范围， 选取N=q1q2， 其中q1= 7681 和q2= 10 753 都是NTT 友好素数. 使用NTT分别计算f，g在Zqi[x]/(xn+1) 中的积， 再通过定理1 得到ZN[x]/(xn+1) 中的结果. 最后模q便得到f，g在Rq中的积.

2.4 AVX2 指令集

2008 年， 英特尔发布了高级矢量扩展(AVX) 指令集， 引入了256 位宽矢量指令. 这是对之前适用于128 位XMM 寄存器的SSE 指令集的改进. 除了从128 位宽度扩展到256 位宽度的SIMD 操作之外，AVX 还支持3、4 操作数， 且拥有更为宽松的内存对齐约束. AVX 在被称为ymm 的256 位SIMD 寄存器上运行， 分为两个128 位通道: 高通道和低通道. 大多数指令在“通道内” 工作， 即每个源元素仅应用于同一通道的其他元素， 不同通道不能互取数据.

AVX2 是2011 公布的AVX 的扩展， 它将多数128 位SIMD 整数指令扩展为256 位. AVX2 支持4路64 位整数加法、异或和向量移位[21]. AVX 由Sandy Bridge 微架构的英特尔处理器支持. 第一个商业化的处理器是2011 年1 月发布的的Core i7 和Core i5. 而AVX2 指令集是Intel 在2013 年的Haswell 22 nm 架构上首次引入的.

3 Saber 方案新参数选取与优化实现

3.1 方案算法描述及新参数选取

本文使用显式中国剩余定理(定理1) 和NTT 来计算Saber 中的多项式乘法， 其中， IND-CPA 安全的PKE 的伪代码见算法4-6， KEM 的伪代码见附录.

算法4 密钥生成算法PKE.KeyGen Input: None Output: pk := (seedA，b)，sk := (ˆs1，ˆs2)1 seedA$←- {0，1}n 2 A = gen(seedA) ∈Rl×l q 3 s ←βl μ 4 ˆs1 = NTT1(s)5 ˆs2 = NTT2(s)6 b1 = INTT1(NTT1(AT)° ˆs1)7 b2 = INTT2(NTT2(AT)° ˆs2)8 b = CRT(b1，b2)9 b = ((b+h) mod q) ≫(ϵq -ϵp) ∈Rl×1 p 10 return (pk := (seedA，b)，sk := (ˆs1，ˆs2))算法5 公钥加密算法PKE.Enc Input: pk := (seedA，b)，m ∈R2 Output: c := (cm，b′)1 A = gen(seedA) ∈Rl×l q 2 s′ ←βl μ 3 ˆs′1 = NTT1(s′)4 ˆs′2 = NTT2(s′)5 b′1 = INTT1(NTT1(A)° ˆs′1)6 b′2 = INTT2(NTT2(A)° ˆs′2)7 b′ = CRT(b′1，b′2)8 b′ = ((b′ +h) mod q) ≫(ϵq -ϵp) ∈Rl×1 p 9 v′1 = INTT1(NTT1(bT)° ˆs′1)10 v′2 = INTT2(NTT2(bT)° ˆs′2)11 v′ = CRT(v′1，v′2)12 cm = (v′ +h1 -2ϵp-1m mod p) ≫(ϵp -ϵT) ∈RT 13 return c := (cm，b′)算法6 解密算法PKE.Dec Input: s，c = (cm，b′)Output: m′1 v1 = INTT1(ˆsT1 °NTT1(b′))2 v2 = INTT2(ˆsT2 °NTT2(b′))3 v = CRT(v1，v2)4 m′ = ((v-2ϵp-ϵT cm +h2) mod p) ≫(ϵp -1) ∈R2 5 return m′

下文将对算法4-6 的具体细节进行解释. 算法4 和算法5 中的A ∈Rl×lq由gen(seedA) 生成， 其以seedA为种子通过SHAKE128 哈希函数产生随机比特串， 然后将每12 个比特拼接成一个系数. 该哈希函数每次只能产生168 个字节， 针对l= 2，3，4 的情况分别需要运行10 次， 21 次， 37 次才能产生相应长度的比特串.

算法4-6 使用的CRT() 函数， 将输入的两个多项式(向量) 的系数通过定理1 计算它们的中国剩余定理显式解. 如算法6 第3 行的v=CRT(v1，v2) 是将多项式v1和v2中对应分量上的系数通过定理1 计算得到v中对应分量的结果.

表2 给出了本文Saber 优化实现方案的参数选取. 本文对于LightSaber、Saber、FireSaber 三种情况， 使用统一的q=212=4096， 以及q1=7681，q2=3329.|pk|、|ct|、|B|分别表示公钥长度、密文长度以及总带宽， 单位为字节，δ表示错误率， Classical Core-SVP 表示Core-SVP 的经典安全强度， Quantum Core-SVP 表示Core-SVP 的量子安全强度. 其中， 错误率和安全强度的数据根据Saber Round3 提供的Sage 脚本测试得到.

表2 新参数表Table 2 New parameters for Saber

本文提出的新参数与原参数(见表1) 相比:q由213减小为212;p在l=2，3 的情况下， 由210减小为29;T在l=2，3，4 的情况下， 由23、24、26统一为24. 其中， 公钥长度|pk|=(lϵpn/8)+|seedA|， 故对于Saber、FireSaber 参数集， 新参数的公钥长度会减少ln/8， 即分别减少了64 字节、96 字节; 三组参数的密文长度|ct|=(lϵpn/8)+ϵT n/8 也分别减少了32 字节、96 字节、64 字节.

LightSaber 新参数与原参数相比， 通信带宽|B| =|pk|+|ct| 节省了96 字节， 约6.8%， 经典安全强度由2118提高为2122， 量子安全强度由2107提高为2111; Saber、FireSaber 新参数可以在相近的安全强度下(189 260 对比187 251)， 以更低的错误率(从2-136、2-165降低为2-138、2-187) 和更小的通信带宽(分别节省192 字节， 约9.2% 和64 字节， 约2.3%) 封装256 比特的密钥. 可以看到本文提出的LightSaber 新参数规模变小， 但安全强度提高了， 这是因为本文使用的Saber Round3 提供的Sage 脚本是基于文献[22] 提供的模拟器， 此模拟器测试(M)LWR 安全强度需要把其转换为(M)LWE 方式测试.其中， 影响安全强度的变量有向量维数和多项式维度的积(l*n)、模数q、秘密多项式的分布(参数为μ的中心二项分布) 以及噪音分布. 新参数表中减小了模数q和p的值， 噪音分布不变，l*n的值不变， 假如保持参数μ不变， 此时求解(M)LWR 问题会更加困难， 安全强度会变高， 但同时错误率也会变高. 所以本文减小了中心二项分布的参数μ， 以平衡安全强度和错误率. 以上分析表明本文提出的新参数可以更好地平衡安全强度、错误率和通信带宽的关系.

3.2 多项式的表示

在Saber 算法中， 多项式使用长度为n的数组来存储， 其中多项式的每一个系数的类型定义为无符号16 位整型. 本文的多项式系数使用[-q/2，q/2)∩Z 中的代表元来表示. 与采用无符号16 位整型相比，这样做的优势有以下两点: (1) 在进行系数相减操作时， 若出现负数结果， 则可直接存储， 不需要额外操作(如模q) 使其转换为正值. (2) 常见高效的模约减算法， 如Barrett 约减[23]和Montgomery[24]约减(详细伪代码见算法7 和算法8) ， 均作用于有符号整型. 这使得本文的方案能够使用以上高效模约减算法， 从而提升实现效率.

算法7 Barrett 约减Input: -β/2 ≤a ＜β/2， 0 ≤q ＜β/2 Output: r ≡a (mod q)，0 ≤r ≤q 1 v = ■2■log(q)」-1β/q■2 t = ■va/(2■log(q)」-1β)」3 t = tq mod β 4 r = a-t 5 return r算法8 朴素Montgomery 约减Input: -β/2 ≤a ＜β/2，-(q-1)/2 ≤b ≤(q-1)/2 Output: r ≡β-1ab (mod q)1 t0 = ■ab/β」 //得到a，b 乘积的高位2 v = ab mod β //得到a，b 乘积的低位3 v = vq-1 mod ±β 4 t = ■vq/β」5 r = t0 -t 6 return r

3.3 基于NTT 的方案改进优化

多项式乘法操作主要应用于矩阵-向量乘法和向量-向量乘法. 在此以向量-向量乘法为例来进行参数选择说明. 在Saber 中， 需要计算v=sTb， 其中s和b均为l维的多项式向量， 每个元素是n维的多项式. 利用NTT 的线性性，v能够通过下式计算:

其中，si系数取值范围为[-μ/2，μ/2]，bi系数取值范围为[-q/2，q/2)， 则v的系数在Z 上的取值范围为[-nqμl/4，nqμl/4]. 本文选取两个素数q1，q2使得在数值上满足q1q2＞nqμl/2. 除此之外， 还需考虑到:(1) 为了能够使用NTT，q1，q2需要是NTT 友好素数. (2) 为了方便使用AVX2 指令进行高效的并行计算，q1，q2需选择在16 比特以内. (3) 在满足前两点的基础上， 为了能够在存储数据时节省内存开销，q1，q2尽量小.

将表2 中对应的参数值n= 256，q= 4096， 以及三个参数集中μ，l的最大值μ= 4，l= 4 代入q1q2＞nqμl/2. 本文选择q1= 7681，q2= 3329. 可见，q1≡1 (mod 2n)， 可对模数7681 使用标准的NTT. 但由于3329 不满足256 点标准NTT 的参数条件， 只满足q2≡1 (modn)， 故本文对模数3329使用裁剪NTT. 具体而言， 本文使用256 点7 层的裁剪NTT， 点乘不再是对应数值的乘法， 而是对应线性多项式的乘法. 对模数7681 使用2n次本原单位根ζ= 62， 使用8 层的完整的NTT; 对模数3329 使用n次本原单位根ω=17， 使用7 层的裁剪的NTT.

图5 给出了以v=sTb为例， 使用CRT 与NTT 计算向量-向量乘法的详细过程. 需要说明的是，图中l ∈{2，3，4}，q= 4096，q1= 7681 以及q2= 3329. 对多项式向量进行正向NTT 和逆向NTT(INTT)、多项式向量之间的点乘和CRT 函数， 都跟4.1 节的介绍相同， 其中CRT 对输入v1和v2通过定理1 得到Rq1q2中的多项式.

图5 使用NTT 计算向量-向量乘法Figure 5 Compute vector-vector multiplication by using NTT

在此将详细分析选取q1=7681，q2=3329 这两个NTT 友好素数带来的三点好处:

(1) 本文选取的q2= 3329 有利于正向NTT 使用延迟约减的策略. 裁剪NTT 的正向NTT 共需要计算7 层. 在每一层的CT 蝴蝶操作中， 我们调用Montgomery 约减来计算系数和本原单位根的积， 而其输出的数值范围为(-q2，q2). 正向NTT 每计算一层， 多项式系数范围便扩大(-q2，q2).由于多项式系数初始范围为[-q2/2，q2/2)， 那么经过7 层的计算之后， 其输出的系数范围依然在有符号16 位整型可以表示的范围内， 且无数据溢出情况发生. 因此无需在正向NTT 过程中进行Barrett 约减， 而是在完成整个正向NTT 后才进行Barrett 约减. 这大大减少额外约减操作，提高算法实现效率.

(2) 在本文的Saber 优化实现方案中传输的私钥为(ˆs1，ˆs2)， 其中ˆs2的系数取值范围为[0，q2). 存储ˆs2的系数只需要12 比特. 相比文献[8] 选择的模数10 753， 本文选取的3329 能够降低私钥的尺寸， 减少私钥占用的存储空间. 对于LightSaber、Saber、FireSaber 三种情况(对应l=2，3，4)，私钥的尺寸分别能够减少128、192、256 字节.

(3) 7681 和3329 是基于理想格和模格方案常用的模数， 其中， 7681 是全国密码算法设计竞赛获奖算法Aigis[25]在Aigis-512/768 参数集下使用的模数， 而3329 是Kyber-Round3 使用的模数. 本文使用了跟它们相同的模数， 这便于在软硬件实现上进行代码复用. 详细来说， 在软件实现方面，本文使用模数7681 的NTT 时可复用Aigis-512/768 的代码， 使用模数3329 的NTT 时可参考Kyber-Round3 的代码; 在硬件实现方面， 本文方案能够跟Aigis-512/768 和Kyber-Round3共享NTT 模块或者直接移植它们的NTT 模块. 这同时能够为计算模块共享提供一致性模块接口， 也能够降低格密码落地化带来的经济成本. 另外， 本文方案若是使用经过安全验证的开源组件， 可避免出现意外漏洞.

本文方案除以上提到的在参数选取方面有创新外， 在采样以及加解密的实现中也有以下优化:

本文采用gen(seedA) 函数生成A， 对A分别做模数q1，q2的正向NTT 得到 ˆA1， ˆA2， 而不仿照Kyber-Round3 的做法， 直接从拒绝采样得到 ˆA1， ˆA2. 这是因为， 虽可节省2l2个正向NTT 操作， 但显然与本方案中 ˆA1， ˆA2需满足的 ˆA2=NTT2(INTT1( ˆA1)) 不符.

在参数选取的第(2) 点优势中提到， 本文方案是存储私钥s的NTT 形式ˆs1，ˆs2， 这样做可以节省2个正向NTT、2 个逆向NTT 和1 步CRT: (1) 密钥生成算法KeyGen 的行4 和行5 得到ˆs1和ˆs2后，不需要分别做逆向NTT 和CRT 得到s后再传输. (2) 解密算法Dec 中计算v=sTb′modp时， 可直接用ˆsT1，ˆsT2分别与ˆb′1，ˆb′2做点乘以及逆向NTT， 具体见Dec 的行1 和行2. 除此之外， 在加密算法Enc中， 行3 和行4 中对s′做正向NTT 得到ˆs′1，ˆs′2并存储后， 还可继续用于后续的向量内积， 具体见Enc的行5 和行6， 以及行9 和行10. 这样能够避免对s′重复做正向NTT.

3.4 AVX2 指令集对方案的优化实现

Saber 的AVX2 优化实现主要针对Saber 参考实现中耗时且可并行处理的功能模块进行优化加速，主要包含约减模块、多项式运算模块、中心二项分布模块、私钥序列化模块、并行压缩以及并行编码/解码模块.

3.4.1 约减模块

模块化约减是加速NTT 并行实现的核心. 在本文优化实现中， 模数一定时， 如果使用C 语言的“%”运算符来取模， 那么算法的时间不是恒定的， 会有遭受侧信道攻击的风险且效率较低. 为了安全且高效地实现算法， 本文参考文献[19] 中常数时间的约减算法， 即Barrett 约减和Montgomery 约减. 伪代码分别见算法7 和8. 其中β=216.

算法9 改进的Montgomery 约减Input: -β/2 ≤a ＜β/2，-(q-1)/2 ≤b ≤(q-1)/2，b′ = bq-1 mod β Output: r ≡β-1ab (mod q)1 t0 = ■ab/β」 //得到a，b 乘积的高位2 v = ab′ mod β 3 t = ■vq/β」4 r = t0 -t 5 return r

Barrett 约减算法[19]是将[-β/2，β/2) 上的a约减到[0，q] 中. 该算法采用预先计算的单字近似倒数v=/q」. 有了这个倒数， 当约减无符号的单字整数时， 就可以得到小于2q的代表元. 当素数q接近β/2 时， 就可以使用精度更高的单字倒数， 即v=2(q)」-1β/本文方案中， 在进行模数为q1=7681的NTT 时， 正向NTT 每计算一层， 输出系数的范围会扩大(-q1，q1)， 可计算出: 在第二层结束后系数范围已经超出16 位有符号整型可表示的范围， 此时需要对所有系数进行Barrett 约减; 同理， 在第五、第八层也需要进行Barrett 约减. 而在进行模数为q2=3329 的NTT 时， 正向NTT 每计算一层， 输出系数的范围会扩大(-q2，q2)， 可计算出七层正向NTT 之后， 系数范围仍可用有符号16 位整型来表示且无数据溢出， 故本文在模数为q2= 3329 的正向NTT 内部并没有使用Barrett 约减. 除此之外， 本文在私钥序列化模块使用Barrett 约减来使私钥的范围在[0，q1) 和[0，q2)， 保证后续计算的正确性， 减少了不必要的约减， 提高了效率.

Montgomery 约减算法是将a和b的乘积ab ∈(-βq/2，βq/2) 约减到(-q，q) 中. 算法并不是直接计算r ≡a(modq) 而是计算r′≡β-1a(modq). 在朴素的Montgomery 约减算法[19]中， 得到ab的高低位后， 需要对低位进行乘以q-1的运算. 而本文使用改进的Montgomery 约减算法[8]， 该算法的输入不仅有要做乘积的a和b， 还有预计算的b′=bq-1modβ. 这样做的好处在于可以省去朴素算法行3 中v乘q-1的乘法. 在本文方案中， 改进的Montgomery 约减用在蝴蝶操作中计算多项式系数和本原单位根ζ的积. 在本文的AVX2 优化实现中， 预计算表不仅存储ζ还存储了ζ ·q-1. 这样可以将朴素算法中系数先乘ζ再乘q-1的两个乘法转换为预计算的ζ·q-1与系数的一个乘法， 可节约一个乘法指令.

3.4.2 多项式运算模块

Saber 的多项式运算模块主要包含NTT 运算操作(正向NTT、逆向NTT、点乘)、多项式矩阵-向量乘法操作、多项式向量内积操作.

在AVX2 优化实现中， NTT 运算操作预计算表中ζ以及ζ·q-1的值都重复相应的次数， 使得并行载入时可以一次全部载入， 避免使用广播指令. 完整的正向NTT 划分为两部分: 对q1= 7681 正向NTT，共8 层， 分为第一层和第二到八层两部分; 对于q2= 3329 的正向NTT， 共7 层， 分为第一层和第二到七层两部分. 对于一个完整的正向NTT， 针对上述两部分分别设计一个函数来进行分层次调用. 在设计两个函数的时候， 要尽量充分利用AVX2 的寄存器， 设计一个正向NTT 第一层的函数最多可以用八个256ymm 寄存器， 去做128 个系数的蝴蝶操作(也就是64 对系数的正向NTT 第一层操作)， 因此第一层对所有系数做蝴蝶操作需要分两次进行. 在做完第一层之后， 计算结果被存回内存.

第二到七层/八层载入128 个系数， 在第一层的时候， 是间隔128 的一对系数进行蝴蝶操作， 而后面层数则可以对连续的128 个系数进行操作， 不需要额外的载入和存储系数， 只需要进行shuffle 重排系数顺序. 因此本文只使用了四次载入和存储就完成了256 个系数的正向NTT 操作， 减少了中间多次的载入和存储操作， 从而提高整体速度.

3.4.3 中心二项分布模块

在本文方案中， 私钥s的每一个系数均由中心二项分布算法来生成. 本文针对μ= 2 的情况， 对中心二项分布算法进行了AVX2 的优化实现， 细节见算法10. 该算法每次输入一个256 位的比特串buf， 得到私钥s的64 个系数. 算法需要先从buf 数组中取两组两比特来生成一个系数， 而使用AVX2 指令的操作数数据类型至少为8 位有符号整数， 此时以8 比特为一组直接进行运算会与预期结果有位置上的不同， 所以该运算结束后需要对其结果进行位置调整.

算法10 中心二项分布生成私钥AVX2 实现Input: 字节数组buf Output: 多项式r 的64 个系数1 vpbroadcastd (a，b，c)2 vmovdqu v0 ← buf[i]3 vpsrld v1 ← v0 ≫ 1 4 vpand (v0，v1)← (a & v0，a & v1)5 vpaddd v0 ← v0+v1 6 vpsrld v1 ← v0 ≫ 2 7 vpand (v0，v1)← (b & v0，b & v1)8 vpsrld (v2，v3)← (v0，v1) ≫ 4 9 vpand (v0，v1，v2，v3)← (c & v0，c & v1，c & v2，c & v3)10 vpsubb (v1，v3)← (v0-v1，v2-v3)11 vpmovsxbw (v0，v1，v2，v3)← (v1，v3)12 vpunpcklwd (v0，v1)← ((v0，v2)low，(v1，v3)low)13 vpunpckhwd (v2，v3)← ((v0，v2)high，(v1，v3)high)14 vmovdqa (v0，v1，v2，v3)

3.4.4 私钥序列化模块

私钥包括ˆs1和ˆs2. 由于AVX2 实现的正向NTT 采用延迟约减策略， 因此产生私钥的系数范围不一定在[0，q1) 和[0，q2). 为了正常进行私钥序列化操作， 对ˆs1和ˆs2的系数在序列化之前做了一次额外的约减， 使得其范围在[0，q1) 和[0，q2). 此处采用Barrett 约减(伪代码见算法7) 并行处理16 个系数. 由于AVX2 向量寄存器个数有限， 故本文一次性使用8 个ymm 寄存器做128 个系数的约减， 分两次完成对所有系数的约减.

3.4.5 并行压缩模块

在KeyGen 和Enc 过程中都存在对多项式的压缩过程以节省带宽(见算法4 第9 行和算法5 第8行). 这个过程中有p/q和向下取整的运算. 由于本文方案的参数均为2 的方幂， 因此除法和向下取整可以用移位操作来实现， 即=x ≫(ϵq-ϵp). 除此之外， 此过程可以用AVX2 实现并行优化. 首先将要做压缩的多项式系数载入一个256 位的AVX2 寄存器中， 这样一个寄存器可以存放16 个系数， 此时就可以对其一次性完成算法11 的压缩运算， 对于多项式向量中的一个多项式， 只要做16 次运算就可以完成该多项式所有系数的压缩过程. 最后将最终结果存回之前的变量位置.

算法11 压缩过程的AVX2 实现Input: 多项式b Output: 每个系数被压缩至ϵp 比特后的b 1 vpaddw b ←b+h1 2 vpsraw b ←b ≫(ϵq -ϵp)

3.4.6 并行编码/解码

算法5 行12 和算法6 行4 分别被称为编码和解码过程， 这里以编码过程为例来进行描述: 编码算法的输入为明文m， 以及多项式v′. 其中明文m为256 位的比特串， 算法需要对其每一位分别进行编码操作， 此过程可以用AVX2 实现并行优化(详细见算法12). 首先要一次性取出明文m中的16 位， 而后与v′的16 个系数并行完成后续操作， 所以对于明文m， 只需要做16 次运算便可以完成编码.

算法12 编码过程AVX2 实现Input: 明文m， 多项式v′Output: 密文cm 1 vpand m ←m & 1 2 vpsllw m ←m ≪ϵp -1 3 vpand m ←m & {1}ϵp 4 vpaddw v′ ←v′ +h1 5 vpsubw cm ←v′ -m 6 vpsrlw cm ←cm ≫(ϵp -ϵT)

算法13 解码过程的AVX2 实现Input: 密文cm， 多项式v Output: 解密明文m′1 vpand cm ←cm & {1}T 2 vpsllw cm ←cm ≪(ϵp -ϵT)3 vpaddw v ←v+h2 4 vpsubw cm ←v-cm 5 vpand cm ←cm & {1}ϵp 6 vpsrlw m′ ←cm ≫(ϵp -1)

3.5 恒定时间实现

计时攻击[26]是一种常见的侧信道攻击. 它指的是攻击者能够根据密码方案在软件或硬件中的执行时间信息来推断出所执行的运算操作， 甚至能够推算出该操作所涉及的一些秘密信息， 如私钥. 针对计时攻击最简单的对策是确保实现的执行时间独立于所处理的秘密数据. 目前来说， NIST Round 3 中的方案实现均考虑了计时攻击， 并采用了恒定时间(constant-time) 实现策略. 因此， 本文的优化实现方案采用了以下的恒定时间实现策略. 对于方案中涉及到模约减的地方， 如NTT 运算中的modq1和modq2， 本文使用Barrett 约减和Montgomery 约减， 而并没使用“%” 运算符. 这是因为“%” 运算符的执行时间与输入数据长度密切相关. 而Barrett 约减和Montgomery 约减均是恒定时间实现， 能够大大降低泄露秘密数据的风险. 由于AVX2 指令集缺乏与“%” 运算符有关的指令， 而Barrett 约减和Montgomery 约减仅使用到加减乘法和移位， 使用Barrett 约减和Montgomery 约减更利于AVX2 实现. 对于本文中的生成公钥A的gen 函数， 由于模数q为212，A的每一个系数均可以直接由12 个随机比特拼接得到， 而无需使用拒绝采样. 因为q是固定的， 所以生成A的时间是恒定的. 这区别于Kyber 生成A的执行时间与拒绝概率有关. 针对生成秘密多项式s和s′的中心二项分布模块， 它使用μ个比特生成一个系数. 它生成s和s′的时间明显也是恒定的. 针对压缩模块， 与Saber 原来的实现方式[7]一样， 本文使用移位(即x ≫(ϵq-ϵp)) 来处理每一个系数， 移位的执行时间也独立于被操作数x.

4 性能测试与比较

本节给出了Saber 优化方案的C 参考实现和AVX2 优化实现的性能测试数据. 本文进行的性能测试都是在关闭Hyper Threading 和Turbo Boost 的情况下， 硬件运行环境为2.30 GHz 的8 核Intel Core i7-10510U 处理器， 16 GB 的内存， 软件运行环境为Ubuntu 20.04.1 操作系统， 编译器为gcc 9.3.0， AVX2优化实现的编译选项为-Wall -Wextra -O3 -fomit-frame-pointer -msse2avx -mavx2 -march=native -lcrypto. C 参考实现的编译选项为-Wall -Wextra -Wmissing-prototypes -Wredundant-decls -O3 -fomitframe-pointer-march=native. 本文使用CPU 周期来衡量各算法的效率，故运行密钥生成算法KeyGen，密钥封装算法Encaps 和密钥解封装算法Decaps 10 000 次， 取其平均值.

4.1 多项式乘法部分性能对比

图6 给出本文提出的Saber 优化实现方案，与Saber Round3 和文献[8]中向量-向量乘法以及矩阵-向量乘法操作的对比. 由图中测试结果显示， 多项式乘法部分采用NTT 与CRT 结合的方式， 借助AVX2指令集的单指令多数据的特性， 可最大化增加并行处理的数据量， 从而比文献[8] 的性能平均提升26%， 其中向量与向量乘法部分性能平均提升40%， 矩阵与向量乘法部分平均提升11%; 与Saber Round3 相比，向量与向量乘法部分性能平均提升47%， 矩阵与向量乘法部分平均提升27%.

图6 多项式乘法的性能对比Figure 6 Performance comparisons of polynomial multiplication

4.2 本文方案参考实现与优化实现的性能对比

图7 给出本文提出的Saber 优化实现方案的AVX2 优化实现与参考实现的对比. 由图中测试结果显示， 密钥生成算法比参考实现提升约86%， 密钥封装算法比参考实现提升约88%， 密钥解封装算法比参考实现提升约90%.

图7 参考实现与优化实现的性能对比Figure 7 Performance comparisons of reference and optimized implementation

4.3 本文方案与Saber Round3 优化实现的性能对比

图8 给出本文提出的Saber 优化实现方案， 与同类算法方案Saber Round3 的AVX2 优化实现的对比. 由图中测试结果显示， 相比于Saber Round3 的AVX2 实现， 密钥生成算法性能提升约21%， 密钥封装算法提升约23%， 密钥解封装算法提升约23%.

图8 优化实现的性能对比Figure 8 Performance comparisons of optimized implementation

结果显示， 本文方案在实现效率上有很大的提升. 在Saber Round3 中， 使用Karuatsuba/Toom-Cook 算法来进行多项式乘法， 而本文结合CRT， 选取更优的参数对Saber 使用复杂度更低、更利于高度向量化实现的NTT 进行加速， 使得本文方案的计算效率更优. 除此之外， 本文选取的NTT 友好素数与文献[8] 选取的素数相比， 使得本文方案有更小的私钥长度以及更少的约减操作， 达到计算效率上的最优.