疲劳统计学智能化的进一步研究

徐家进，高镇同

1.力中国际融资租赁有限公司,广州 510620 2.北京航天航空大学 航空科学与工程学院,北京 100083

《疲劳统计学智能化中的高镇同法》中指出，威布尔分布是一种全态分布，即不仅可描写左偏、右偏的数据，在一定程度上也可描写对称的数据。在这个意义上比高斯分布用途更为广泛，特别是在拟合结构的疲劳寿命方面起到非常重要的作用。但因在确定威布尔分布3参数方面遇到了困难，因此人们往往将“最小寿命”归零。但这种做法是不合适的，因为“最小寿命”的物理意义是可靠度为100%的寿命，应该称为“安全寿命”，这是非常重要的。为了确定威布尔分布的3个参数，以往采取图解法和解析法，前者使用不便，且误差比较大；后者则是要解3个联立的超越方程组，尽管可用计算机来解，但有时候会出现解出的安全寿命这个参数会大于实际数据的最小值，即会存在这种不自冾的问题。文献[1]中利用最小二乘法和Python特点提出了高镇同法，比较好地解决了这个问题。这是疲劳统计学智能化的开始。而在本文则是更进一步，只要给出(疲劳寿命)样本数据通过计算机就可自动判断该数据的总体服从的最佳分布(正态分布或威布尔分布)，并同时给出该分布的参数。同时智能化地给出每一个疲劳寿命的置信区间。恰恰是疲劳统计学智能化的一种成果。

尽管解析法有时候会出现不自冾的问题，但在实际应用中并非一定会出现不自冾问题。此时用高镇同法也会得到一组威布尔分布3个参数的估计值，而与解析法得到的一组估计的参数值是不相同的。于是产生了到底采取哪一组参数更加合适的问题。这就需要给出一个所谓“优劣”的标准。注意到高镇同法的本质就是要选择适当的安全寿命参数使得得到的威布尔分布与“理想”的可靠度的相关系数最大。故可用相关系数绝对值的大小作为衡量标准是恰当的。但不难看出相关系数可在线性拟合中起作用，遇到非线性拟合时就必须要用决定系数大小来作为标准。这个标准也可作为衡量各算法结果“优劣”的标准。进一步还需研究各参数的“置信区间”问题。但研究表明，同时给出这3个参数的置信区间是有困难的。因此，本文不仅给出了解决拟合“优劣”的标准问题，同时也给出了威布尔分布在某种可靠度下每一点(即疲劳寿命)的置信区间的一个智能化解决方案，而这恰恰也是人们在实际工作中最需要的。

1 相关系数和决定系数

一般情况下此文说到相关系数都是指皮尔逊相关系数(Pearson Correlation Coefficient)，若、为2个随机变量，则它们的相关系数为

=Cov(,)(Var()Var())12

(1)

式中：Var()、Var()分别为和的方差;Cov(,)是协方差[(-())(-())]，(·)为期望。

由柯西不等式：

(2)

式中：、分别表示和的第个分量。若将和看成为2个矢量，那么它们的所谓相关系数实际上就是这2个矢量的夹角余弦，这就是相关系数的几何意义。为零表明2者成90°(正交)，因此完全不相关。反过来||越大则2者的夹角越小因此越相关，=+1称之为完全正相关,而=-1完全负相关。

相关系数在统计学中有着非常重要的地位，是衡量2个变量线性相关密切程度的指标，与此有关的另外一个指标就是决定系数。注意到数据由某曲线拟合的程度可定义为

1-SSE/SST=1-Var(-)Var()

(3)

=+

(4)

式中：、分别为斜率和截距，由此可得

=

(4a)

=-

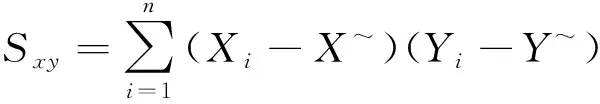
(4b)

因

(5a)

但由式(4)和式(4b)可得

-=(-)

(5b)

故有

-=(-)-(-)

(-)

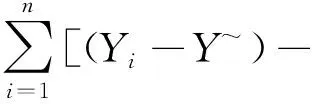
(6)

注意到式(4a)中的定义可知式(6)=0，

(7)

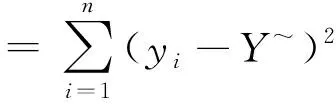
=SSR/SST

(8)

由式(5b),

=[()]=

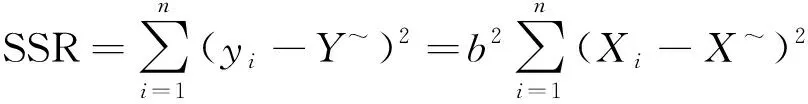
注意，式(1)可改写为=()12。

不难看出，的范围是[0,1],而的范围是[-1,1]。另外的统计意义是拟合程度，也可理解为变量对变量的解释程度(回归误差和)的大小。由此可见，决定系数这个概念的意义更加广泛，只不过在线性拟合的情况下

=

(9)

在非线性拟合情况下所谓相关系数就没有意义，决定拟合程度只能用决定系数来判断，且只能用式(3) 这个定义式。

事实上在比较各种分布拟合数据的过程中会发现不同的“参照系”会得到不同的决定系数。比如用高镇同法为了求出威布尔分布的位置参数先要确定与数据“理想可靠度”最大的决定系数(因为此时是线性拟合，因此仍然可用相关系数)。然后再由最小二乘法定出威布尔分布的其他2个参数(形状参数和尺度参数)。但要与解析法及高斯分布比较究竟哪一个方法拟合得更好呢？就得将这3种方法得到的拟合可靠度曲线和理想可靠度来比较。此时就不再是线性拟合的情况下，就不能再使用相关系数而必须要用决定系数了。

2 以理想可靠度作为基准的决定系数

所谓“理想可靠度”，实际上是指“可靠度估计量”：

=1-(+1)

(10)

式中：为第个疲劳寿命的可靠度;为疲劳寿命总个数。

为什么称之为“理想”可靠度？这是因为式(10)对于任何分布都是适用的，因此提供了一个参照标准。实际上高镇同法的基础也是建立在与理想可靠度的相关性之上的，即以此为标准来选择位置参数。不过此时用的是对数空间中的相关系数，即ln(ln(-1/))与ln(-)的相关系数。而不是直接拿与威布尔分布的可靠度[exp(-(-)/)]的决定系数来比较(、、分别为威布尔分布的位置、尺度和形状参数)。

用文献[2]第136页的疲劳寿命数据来说明这个问题。利用Python代码，运行后可得

={350, 380, 400, 430, 450, 470, 480, 500, 520, 540, 550, 570, 600, 610, 630, 650, 670, 730, 770, 840}，表示疲劳寿命数组，该数组的长度LS= 20， 疲劳寿命均值= 557.0， 标准差= 132.15， 中值= 545.0, 偏态系数=0.408。

用高镇同法结果：= 2.040，= 320.98，= 276.60,= 0.999 218，= 0.605，,、,分别为相应最大相关系数的形状参数、长度参数及安全寿命(位置参数) 和相关系数。与理想的可靠度的决定系数来比较：高镇同法计算的威布尔分布的决定系数=0.998 24，高斯分布的决定系数=0.989 48，用解析法计算：=2.211,=312.32，=280.39，=0.503，用解析法计算的威布尔分布的决定系数=0.995 86。

由此可见，解析法和高镇同法得到的结果与理想可靠度的决定系数结果相差无几，这从它们得到的3个参数相差“不大”也是可预料得到的。这也说明数据拟合并没有一个绝对正确的答案。高斯分布与理想可靠度相应的决定系数也是非常接近1的，尽管比威布尔分布相应的决定系数要小一些。同时可注意一下偏态系数，原始数据的偏态系数为0.408，而用高镇同法和解析法得到的偏态系数分别为0.605和0.503。尽管解析法得到的偏态系数与原始的偏态系数更加接近一点，但决定系数却小了一点，若以决定系数为标准则应取高镇同法的结果。

至于文献[1]中例2已经表明解析法无法计算出不自冾的结果，但高镇同法是可解的，且高镇同法得到的相关系数要比高斯分布要大，故可采用高镇同法的结果,看起来高镇同法的结果更佳。但并没有给出严格的论证，故要对威布尔分布要做进一步的研究。

3 利用数据分组对威布尔分布做进一步的研究

如何才能对威布尔分布做进一步研究呢？考虑到样本容量比较大的时候往往会对其分组，其实通常做统计分析时也常常需要就数据分组。数据分组的好处是将“大数据”变成为好处理的“小数据”，又能保留原来“大数据”的“最主要”的特性。不过为此是要付出代价的，代价之一是分组是有讲究的，是需要人为“干预”的。另一个代价则是无论怎样分组多多少少都会“扭曲原意”， 尽管如此分组不失为一个统计分析的方法。比如在文献[2]第253页介绍卡方检验时就将在同一应力水平下测得的100个试件的疲劳寿命成为9组，再根据9组中不够10次的“组”进行必要的“合并”成为了6组，然后再进行卡方检验。结果表明这组数据是不符合高斯分布的。那么属于什么分布呢？是不是符合威布尔分布呢？这就需要进一步研究。其实这也是发现高镇同法的一个契机，这一点在文献[1]中已经披露了。只不过当时没有将此数据进行分组而是直接利用高镇同法对其进行计算。

为了更加直观地感受不同方法不同分布对于数据的拟合程度，修改Python代码后得如下结果：

={3.08, 3.26, 3.32, 3.48, 3.49, 3.56, 3.69, 3.7, 3.78, 3.79, 3.8, 3.87, 3.95, 4.07, 4.08, 4.1, 4.12, 4.2, 4.24, 4.25, 4.28, 4.31, 4.31, 4.36, 4.54, 4.58, 4.6, 4.62, 4.63, 4.65, 4.67, 4.67, 4.72, 4.73, 4.75, 4.77, 4.8, 4.82, 4.84, 4.9, 4.92, 4.93, 4.95, 4.96, 4.98, 4.99, 5.02, 5.03, 5.06, 5.08, 5.06, 5.1, 5.12, 5.15, 5.18, 5.2, 5.22, 5.38, 5.41, 5.46, 5.47, 5.53, 5.56, 5.6, 5.61, 5.63, 5.64, 5.65, 5.68, 5.69, 5.73, 5.82, 5.86, 5.91, 5.94, 5.95, 5.99, 6.04, 6.08, 6.13, 6.16, 6.19, 6.21, 6.26, 6.32, 6.33, 6.36, 6.41, 6.46, 6.81, 7.0, 7.35, 7.82, 7.88, 7.96, 8.31, 8.45, 8.47, 8.79, 9.87}，数据未分组结果：= 5.32，= 1.29，=5.07，= 1.021。数据分组结果：= 6.79，= 2.09，= 6.77，=0.043， 每组上限:3.84，4.68，5.52，6.35，7.19，8.03，8.87，9.87，每组含有的个数:11，21，29，25，5，4，4，1，累积频率:0.999，0.89，0.68，0.39，0.14，0.09，0.05，0.01。

对分组高镇同法：=1.948，=2.73，=3.76,=0.999 247，=0.666，对分组用解析法：估计=3.253，估计=4.26，估计=1.50，=0.091。 与分组得到的实际积累频率的决定系数：由高镇同法得到的决定系数=0.994 82，由解析法得到的决定系数=0.955 84，由高斯分布得到的决定系数=0.957 46。不分组高镇同法：=2.147，=2.87，=2.78,=0.993 763，=0.539。与不分组的可靠度的决定系数：由高镇同法得到的决定系数=0.989 03，由高斯分布得到的决定系数=0.979 11。

由上述计算结果可得出如下几个看法：

1) 原来用解析法得出最低寿命会大于实际数据中的开始3个数据，这显然是不符合“安全寿命”这个概念的(即不自冾)。而现在将这100个数据分成为8组后，这个问题表面上是不存在了。但图1表明用解析法得到的结果与高斯分布几乎到了不可分辨的地步，而且明显偏离了实际数据，故解析法和高斯分布这2个方法都不可取。

2) 从图1及相关系数都可发现，对于分组数据高镇同法得到的3参数威布尔分布的拟合曲线都比用解析法得到的3参数威布尔分布及高斯分布拟合得要好。尽管如此，由高镇同法得出的安全寿命仍然明显大于原始疲劳寿命数据中的最小值。因此在这个意义上分组并不是一个好主意。

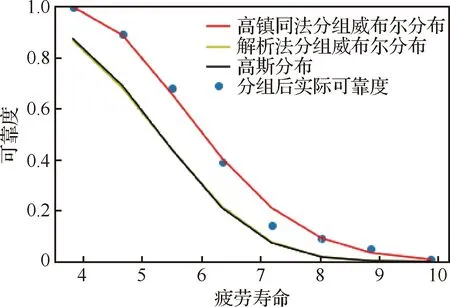
图1 数据分组的各种分布与实际可靠度拟合情况Fig.1 Fitting of various distributions and ideal reliability of data grouping

3) 再回到不分组的情况。从曲线拟合图(图2只给出了20个数据而不是100个数据点，主要原因是后者的图太密，以致看不清)，用高镇同法计算出来的3参数威布尔分布与高斯分布也是区别“不大”的，很难说哪一条更好。也只能从决定系数这个角度去看，此时可确定用高镇同法计算出来的3参数威布尔分布比高斯分布是略胜一筹的。而且从偏态系数这个角度看，原数据偏态系数是相当大的，故用高斯分布来拟合确实是不合适的。即偏态系数可作为判断是否符合高斯分布的一个重要的考虑因数。

图2 未分组数据的各种分布与理想可靠度拟合情况Fig.2 Fitting of various distribution and ideal reliability of data ungrouping

4) 将相同数据用不同的分布或不同的算法得到拟合曲线与相应的可靠度的决定系数的大小作为拟合好坏的标准还是可行的。如果用3参数威布尔分布拟合比高斯分布拟合更好的话，那么高斯分布作为一阶近似是有道理的。这也是为什么即使是疲劳寿命的数据有时候用高斯分布来拟合也会得到似乎不错的结果的原因。

4 威布尔分布的置信区间：方法1

第3节讨论了用什么标准来判别样本数据用什么分布比较合适或用什么算法得到的参数更加合适的问题。事实上数据是客观的，如何去描述是存在主观意图的，即从某个角度去看这些数据，以便人们理解和利用这些数据。以往各种统计检验大都是以高斯分布为基础，如比较著名的t检验尽管可以不知道总体的标准差，但仍然是建立在总体分布是高斯分布的基础之上。所谓置信区间也是如此，更加重要的是置信区间仅仅是针对高斯分布的2个参数而言的，而且往往是需要已知其中一个求出另外一个。问题是对于威布尔分布来说如何求它的置信区间似乎成了一个新问题，特别是需要知道各种不同可靠度之下“寿命估计”，而这种寿命估计也是需要一个“置信区间”的。

那么如何求威布尔分布的置信区间呢？自然先想到的是求威布尔分布参数的置信区间。但同时求出3个参数的置信区间是相当困难的，通过下面的论述将理解这一点，为此要从最小二乘法说起。事实上，从文献[1]中推出高镇同法时指出3参数威布尔分布的可靠度为

=1-()=exp{-[(-)]}

(11)

式中:表示可靠度为的疲劳寿命。于是式(11)在取2次自然对数后可得

ln(ln(1))=ln()-ln()

(12)

式中：=1-/(+1)

再设

=ln(ln(1/)),=ln(-)

(13)

=+

(14)

式中：

=-ln()，=exp(-)

(15)

故可由计算机直接通过最小二乘法求出使得与的相关系数最大的，以及相应的和的估计值和，与此同时也就求出的估计值了，这就是高镇同法。现在的问题是数据是在什么程度上服从威布尔分布，尽管通过相关系数可认为该数据与高斯分布相比威布尔分布更合适。但并没有给出在一定的置信度下该数据的分布是否符合威布尔分布的统计检验。

注意到此时的回归线性方程式(14)的2个待定系数与(就是威布尔分布的形状系数，而通过及也马上可得威布尔分布的尺度系数)是通过回归误差平方最小化来确定的，服从(0,)分布

=-(+)

(16)

为此可先讨论关于、及的估计问题。首先要证明由最小二乘法得到的和是最优线性无偏估计量。按最小二乘法

=

(17)

=-

(18)

式中：

(19)

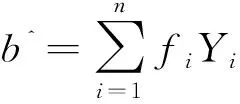
(20)

式中：=(-)，同时注意到

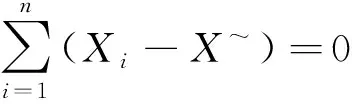
(21)

这就证明了的线性性。不难证明

(21a)

又因式(18)容易证明也是的线性函数,则

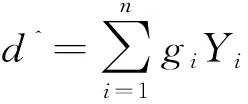
(22)

式中：

=(1-)

(22a)

再注意到式(16)和式(20)，

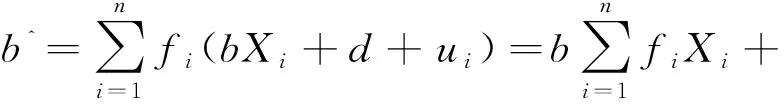
(23)

在此要注意利用了式(21)和式(21a)。

又因式 (16) 和式(22)可得

(24)

在此要注意到式(22a)

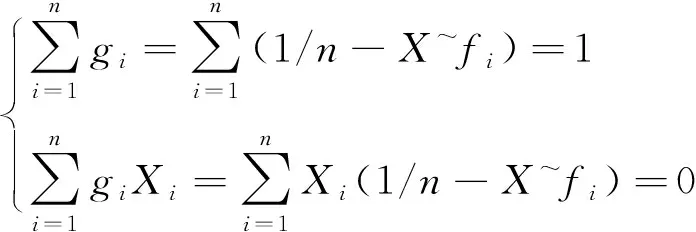
(24a)

由此来证明参数和的无偏性，即要证明

()=,()=

(25)

事实上，由式(23)可得

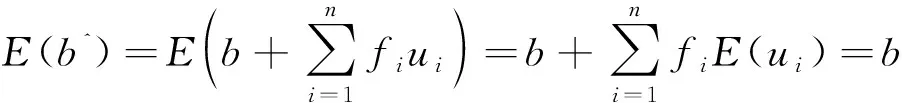
同理可证明()=。

现进一步来求的方差

(26)

而

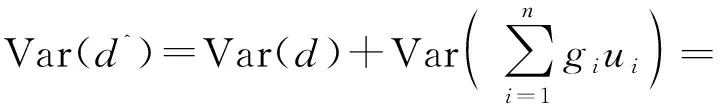
(26a)

在此要注意

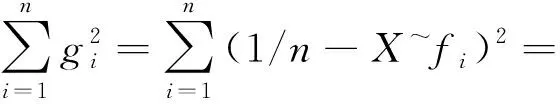
1+=()

(26b)

不过至此问题还没有完全解决，因为误差方差其实是未知的，因此需要通过可观察数据对其进行估计。注意到可观察的误差为

(+)=+(-)+-

(27)

注意到，和的均值都为零

(28)

即可得

(29)

按照假定，

(30)

注意到与的相互独立性可得

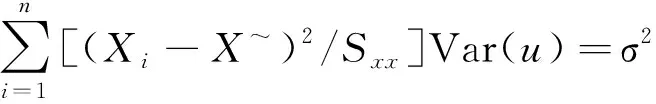
(30a)

(^)=(-1)+-2=(-2)

(30b)

的无偏估计为

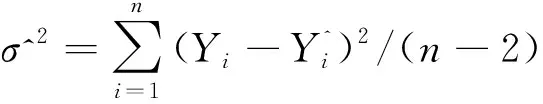
(31)

这与文献[4,10]得到的结果一致。

于是威布尔分布的在置信度=1-(为显著度)的条件下是否显著以及威布尔参数本身的估计了。从形状参数开始。注意到的估计值是服从高斯分布(,), 其中可由无偏估计的=/(-2)来代之。

由此可得

=(-)～(-2)

(32)

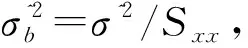
1) 零假设，=0(意味着在显著性水平之下威布尔分布是不正确的)。

2) 备择假设，≠0(意味着在显著性水平之下威布尔分布是正确的)。

||≤2(-2)

(33)

时接受零假设，否则接受备择假设。

至于的置信区间就比较容易确定了。此时用1-来代表置信水平(置信度)，那么又由式(32)可得的置信区间为

(34)

同理可得关于的置信区间，不过此时，

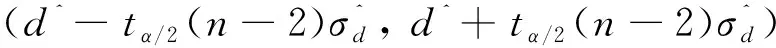
(35)

注意到式(15)的=-ln()→=exp(-)。 因此的置信区间为

(36)

于是λ的置信区间为

exp{[-+2(-2)^]})

(37)

式中

(38)

下面用具体例子来说明。顺便指出在此没有用文献[4]中的数据，是因为无法验证其所得到的结果，这确实是很遗憾的事情。

还是利用文献[2]第136页中的数据:{350,380,400,430,450,470,480,500,520,540,550,570,600,610,630,650,670,730,770,840}×10循环。均值=557，标准差=132.15，中值=545。

同样可利用Python代码得到如下结果：=276.6，=0.999 22，=2.040，=-11.77，=320.98，=0.05,=107.18>_=2.10，则该分布的总体符合威布尔分布。总体形状参数的置信区间为(2.020， 2.060)，回归参数的置信区间为(-11.278 -12.265)，总体尺度参数的置信区间为(266.2， 385.6)。

由此可见用此法来确定和及的置信区间的精确度还是相当高的，但无法确定安全寿命(位置参数)的置信区间。此法确定威布尔分布中形状参数的置信区间是有效的，且由此可检验样本是在某种置信度下是否符合威布尔分布。虽然可按照线性回归来给出回归直线的置信区间和预测区间，但只能是在对数坐标系中进行，效果显然没有在非对数坐标系中好，第5节就来解决在某个可靠度之下疲劳寿命的置信区间。

5 威布尔分布的置信区间:方法2

为解决第4节未解决的问题，需要引入秩分布。事实上，可设,,…,为相互独立且来自同一总体的随机变量，且有<<…<, 设为小于第个发生的频率值，那么容易得到第个随机变量的概率密度函数为

(39)

即可得

()～Be(,-+1)=

-1(1-)-/(,-+1)

(40)

式中：Be(,)为贝塔分布的概率密度函数

Be(,)=-1(1-)-1(,)

(40a)

其中：(,)=(+)(()())为贝塔函数，(·)为伽马函数。

为得到置信度为的置信区间，按文献[6] 分别设U,L为置信上限和下限：

(41)

由此的置信区间为

(42)

式中：≥50%。再由式(41)得

(43)

做变量替换=-+1=1-，注意到的定义式(39)及贝塔分布的定义式(40a)，即式(43)可变为

和式(41)的积分限做比较即得

L=1-U(-+1)

(44)

有了式(44)可节省一半计算量。在文献[11]中分别给出了=0.90和=0.95不同的之的表，可以想象在差不多30年前的条件下要计算这些数值是非常不容易的事情，最大问题还在于使用是很不方便的，这大概也是这种方法推广不易的原因之一。而现在计算机硬件、软件如此发达，计算和使用这些数值完全不需要查表，能够非常智能化地做到“按需供给”，非常方便人们使用，当然算法的基础还是高镇同法。

用例3的数据，用Python代码可得，在置信度=0.95、=20的条件下的置信上限:13.91，21.61，28.26，34.37，40.10，45.56，50.78， 55.80，60.64，65.31，69.80，74.13，78.29，82.27，86.04，89.59，92.86，95.78，98.19，99.74。在置信度=0.95、=20 的条件下的置信下限:0.26， 1.81，4.22，7.14，10.41，13.96，17.73，21.71，25.87， 30.20，34.69，39.36，44.20，49.22，54.44，59.90，65.63，71.74，78.39，86.09。按平均秩计算得到的参数：=2.040，=320.98，=276.60，=0.999 22， 按上限秩计算得到的参数：=2.797，=368.96，=158.80，=0.998 97，按下限秩计算得到的参数：=1.986，=343.26，= 333.06，=0.999 26，总体形状参数=2.040 的置信区间为[1.986， 2.797]，总体安全寿命参数=276.600的置信区间为[158.800， 333.060]，可靠度=0.999对应的安全疲劳寿命= 287.459 置信区间为[190.019， 343.658]。

在此得到的结果和文献[13]中的结果几乎是一致的，改进了他们的工作，将其智能化了，并且将疲劳寿命的置信曲线都画出来了，用起来非常方便，且不易搞错。只要将=0.95换为0.9马上可得如下结果：

在置信度=0.9、=20 的条件下置信上限:10.87，18.10，24.48，30.42，36.07，41.49，46.73，51.80，56.73，61.52，66.18，70.71，75.09，79.33，83.41，87.31，90.98，94.36，97.31，99.47。在置信度=0.9、=20的条件下置信下限:0.53，2.69，5.64，9.02，12.69，16.59，20.67，24.91，29.29，33.82，38.48，43.27，48.20，53.27，58.51，63.93，69.58，75.52，81.90，89.13。按平均秩计算得到参数：=2.040，=320.98，=276.60，=0.999 22，按上限秩计算得到参数：=2.513，=336.90，=204.20，=0.999 05，按下限秩计算得到参数：=1.946，=329.56，=327.74，=0.999 31，总体形状参数=2.040 的置信区间为[1.946， 2.513]，总体安全寿命参数=276.600的置信区间为[204.200， 327.740]，可靠度=0.999对应的安全疲劳寿命=287.459的置信区间为[225.777， 337.219]。

与=0.95的结果比较可发现置信度减少了，那么置信区间会“缩短”，看起来目标收窄了，但命中率(置信度)也小了，可谓“鱼与熊掌不可兼得”也，必须权衡利弊，这也是在一般情况下人们喜欢选取置信度为0.95的原因。图3和图4分别为置信度为0.95和0.9的威布尔分布置信限曲线。

图3 置信度为0.95的疲劳寿命置信限曲线Fig.3 Graph of confidence limit for fatigue life with 0.95 confidence

图4 置信度为0.9的疲劳寿命置信限曲线Fig.4 Graph of confidence limit for fatigue life with 0.9 confidence

在此有几个问题需要强调一下：

1) 前面所说的置信限是对于分布函数而言的，而对于可靠度=1-。因此对来讲的置信限正好与可靠度的置信限相反，即由的置信上限得到了的置信下限。

2) 对于安全寿命参数的置信区间也是与可靠度一致的，即需要“颠倒”。但形状参数的置信区间却因为与位置参数是负相关的，因此与可靠度相反，反而与的置信限是“一致”的。不难看到在同样置信水平的条件下由第4节中得到的关于的置信区间要比此节得到的长度要短，即要好一些。其原因大概是前者是直接计算得到的，而后者是间接得到的。

3) 另外一个问题要注意，这里没有给出尺度参数的置信区间，这是因为威布尔分布的3个参数的确定往往是有关联的。先是由相关系数极大化来确定出位置参数，然后再由最小二乘法确定出形状参数, 最后才间接求出尺度参数λ。因此得到的所谓其置信区间就没有什么意义了(至少用这个方法是得不到的)。从计算的结果也可看到这一点，由平均秩计算出来的=320.98，居然不在由秩的上下限计算出来的的区间[329.56,336.9]里。其实对于实际应用来说最重要的是由确定的可靠度来定出疲劳寿命的置信区间。

最后来回顾一下人们对威布尔分布的置信区间的认识是有必要的。由于3参数数学形式的复杂性，对于3个参数的点估计就存在一定困难，而对于参数的置信区间的估计就难上加难，因此从双参数的威布尔分布入手是不奇怪的。但其方法还是比较麻烦，使用起来并不方便，更加重要的是双参数忽略威布尔分布中的安全寿命这个参数，无论是理论还是实际应用都是欠缺的，当然不是没有人去讨论3参数的置信区间问题，应该说文献[6]的观点是正确的，只是使用起来不方便，这一节利用高镇同法将其计算方法加以改进，使用起来就没有问题。文献[18]的观点是正确的，但要回到“图解法”是不可取的。而文献[19]中给出的3参数置信区间所谓近似方法也是相当麻烦的，且不说在实际应用中好不好用，最大问题还在于给出的例子是无法“重复”的。至于文献[20]例子中的威布尔分布3参数若用高镇同法是100%和真值相同，而用该论文的方法还是存在误差，尽管误差不算大，其他例子也存在同样问题。其提出用自助法来优化置信区间的思想是可取的，但没有讲清楚如何得到得到威布尔3参数点估计的具体方法，而这恰恰是最基本的。

6 结束语

将大样本数据进行分组实在是某种“无奈之举”，其中一个目的在于检验数据是否服从正态分布，过程相当麻烦，而且一旦检验出不服从，就没有下文了。在疲劳统计学中研究的数据若不服从正态分布，那么在一般情况下往往是符合威布尔分布。此时可用高镇同法通过相关系数或决定系数的大小来判定样本数据服从威布尔分布是否更合适，且根本无需将数据“分组”。

当然不服从威布尔分布也可能是属于其他类型的分布，可根据第4节中给出的方法做一个关于形状参数的t检验，以确定在一定的置信度该数据是否属于威布尔分布。

由于威布尔分布的3个参数具有内在的某种复杂的非线性关系，因此很难同时给出3个参数的置信区间(这个问题将在另一篇论文中解决)。而只能提供可靠度的上下限置信曲线，实际上是提供了在一定可靠度下疲劳寿命的置信区间，而这个置信区间恰恰是人们在解决可靠性问题中最想知道的信息！这也是一个智能化解决方案，其基础仍然是高镇同法。

从更深层次的角度看，一组数据或者说一个样本，从本质上讲是该数据的总体在某个参照系(维度)上的投影。利用各种统计方法就是希望从这个投影中找到其总体的庐山真面目。如果总体比较简单，比如就是一个简单的高斯分布，投影又没有受到“扭曲”，那么就比较容易判别出其总体的高斯分布的2个主要参数。但如果不是高斯分布，或者即使是高斯分布投影受到扭曲，比如数据不够多，或者只是投影“片面”的数据，那么就很难得出关于其总体属于何种分布的结论。其实所谓高斯分布也好、威布尔分布也好或者其他分布也好，都是人类在经验中总结出来的分布，是人们用来描述世界的工具。在许多场合中是有效的，但极有可能在某些场合中是不那么有效甚至无效的，即不存在无条件是正确的东西。统计的任务是在不确定中寻找一定条件下的某种确定性，某种能够量化的东西，那就是“概率”。本文也是一样，无法提供区分高斯分布和威布尔分布的绝对标准，只能是提供与理想可靠度决定系数的量化标准，在给定的置信度和可靠度之下疲劳寿命的置信区间。

文献[1]和本文取得一些成果仅仅是疲劳统计学智能化的一个“开始”，还处于“初级阶段”。希望能起到抛砖引玉的作用，在不远的将来能看到取得更多的智能化成果。

致谢

感谢万伟浩先生对有关研究工作的全力支持。感谢鲍蕊教授无私的帮助和指导。