联合调频率拐点与FrFT的多分量LFM干扰抑制方法

戚连刚，韩颜泽，王亚妮，国强，Kaliuzhny MYKOLA

1. 哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001 2. 中国电子科技集团公司第十研究所 敏捷智能计算四川省重点实验室，成都 610036 3. 先进船舶通信与信息技术工业和信息化部重点实验室，哈尔滨 150001 4. 哈尔科夫国立无线电电子大学，哈尔科夫 61166

全球卫星导航系统(Global Navigation Satellite System, GNSS)补充了机载惯性导航系统，在全球范围内提供航路、终端和进近期间的引导服务，已成为现代飞机导航的主要技术之一。相对于陆地和海上运输而言，航空运输对于GNSS的性能要求最高，由于各种恶意和无意识干扰的存在，航空应用中GNSS的可靠性和安全性成为了重要的研究方向。在航空领域中，机载导航设备的天线数量受限且不能与其他机载无线接收机产生额外干扰，对于这一类定位精度和硬件资源受限的环境，单天线卫星导航接收机具有独特优势。

线性调频(Linear Frequency Modulation, LFM)干扰信号具有宽带非平稳特性，是一种通信、导航、雷达系统面临的典型干扰。单天线接收机不具备空间分辨能力，主要采用变换域分析手段抑制LFM干扰，其中较有效的变换方法有：短时傅里叶变换(Short-Time Fourier Transform, STFT)、小波变换(Wavelet Transform, WT)、Wigner-Ville分布(Wigner-Ville Distribution, WVD)、分数阶傅里叶变换(Fractional Fourier Transform, FrFT)等。这些方法利用干扰信号与导航信号在变换域的能量分布差异，通过滤波器或脉冲消隐等手段实现干扰抑制；为了进一步提高导航接收机的抗干扰能力，文献[9]根据线性调频斜率自适应的调节STFT窗长，并通过多组窗叠加的方式缓解了STFT时频分辨率不足的缺点；文献[12]采用时频图对调频率拐点位置进行估计，通过多个周期的短时R’enyi熵缓解了干扰频率估计结果受调频率拐点影响较大的问题。虽然这些方法提高了GNSS接收机对单分量LFM干扰的抑制能力，但当多个分量的干扰同时存在时，跟踪瞬时频率的方法受交叉项影响较大。FrFT减少了交叉项带来的影响，但是数字FrFT的非线性失真及干扰相位不连续引起的分数谱泄漏导致干扰抑制后残留干扰能量较大，文献[13]提出重叠加窗FrFT联合时域消隐的方法并用于直接序列扩频系统中减少了残余干扰，文献[14]通过FrFT域幅度一阶矩快速求取最优阶数并对单分量LFM干扰进行抑制。目前存在大量的FrFT最优阶数的快速搜索算法，如文献[15]提出的黄金分割与文献[16]提出的四阶原点矩等方法，这些方法提高了FrFT最优阶数的搜索速度。在多分量干扰抑制过程中，为了减少期望信号的信噪比损失，干扰需要按能量逐次去除。然而，在实际应用中干扰的周期信息与干噪比未知，分数阶傅里叶最优阶数快速搜索方法会受到调频率拐点影响，且基于整体均值统计的底部噪声能量估计方法的自适应性不足，难以应对不同干噪比情况。

为了进一步减少残余干扰对接收信号后续处理带来的影响，提高单天线导航接收机在不同干噪比下的适应性，本文针对典型FrFT类方法的不足，提出一种联合调频率拐点信息与FrFT的多分量LFM干扰抑制方法，通过优化多分量LFM干扰信号的分数阶傅里叶最优阶数搜索区间，减少残余干扰的影响。首先提出了一种基于时域差分与奇异值分解的调频率拐点估计方法，提取干扰信号的周期信息，并根据调频率拐点索引值对信号分块；其次，利用干扰中心区间的接收信号进行最优阶数估计与自适应门限估计，提升干扰抑制效果。仿真分析表明，该方法对于单个分量与多个分量LFM干扰均有改善，可以减少干扰抑制过程的信噪比损失，提升导航信号捕获效果。

1 问题模型

1.1 信号模型

单天线卫星导航接收机处理的数字信号可以表示为

(1)

式中：()表示第颗卫星的导航信号；()为LFM干扰信号；()为接收机热噪声。接收机处的第颗卫星的导航信号表示为

(2)

式中：表示接收机处第颗卫星导航信号的功率；(·)表示导航电文数据序列；(·)表示扩频码序列；表示含多普勒频移的中频载波频率；表示载波相位。

多分量LFM干扰可以表示为

(3)

式中：表示干扰分量序号；为分量个数；为第个干扰分量第个周期序号；为第个干扰分量的周期总数；为第个干扰分量第个周期长度，令=0；,()为第个干扰分量的单个周期内信号，其数学模型可以记为

,()=ei(2π+π+)0<≤

(4)

式中：为干扰振幅；为初始频率；为调频斜率。

1.2 分数阶傅里叶变换特性

分数阶傅里叶变换定义为

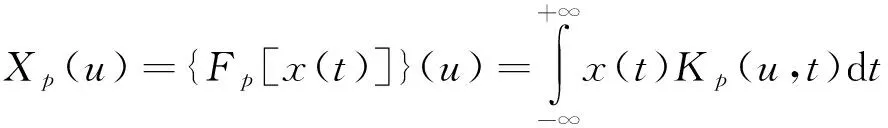
(5)

式中：{[()]}()表示对()做阶FrFT到域，=2π为FrFT的阶次，为旋转角度；[·]为FrFT算子；(,)为FrFT变换核。

对应旋转角度的FrFT为

(6)

式中：当=-cot、=csc时，()的分数阶傅里叶谱峰为

(7)

LFM干扰的主能量可以通过阶FrFT提取，而卫星导航信号为经过随机序列扩频后的信号，在任何一个FrFT域的分布类似于高斯白噪声分布，因此可以利用LFM干扰和卫星导航信号在FrFT的聚集特性差异实现干扰抑制。其中FrFT变换阶数可以通过峰值搜索来获取，峰值搜索算法需要记录不同阶数下的峰值并取其中的最大值。实际应用中，单次FrFT变换长度有限，需要对接收信号进行截断后分批处理，而信号截断区间对LFM干扰在FrFT域聚集情况有较大影响，当信号中存在多个LFM干扰分量时，通常需要按干扰能量逐次消除干扰，由式(7)可得，LFM干扰信号在最优旋转角度的分数谱最高峰值大小取决于信号能量与时域截断长度，当截断区间不同时，其一维搜索空间会发生变化，如图1所示。2分量LFM信号干扰参数与调频率拐点位置不同，假设分量1幅值为1 V，分量2幅值为0.5 V，2个虚线框分别表示不同位置的2个最优阶数搜索窗口，前者意味着处理窗口中的信号包含调频率拐点，后者表明窗口中不存在调频率拐点。可以发现当截断区间内包含调频拐点时，分数阶傅里叶阶数搜索方法难以区分不同分量的干扰强度，会对快速搜索算法和干扰抑制效果产生影响。

图1 不同区间的FrFT域最优阶数搜索情况Fig.1 Results of search of optimal order in FrFT domain in different intervals

1.3 LFM信号时域差分与奇异值分解特性

由欧拉公式可得，单个连续调频斜率对应的LFM干扰信号可以表述为

()=cos(2π+π)+

isin(2π+π)

(8)

将采样得到的含干扰的导航信号延时后，再与原信号相减可得：

()=()-()=

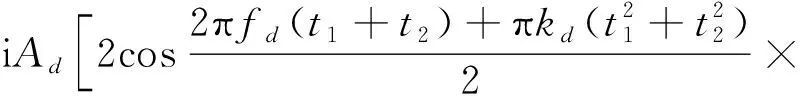
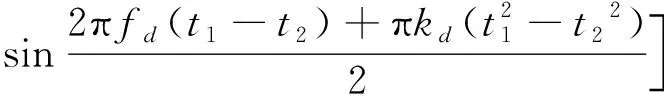
(9)

所得()乘自身共轭得：

()=

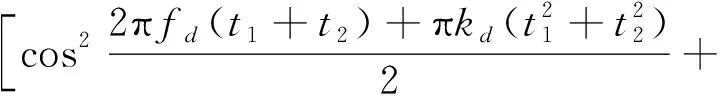
(10)

延时长度取一个采样间隔，即-=，为采样间隔，令=1,2,…，则时域差分幅值为

()=

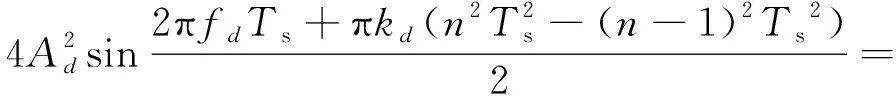
(11)

由于数字化采样得到的LFM信号满足=1>2(+)，为LFM干扰带宽，为采样频率。对于LFM干扰信号，有=(·)，为单个周期的总采样点数，代入式(11)可得：

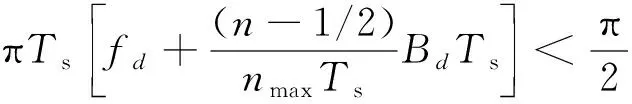
(12)

由式(12)可得时域差分幅值()在单个LFM干扰片段内满足三角函数特性且单调性递增。对于多分量LFM干扰，时域差分过程会产生交叉项，即

(13)

式中：·表示共轭。对于混有交叉项的()，构造×(-)阶Hankel矩阵，其中<-，为数据总长度，即

=

(14)

对矩阵进行奇异值分解，可表示为个秩为1的×(-)阶矩阵和

(15)

式中：为矩阵奇异值，且有≥≥…≥≥0；为的第个左奇异值向量；为的第个右奇异值向量。

Hankel矩阵SVD可以将信号不同频率分量映射进不同子空间中，能够实现不同频率分量的分离。当不同分量干扰能量与带宽不同时，经过时域差分处理后的各差分分量和交叉项的频率不同，因此，可以通过提取最大奇异值对应的分量减少交叉项带来的影响，可表示为

==[1,1,](-)×

(16)

式中：1,为的第元素；1,为的第元素。通过重构得到

=[,，…，1,(-),

1,(-)，…，1,(-)1,]

(17)

其局部峰值点为LFM干扰调频率拐点位置。

2 联合拐点信息与FrFT的LFM干扰抑制

考虑到传统基于FrFT的干扰抑制方法在处理周期LFM干扰时搜索过程受调频率拐点影响，去除残余干扰时门限受干噪比变化影响较大，本文提出了一种联合调频率拐点信息与FrFT的多分量LFM干扰抑制方法，处理流程如图2所示。对于检测存在LFM干扰的接收信号，首先，通过时域差分处理将周期LFM干扰转换为不同分量的周期信号叠加，通过等距降采样减少数据长度，利用奇异值分解获取不同分量对应的LFM干扰的调频斜率拐点位置；其次，根据拐点索引信息选取区域搜索FrFT最优阶数，在FrFT域消除干扰；最后，通过索引区间估计底部噪声能量大小，在时域消除残余干扰。

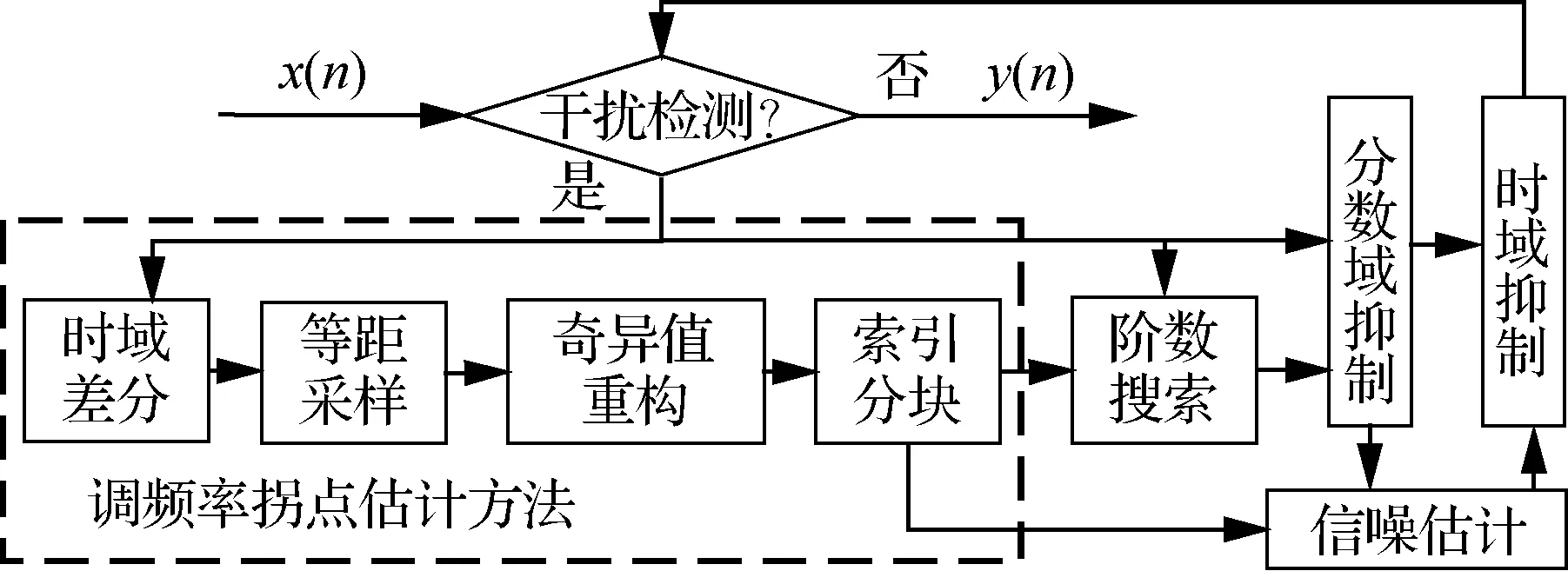
图2 所提方法流程框图Fig.2 Block diagram of proposed method

2.1 所提算法实施步骤

结合1.3节的分析，所提方法每处理一个分量的LFM干扰算法如下：

由式(9)～式(11)获取信号时域差分幅值：()=[()-(-1)]·[()-(-1)]。

对()等距采样，并根据式(14)构建Hankel矩阵，对矩阵进行SVD分解，保留最大奇异值进行矩阵重构，由式(17)获取重构信号。

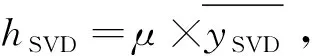
选取干扰中心区间进行最优阶数搜索，并在FrFT域进行干扰抑制，获取干扰抑制后的信号′()。

2.2 所提算法复杂度分析

对于长度为的接收信号，以算法实施过程中所需乘法次数衡量本文所提方法的复杂度。在FrFT前进行了调频率拐点估计，其中时域差分处理一次需要进行的乘法运算次，对差分结果进行奇异值分解，由于奇异值分解复杂度主要与所需奇异值个数和数据长度相关，当奇异值个数较少时，复杂度较低，由于LFM信号差分结果具有周期性且频率远低于采样频率，因此可对差分结果进行降采样，以减少运算复杂度。假设每批次等距采样获取的数据点长度为，分解获取的奇异值个数为，即×(-+1)阶Hankel矩阵。对矩阵进行奇异值分解，获取矩阵的奇异值需要(-+1)+3-3次乘法，获得左右奇异值向量并与最大奇异值重构为估计分量需要(-1)+2(-1)次乘法。获取调频率拐点索引需要一次均值统计，按索引对信号分块提取不需要乘法操作。对信号进行重叠加窗的FrFT，复杂度主要由FrFT操作次数决定，所提方法提取干扰中心位置对阶数进行估计，共需要(4+)(6log+3)+4，其中假设为FrFT窗长，为搜索最优阶数所用平均次数。对信号根据索引区间进行底部噪声能量估计需要每个拐点对应2次均值统计，采用门限置零的方法去除残余干扰不需要乘法次数。综上，所提方法每处理一个分量共需要(-+1)+5(-1)+(-1)+4+(4+)×(6log+3)+2次乘法运算，为调频率拐点个数。

3 仿真实验与结果分析

实验分析中，模拟接收机环境温度为290 K，采用全球定位系统L1频段的C/A码信号，输入功率为-130 dBm，输入带宽为2.046 MHz，下变频后信号中心频率为2.048 MHz，采样频率为10.24 MHz，输入端信噪比为-20 dB。由于本文所提抗干扰方法主要应用在解扩前，不涉及多个卫星信号处理过程，故只考虑一个卫星导航信号的情况。

LFM干扰参数如表1所示，其中多分量LFM干扰分为干扰分量1与分量2能量相差5 dB 的场景1与能量相同的场景2这2种情况，仿真曲线中多分量的干噪比为能量最大分量对应的干噪比。

表1 干扰信号参数Table 1 Interfering signal parameters

3.1 时域差分与奇异值分解的处理结果

对于LFM干扰，图3和图4展示了单分量与多分量场景下的调频率拐点估计效果，其中单分量场景干噪比为10 dB，多分量干噪比为15 dB的场景1，奇异值个数=20，等距采样间隔设置为5个采样点。图3(a)和图4(a)为应用文献[9]所提出的改进STFT方法生成的信号时频图，由于导航信号与噪声能量相对较小，因此时频图中主要包含干扰信息。

图3(b)为含干扰信号的时域差分结果，当干扰能量较弱时，单分量LFM干扰调频率拐点区间估计效果主要受噪声影响，部分非拐点位置的时域差分幅值高于拐点处幅值，图3(c)为奇异值重构结果，可以发现奇异值分解能有效缓解由噪声引起的不具备周期特性的异常点对估计结果的影响。图4(b)为多分量LFM干扰场景下信号时域差分结果，当干扰为多个能量相近的分量时，拐点估计效果同时受交叉项与噪声影响，图4(c)为多分量场景下的奇异值重构结果，奇异值分解可以提取多分量场景下的调频率拐点信息。去除干扰分量1后，在对分量2进行估计时受残余干扰影响较大，可通过奇异值分解获取干扰周期信息，直到检测不出LFM干扰分量。对于单分量LFM干扰，奇异值分解可以有效提升估计方法的抗噪性能，对于多分量LFM干扰，奇异值分解可以提取不同分量的调频率拐点位置信息。

图3 单分量LFM干扰调频率拐点估计Fig.3 Estimation of chirp rate turning point of single component LFM interference

图4 多分量LFM干扰调频率拐点估计Fig.4 Estimation of chirp rate turning point of multi-component LFM interference

图5给出几种场景下，不同干噪比对应各分量拐点索引区间的获取准确度，这里定义正确率为调频率拐点位于拐点索引区间的数量与调频率拐点总数量的比值。对于周期性的奇异值分解结果进行峰值检测，可以通过统计序列均值结合门限权值估计调频率拐点所对应的局部峰值区域。如果门限权值较大，会造成某些调频率拐点漏检，而门限权值过小则会导致调频率拐点估计范围过大，以及将某些噪声引起的峰值估计成调频率拐点。为适应不同干噪比干扰，选取门限权值=12。

图5 调频率拐点区间估计正确率Fig.5 Accuracy of chirp rate turning point estimation

如图5所示，由于导航信号与噪声的差分结果不含周期性与单调性，只有当干扰与噪声能量相近时，单分量场景拐点的调频率拐点估计结果受影响较大。对于多分量干扰，由于存在交叉项的影响，估计效果受干扰能量影响。其中场景1由于2个分量能量不同，对能量较高的分量1的估计效果优于场景2，但分量1的干扰残余对分量2的估计容易产生较大影响。而对于场景2，由于2个分量能量相同，可根据带宽与起始频率差异区分不同分量，同时对于分量2的估计受分量1残余影响较小。对于不同分量干扰能量相差较大的场景，能量较低的分量受能量较高的分量残余影响较大，但此类场景不需要对干扰能量进行区分。对于干扰能量相同且起始频率与带宽均相近的LFM干扰，所提方法难以区分干扰分量，会将不同分量的调频率拐点归为同一个分量，但依然适用于后续处理。

3.2 基于调频率拐点的时域去脉冲效果

目前FrFT多采用重叠加窗的干扰抑制方法，在加窗减少频谱泄露的基础上，通过重叠处理技术减少窗函数引起的输入信号畸变。由于LFM干扰存在调频率拐点处相位不连续的现象，会造成干扰信号在分数阶傅里叶域扩展，去除干扰所在的主瓣能量后，残留的能量在逆变换回时域后会在调频率拐点处表现为脉冲形式，LFM干扰干噪比越高，残余干扰带来的信噪比损失越明显。

对于多分量LFM干扰，需要对其各自对应的阶次进行干扰抑制，抑制干扰的残留能量会对后续干扰信息的估计与抑制带来影响。对于残余的脉冲干扰，传统方法有基于均值统计与基于连续均值去除的自适应门限方法，其中基于均值统计的方法通过一次或两次均值统计，获取全局门限用于时域置零，这种方法实现简单直接，适用于对复杂度要求较高的干扰抑制流程。但当干扰周期长度和干噪比变化时，难以在不同情况下均达到较优的效果。基于连续均值去除的方法，是一类自适应迭代的脉冲干扰抑制方法，由于没有背景噪声功率的先验信息，因此通过块内迭代估计底部噪声功率，这种方法对迭代过程的要求较高，计算复杂度高。

由于残余脉冲干扰来自LFM干扰周期间相位跳变，残余脉冲的位置与调频率拐点一一对应。传统基于均值统计的方法由于缺乏残余干扰位置的先验信息，通常需要对整体信号进行均值统计以获取门限，这一类方法对干噪比不同的场景自适应性较差。所提方法通过调频率拐点区间索引值作为先验信息估计底部噪声功率，可以在不使用迭代估计的情况下保证后续的同步稳定性。

图6给出了干噪比为10～40 dB下，本文所提方法与传统基于均值统计方法的局部效果图。对于残余脉冲干扰，文献[13]提出通过脉冲消隐的方式进行抑制，并提出幅度的均值乘以系数的门限计算方法，给出了门限权值范围∈(2,3)。

图6 残余干扰抑制效果Fig.6 Residual interference suppression effect

如果权值过大会造成干扰残余较多，而权值过小则会导致期望信号损失太多，结合实验测试结果，选取门限值为=25。从图6中的残余干扰幅值可以看出，不同干噪比下传统方法计算获取的门限受残余干扰能量影响较大，所提方法通过调频拐点区间获取干扰抑制门限，可以通过干扰时域信息提高不同干噪比场景下的残余干扰消除效果。

表2分析了2种去残余方法处理后的均方误差，由不同干噪比下的均方误差可得本文所提方法能在误差相近的情况下改善干扰抑制效果，做到更精确地去除残余干扰。

表2 归一化均方误差Table 2 Normalized mean square error

3.3 输出信干噪比与捕获效果

干扰抑制后，输出信号与噪声及残余干扰能量之比直接决定后续的性能，尤其对于单天线导航信号接收机，由于其低空间成本和硬件成本，往往采用级联技术抑制多个干扰，低信干噪比损失更有利于后续的信号处理。对于传统FrFT方法与本文所提方法，采用文献[15]的阶数搜索算法与文献[13]的FrFT域处理流程，FrFT窗长为512个采样点，通过100次蒙特卡洛实验，对干扰抑制处理后的输出信干噪比(Signal to Interference-plus-noise Ratio, SINR)与捕获因子(Acquisition Factor, AF)进行分析，其中捕获因子为GNSS信号捕获后的最大相关峰值和第二相关峰值之比，相干积分时间为9 ms。

图7给出了不同场景下，输出信干噪比随输入干噪比变化的曲线，随着干噪比增大，输出信干噪比明显减小，这是由于干扰能量越大，FrFT域能量扩散对期望信号的影响越大，其中多分量由于需要逐次干扰消除流程，信干噪比损失积累，抗干扰效果更差。由所提方法可以通过拐点估计对FrFT最优阶数搜索提供先验信息，对于多分量场景，能够保证优先处理能量较强带宽较大的干扰，减少对后续分量干扰抑制的影响，同时，根据干扰中心位置估计噪声能量用于获取时域抑制门限，可以有效增加干扰抑制方法对不同干噪比的适应性。如图7所示，随着干噪比增大，所提方法可以获得更高的输出信干噪比，而传统方法的效果恶化更为严重。

图7 不同场景下输出信干噪比Fig.7 Output signal to interference and noise ratio in different scenarios

由于干扰信号的残余和有用信号的丢失共同影响导航信号的捕获结果，因此可以通过捕获因子综合反映干扰抑制方法的性能。图8给出了不同干噪比对应的捕获因子，随着干扰能量增强，残余干扰导致捕获效果变差。

如图8所示，对于单分量LFM干扰，由于FrFT最优阶数搜索不需要区分干扰分量，因此本文所提方法只在时域去残余干扰阶段通过减少信噪比损失提升捕获效果。对于多分量场景，本文所提方法在场景1中提升效果更明显，这是因为2个分量的干扰能量不同时，干扰抑制的顺序更为重要。由于所提调频率拐点估计方法在低干噪比场景下效果受噪声影响较大，因此当干噪比较低时所提方法难以有较大提升。当干噪比小于20 dB时，干扰能量较弱，不同干扰抑制方法获得的干扰抑制效果相近，但随着干噪比的增大，在传统方法中由调频率拐点所引起的残余干扰能量越大，导航信号信噪比损失严重，所提方法能够有效消除调频拐点引起的残余干扰，干扰抑制性能改善明显。

图8 不同场景下干扰捕获效果Fig.8 Acquisition factor in different scenarios

4 结 论

1) 理论分析及仿真结果表明，联合调频率拐点与FrFT的多分量LFM干扰抑制方法可以更优地选择干扰抑制顺序与底部信噪能量估计区间，减少单分量与多分量LFM干扰抑制过程中的信噪比损失，有利于单天线导航信号接收机级联其他抗干扰技术。

2) 实验结果证明了基于时域差分与奇异值分解的LFM干扰调频率拐点估计方法的可用性，该方法可以在干噪比大于10 dB时对多分量LFM场景调频率拐点信息进行估计，为后续干扰抑制流程提供先验信息。