基于损失函数的缩比模型冲击响应预报结果修正方法

王悦鑫，何欢,*，吴添，惠旭龙

1. 南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016 2. 南京航空航天大学 振动工程研究所，南京 210016 3. 上海宇航系统工程研究所，上海 210019 4. 中国飞机强度研究所 结构冲击动力学航空科技重点实验室，西安 710065

冲击碰撞广泛存在于航空航天领域，研究冲击载荷作用下结构的动响应及破坏特征，对飞行器的适坠性研究及结构的设计优化起着重要的作用。

早期的学者从理论上对梁板结构的动响应进行了研究，试图通过量纲分析建立结构响应与冲击载荷的关系。Johnson于1972年提出了损伤数，用来描述在冲击载荷作用下梁和板的动响应。Zhao在损伤数的基础上考虑了几何因素的影响，提出了响应数。然而，冲击过程是一个高度非线性的问题，结构的动态响应不仅与结构的几何尺寸和约束条件相关，还与材料的弹塑性性质及应变率效应等因素有关。Li和Jones考虑材料的应变硬化、应变率、温度等效应进一步拓展了无量纲数。Hu和Shi等将无量纲数应用于各种板和壳的动态分析，充分展示了无量纲数在描述结构动态响应方面的重要性。

对于飞机等大型结构，难以从理论上进行动响应分析，进行冲击试验是最直接的方法。然而全尺寸试验成本高、周期长、且易受试验条件和环境的限制，适当地进行缩比模型试验则可以大大减小研究成本，缩短研究周期。

在量纲分析的基础上，应用相似理论建立缩比模型与原型的相似关系是缩比模型设计中最常用的方法。当考虑材料的应变率效应时，传统的相似关系便得不到精确满足。在畸变因素存在的条件下，如何保证缩比模型对原型冲击响应结果的预报精度引起了相关学者的关注，并发展了不同的修正方法。其中最具有代表性的是基于VSG量纲体系提出的一系列修正方法，Oshiro和Alves以VSG(冲击速度、应力、冲击质量)代替传统的MLT(冲击质量、时间、几何尺寸)作为一组新的无量纲数，针对应变率效应提出了修正冲击速度的VSG间接相似法。该方法尽管可以明显减小缩比模型的预报误差，但是需要提前获取原型和缩比模型的响应信息，是一种间接相似方法，应用较不便。为了克服VSG间接相似法的缺点，Oshiro和Alves基于幂指数形式的Norton-Hoff本构方程，提出了VSG相似法。该方法虽然不再需要预先获取原型和缩比模型的响应信息，但是仅适用于幂指数形式的本构模型，不具有普适性。

在实际工程中，可能会出现缩比模型与原型材料不同的情况，针对这种材料畸变问题，Oshiro和Alves提出了VSG材料畸变相似法，旨在利用应变率不敏感缩比模型预报应变率敏感原型的响应。该方法的提出意味着即使原型和缩比模型材料不同，也可以通过修正冲击速度减小缩比模型的预报误差。VSG材料畸变相似法由于是基于VSG间接相似法提出的，因此具有一定的局限性。Mazzariol等针对应变率效应以及材料畸变问题，通过在VSG体系中增加质量的无量纲数，提出了VSG-D相似方法。针对应变率效应，VSG-D方法比VSG相似法适用于更多形式的本构方程。针对材料畸变问题，VSG-D方法比材料畸变相似法更具有普适性。但是文中将结构的应变率设定为1 s，并未考虑冲击过程中材料应变率的动态变化。张振华等将VSG间接相似法应用于固支加筋方板在均布冲击载荷作用下的相似问题，通过数值模拟验证了该方法的有效性。徐坤等分析了应变率效应对冲击载荷下结构响应相似律的影响，并通过Taylor碰撞试验验证了VSG间接相似法修正效果。姜正荣等考虑应变率效应对单层网壳的冲击相似问题进行了研究，通过仿真验证了VSG法的有效性。包杰等以VSG作为基本物理量，针对应变率效应提出了一种改变缩比模型冲击质的修正方法，并将该修正方法应用于船舶-自升式海洋平台的碰撞分析中。胡晨晞以LST(几何尺寸、应力、时间)为基本物理量，结合间接相似法针对杆件提出了改变质量的修正方法，用来补偿应变率效应的影响。秦健和张振华考虑材料畸变和应变率效应的影响，研究了加筋板结构在水下爆炸冲击波作用下的相似问题，利用数值模拟验证了VSG材料畸变相似法的修正效果。苏子星和何继业考虑了应变率效应和材料畸变，对方板原型和2种不同材料的缩比模型进行了数值模拟，验证了VSG-D法的有效性。Sadeghi等利用一组连续介质力学的输运方程，提出了有限相似法，指出修正因子可以通过对数值方程加以条件约束来获得。在有限相似方法的基础上，Sadeghi等通过引入Johnson-Cook本构方程，考虑了材料屈服、应变硬化、应变率效应、热软化和材料失效对缩比模型预报的影响。王帅等利用DLV(密度、几何尺寸、冲击速度)代替VSG体系，通过建立应变率区间上缩比模型与原型的动态相似关系，利用直接相似的方法获得了修正速度或修正密度的比例因子，并研究了材料应变率敏感性特征参数、参考应变率、屈服应力、密度在动态相似关系中的作用。

在众多影响因素中，应变率效应是造成相似关系失衡的主要原因。然而，目前使用最广泛的VSG-D相似方法也未考虑材料应变率动态变化，因此缩比模型冲击响应预报结果修正方法仍有改进空间。本文针对缩比模型预报原型冲击响应出现偏差的问题提出了考虑应变率动态变化的损失函数法，在已知原型和缩比模型的几何尺寸及材料的情况下，利用损失函数法能够更好地补偿应变率效应造成的误差，进而准确预报原型的冲击响应。

1 缩比模型冲击响应预报结果修正方法

1.1 应变率效应对相似关系的影响

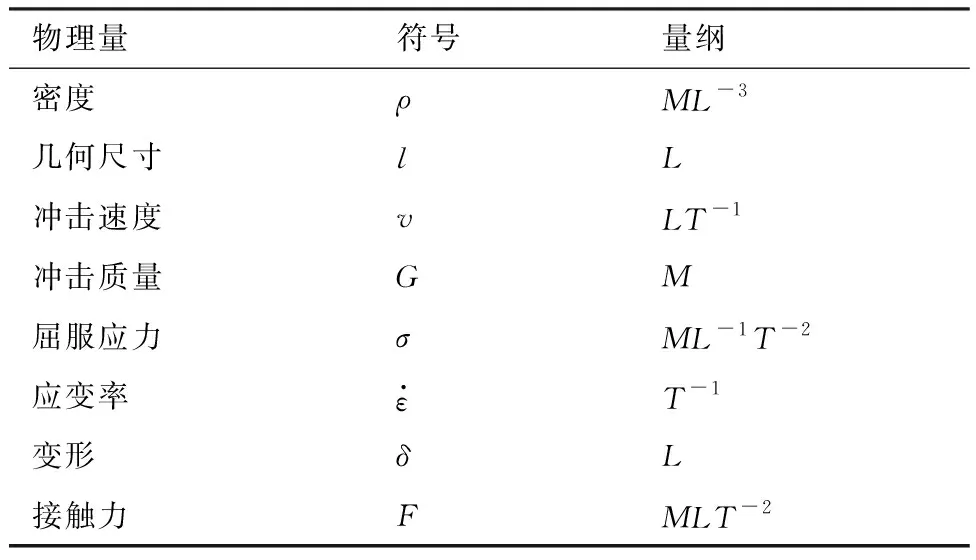
表1 各物理量的量纲Table 1 Dimensions for relevant variables

定义几何相似因子为

(1)

式中:下标m表示缩比模型，p表示原型。在传统的MLT体系中，常常利用单一的几何相似因子来联系缩比模型与原型，其他物理量的相似因子可以通过量纲分析给出，如表2所示。

通过表2可以得到缩比模型与原型的流动屈服应力关系：

(2)

式中：为流动屈服应力。

应变率关系：

(3)

假设材料的本构方程为

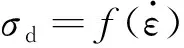
(4)

将式(3)代入式(4)有

(5)

表2 MLT体系中各物理量的相似因子

显然，式(5)与式(2)矛盾。说明当应变率满足相似关系时，缩比模型与原型的流动屈服应力之比不再等于1，而是随着几何相似因子和应变率的变化而改变，如图1所示。

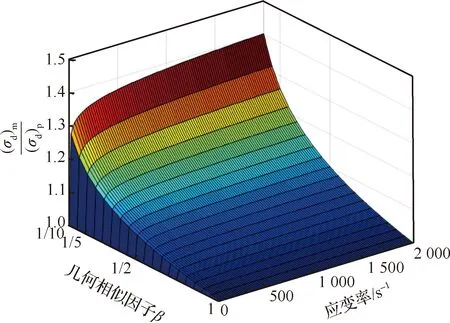
图1 缩比模型与原型的流动屈服应力之比随应变率及相似因子的变化Fig.1 Variation of ratio of flow yield stress of the scaled model and to that of the prototype with strain rate and scaling factor

1.2 考虑应变率效应后的相似关系

为了解决这个问题，现选取密度、几何尺寸、冲击速度作为基本物理量，由π定理，可求得

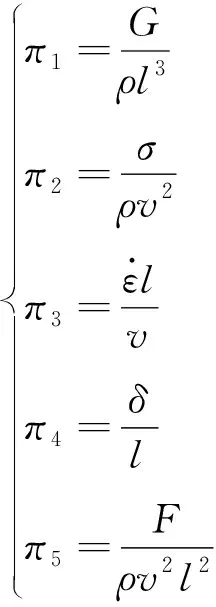
(6)

缩比模型由原型按照几何相似因子进行缩放，与式(1)同理，定义

(7)

将式(7)代入式(6)得到DLV体系中各物理量的相似因子如表3所示。

从表3可以得到缩比模型与原型的流动屈服应力关系:

表3 DLV体系中各物理量相似因子

(8)

应变率关系:

(9)

将式(9)和式(4)代入式(8)中，得到通过缩比模型预报的原型流动屈服应力为

(10)

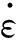
当原型和缩比模型的几何尺寸及材料确定，即和为常数时，不同应变率下流动屈服应力预报值与原型实际值的误差可以表示为关于的函数，即

(11)

现取()作为权函数，对式(11)在整个应变率区间内加权积分，可以得到整个应变率区间内流动屈服应力预报值与原型实际值的整体误差随变化的损失函数，即

(12)

(0)=min()

(13)

1.3 缩比模型冲击响应预报结果修正步骤

当几何相似因子和材料密度相似因子已知时，通过式(13)可以求得满足最小整体误差条件的速度相似因子，修正过程如下：

1) 确定相似因子和。

2) 通过仿真确定原型关键位置的应变率变化区间[,]。

3) 运用式(11)～式(13)计算得到速度相似因子。

4) 利用速度相似因子修正缩比模型的冲击速度，同时更新表3中变形和接触力等物理量的相似因子。

5) 进行缩比模型试验，得到缩比模型的变形和接触力等数据，利用表3中的相似因子计算原型冲击响应。

2 不同本构方程下的损失函数

2.1 Norton-Hoff本构方程

Norton-Hoff本构方程为

(14)

(15)

当原型和缩比模型的几何尺寸及材料确定，即，，，为常数时，利用式(13)可以得到满足最小整体误差条件的。

2.2 Johnson-Cook本构方程

忽略塑性硬化和温度的影响，考虑简化后的Johnson-Cook本构方程为

(16)

(17)

当原型和缩比模型的几何尺寸及材料确定，即、、、为常数时，存在使流动屈服应力预报值与实际值的整体误差最小。

2.3 Cowper-Symonds本构方程

Cowper-Symonds本构方程为

(18)

式中：为与材料应变率相关的参数，代入式(12)可得损失函数

()=

(19)

当原型和缩比模型的几何尺寸及材料确定，即、、、、为常数时，存在使缩比模型预报的流动屈服应力与原型实际值随应变率的变化趋于一致。

3 常用本构方程下不同方法精确度对比

假定几何相似因子=1/10，缩比模型和原型材料相同，材料实际应变率区间为[0 s, 2 000 s]。 现选用3种常用的本构方程，对比不同方法修正后缩比模型对原型流动屈服应力的预报精度。

3.1 Norton-Hoff本构方程

图2 Norton-Hoff的相对流动屈服应力-应变率曲线Fig.2 Relative flow yield stress-strain rate curves predicted by Norton-Hoff

3.2 Johnson-Cook本构方程

由于VSG方法仅适用于幂指数形式的Norton-Hoff本构方程，这里仅对比VSG-D方法和损失函数法的精确度。参考1006钢的材料参数，取=0.022。利用VSG-D方法解出= 1.027；利用损失函数法，代入式(13)可以求得=1.022。不同方法修正后缩比模型预报的相对流动屈服应力对原型的逼近效果如图3所示。显然当采用Johnson-Cook本构模型，且缩比模型和原型材料均为1006钢时，与VSG-D方法相比，损失函数法修正后的缩比模型更能准确地预报出原型相对流动屈服应力随应变率的变化。

图3 Johnson-Cook的相对流动屈服应力-应变率曲线Fig.3 Relative flow yield stress-strain rate curves predicted by Johnson-Cook

3.3 Cowper-Symonds本构方程

由于VSG方法的局限性，同样只给出VSG-D方法和损失函数法精确度的对比。参考Q235钢的材料参数，取=40 s，=5，代入VSG-D方法解得=1.067；利用损失函数法，代入式(13)可以求得=1.194。不同方法修正后缩比模型对原型相对流动屈服应力的预报效果对比如图4所示。不难看出，当采用Cowper-Symonds本构模型，且缩比模型和原型材料均为Q235钢时，本文方法得到的缩比模型相对流动屈服应力随应变率的变化与原型相符。当应变率为100 s时，本文方法预报误差最大为5.1%，此时VSG-D相似方法的预报误差为16.9%。随着应变率的增加，VSG-D相似方法预报精度持续下降。当应变率为2 000 s时，VSG-D方法流动屈服应力的预报误差达到23.5%，本文方法的预报误差仅为3.8%。由此可见，利用损失函数法可以非常准确地预报出原型的相对流动屈服应力。

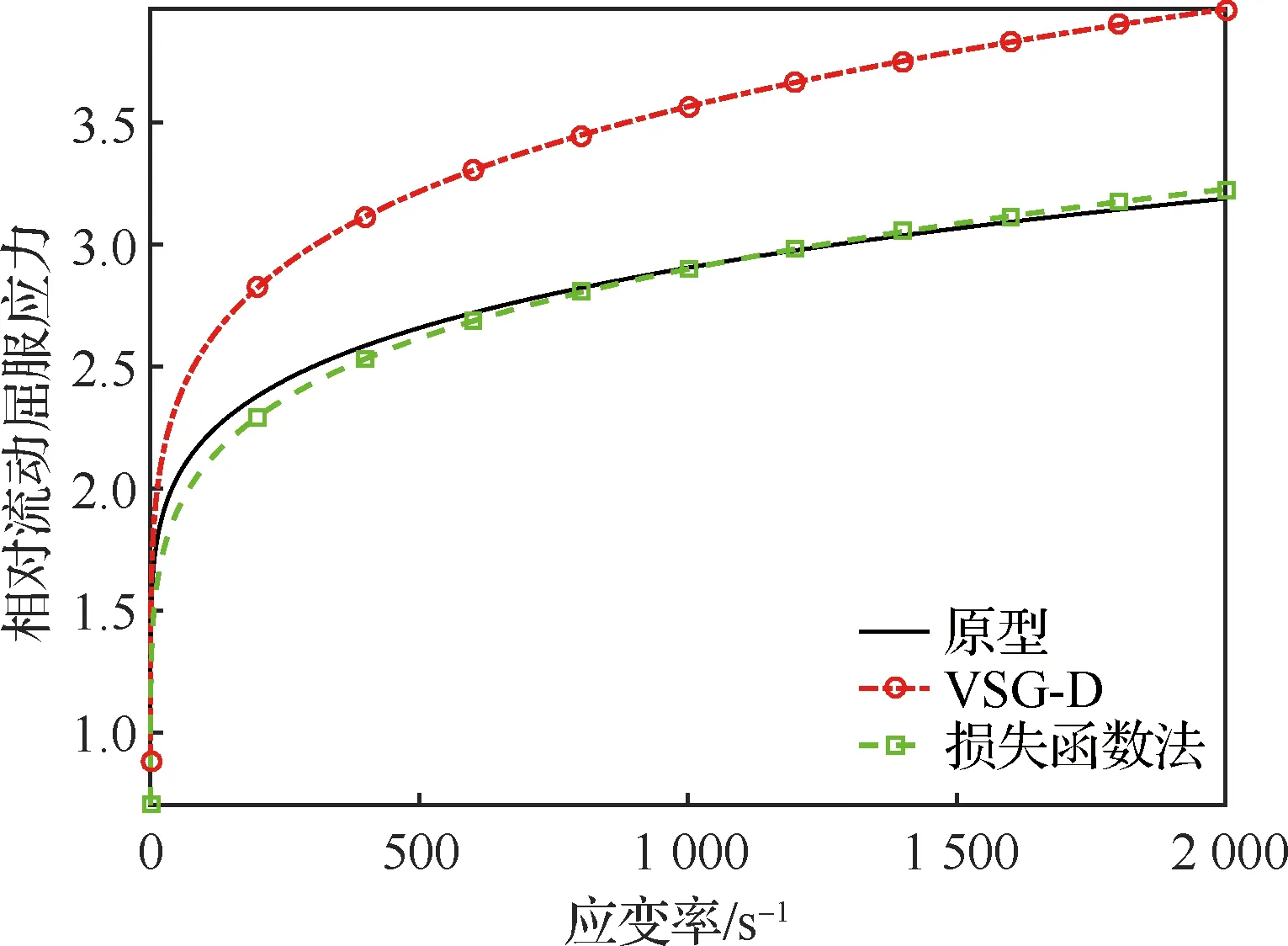
图4 Couper-Symonds的相对流动屈服应力-应变率曲线Fig.4 Relative flow yield stress-strain rate curves predicted by Couper-Symonds

4 数值模拟及试验验证

为进一步验证损失函数法对应变率效应畸变问题的修正效果，对受横向冲击的工字梁进行数值模拟及试验，并比较不同方法修正后缩比模型对原型响应的预报误差。

4.1 数值模拟算例

考虑图5所示工字梁，梁原型长=175 mm，高=20 mm，翼缘宽度=40 mm，腹板厚度=4 mm。工字梁受横向冲击，其中落锤质量为16 kg， 初始冲击速度为4 m/s，如图6所示。

图5 工字梁模型Fig.5 I-beam model

图6 工字梁受横向冲击示意图Fig.6 I-beam under transverse impact load

利用Ls-Dyna进行数值计算，落锤选用刚体材料MAT20进行模拟。缩比模型和原型均选用典型的应变率敏感材料Q235，材料模型选用MAT24。其中，MAT24材料以Cowper-Symonds 本构方程来考虑应变率效应，主要参数如表4所示。

表4 材料参数Table 4 Material parameters

计算得到原型和缩比模型的冲击动态响应时历曲线，不同方法修正后缩比模型对原型变形及接触力的预报结果如图7、图8所示。从图7(a)和图8(a)可以看出，缩比模型预报的变形较小，接触力较大，且峰值点时刻相对提前，与原型的冲击响应之间存在明显的差异。图7(b)和图8(b)是VSG-D方法修正的预报结果，可以看出VSG-D法在一定程度上减小了缩比模型的变形和接触力与原型之间的差异，对应变率效应具有一定的补偿作用。从图7(c)和图8(c)可以看到，当利用损失函数法进行修正时，缩比模型预报的变形和接触力时历曲线与原型基本吻合，相比于VSG-D法表现更好的修正效果。

图7 原型和缩比模型的变形时历曲线， 冲击速度v=4 m/sFig.7 Deformation-time curves of prototype and scale model， v=4 m/s

图8 原型和缩比模型的接触力时历曲线， 冲击速度v=4 m/sFig.8 Collision force-time curves of prototype and scale model， v=4 m/s

表5给出了不同方法修正后变形和接触力的峰值大小，图9给出了不同方法修正后的预报误差。结合表5和图9可以看出，当相似比为1/10时，修正前缩比模型预报的变形和接触力峰值误差分别为6.1%和6.28%，利用VSG-D法修正后分别降为3.19%和3.36%，而利用损失函数法修正后，修正效果更显著，误差分别降到1.21%和1.49%，说明损失函数法表现出更好的修正效果。

表5 不同方法修正后误差分析Table 5 Analysis of errors modified by different methods

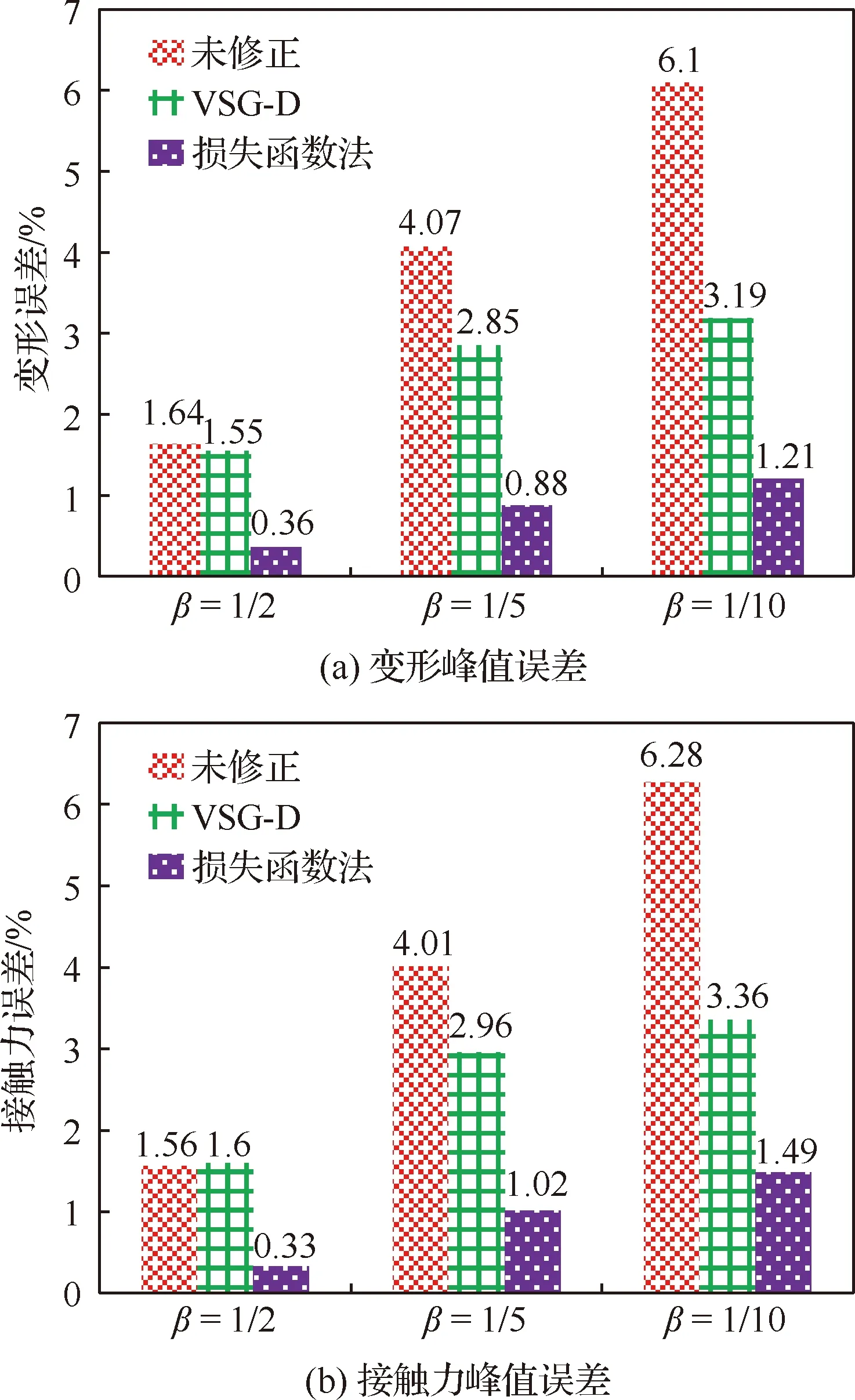
图9 不同方法修正后误差对比Fig.9 Comparison of error modified by different methods

现考虑不同冲击速度对预报精度的影响，设定落锤初始冲击速度为20 m/s，对图5所示的工字梁进行数值模拟。计算得到原型和缩比模型的冲击动态响应时历曲线，损失函数法修正前后缩比模型对原型变形及接触力的预报结果如图10、图11所示。

图10 原型和缩比模型的变形时历曲线， 冲击速度v=4 m/sFig.10 Deformation-time curves of prototype and scale model，v=4 m/s

图11 原型和缩比模型的接触力时历曲线, 冲击速度v=4 m/sFig.11 Collision force-time of prototype and scale model， v=4 m/s

通过对比损失函数法修正前后的变形和接触力时历曲线可以看出，对于受高速冲击的结构，利用损失函数法同样可以提高缩比模型的预测精度，减小预报误差。

4.2 试验验证

为验证损失函数法的准确性和仿真结果的可靠性，设定落锤初始冲击速度为4 m/s，对工字梁原型和相似比为1/2的缩比模型开展了冲击试验，得到了冲击变形特征与接触力时历曲线。其中，试验和数值仿真的变形结果对比如图12所示。

图12 试验与仿真的变形结果Fig.12 Deformation results of test and simulation

图13给出了原型和缩比模型的试验结果，可以看出未修正的缩比模型接触力时历曲线与原型之间存在明显的差异，峰值点时刻也相对提前。利用损失函数法修正后，缩比模型与原型的时历曲线吻合度明显提高，峰值点时刻以及接触力峰值也基本一致。

图13 原型和缩比模型的接触力试验结果， 冲击速度v=4 m/sFig.13 Collision force-test results of prototype and scale model, v=4 m/s

表6给出了数值模拟与试验的接触力峰值误差。从表中可以看出，试验与仿真的误差都未超过3%，可以认为仿真结果是有效的。结合试验和数值模拟的结果来看，利用损失函数法可以有效地减小缩比模型的预报误差，能够较准确地预报原型的冲击动态响应。

表6 接触力峰值对比Table 6 Comparison of peak collision forces

5 结 论

1) 本文针对应变率效应的提出的损失函数法不受本构方程形式的限制，同时考虑了材料应变率的动态变化。需要指出的是，本文在推导损失函数法的过程中并未涉及到损伤破坏的相关参数。若材料在冲击过程中产生损伤失效，本文提出的冲击响应结果修正方法仅限于对材料的弹性和塑性变形阶段给出高精度的响应预测结果，而不能用于产生破坏损伤之后的响应预测。

2) 对受横向冲击的工字梁开展了数值模拟和冲击试验，结果表明，相比于VSG-D方法，利用损失函数法可以非常准确地预报原型的变形和接触力等响应数据。

3) 考虑到实际工程中一般选择与原型相同的材料设计缩比模型，因此本文仅讨论了同种材料构造的缩比模型冲击响应预报结果的修正，对采用不同材料构造的缩比模型冲击响应预报结果的修正还需进一步研究。