基于平行线坐标变换的检测前跟踪算法

薄钧天，王国宏，于洪波，彭志刚

1.海军航空大学 信息融合研究所，烟台 26400 2.海军航空大学 青岛校区，青岛 266041

随着高科技军事技术的深入研究，通过使用隐身材料，设计特殊飞行器外形等技术已成为降低空中目标雷达散射截面积(Radar-Cross-Section，RCS)的主要方法，对现有雷达探测体系产生严重挑战。例如美国B-2轰炸机的RCS值低于0.4 m，世界第一型隐身战斗机F-117A的前向RCS值只有0.001 m。目前更有报道，更加先进的离子隐身技术和量子隐身技术正在研制。可以预见，未来隐身战斗机将在战争中发挥出及其重要的作用。

隐身技术的成熟使得此类飞行器相对雷达成为微弱目标，目前，针对微弱目标的探测多采用相参积累或非相参积累的方式，利用目标运动的时间连续性和帧间关联性，通过积累提高目标在较长时间内的整体回波能量后再进行峰值检测。检测前跟踪(Track-Before-Detect，TBD)方法是检测微弱目标较为有效的方式，通过先存储雷达量测信息，达到一定帧数后进行集中处理。目前主要有基于粒子滤波的PF-TBD技术，基于速度滤波的VF-TBD技术和基于Hough变换的HT-TBD技术等。这些方法各有优势，均能够对目标进行有效的检测。但是，基于粒子滤波的PF-TBD技术需要提升粒子数目以保证检测效果，实际应用中存在一定的限制；基于速度滤波的VH-TBD技术需要对目标速度进行准确的测量，实践中要求较高；基于霍夫变换(Hough Transform，HT)的HT-TBD技术在对参数单元进行网格化处理后，积累结果会出现峰值簇拥现象，不仅造成了积累损失，还需要后续更多的时间进行航迹修正，影响算法的检测概率和计算量。

本文提出一种基于平行线坐标变换检测前跟踪(Parallel-line-coordinate Transformation based Track-Before-Detect，PT-TBD)方法，通过在笛卡尔坐标系内设置平行轴线进行同坐标系的点到线转换，分割二维平面进行积累，提取峰值后进行航迹回溯得到最终的结果。由于Hough变换属于极坐标转换，而平行线坐标变换为线性变换，因此PT算法本身比HT算法有更低的运算量。仿真结果显示，PT-TBD算法产生的积累损失更小，具备更高的检测概率；与HT-TBD算法相比，PT-TBD算法提高了运行效率，在未来具备一定的应用和研究前景。

1 目标模型

检测前跟踪技术考虑的是在较短时间内，将目标航迹视作直线运动，通过对目标回波进行非相参积累进行检测。因此本文所设模型，均为短时间内沿直线的目标航迹。

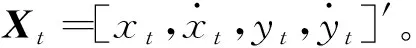
+1=,+1+

(1)

式中：=[,0,,0]′表示目标运动中出现的过程噪声；,+1表示状态转移矩阵，且

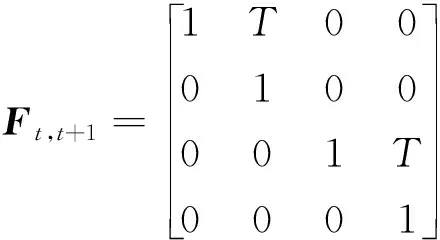
(2)

雷达对目标的量测只能过程得到目标的径向距离和方位角数据，量测方程为

+1=()+

(3)

式中：=[,]′表示量测误差矩阵；=[,]′表示目标在时刻的量测向量，(·)表示量测过程，、分别表示目标的径向距离和方位角，即

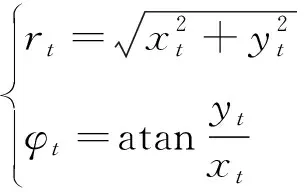
(4)

平面中，量测点的回波能量为

(5)

式中：为雷达发射功率；为天线增益；为目标的雷达散射截面积；为发射电磁波波长。考虑到目标存在起伏，则雷达接收到量测点的回波能量为

(6)

式中：为均值为0服从高斯分布的参数，用于描述能量起伏性。

2 算法原理

PT-TBD算法主要分为4个步骤，首先将目标量测点以规格化后的径向距离-时间坐标表示；其次按照平行线坐标变换规则，完成同坐标系下的点到线的转化；接着网格化线段分布范围，进行双重积累；最后提取峰值，并对回溯的航迹进行约束从而得到最终结果。算法流程如图1所示。

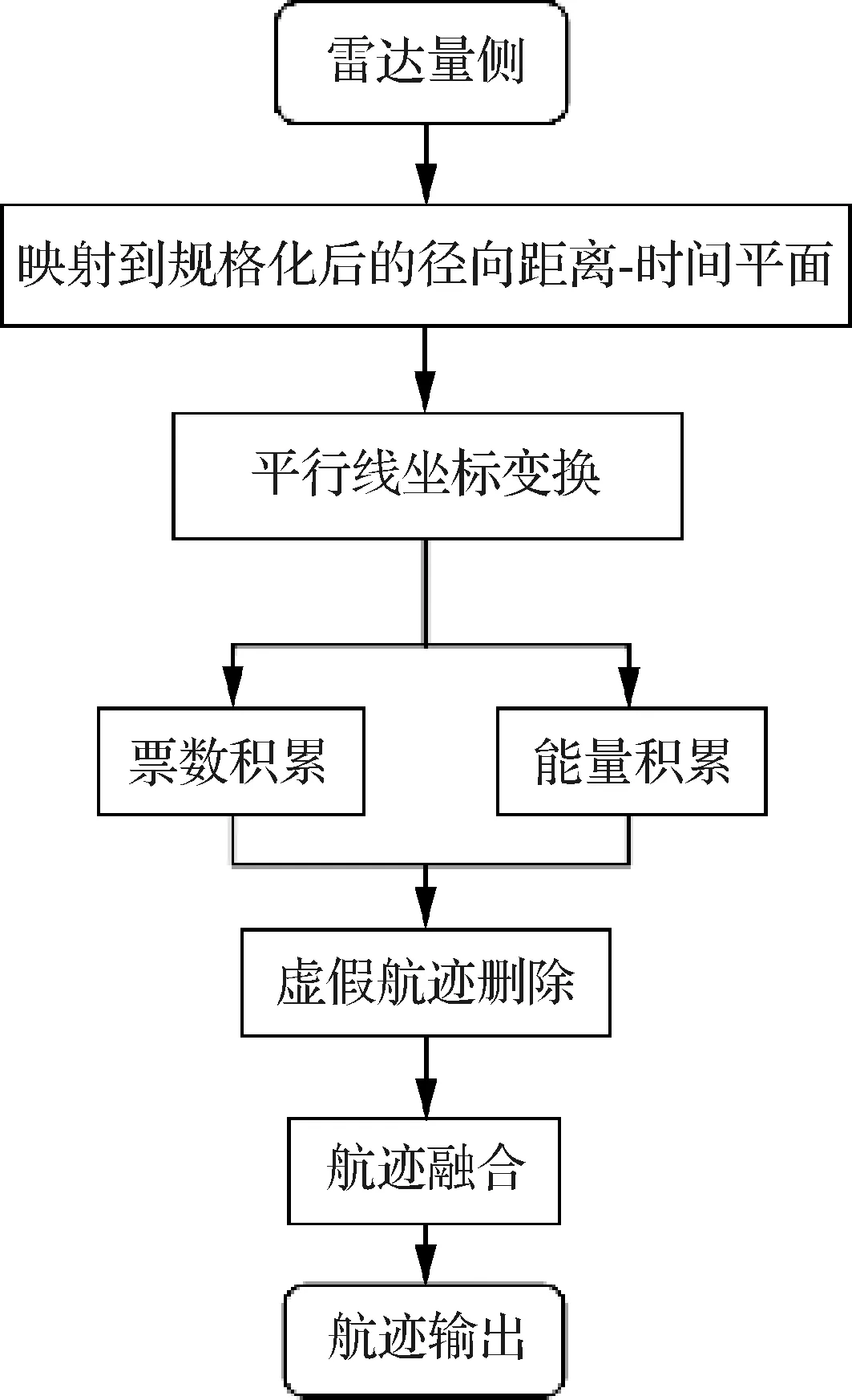
图1 PT-TBD算法流程图Fig.1 Flowchart of PT-TBD algorithm

2.1 平行线坐标变换

传统的HT-TBD算法，是将平面中的点坐标按照Hough变换将量测点变为参数平面中的曲线。本文提出的平行线坐标变换检测前跟踪方法，与其有着相似之处。对于空间中某点(,)，在相同的-二维笛卡尔平面上绘制2条垂直于横坐标轴且到轴距离相等的对称平行直线，设为和，直线上的点横坐标均为-， 直线上的点横坐标均为，2线之间距离为2。在直线上找到纵坐标为-的点(-, -)，在直线上找到纵坐标为的点(,)，在轴上找到纵坐标为的点(0,)。分别连接(-,-)和(0,)、连接(,)和(0,)形成2条新的线段，2条线段所在直线的方程分别为

(7)

对-二维笛卡尔平面上的所有点进行变换后，完成点到线的转换。会发现，原先处于一条直线=+上的2点必会在新坐标系内交于一点(,)，当>0时，其坐标为

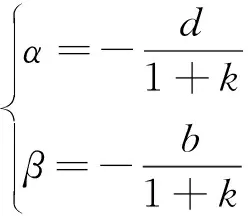
(8)

当<0时，其坐标为

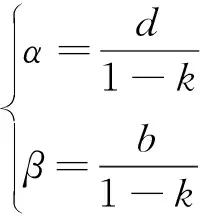
(9)

当=0时，其坐标为(0,)。属于>0和<0直线的量测点，其平行线坐标变换规则如图2所示。

图2 平行线坐标变换示意图Fig.2 Schematic diagram of parallel-line-coordinate transformation

图2中，点～为-二维坐标系上的原始点，点′～′为-二维坐标系上原始点以轴为中心的对称点，点～属于一条直线，在平行线坐标系下变成6条线段后交于绿色五角星点；点～属于另一条直线，在平行线坐标系下变成6条线段后交于红色五角星点。

2.2 PT-TBD算法

2.2.1 非相参积累

非相参积累完成后，会有一些目标航迹周围的虚假航迹积累能量超过积累门限，且量测点的-坐标多伴随较大的横向误差。解决这些问题的一般方法是先将量测点坐标映射到径向距离-时间坐标，后续根据先验信息设置选通条件在-坐标系下进行约束。同时，由于量测时间数量级远小于目标径向距离，如果不进行处理将出现全部直线高度聚集且斜率趋近无穷，因此需进行坐标规格化，公式为

(10)

(,)→(,·)

(11)

关于参数的选取，其基本原则是保证两平行线之间距离与点变换过来的线段在两平行线之间变化的范围处于一个数量级，由于直线与直线上选取点的纵坐标分别是原坐标系下点纵坐标的负值与正值，轴上选取点的纵坐标是原坐标系下点的横坐标，因此平行线坐标系所有线段的纵向变化范围为

=max(max(),max(·))-min(-)

(12)

则令平行线间距=05。

此时，变换后线段的分布范围为一个正方形，分割正方形为×个网格，对每个网格进行线段所代表量测点的能量和票数的带值积累。例如，时刻的点(,)所代表直线穿过网格(,)，其能量为，建立能量积累矩阵和票数积累矩阵，则当满足：

(13)

或者

科思创中国区总裁盛秉勇（Bjoern Skogum）表示：“可持续发展是科思创的核心战略支柱之一，中国正对化工行业进行大规模整治重组，以实现可持续发展。在这一背景下成为行业榜样意义重大。作为一家跨国企业，科思创将继续为中国化工行业的可持续发展作贡献，到2025年将生产每吨产品产生的二氧化碳排放较2005年降低50%，利用我们全球化的专业知识让中国更美好。”

(14)

对2个积累矩阵进行积累，积累过程中，为充分利用时间信息，更有效地检测航迹，假设该单元时刻有个的直线穿过，只取能量最大值进行积累

(15)

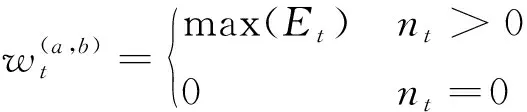
(16)

(17)

接着设置能量积累门限和票数积累门限，将满足2个积累门限的单元内包含量测点输出，得到最终结果。

采用2种积累方式的好处是当空间中存在多个回波能量不同的航迹时，可能会出现回波能量差异较大的现象，一般为保证检测概率会降低积累门限，但同时会引入大量虚假航迹，此时采用票数积累将会把其中包含的量测点总数很少但存在个别目标量测点的虚假航迹滤除掉。

2.2.2 虚假航迹删除

由于积累后存在峰值簇拥现象，与真实目标航迹所在单元相邻的单元积累值仍较高，导致其构成虚假航迹被错误地提取出。但之前采用的是量测点的径向距离-时间坐标，为此处的虚假航迹删除提供了便利。

设所探测的目标飞行速度可能达到的最大值为，可能达到的最小值为，目标相邻的2条帧间航迹构成转向角最大值不超过。设、、分别代表峰值提取后，同一条航迹中时刻为、和的量测点，则真实航迹量测点需满足:

(18)

2.2.3 航迹融合

完成虚假航迹删除后，仍存在真实目标被检测出多个航迹的现象，表现为部分航迹中存在虚假量测点，可通过航迹融合解决。即在跟踪帧数为时，当2条航迹中有个量测点重合时，对2条航迹中相同时刻不同的量测点，删除能量小的量测点并合并2条航迹：

(19)

2.3 算法理论分析

为进一步探寻PT-TBD算法对HT-TBD算法的优越性，本文作者做了更多的工作。

PT-TBD算法与HT-TBD算法均属于基于投影变换的检测前跟踪算法，最终目的都是为实现目标航迹的有效积累，尽可能地将所有目标量测点的能量积累到一个单元中，避免出现积累损失。此时，能够将更多目标量测点所变直线聚集到一个单元内进行积累的算法，积累损失也就越小。

积累损失现象，由2个原因共同造成：

量测误差的存在。目标航迹不是一条严格的直线而是分段折线，完成点到线的变换后各分段折线所代表交点无法落到一个单元格内。

离散化直(曲)线造成的纵向偏差。实际算法在分单元积累时是将量测点所变直线或曲线进行采样处理，积累峰值一般不会恰好选到交点而是选到交点邻域内的点，当直线或曲线纵向差值超过单元边长就会使采样点落到不同的单元。

假设-二维平面中的存在3个位于同一条直线的量测点：(,)、(,)和(,)，且设>>>0，>>>0。其中，量测点(,)产生量测误差(Δ,Δ)，导致接收到的位置坐标为(+Δ,+Δ)。

对于原因1：

当不产生量测误差时，采用Hough变换所变曲线的交点位置坐标(,)中：

(20)

量测点(,)产生量测误差后，分段折线交点位置的横坐标分别为

(21)

使得在平面上原本应当落于同一个单元格内的交点产生的横向偏差为

=-=

(22)

同理，当不产生量测误差时，采用平行线坐标变换所变直线的交点位置坐标(,)中：

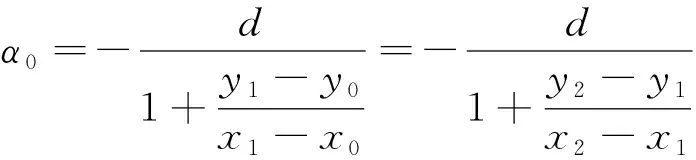
(23)

式中：

=05(max(max(),max())-min(-))

(24)

量测点(,)产生量测误差后，分段折线交点位置的横坐标变为

(25)

使得在平面上原本应当落于同一个单元格内的交点产生的横向偏差为

=-=

(26)

对于原因2：

此处只考虑产生量测误差的量测点(,)和前一个量测点(,)，当采用Hough变换时，2个量测点所变曲线为

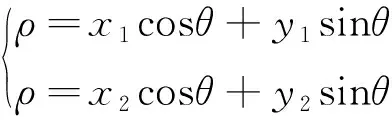
(27)

当取同一值时，二者纵向相差

Δ=(-)cos+(-)sin

(28)

设2条Hough变换后曲线应相交于(,)，计算2条曲线纵向的差值随变量～的距离增大的变化公式，并将纵向距离差值为0的点移到坐标零点，结果为

=

|(-)cos(+)+(-)sin(+)|=

(29)

并且：

(30)

同理，当采用平行线坐标变换时，2个量测点所变直线按照式(7)进行变换，由于目标的轴向速度和轴向速度均大于0，则量测点所变直线在负半平面存在交点，直线公式为

(31)

当取同一值时，二者相差：

(32)

设2条平行线坐标变换后直线应相交于(,)，计算2条直线纵向的差值随变量离的距离增大的变化公式，并将直线以轴为对称轴翻折至正半平面，再将纵向距离差值为0的点移到坐标零点，结果为

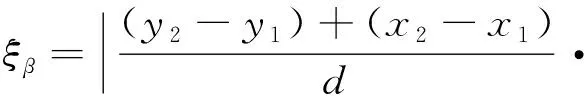
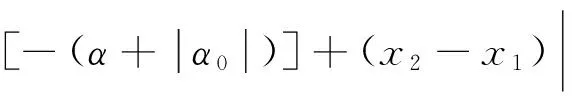
(33)

此时，式(29)和式(33)均是过零点函数，将式(22) 和式(26)分别代入式(29)和式(33)，求此时产生的纵向误差得：

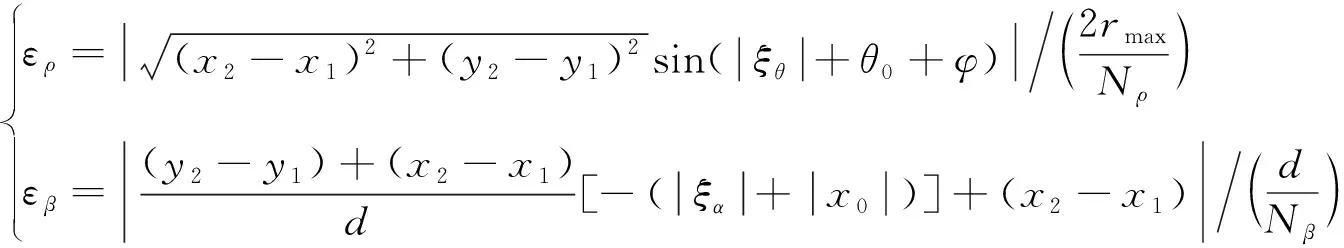
(34)

通过对比在相同量测误差Δ和Δ下和的值，即可对比二者产生的积累损失大小。

3 仿真验证

3.1 算法仿真

设-二维笛卡尔平面中包含2个目标航迹，目标1的初始位置为(2 km,4 km)，运动速度为(100 m/s,80 m/s)；目标2的初始位置为(3 km,3.8 km)，运动速度为(150 m/s,-120 m/s)。量测范围内存在杂波，其数目服从每帧50个的泊松分布，总体信杂比为SCR=6 dB。雷达位于坐标原点，径向距离量测误差为=20 m，方位角量测误差为=0.01°。则雷达量测二维平面图如图3所示。

图3 雷达量测Fig.3 Radar measurements

为减小雷达的量测误差对结果的影响，并便于后续筛选航迹，将接收到的量测点映射到径向距离-时间平面，并进行坐标规格化，规格化系数为=95315，如图4所示。

图4 r-t坐标系下雷达量测Fig.4 Radar measurements in r-t coordinate system

将坐标按照平行线坐标变换完成点到线的转换下，计算得到=6 673 m，得到结果如图5所示。

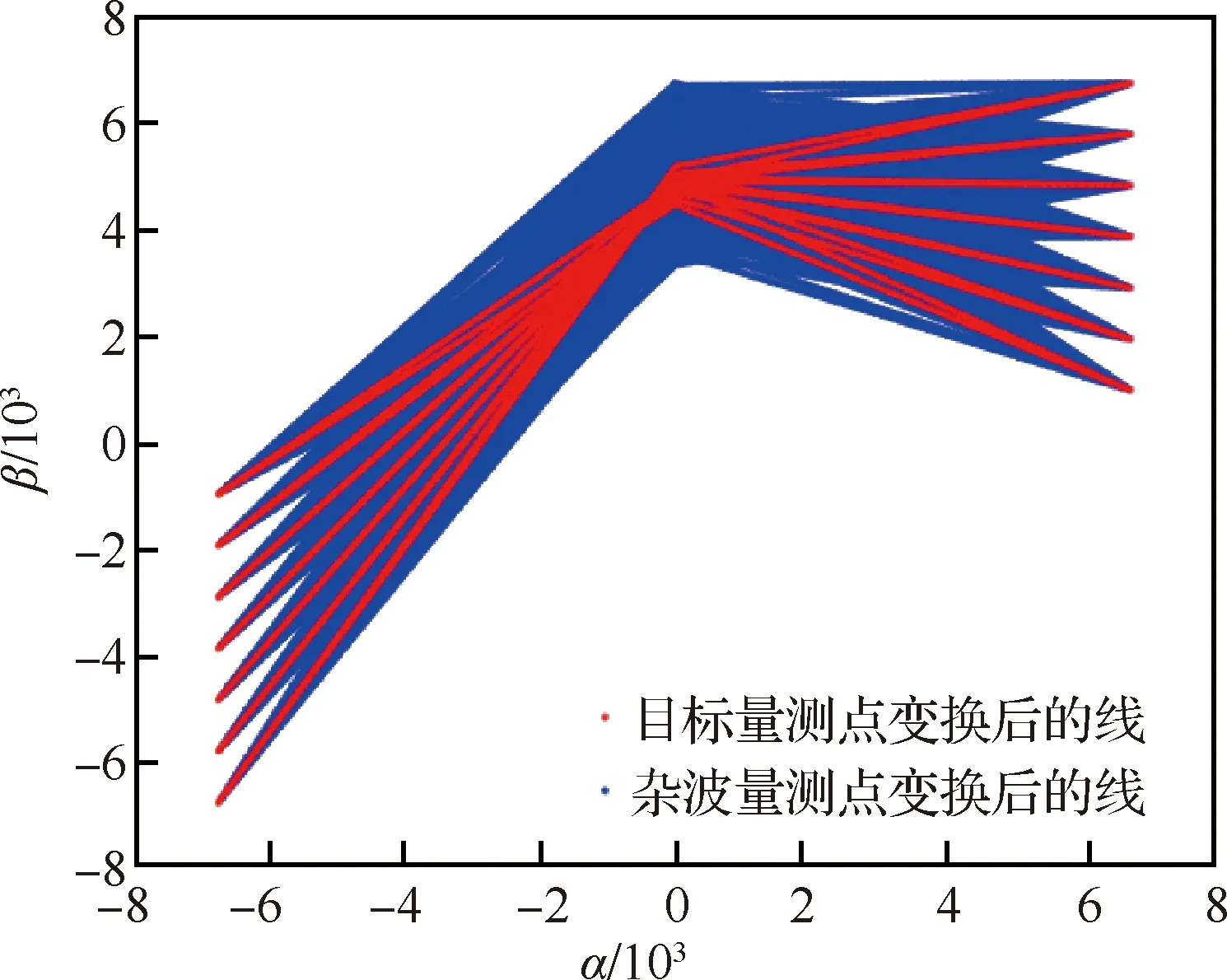
图5 平行线坐标变换结果Fig.5 Parallel-line-coordinate transformation result

设平行线坐标分割段数为=360，将变换后平面内的线段分布范围分割为360×360个单元格，建立票数积累矩阵(360,360)和能量积累矩阵(360,360)，并按照式(13)～式(17)对每个网格内通过的曲线做票数积累和能量积累，得到结果如图6和图7所示。

图6 票数积累Fig.6 Accumulation of votes

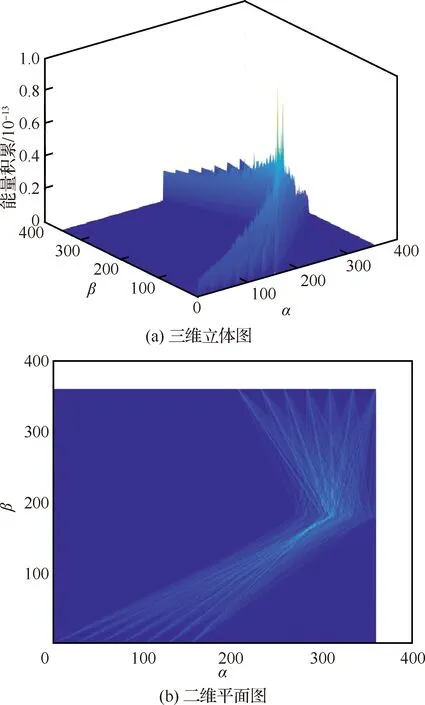
图7 能量积累图Fig.7 Accumulation of energy

由于积累帧数为7帧，设置票数积累门限为4，能量积累门限为积累最大值的0.7倍，提取满足2个积累门限的网格内量测点组成航迹，得到结果如图8所示。

图8 门限提取后输出航迹Fig.8 Track output after threshold extraction

根据先验信息以及雷达量测误差，设置速度选通条件为=200 m/s，=70 m/s，设角度约束条件为=90°。经过航迹约束和航迹融合后的最终检测结果如图9所示。

3.2 有效性测试

为进一步测试本文算法对微弱目标的有效检测，将通过不同信杂比下目标的检测概率、虚假航迹率和不同杂波密度下的运行时间进行说明。

3.2.1 检测概率

设检测概率为，设某次仿真中，某条输出航迹有帧量测点与真实目标航迹重合，当采用4/7逻辑时，令是否检测到目标的判断系数为，即

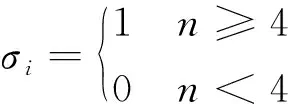
(35)

则次蒙特卡洛仿真中，目标的检测概率为

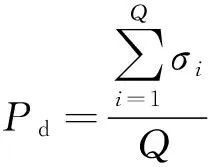
(36)

在信杂比SCR为0～10 dB条件下进行=300次的蒙特卡洛仿真，分别使用HT-TBD算法和PT-TBD算法计算2个目标各自的检测概率以及全部目标的检测概率，结果如图10所示。

图9 最终输出航迹Fig.9 Final output track

由图10可以看出，2个目标各自的检测概率以及2个目标全部被检测到的概率均随信杂比的升高而升高。当信杂比超过3 dB时，2个目标各自的检测概率以及全部目标的检测概率均可达到90%，证明本文算法能够对目标进行有效检测。但同时发现，PT-TBD算法的检测概率优于HT-TBD算法，尤其是在SCR<4 dB时。

图10 2个目标各自被检测的概率和全部 被检测的概率Fig.10 Probability of detection of each target and both targets

3.2.2 虚假航迹率

设虚假航迹率为，则

(37)

式中：为第次仿真检测到的虚假航迹数；表示第次仿真中检测到的总航迹数。同样在信杂比为0～10 dB条件下进行=100次的蒙特卡洛仿真，计算不同信杂比下算法的虚假航迹率，结果如图11所示。

由图11得出，2种算法的虚假航迹率均随信杂比的升高而下降。对于本文PT-TBD算法，当SCR<2 dB时，虚假航迹率超过90%，说明高回波能量的杂波量测点干扰了雷达对目标的正常检测；当SCR>9 dB时，虚假航迹率小于20%。总体上看，本文PT-TBD算法虚假航迹率与HT-TBD算法相近。

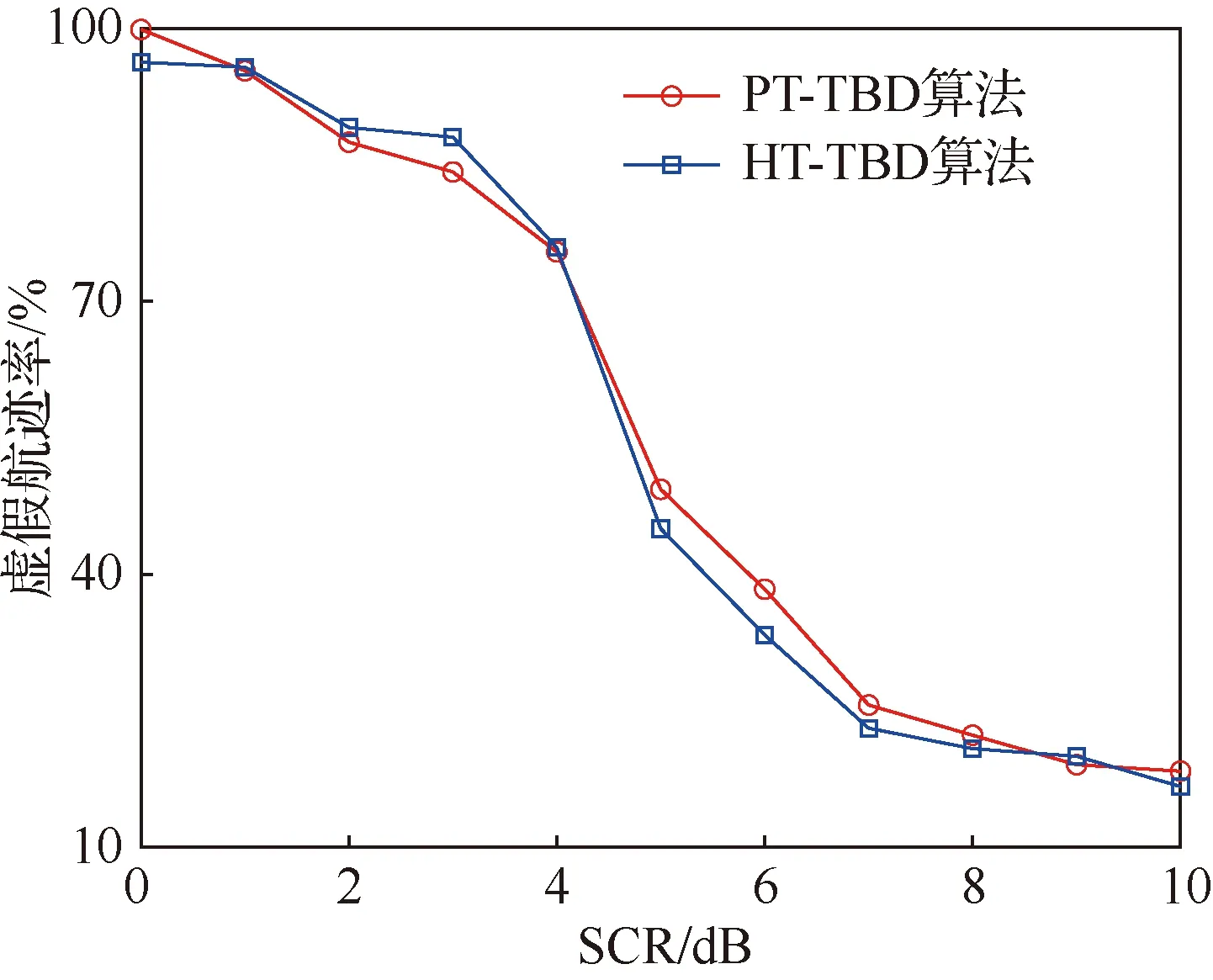
图11 不同算法下的虚假航迹率Fig.11 False track rate with different algorithms

3.2.3 运行时间

改变每帧杂波密度，观察算法运行时间，由于杂波密度变化不是等差数列，结果如表1所示。

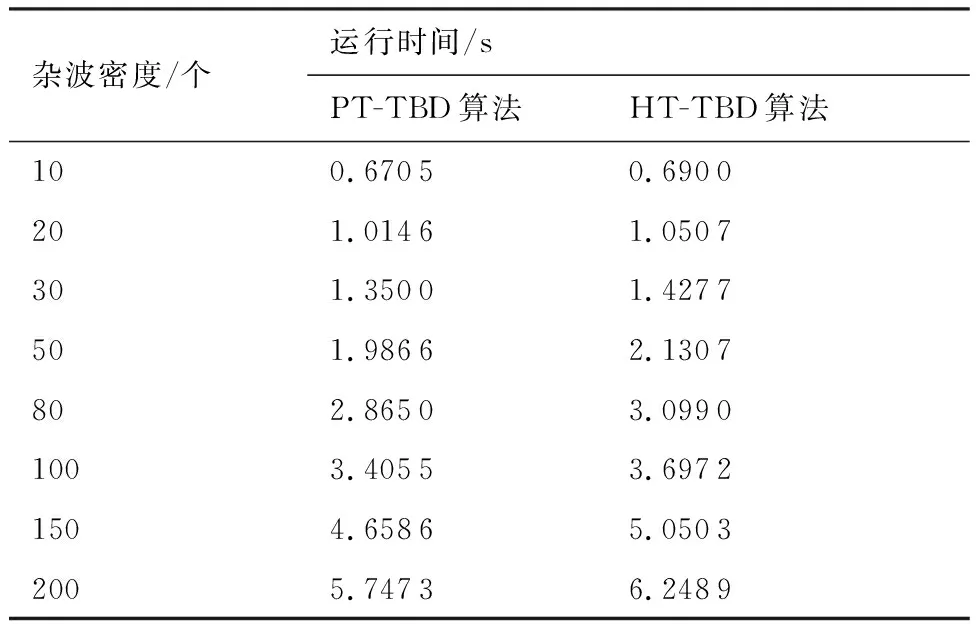
表1 不同杂波密度下的运行时间Table 1 Running time with different clutter density

由表1所示，在不同杂波密度下，本文PT-TBD算法运行时间比修正HT-TBD算法运行时间更短，且时间减少效果随着杂波密度的升高而提升。也证明文献[9]中所提的平行线坐标变换属于线性变换，计算量要小于Hough变换的结论。

3.3 算法仿真分析

按照3.1节参数设置中目标1的前2个量测点设置，如表2所示。

表2 参数设置Table 2 Parameter settings

按照式(34)分别计算相同的2个点经Hough变换和平行线坐标变换后，随着离交点的横坐标距离增长使得2线纵向差值的变化曲线如图12所示。

图12 纵向偏差值变化图Fig.12 Chart of variation of longitudinal deviation value

由图12可以看出，采用Hough变换后的2线纵向差值呈现非线性变化；而采用平行线坐标变换后的2线纵向差值呈现线性变化。同时发现，当横坐标距离交点位置所跨单元格数小于145个时，在相同的横向跨单元数目下，经Hough变换后的纵向差值大于经平行线坐标变换后的纵向差值。

但考虑到即使是相同的量测误差下，2种算法产生的横向差值也存在差别，因此需要继续计算。设量测点(,)在-二维平面的2个维度产生的量测误差Δ与Δ均从-50 m以1 m为公差增到50 m，计算2种变换产生的横向跨单元格数目如图13所示。

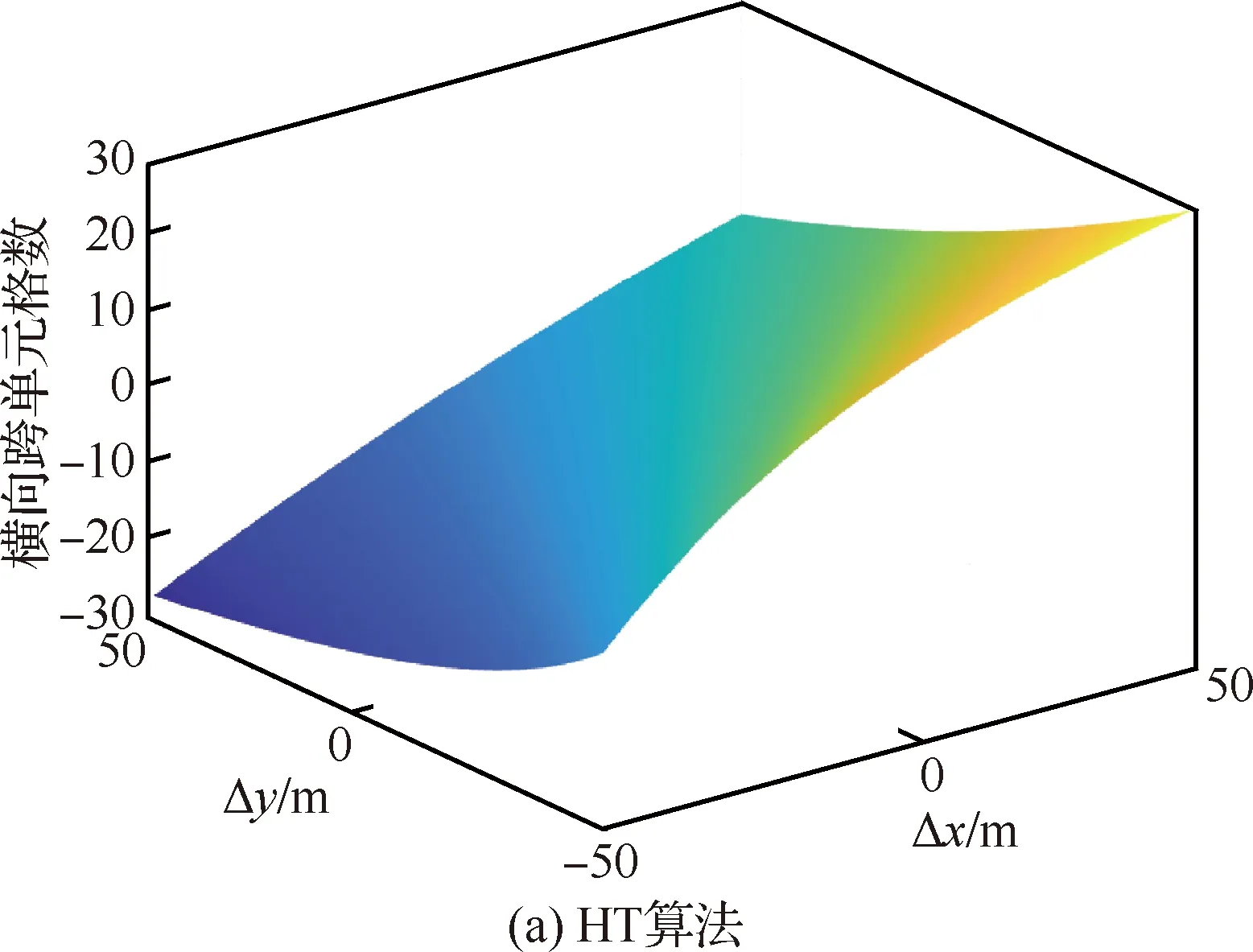
图13 2种算法横向跨单元格数目Fig.13 Number of horizontal cross-cells of two algorithms

此时的结果表现为，在产生相同量测误差的情况下，2种算法产生了相同趋势的横向跨单元格数，但HT算法产生的横向跨单元格数要少于PT算法产生的横向跨单元格数。再将各自量测误差情况下产生的横向跨单元格数代入式(34)中计算其纵向产生的偏差，得到结果如图14所示。

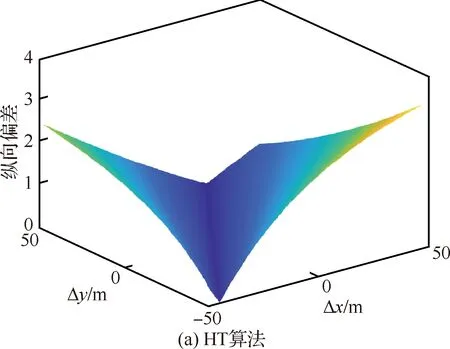
图14 2种算法纵向偏差Fig.14 Longitudinal deviation of two algorithms

2种算法纵向偏差的差值图如图15所示。由结果可以看出，虽然在相同量测误差下，HT算法比PT算法产生了更小的横向偏差，但当代入式(34)后，HT算法总体上纵向偏差更大。由于在仿真计算时，直(曲)线采样是按照横向等间隔采样，且实际中雷达存在量测误差，因此在纵向产生更大偏差的HT-TBD算法将产生比PT-TBD算法更大的积累损失。

图15 HT算法比PT算法纵向偏差的差值Fig.15 Difference longitudinal deviation of HT algorithm than that of PT algorithm

再按照3.1节设置的场景参数，假设只有目标1存在，在不同信杂比条件下同时进行平行线坐标变换和Hough变换，将2种变换后的平面均分割为360×360个单元并进行能量积累。在=300次的蒙特卡洛仿真中，PT-TBD算法与HT-TBD算法能量积累的最大值与目标航迹整体能量积累损失率为

(38)

2种算法不同信杂比条件下的积累损失率如图16所示。再通过相同环境设置，观察2种方式能量积累的峰值大小比较结果如图17所示。

由图16和图17明显看出，2种算法在不同信杂比下均存在一定程度的积累损失，PT-TBD算法的平均积累损失率为1.68%，HT-TBD算法的平均积累损失率为2.96%，说明PT-TBD算法的积累损失要小于HT-TBD算法。由于探测范围内只设置单个目标且信杂比均不低于0 dB，因此理想情况下能量积累最大值与目标航迹能量积累值应当相同，出现积累结果不等的原因是当目标不以严格直线轨迹运动时，量测点变换成直线后不会严格交于一点，导致部分量测点无法正常积累。

图16 不同信杂比条件下的积累损失率Fig.16 Cumulative loss rate with different SCR

图17 不同信杂比条件下的积累峰值大小对比Fig.17 Comparison of cumulative peak size with different SCR

由图17可看出，3种情况所占比重在不同信杂比条件下大致相似。经计算得，有64.22%的概率2种算法的能量积累峰值相同，有27.18%的概率PT-TBD算法能量积累峰值更大，只有8.6%的概率HT-TBD算法最大能量积累峰值更大。

平行线坐标变换与Hough变换均是实现点到线的变换，不同的是，平行线坐标变换是实现点到直线的变换，而Hough变换是实现点到曲线的变换。当存在量测误差时，曲线“凸”的性质加大了曲线落向参数平面内其他单元的可能，使得HT-TBD算法产生更大的积累损失。

图18是沿直线飞行目标的3帧量测点分别采用平行线坐标变换和Hough变换的结果，其中量测的距离误差为=20 m，方位角误差为=001°。显然，PT-TBD算法中存在有3条直线穿过的单元，而HT-TBD算法中不存在有3条直线穿过的单元，发生了积累损失。

图18 2种算法量测点变换线情况Fig.18 Conversion of measuring point to line in two algorithm

综上所述，PT-TBD算法相对于HT-TBD算法的优点和原因是：

1) 检测概率更高，积累损失更小，对微弱目标的检测性能更好。具体原因是在网格化参数平面时，Hough变换所生成的曲线将比平行线坐标变换所生成的直线有更大的可能性落入不同的单元格内，造成更大的积累损失，从而降低目标的检测概率。

2) 运算时间更短。具体原因是平行线坐标变换为线性变换，Hough变换是非线性变换。

算法仿真分析是按照算法理论分析中的假设进行参设设置，即认为目标轨迹方程的斜率>0。要特别说明的是，当目标轨迹方程的斜率≤0时结论仍然正确。

4 结 论

1) 平行线坐标变换为线性变换，Hough变换为非线性变换，导致PT-TBD算法运算时间比HT-TBD算法更短。

2) 在相同量测误差和参数平面分割数目设置下，PT-TBD算法平均积累损失率为1.68%，HT-TBD算法的平均积累损失率为2.96%。说明PT-TBD算法积累损失更小从而拥有更高的检测概率。

3)PT-TBD算法与HT-TBD算法的检测概率均随信杂比的升高而升高，但总体上看，PT-TBD算法的检测概率要高于HT-TBD算法，且在信杂比小于4 dB时较为明显。

4) 采用航迹修正步骤后，PT-TBD算法与HT-TBD算法产生的虚假航迹数相近。

5) PT-TBD算法仍属于基于投影变换的检测前跟踪算法，对沿直线运动的目标检测性能好，但不可避免的在面对机动目标时，检测性能下降，仍有局限性。未来将会研究针对沿非直线运动目标的改进PT-TBD算法。