大学数学中基于学习动机理论的课程思政
赵 阳, 徐厚宝, 曹春雷
(北京理工大学数学与统计学院,北京 100081)
1 引 言
课程思政可以理解为:挖掘专业课.通识课等课程中的思想政治教育元素,并有机融入课程教学中,实现全员育人、全程育人、全方位育人.2020年5月,教育部印发的《高等学校课程思政建设指导纲要》深入地阐述了课程思政的重要意义,本质内涵和实践举措,特别是为各专业课程思政的核心内容和科学设计提供了理论和方法指导.众多学者围绕课程思政或阐释理论方法或结合专业应用到实践中[1-12].课程思政的落地落实、见功见效不仅需要教师提高自身素质,在融入思政元素时做到如盐入水,更要促使思政元素内化于学生的心中,所以在整个教学过程中要时时关注学生的情感动态,从人性维度、志趣情怀方面加以引导.
教育心理学认为,学习成功需要具备认知、情感和元认知三个条件[13],这里主要关注情感部分——学习动机.学习动机是指激发,维持学习活动,并致使行为朝向学习目标的一种内在过程或内部心理状态[14],学生的学习动机是素质教育的重要组成部分,参考文献[15]认为,动机是学生在学校中成功或失败的最强大的决定因素之一.对于工科学生必修的大学数学的三门课程:微积分,概率统计,线性代数来说,学习动机尤其重要,因为数学课程内容抽象枯燥,逻辑严密难懂,学生往往学习积极性低,效果差,因此在教学策略中利用当代的学习动机理论来促进学习是十分必要的.
鉴于课程思政和学习动机共同聚焦于学生的情感,本文尝试基于学习动机理论视角构建课程思政.当代学习动机理论十分丰富,包含成长动机理论、期望-价值理论、归因理论、社会认知理论、目标导向理论、自我决定理论等[16-17],这些理论之间有交叉也有区别,能力、价值、归因以及个体与学习环境之间的互动等是这些理论中反复出现的主题.
结合大学数学的课程思政探讨已取得不少成效[6-12], 参考文献[6]探讨了在大学数学课堂教学中落实课程思政的有效路径,参考文献[7]构建了大学数学教学与课程思政融合发展的途径,参考文献[8]基于疫情期间的思政素材,为微积分中的“课程思政”提供了思路,参考文献[9]探索了高等数学课程中中如何实现从思政课程到课程思政的转化,参考文献[10]基于传染病模型研究了如何在数学模型课程教学中渗透“课程思政”,参考文献[11]从哲学视角给出了高等数学“课程思政”过程中哲学意识的渗透点及路径,参考文献[12]基于数学文化探讨了提高数学文化教育的价值引领方式及作用.但基于动机理论的视角引入思政的研究论文并不多,主要集中在文科或中学范围内,理科方面的相关论文没有见到.例如:参考文献[18]中探讨了基于ARCS理论开展高校网络思政教育的思路,参考文献[19]中基于归因理论探讨了运用韦纳归因理论来激发初中生的学习动机.本文将依托动机理论的几种情形构建大学数学中的课程思政.
2 基于成长动机论的课程思政
心理学家马斯洛的成长动机论是基于人本主义的动机观,他认为满足需要是个体发展最重要的原则,提出了包含五个水平的需要层次说,这五个水平从低到高依次为:生理的需要,安全的需要,归属与爱的需要,尊重的需要,自我实现的需要,前四种为缺失性需要,最后一种为成长性需要,只有满足低层次的需要,才会产生高层次的需要[17].
目前大学数学课堂基本上是大班授课,教师与学生之间的关系比较疏离,教师的角色权威成分重,亲和力不足,许多学生担心受到教师的批评,同学的嘲笑,在整个课程中始终沉默,课堂氛围僵化,而数学课本身的抽象枯燥更加重了僵化状态,这使得学生难以表达自己的问题,不能进入真正的深度学习[20].
基于成长动机理论,教师需要构建一种相互倾听,相互成长,相互信任的安全氛围.首先教师应让自己被听见.教师可以介绍自己最近的学习状态,让学生感受到教师和他们一样都是学习者,减弱权威感,拉近和学生的距离,还可潜移默化地传达终身学习的理念.教师可以公开自己的教学策略,教学内容做了怎样的改进,教学方法做了怎样的调整,让学生认识到课堂不是一成不变的,感受到教师对课堂教学的用心和尊重.其次教师应让学生被听见.教师可以每隔一段时间来让学生来发表对课堂教学策略的感受,反思这段时间的收获和不足,需要怎样的帮助等.教师可使用形成性测试发现“学困生”,主动与学生对话,探讨解决方法.例如,笔者在概率课堂上的第一节课介绍笔者自己这段时间的学习情况:学习了两门MOOC(人是如何学习的和教学动画制作).并说明这门课的教学每年作了哪些改进:引入同伴教学(基于国内外的题目,建立课堂测试题,分两次答题,第一次独立答题,第二次合作答题),增加了自己制作的情景动画等,课中利用雨课堂使用了同伴教学测试,每次课后软件就会推送出学业警示的学生,可以就本次课内容进行询问,了解情况,让其自选部分内容下次来讲解.课后教师从多种渠道倾听到学生的声音(发布李克特量表问卷、问答问卷等),部分反馈见表1,据此进一步改变教学设计,又让自己被看见,形成良性循环.最后教师应多引导学生之间进行合作学习,形成良好的积极互赖关系.师生之间,生生之间相互倾听增进了彼此之间的相互信任,促进了相互成长.教师和学生都是学习者和创造者,共同打造出一个融合的课堂.

表1 部分学生反馈
3 基于期望-价值理论的课程思政
在期望-价值理论中,学习动机是成功期望和任务价值的函数.期望是个体对自己成功完成任务能力的信念和判断,个体预期达到目标的可能性越大,个体的学习动机也越强.价值指的是个人对从事任务的原因的信念,又可分为内在价值(给定的主题是有趣或愉快的)、外在价值(主题具有实用性,或者是未来目标所需的)、成就价值(完成任务本身就是学习者自我概念的肯定)、消耗成本[10,13].成功期望和任务价值这两个主要变量影响学习动机.
成功的期望值受到目标、自我概念和任务难度等因素的影响.首先,教师可以结合课程内容,挖掘增强 “四个自信” 的思政元素,激发学生的爱国之情与自豪感,勉励学生树立为中华民族复兴而奋斗的远大理想.例如,概率统计课程中数学期望和方差分别反映了随机变量取值的集中和离散程度,作为此概念的引例可播放习近平总书记的扶贫足迹视频,通过扶贫可减少贫富差距,提高平均生活水平,这正是期望方差的释义.在此可展现扶贫攻坚的成就及国际评价,体现我国社会主义制度的优越性,促使学生实现政治认同、思想认同、情感认同,这样才能树立为中国特色社会主义奋斗的目标.其次,在课程内帮助学生设置中等难度的任务,让学生体会到成功完成目标的价值感受.例如,在概率和微积分的同伴教学测试中需要根据往年学生的答题情况和学生所在专业的特点及时调整题目,增强学生获得成功的信心和期望,提高学业自我概念水平.
基于价值的四个因素,教师可创设许多情景,引入有趣的、冲突的、前沿的、实用的案例.例如,微积分中向量理论可用于新闻的分类[21];一个抽象的关于e的重要极限关联着财务自由问题(笔者制作了相关动画,可来信索取);由六角柱状体组成的蜜蜂蜂巢结构十分巧妙,其中的设计理念可以利用极值理论来建模[22],这个问题是华罗庚为普及数学而写的,借此也可介绍华罗庚自学成才的故事,进一步突出设立期望目标的重要性.概率统计本身就是一门充满辩证法的课程,例如笔者基于贝叶斯公式制作了体现认知冲突的阳性与癌症动画;基于相关系数制作了澄清相关与因果之间的误解,正确解读数据的动画;基于数学期望的应用制作了结合当前新冠肺炎混合检测策略的动画;基于大数定律制作了体现探索精神的动画;采用最新的研究成果——2019年发在《自然神经科学》上的文章:同步脑回路节律的刺激可以改善老年人工作记忆——来探讨假设检验的意义.另外,在解决问题时,引导学生进行知识众筹,体会个人努力的价值.
4 基于归因理论的课程思政
归因理论强调学习者为解释结果而归纳的原因.个体通常把事情成败归结为如下六个原因:能力、努力程度、任务难度、运气、身心状况、外界环境,这六项因素可划分为三个维度:(i)因素来源,如能力、努力和身心状况属于内控,其他三项属于外控;(ii)稳定性,如能力与任务难度通常认为是稳定的;(iii)可控性,如努力程度是可控的.归因直接影响学生对未来成功的期望和学生的情感体验.如果学生把成功归因于运气时,学生可能就不会对结果感到自豪与满意,也没有强烈的学习动机.归因理论的启示有:归因要可信;应把成功归因于能力和努力的共同作用,失败归因于努力不够[12].教师应在教学过程对学生提供反馈时帮助学生形成准确、积极的归因.
基于归因理论,结合数学课程特点可引入许多思政元素,强调努力的重要性.例如,概率统计中的二项分布理论证明了小概率事件虽不易发生,但重复次数多了,就成大概率事件,可以引申为有志者事竟成,成功的概率虽然很小,但坚持不懈的努力终会走向成功,进而可介绍诺贝尔生理学或医学奖得主、中国科学家屠呦呦历经无数次试验和失败从2000多种中草药中找到了抗疟新药青蒿素,借此勉励学生要刻意锻炼出坚忍不拔的优秀品质.中心极限定理是后面要学的内容,体现了量变到质变的变化过程,质量互变规律是唯物辩证法的基本规律,“量变是质变的必要准备,质变是量变的必然结果,质变不仅可以完成量变,而且为新的量变开辟道路”[23],进一步强化坚持不懈的努力终会发生质变,实现理想.
归因理论中往往把能力视为稳定的,难以改变的,如果学生很努力,但仍然失败了,因此归因为自己能力弱,显然不利于进一步的学习.教师应辅助学生培养能力的增长观,让他们相信能力是可以经过刻意训练得到提升.例如,在学习韦恩图时,因为韦恩图的直观性,学生就会在解决问题时全用韦恩图来处理,因而就无法进行下去,笔者引导学生先放弃韦恩图,直接用推理的方法来尝试,反复练习就发展出抽象思维能力.又如学生往往喜欢套用模型做题,一维的题目会做了,不能迁移到二维中去,笔者为此利用最近发展区理论设置了预习题目,从即将要学的新内容中构建出一些可以利用学生现有知识能够解决的问题,发展学生的迁移能力.培养学生的能力增长观可以使得学生更具有前进的动力.
5 应用成效
在2020年秋季和2021年春季的课程上实施了本文所述方法,取得了一定的成效.2020年秋季作者教授两个概率统计班:一班和二班,两个班使用相同的情景案例,思政案例及课堂测试题,不同之处是一班使用课堂测试题时增加了同伴讨论及在每一章里增设了翻转课堂.最后期末考试成绩表现出一定的差异.一班的平均成绩79.50,标准差为13.73,二班平均成绩为76.05,标准差为16.37,一班平均成绩更高,方差更小(见表2).表3是两班成绩的T检验效果(双侧检验),p=0.073,可以说具有边缘显著性,或者说在显著性水平10%下具有显著性,表明一班成绩略优于二班成绩.这两个班的教学方法只差了同伴讨论这一项,成绩差距不是特别突出.

表2 两班概率成绩统计
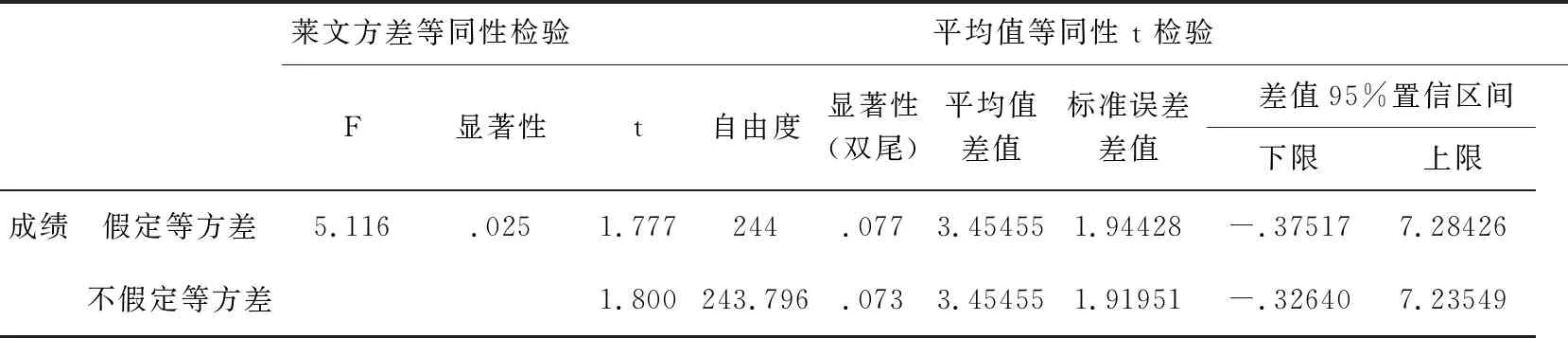
表3 两班概率成绩的T检验
2021年春季笔者与另外一个老师分别教授两个文科班的微积分II课程,在笔者的课程上实施同样的教学策略,另一位老师仍用传统的讲授方法,两班教学策略差异较大,最后的期末成绩也呈现了比较大的差异.笔者所教的班命名为一班,另一位老师所教班为二班.表4显示一班的平均成绩76.59,标准差为10.84,二班平均成绩为72.17,标准差为15.17,一班的平均成绩明显更高,方差更小.表5是两班成绩的T检验效果,p=0.11,在显著性水平0.05下未表现显著差异.因为样本量影响统计检验力,样本量越大,检验力越大,更易得到显著性.微积分课程中学生人数比较少,影响显著性结果的出现,但均值的差异比概率统计课程中均值差异大,因此来对比二者的效应大小,效应是对均值差异的标准化测量.采用cohen’s d公式计算得到概率统计课程中不同教学策略下的效应为0.23,微积分课程中的效应为0.33,这表明相对于概率统计课程来说微积分课程中一班成绩明显优于二班成绩.

表4 两班微积分成绩统计
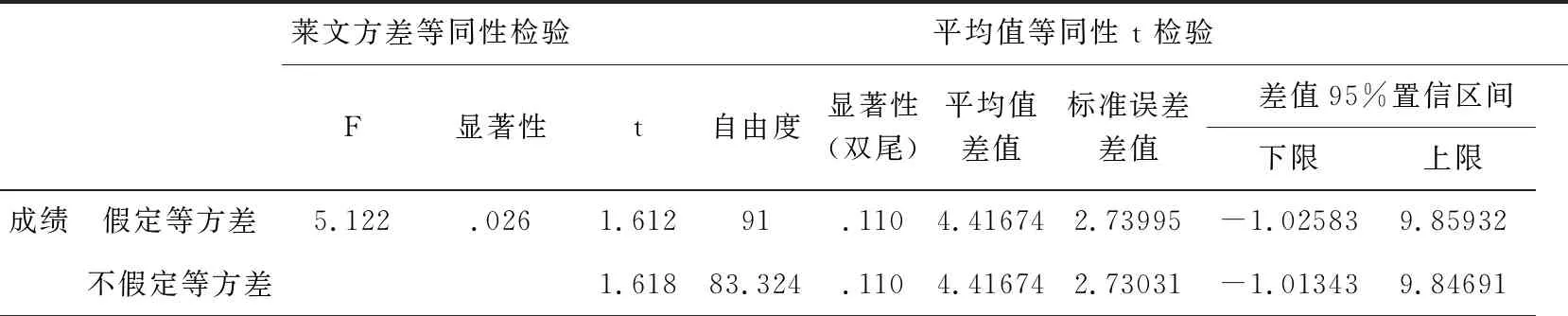
表5 两班微积分成绩的T检验
下面给出了近三年的学生评教分数(见表6). 2020年秋季这个学期也同时增加了学生的学习任务,这通常会造成评教分数降低,正是因为实施了课程思政,使得学生愿意接受学习任务,因而此学期的评教分数反而提高了.这里也附上2020年秋季班级的部分学生评教评语 (见表7),表明了学生对这种教学模式的认可.

表6 评教分数的变化

表7 学生评教
6 结 论
基于学习动机理论从不同角度构建大学数学中的课程思政,将课程思政融入到教学策略的实施上和教学内容的重塑上,在教学实践上取得了一定的成效.从学习动机层面来说,学习动机理论为课程思政的必要性提供支持,反过来,课程思政使得外部的激励逐步内化到学生的价值观中,又极大地促进了学习动机,这个内化过程正好符合自我决定动机理论.依托学习动机理论将课程思政内化到学生心中,促进学生认知发展和能力培养,即解决了专业教育和思政教育“两张皮”的问题,又将价值塑造、知识传授和能力培养三者融为一体.
课程思政和学习动机理论的内涵都十分丰富,本文也只是略涉皮毛,希望对课程思政的推进能起到抛砖引玉的作用.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

