一类时滞肿瘤-免疫模型的稳定性与分岔分析

周 琪， 王 珍

(合肥工业大学数学学院，合肥 230601)

1 引 言

免疫系统是机体执行免疫应答以及免疫功能的重要系统，进入机体的病原体大都会被免疫系统攻击消灭，但有些病毒会通过伪装躲避免疫系统的攻击，最终形成肿瘤.多年以来，免疫系统和肿瘤之间相互作用的模型已经得以建立和完善，参考文献[1]提出了一个五维微分方程组来描述效应细胞和免疫原性肿瘤间的相互作用，该系统可简化为下面的二维模型

(1)

其中E=E(t)和T=T(t)分别表示t时刻效应细胞和肿瘤细胞的浓度，σ表示肿瘤细胞从外部区域流入肿瘤部位的正常速率，Michlis-Menten函数cET/(g+T)描述肿瘤细胞对效应细胞的影响，c是作用速率，g为相关常数，β是效应细胞被肿瘤细胞破坏的速率，参数μ为效应细胞的自然死亡率.第2个方程中，假设在没有效应细胞的情况下，肿瘤细胞的增长是Logistic型增长，r是内禀增长率，K是环境容纳量，α为效应细胞杀死肿瘤细胞的速率.

参考文献[2]假设肿瘤对效应细胞的恶性潜能受质量作用规律的影响，由肿瘤的抗原性引起的效应细胞的增加与肿瘤细胞的浓度成正比，即cT，并用Michlis-Menten函数αET/(1+ρT)描述效应细胞对肿瘤细胞的影响，所以得到如下模型：

(2)

其中ρ为常数.作者研究了该模型的平衡点的存在性、平衡点的稳定性、系统的分岔情况等，并结合数值分析图像验证了理论结果.

肿瘤细胞接触效应细胞后作用是即时的，但效用是延迟的，即肿瘤细胞从接触效应细胞到破坏效应细胞之间存在时滞τ[3]，即t时刻被破坏的肿瘤细胞，实际上是被t-τ时刻与其接触的效应细胞破坏的.因此在模型(2)中的效应细胞中引入时滞τ，得到如下模型：

(3)

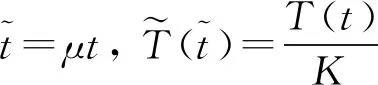
为了方便讨论，仍采用原来的符号，所以可得模型

(4)

此时滞微分方程(4)的初始条件为E(x)=φ1(x)，T(x)=φ2(x)，x∈[-τ，0]，其中φi(x)(i=1，2)在[-τ，0]上为连续非负函数.

关于这类模型，参考文献[4]和参考文献[5]等主要研究了不同类型捕食模型的平衡点的稳定性和Hopf分岔. 本文将讨论模型(4)的平衡点的存在性、稳定性及Hopf分岔.

2 解的非负性及平衡点的存在性

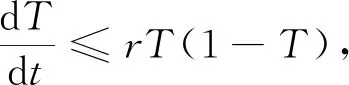
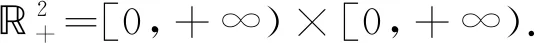
模型(4)的平衡点满足

(5)

令T=0，得边界平衡点(无肿瘤平衡点)P0(σ，0)，下面考虑模型(4)的正平衡点的存在性.

方程(5)中消除E可得下面关于T的方程

其中

f(T)=c3T3+c2T2+c1T+c0，

(6)

并且c3=βρ>0，c2=β+(1-β)ρ，c1=1-β+cα-ρ，c0=ασ-1.

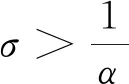
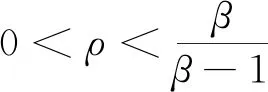
至此已经分析清楚了f(T)各个系数的符号变化，根据笛卡尔符号规则，可以确定f(T)的正根T的个数，最终结果归纳于表1中.由表1知除无肿瘤平衡点外，模型(4)最多有三个正平衡点，表格中的“-”和“+”分别表示ci小于零和大于零.

表1

3 平衡点的稳定性及Hopf分岔

模型(4)的无肿瘤平衡点为P0(σ，0)，可能存在的正平衡点记为Pk(Ek，Tk)(k=1，2，3).本节主要讨论了无肿瘤平衡点和正平衡点的局部稳定性及模型(4)的Hopf分岔情况.

3.1 P0的局部稳定性

在模型(4)中令x=E-E′，y=T-T′，则得模型(4)在任意平衡点P′(E′，T′)处的线性方程组

(7)

定理1对所有τ≥0，若ασ>1，则无肿瘤平衡点P0是局部渐近稳定的；若ασ<1，则P0是不稳定的.

证在无肿瘤平衡点P0(σ，0)处，方程(7)的特征方程为(λ+1)[λ-(r-rασ)]=0，则特征值为-1和r(1-ασ)，且均与τ无关.因此对任意τ≥0，当ασ>1时，P0是局部渐近稳定的，当ασ<1时，P0是不稳定的.

3.2 Pk的局部稳定性及Hopf分岔

在方程(7)中，令x(t)=C1eλt，y(t)=C2eλt(C1和C2为非负常数)，则方程(7)在正平衡点Pk(Ek，Tk) (k=1，2，3)处的特征方程为

H(λ)=λ2+a1λ+a2+a3e-λτ=0，

(8)

其中

定理2(i) 当τ=0时，模型(4)的正平衡点是稳定的当且仅当a1>0且a2+a3>0；

证(i) 当τ=0时，模型(4)的平衡点是局部渐近稳定的当且仅当方程H(λ)=λ2+a1λ+a2+a3=0的根均有负实部.根据Routh-Hurwitz判据[6]，H(λ)=0的根均有负实部当且仅当a1>0且a2+a3>0；

(ii) 令λ=iω(ω>0)为方程(8)的根，将其带入(8)式并分离实部和虚部，则有

(9)

将(9)中的两个等式两边同时平方、相加，并令ξ=ω2，则有

(10)

若

(11)

或

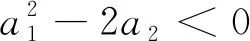
(12)

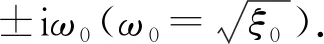
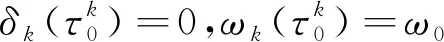
因此

4 数值分析

本节中将给出一个例子，并通过数值计算和模拟，验证定理2中证明的模型正平衡点附近的动力学行为.模型(4)中除时滞τ外，其它参数可取值为

β=3，ρ=6.6，c=7.4，α=1.6，σ=0.4，r=5.5，

(13)

经计算得

c3=19.8，c2=-10.2，c1=3.24，c0=-0.36.

由表1知方程(6)有一个或三个正根，经计算得唯一正平衡点P*(E*，T*)=(1.1101，0.1745)，并且

a1=0.0531，a2=3.0409，a3=-2.3768.

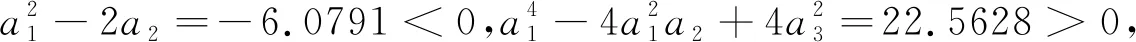
取τ=1.32∈[0，1.3277)，初值函数为(E，T)=(1.2，0.18)，图像(a)，(b)表明模型(4)中(E(t)，T(t))随着时间的增加，最终趋向于平衡点P*；由图(c)可以看出正平衡点P*是局部稳定的，是局部吸引子.

(a)，(b) τ=1.32时E和T的时间动态图 (c) 平衡点P*为局部吸引子

当τ=1.5∈(1.3277，+∞)，取初值函数为(E，T)=(0.5，0.15)，由图(d)，(e)知，方程(4)有周期解，P*是不稳定的；由图(f)知，平衡点P*外有一个稳定的极限环环绕.

(d)，(e) τ=1.5时E和T的时间动态图 (f) 平衡点P*外稳定的极限环

5 结 论

本文在参考文献[2]研究的基础上，在肿瘤-免疫模型(2)中引入了时滞，更符合实际情况，分析了改进后的模型的平衡点存在性、稳定性以及发生分岔的条件，并取一组参数进行数值模拟，以图象直观地验证理论的推导.基于本文的分析，在实际问题中可以通过控制参数的取值范围，来达到控制肿瘤细胞增长的目的.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.